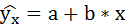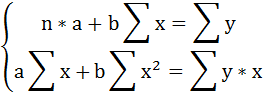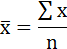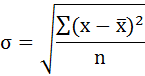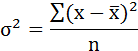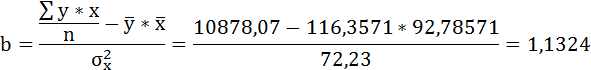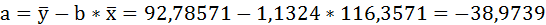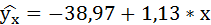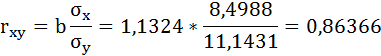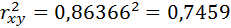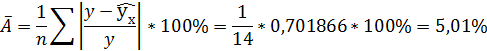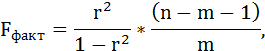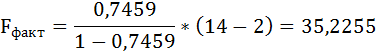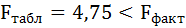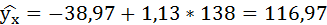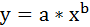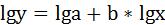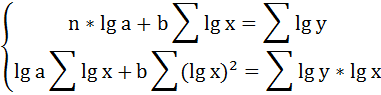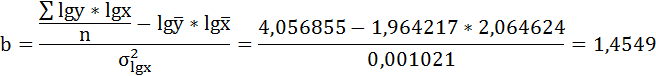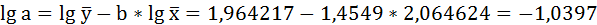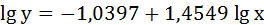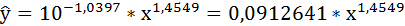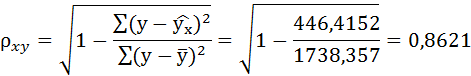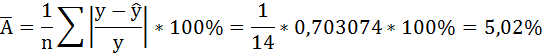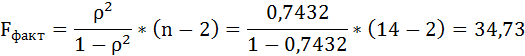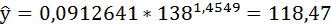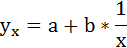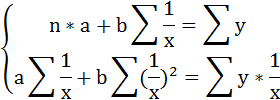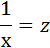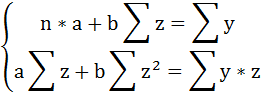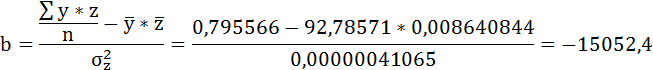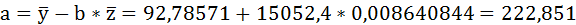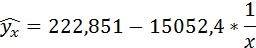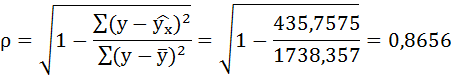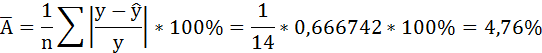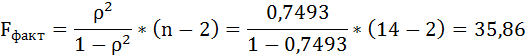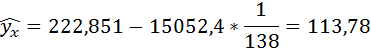Построить линейное уравнение связи между признаками

Построение линейной модели регрессии по данным эксперимента

п.1. Результативные и факторные признаки

Инвестиции в проект

Затраты на рекламу

По характеру зависимости признаков различают:

• Функциональную зависимость , когда каждому определенному значению факторного признака x соответствует одно и только одно значение результативного признака \(y=f(x)\).
• Статистическую зависимость , когда каждому определенному значению факторного признака x соответствует некоторое распределение \(F_Y(y|x)\) вероятностей значений результативного признака.

Например:
Функциональные зависимости: \(y(x)=x^2+3,\ S(R)=\pi R^2,\ V(a)=a^3\)
Статистические зависимости: средний балл успеваемости в зависимости от потраченного на учебу времени, рост в зависимости от возраста, количество осадков в зависимости от времени года и т.п.

Линейная модель парной регрессии

Например:
Прогноз погоды, автоматическая диагностика заболевания по результатам обследования, распознавание отпечатка на сканере и т.п.
В принципе, все сегодняшние компьютерные «чудеса» по поиску, обучению и распознаванию основаны на статистических моделях.

Рассмотрим саму простую модель: построение прямой \(Y=aX+b\) на основе полученных данных. Такая модель называется линейной моделью парной регрессии .

Пусть Y — случайная величина, значения которой требуется определить в зависимости от факторной переменной X.
Пусть в результате измерений двух случайных величин X и Y был получен набор точек \(\left\<(x_i;y_i)\right\>,\ x_i\in X,\ y_i\in Y\).
Пусть \(y*=y*(x)\) — оценка значений величины Y на данном наборе \(x_i\). Тогда для каждого значения x случайной величиной является ошибка оценки: $$ \varepsilon (x)=y*(x)-Y $$ Например, если полученный набор точек при размещении на графике имеет вид:

тогда разумно будет выдвинуть гипотезу, что для генеральной совокупности \(Y=aX+b\).
А для нашей выборки: \(y_i=ax_i+b+\varepsilon_i,\ i=\overline<1,k>\)
т.к., каждая точка выборки может немного отклоняться от прямой.

Наша задача: на данном наборе точек \(\left\<(x_i;y_i)\right\>\) найти параметры прямой a и b и построить эту прямую так, чтобы отклонения \(\varepsilon_i\) были как можно меньше.

п.3. Метод наименьших квадратов, вывод системы нормальных уравнений

Идея метода наименьших квадратов (МНК) состоит в том, чтобы найти такие значения a и b, для которых сумма квадратов всех отклонений \(\sum \varepsilon_i^2\rightarrow\ min\) будет минимальной.
Т.к. \(y_i=ax_i+b+\varepsilon_i\), сумма квадратов отклонений: $$ \sum_^k \varepsilon_i^2=\sum_^k (y_i-ax_i-b)^2\rightarrow min $$ Изучая производные, мы уже решали задачи на поиск экстремума (см. §50 данного справочника).
В данном случае нас интересует «двойной» экстремум, по двум переменным: $$ S(a,b)=\sum_^k (y_i-ax_i-b)^2 $$ Сначала берем производную по a, считая b постоянной, и приравниваем её к 0: \begin \frac<\partial S(a,b)><\partial a>=\frac<\partial><\partial a>\sum_^k (y_i-ax_i-b)^2=\sum_^k \frac<\partial><\partial a>(y_i-ax_i-b)^2=\\ =\sum_^k 2(y_i-ax_i-b)\cdot (-x_i)=-2\sum_^k x_i(y_i-ax_i-b)=0 \end Теперь то же самое делаем для b: \begin \frac<\partial S(a,b)><\partial b>=\frac<\partial><\partial b>\sum_^k (y_i-ax_i-b)^2=\sum_^k \frac<\partial><\partial b>(y_i-ax_i-b)^2=\\ =\sum_^k 2(y_i-ax_i-b)\cdot (-1)=-2\sum_^k (y_i-ax_i-b)=0 \end Получаем систему: \begin \begin \sum_^k x_i(y_i-ax_i-b)=0\\ \sum_^k (y_i-ax_i-b)=0 \end \\ \begin \sum_^k x_iy_i-a\sum_^k x_i^2-b\sum_^k x_i=0\\ \sum_^k y_i-a\sum_^k x_i-b\sum_^k 1=0 \end \end Переставим уравнения местами и запишем в удобном для решения виде.

Наши неизвестные – это a и b. И получена нами система двух линейных уравнений с двумя неизвестными, которую мы решаем методом Крамера (см. §48 справочника для 7 класса). \begin \triangle = \begin \sum_^k x_i & k\\ \sum_^k x_i^2 & \sum_^k x_i \end,\ \ \triangle_a = \begin \sum_^k y_i & k\\ \sum_^k x_iy_i & \sum_^k x_i \end,\ \ \triangle_b = \begin \sum_^k x_i & \sum_^k y_i\\ \sum_^k x_i^2 & \sum_^k x_iy_i \end \\ a=\frac<\triangle_a><\triangle>,\ \ b=\frac<\triangle_b> <\triangle>\end
Например:
Найдем и построим прямую регрессии для набора точек, представленных на графике выше. Общее число точек k=10.
Расчетная таблица:

Получаем: \begin \sum_^k x_i=22,2;\ \sum_^k x_i^2=71,25;\ \sum_^k x_iy_i=169,475;\ \sum_^k y_i=61,95\\ \triangle = \begin 22,2 & 10\\ 71,25 & 22,2 \end=22,2^2-10\cdot 71,25=-206,25\\ \triangle_a = \begin 61,95 & 10\\ 169,475 & 22,2 \end=61,95\cdot 22,2-10\cdot 169,475=-300,875\\ \triangle_b = \begin 22,2 & 61,95\\ 71,25 & 169,475 \end=22,2\cdot 169,475-61,95\cdot 71,25=-600,75 \\ a=\frac<\triangle_a><\triangle>=\frac<-300,875><-206,25>\approx 1,46,\ \ b=\frac<\triangle_b><\triangle>=\frac<-600,75><-206,25>\approx 2,91 \end

п.4. Оценка тесноты связи

Найденное уравнение регрессии всегда дополняют расчетом показателя тесноты связи.
Введем следующие средние величины: $$ \overline=\frac1k\sum_^k x_i,\ \ \overline=\frac1k\sum_^k y_i,\ \ \overline=\frac1k\sum_^k x_i^2,\ \ \overline=\frac1k\sum_^k y_i^2,\ \ \overline=\frac1k\sum_^k x_iy_i $$ Дисперсия каждой из случайных величин x и y: $$ D_x=\overline-(\overline)^2,\ \ D_y=\overline-(\overline)^2 $$ СКО каждой из случайных величин: $$ \sigma_x=\sqrt<\overline-(\overline)^2>,\ \ \sigma_y=\sqrt<\overline-(\overline)^2>,\ \ $$

Значения линейного коэффициента корреляции находится в интервале $$ -1\leq r_\leq 1 $$ Чем ближе \(|r_|\) к единице, тем сильнее линейная связь между x и y.
Отрицательные значения \(|r_|\) соответствуют обратной связи: убывающей прямой с отрицательным угловым коэффициентом.

Для оценки тесноты связи на практике пользуются шкалой Чеддока :

Задача №1 Построение уравнения регрессии

Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).

Требуется:

1. Для характеристики зависимости у от х рассчитать параметры следующих функций:

В) равносторонней гиперболы.

2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.

Решение:

1. Для расчёта параметров линейной регрессии

Решаем систему нормальных уравнений относительно a и b:

Построим таблицу расчётных данных, как показано в таблице 1.

Таблица 1 Расчетные данные для оценки линейной регрессии

№ п/п	х	у	ху	x 2	y 2
1	100	70	7000	10000	4900	74,26340	0,060906
2	105	79	8295	11025	6241	79,92527	0,011712
3	108	85	9180	11664	7225	83,32238	0,019737
4	113	84	9492	12769	7056	88,98425	0,059336
5	118	85	10030	13924	7225	94,64611	0,113484
6	118	85	10030	13924	7225	94,64611	0,113484
7	110	96	10560	12100	9216	85,58713	0,108467
8	115	99	11385	13225	9801	91,24900	0,078293
9	119	100	11900	14161	10000	95,77849	0,042215
10	118	98	11564	13924	9604	94,64611	0,034223
11	120	99	11880	14400	9801	96,91086	0,021102
12	124	102	12648	15376	10404	101,4404	0,005487
13	129	105	13545	16641	11025	107,1022	0,020021
14	132	112	14784	17424	12544	110,4993	0,013399
Итого:	1629	1299	152293	190557	122267	1299,001	0,701866
Среднее значение:	116,3571	92,78571	10878,07	13611,21	8733,357	х	х
	8,4988	11,1431	х	х	х	х	х
	72,23	124,17	х	х	х	х	х

Среднее значение определим по формуле:

Cреднее квадратическое отклонение рассчитаем по формуле:

и занесём полученный результат в таблицу 1.

Возведя в квадрат полученное значение получим дисперсию:

Параметры уравнения можно определить также и по формулам:

Таким образом, уравнение регрессии:

Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.

Рассчитаем линейный коэффициент парной корреляции:

Связь прямая, достаточно тесная.

Определим коэффициент детерминации:

Вариация результата на 74,59% объясняется вариацией фактора х.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .

,

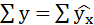
следовательно, параметры уравнения определены правильно.

Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:

В среднем расчётные значения отклоняются от фактических на 5,01%.

Оценку качества уравнения регрессии проведём с помощью F-теста.

F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

F_факт определяется по формуле:

где n – число единиц совокупности;

m – число параметров при переменных х.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза.

Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

2. Степенная регрессия имеет вид:

Для определения параметров производят логарифмиро­вание степенной функции:

Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наи­меньших квадратов:

Построим таблицу расчётных данных, как показано в таблице 2.

Таблица 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у	lg x	lg y	lg x*lg y	(lg x) 2	(lg y) 2
1	100	70	2,000000	1,845098	3,690196	4,000000	3,404387
2	105	79	2,021189	1,897627	3,835464	4,085206	3,600989
3	108	85	2,033424	1,929419	3,923326	4,134812	3,722657
4	113	84	2,053078	1,924279	3,950696	4,215131	3,702851
5	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
6	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
7	110	96	2,041393	1,982271	4,046594	4,167284	3,929399
8	115	99	2,060698	1,995635	4,112401	4,246476	3,982560
9	119	100	2,075547	2,000000	4,151094	4,307895	4,000000
10	118	98	2,071882	1,991226	4,125585	4,292695	3,964981
11	120	99	2,079181	1,995635	4,149287	4,322995	3,982560
12	124	102	2,093422	2,008600	4,204847	4,382414	4,034475
13	129	105	2,110590	2,021189	4,265901	4,454589	4,085206
14	132	112	2,120574	2,049218	4,345518	4,496834	4,199295
Итого	1629	1299	28,90474	27,49904	56,79597	59,69172	54,05467
Среднее значение	116,3571	92,78571	2,064624	1,964217	4,056855	4,263694	3,861048
	8,4988	11,1431	0,031945	0,053853	х	х	х
	72,23	124,17	0,001021	0,0029	х	х	х

Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у
1	100	70	74,16448	17,34292	0,059493	519,1886
2	105	79	79,62057	0,385112	0,007855	190,0458
3	108	85	82,95180	4,195133	0,024096	60,61728
4	113	84	88,59768	21,13866	0,054734	77,1887
5	118	85	94,35840	87,57961	0,110099	60,61728
6	118	85	94,35840	87,57961	0,110099	60,61728
7	110	96	85,19619	116,7223	0,11254	10,33166
8	115	99	90,88834	65,79901	0,081936	38,6174
9	119	100	95,52408	20,03384	0,044759	52,04598
10	118	98	94,35840	13,26127	0,037159	27,18882
11	120	99	96,69423	5,316563	0,023291	38,6174
12	124	102	101,4191	0,337467	0,005695	84,90314
13	129	105	107,4232	5,872099	0,023078	149,1889
14	132	112	111,0772	0,85163	0,00824	369,1889
Итого	1629	1299	1296,632	446,4152	0,703074	1738,357
Среднее значение	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Решая систему нормальных уравнений, определяем параметры логарифмической функции.

Получим линейное уравнение:

Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 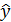. По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 5,02%.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

3. Уравнение равносторонней гиперболы

Для определения параметров этого уравнения используется система нормальных уравнений:

Произведем замену переменных

и получим следующую систему нормальных уравнений:

Решая систему нормальных уравнений, определяем параметры гиперболы.

Составим таблицу расчётных данных, как показано в таблице 3.

Таблица 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у	z	yz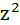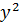
1	100	70	0,010000000	0,700000	0,0001000	4900
2	105	79	0,009523810	0,752381	0,0000907	6241
3	108	85	0,009259259	0,787037	0,0000857	7225
4	113	84	0,008849558	0,743363	0,0000783	7056
5	118	85	0,008474576	0,720339	0,0000718	7225
6	118	85	0,008474576	0,720339	0,0000718	7225
7	110	96	0,009090909	0,872727	0,0000826	9216
8	115	99	0,008695652	0,860870	0,0000756	9801
9	119	100	0,008403361	0,840336	0,0000706	10000
10	118	98	0,008474576	0,830508	0,0000718	9604
11	120	99	0,008333333	0,825000	0,0000694	9801
12	124	102	0,008064516	0,822581	0,0000650	10404
13	129	105	0,007751938	0,813953	0,0000601	11025
14	132	112	0,007575758	0,848485	0,0000574	12544
Итого:	1629	1299	0,120971823	11,13792	0,0010510	122267
Среднее значение:	116,3571	92,78571	0,008640844	0,795566	0,0000751	8733,357
	8,4988	11,1431	0,000640820	х	х	х
	72,23	124,17	0,000000411	х	х	х

Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у
1	100	70	72,3262	0,033231	5,411206	519,1886
2	105	79	79,49405	0,006254	0,244083	190,0458
3	108	85	83,47619	0,017927	2,322012	60,61728
4	113	84	89,64321	0,067181	31,84585	77,1887
5	118	85	95,28761	0,121031	105,8349	60,61728
6	118	85	95,28761	0,121031	105,8349	60,61728
7	110	96	86,01027	0,10406	99,79465	10,33166
8	115	99	91,95987	0,071112	49,56344	38,6174
9	119	100	96,35957	0,036404	13,25272	52,04598
10	118	98	95,28761	0,027677	7,357059	27,18882
11	120	99	97,41367	0,016024	2,516453	38,6174
12	124	102	101,46	0,005294	0,291565	84,90314
13	129	105	106,1651	0,011096	1,357478	149,1889
14	132	112	108,8171	0,028419	10,1311	369,1889
Итого:	1629	1299	1298,988	0,666742	435,7575	1738,357
Среднее значение:	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Значения параметров регрессии a и b составили:

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 4,76%.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.

Основы корреляционного анализа. Примеры анализа прямолинейной связи при парной корреляции

Исследование объективно существующих связей между явлениями — важнейшая задача статистики. В процессе статистического исследования зависимостей выявляются причинно-следственные отношения между явлениями. Причинно-следственные отношения — это такая связь явлений и процессов, когда изменение одного из них — причины ведет к изменению другого — следствия.

Признаки явлений и процессов по их значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других, связанных с ними признаков, называют факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, называют результативными.

В статистике различают функциональные и стохастические (вероятностные) связи явлений и процессов:

• Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно значение результативного.
• Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической (вероятностной). Частным случаем стохастической связи является корреляционная связь.

Кроме того, связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению.

По направлению выделяют связь прямую и обратную:

• Прямая связь — это такая связь, при которой с увеличением (уменьшением) значений факторного признака происходит увеличение (уменьшение) значений результативного. Так, например, рост производительности труда способствует увеличению уровня рентабельности производства.
• В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака. Так с увеличением уровня фондоотдачи снижается себестоимость единицы производимой продукции.

По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные:

• Если статистическая связь между явлениями может быть приблизительно выражена уравнением прямой линии, то ее называют линейной связью вида: у=а+bх.
• Если же связь может быть выражена уравнением какой-либо кривой линии (параболы, гиперболы и др.), то такую связь называют нелинейной (криволинейной) связью.

Теснота связи показывает меру влияния факторного признака на общую вариацию результативного признака. Классификация связи по степени тесноты представлена в таблице 1.

Для выявления наличия связи, ее характера и направления в статистике используются следующие методы: приведения параллельных данных, аналитических группировок, графический, корреляции. Основным методом изучения статистической взаимосвязи является статистическое моделирование связи на основе корреляционного и регрессионного анализа.

Корреляция — это статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. В статистике принято различать следующие виды корреляции:

• парная корреляция — связь между двумя признаками (результативным и факторным, или двумя факторными);
• частная корреляция — зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;
• множественная корреляция — зависимость результативного и двух или более факторных признаков, включенных в исследование.

Задачей корреляционного анализа является количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).

Теснота связи количественно выражается величиной коэффициентов корреляции, которые давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии.

Корреляция взаимосвязана с регрессией, поскольку первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму.

Регрессионный анализ заключается в определении аналитического выражения связи в виде уравнения регрессии.

Регрессией называется зависимость среднего значения случайной величины результативного признака от величины факторного, а уравнением регрессии – уравнение описывающее корреляционную зависимость между результативным признаком и одним или несколькими факторными.

Формулы корреляционно-регрессионного анализа для прямолинейной связи при парной корреляции представлены в таблице 2.

Показатель	Обозначение и формула
Уравнение прямой при парной корреляции	yx = a +bx, где b — коэффициент регрессии
Система нормальных уравнений способом наименьших квадратов для определения коэффициентов a и b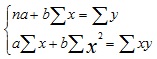
Линейный коэффициент корреляции для определения тесноты связи, его интерпретация: r = 0 – связь отсутствует; 0 2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна источники: http://ecson.ru/economics/econometrics/zadacha-1.postroenie-regressii-raschyot-korrelyatsii-oshibki-approximatsii-otsenka-znachimosti-i-prognoz.html http://www.ekonomika-st.ru/drugie/metodi/metodi-statistika-1-8.html Вам также может понравиться Оксид кальция получение карбонат кальция уравнение Карбонат кальция: способы получения и химические свойства Карбонат кальция CaCO3 — соль кальция и угольной кислоты. Уравнение электрической диссоциации сульфата никеля Гидролиз сульфата никеля (II) NiSO4 — соль образованная слабым основанием и сильной кислотой, поэтому 2no o2 2no2 ионное уравнение 2no o2 2no2 ионное уравнение Вопрос по химии: Составьте полное и краткое ионное уравнение 2NO+O2=2NO2+Q Пропан горит согласно уравнению реакции Пропан горит согласно уравнению реакции: C3H8 + 5O5 -> 3CO2+4H2O Определите объем кислорода (н.