Построить разностную схему для уравнения

О построении разностных схем

Как уже отмечалось, построение разностных схем решения уравнений с частными производными основано на введении сетки в рассматриваемом пространстве. Узлы сетки являются расчетными точками.

Пример простейшей прямоугольной области G(z, у) с границей Г в двумерном случае показан на рис. 2.1. Стороны прямоугольника делятся на элементарные отрезки точками и . Через эти точки проводятся два семейства координатных прямых х = const и у = const, образующих сетку с прямоугольными ячейками. Любой ее узел, номер которого (i,j), определяется координатами (xi, yj). Поскольку все ячейки показанной на рис. 2.1 сетки одинаковы, такую сетку называют равномерной сеткой.

Рис. 2.1. Прямоугольная сетка

Аналогично вводятся сетки для многомерных областей, содержащих более двух измерений. На рис. 2.2 показан элемент сетки в виде прямоугольного параллелепипеда для трехмерной области.

Рис. 2.2. Элемент сетки

Прямоугольные сетки наиболее удобны при организации вычислительного алгоритма. Вместе с тем, некоторые схемы используют сетки с ячейками более сложной формы: треугольными, четырехугольными (не прямоугольными), шестиугольными и т.д.

Узлы сетки, лежащие на границе Г области G, называются граничными узлами. Все остальные узлы — внутренними. Поскольку начальные и граничные условия при постановке задач формулируются на границе расчетной области, то их можно считать заданными в граничных узлах сетки. Иногда граничные точки области не являются узлами сетки, что характерно для областей сложной формы. Тогда либо вводят дополнительные узлы на пересечении координатных линий с границей, либо границу приближенно заменяют ломаной, проходящей через близкие к границе узлы. На эту ломаную переносятся граничные условия.

В ряде случаев сложные криволинейные области с помощью перехода к новым независимым переменным удается свести к простейшему виду. Например, четырехугольную область G, изображенную на рис. 2.3, можно привести к единичному квадрату G‘ введением новых переменных вместо х, у с помощью соотношений

Рис. 2.3. Преобразование расчетной области

К новым переменным нужно преобразовать уравнения, а также начальные и граничные условия.

Вобласти G‘ можно ввести прямоугольную сетку, при этом в области Gей будет соответствовать сетка с неравномерно расположенными узлами и криволинейными ячейками.

В дальнейшем при построении разностных схем мы для простоты будем использовать прямоугольные сетки (или с ячейками в виде прямоугольных параллелепипедов в трехмерном случае), а уравнения будем записывать в декартовых координатах (х, у, z). На практике приходится решать задачи в различных криволинейных системах координат: полярной, цилиндрической, сферической и др. Например, если расчетную область удобно задать в полярных координатах (r,φ), то в ней сетка вводится с шагами и , соответственно, по радиус-вектору и полярному углу.

Иногда и в простой расчетной области вводят неравномерную сетку. В частности, в ряде случаев необходимо проводить сгущение узлов для более точного расчета в некоторых частях рассматриваемой области. При этом области сгущения узлов либо известны заранее, либо определяются в процессе решения задачи (например, в зависимости от градиентов искомых функций). В последнем случае получающиеся сетки называют адаптивными.

Для построения разностной схемы, как и в случае обыкновенных дифференциальных уравнений, частные производные в уравнении заменяются конечно-разностными соотношениями по некоторому шаблону. При этом точные значения искомой функции заменяются значениями сеточной функции в узлах разностной сетки.

В качестве примера построим некоторые разностные схемы для решения уравнения теплопроводности при заданных начальных и граничных условиях. Запишем смешанную краевую задачу в виде

(2.2)

где — начальное распределение температуры U(при t= 0); , — распределение температуры на концах рассматриваемого отрезка (х = 0, 1) в любой момент времени t. Заметим, что начальные и граничные условия должны быть согласованы, т.е. .

Введем равномерную прямоугольную сетку с помощью координатных линий , ; hи τ — соответственно шаги сетки по направлениям х и t. Значения функции в узлах сетки обозначим . Эти значения заменим соответствующими значениями сеточной функции , которые удовлетворяют уравнениям, образующим разностную схему. Часто верхний индекс заключают в скобки, чтобы не путать его с показателем степени. Здесь и далее скобки для краткости опушены.

Заменяя в исходном уравнении (2.2) частные производные искомой функции с помощью отношений конечных разностей, получаем разностную схему

. (2.3)

В записи этой схемы для каждого узла использован шаблон, изображенный на рис. 2.4, а.

Для одного и того же уравнения можно построить различные разностные схемы. В частности, если воспользоваться шаблоном, изображенным на рис. 2.4, б,т.е. аппроксимировать производную при :

,

то вместо (2.3) получим разностную схему

(2.4)

И в том и другом случае получается система алгебраических уравнений для определения значений сеточной функции во внутренних узлах. Значения в граничных узлах находятся из граничных условий:

(2.5)

Совокупность узлов при t = const, т. е. при фиксированном значении j, называется слоем (или, поскольку переменная tсоответствует времени, временным слоем).Схема (2.3) позволяет последовательно находить значения на -ом слое через соответствующие значения на j-ом слое. Такие схемы называются явными.

Для начала счета по схеме (2.3) при j= 1 необходимо знать решение на начальном слое при j= 0. Оно определяется начальным условием (2.2), которое запишется в виде:

(2.6)

В отличие от явной схемы каждое разностное уравнение (2.4) содержит на каждом новом слое три неизвестных значения: поэтому нельзя сразу определить эти значения через известное решение на предыдущем слое. Такие схемы называются неявными.При этом разностная схема (2.4) состоит из линейных трехточечных уравнений, т.е. каждое уравнение содержит неизвестную функцию в трех точках данного слоя. Такие системы линейных уравнений с трехдиагональной матрицей могут быть решены методом прогонки, в результате чего будут найдены значения сеточной функции в узлах.

Заметим, что в рассмотренном примере мы получаем двухслойные схемы,когда в каждое разностное уравнение входят значения функции из двух слоев: нижнего, на котором решение уже найдено, и верхнего, в узлах которого решение ищется.

Спомощью рассматриваемого способа построения разностных схем, когда входящие в уравнение отдельные частные производные заменяются конечно-разностными соотношениями для сеточной функции (или сеточными выражениями), могут быть созданы многослойные схемы, а также схемы высоких порядков точности.

Несмотря на то, что этот способ получения разностных уравнений наиболее прост и поэтому широко используется при разработке численных методов, существуют также другие способы построения разностных схем. Изложение этих вопросов читатель может найти в более полных работах по численным методам и теории разностных схем.

Методы составления разностных схем

Лекция №9

Уравнения в частных производных

Введение

В физике, химии, биологии, социологии потребность в уравнениях в частных производных возникает при попытке описать динамику большого числа более или менее одинаковых дискретных объектов, входящих в некоторую системную целостность. Если количество таких дискретных объектом мало, то можно обойтись системой дифференциальных уравнений, в которой каждый дискретный объект описывается своей подсистемой обыкновенных дифференциальных уравнений.

В качестве примера можно привести модель хищник-жертва в математической биологии, когда хищник и жертва способны активно передвигаться, подобно тому, как передвигаются в водной среде планктонные организмы. Активное движение предполагает преследование хищником своей жертвы и, наоборот, убегание хищника от жертвы. В данном контексте оказалось возможным не только моделировать движение отдельных особей, но и описать динамику популяцию в целом. Поскольку количество планктона в океане это миллионы тонн, постольку описание предполагается в терминах плотностей биомасс отдельных видов. Следуя[1], можно привести следующие уравнения, описывающие динамику в пространстве и времени пары видов: одного вида хищника и одного вида жертвы:

(1)

где l₁, l₂ — параметры описывающие силы преследования и убегания, D₁, D₂ — коэффициенты диффузии, F₁, F₂ — члены ответственные за размножение жертвы, ее выедание хищником, и естественную смерть хищника.

Система уравнений (1) выведена из так называемого гидродинамического приближения, когда сообщество планктонных организмов рассматривается как сплошная среда. В качестве примера приведем уравнения, описывающие динамику вязкой несжимаемой жидкости:

(2)

где — поле скорости, — поле давления, r — плотность жидкости, m — кинематическая вязкость.

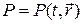
Наконец, приведем еще один пример уравнения теплопроводности, которое возникает в моделях сплошной среды для описания баланса тепла:

, (3)

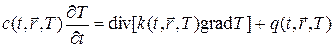
где — поле температуры, c — теплоемкость, k — коэффициент теплопроводности, q — плотность источников и стоков тепла.

К уравнениям в частных производных приводят задачи газовой динамики, гидродинамики, переноса излучения, теории упругости, описания электромагнитных полей, популяционной динамики, морфогенеза, математической экономики и во многих других задачах.

Из примеров (1) — (3) видно, что обычно в качестве независимых переменных выступает время t и пространство , но могут быть и другие независимые переменные. Обычно решение ищется в некоторой области изменения независимых переменных . Для выделения единственного решения из некоторого семейства решений задают некоторые дополнительные условия, обычно формулируемые на границе области.

При изучении процессов во времени нас обычно интересуют решения на отрезке времени [t₀,t₁], при этом область изменения независимых переменных может быть преобразована к виду:

. (4)

Согласно (4), решение определяется в области на отрезке времени [t₀,t₁], причем дополнительное условие, заданное при t = t₀ называется начальными данными, а на границе области — граничными или краевыми условиями.

Если в задаче определены только начальные данные, то ее называют задачей Коши. Так, для уравнения теплопроводности (3) в неограниченном пространстве можно сформулировать задачу с начальными данными

. (5)

Известно, что если — кусочно-непрерывная ограниченная функция, то решение задачи (3), (5) единственно в классе ограниченных функций.

Задачу с начальными и граничными условиями называют смешанной краевой задачей или нестационарной краевой задачей. Для смешаной задачи (3) дополнительные условия могут иметь, например, следующий вид:

. (6)

Часто постановка тех или иных физических задач приводит к ситуации, когда переходные процессы уже произошли и дальнейшая динамика отсутствует, т.е. зависимые переменные соответствующих уравнений не зависят от времени или являются стационарными. В этом случае задача формулируется в области , а дополнительные условия сводятся к краевым условиям на границе области .

Напомним известную классификацию уравнений в частных производных на примере одного уравнения, зависящего от двух переменных

. (7)

Если коэффициенты уравнения (7) не зависят от u, то уравнение является линейным, если коэффициенты являются константами — линейным уравнением с постоянными коэффициентами, если коэффициенты зависят от u, то уравнение (7) называется квазилинейным. Если A º B º C º 0. а D ¹ 0 и E ¹ 0, то уравнение (7) называется уравнением переноса и имеет первый порядок. Для уравнения второго порядка классификация определяется знаком дискриминанта B 2 — AC. Для гиперболических уравнений дискриминант положителен, для параболических — равен нулю, для эллиптических уравнений — отрицателен.

Точные методы решения

В курсе уравнений математической физики[2] изложен ряд методов нахождения точных решений. К ним относятся метод распространения волн, метод разделения переменных, метод функции Грина или источника.

Например, для простейшей задачи теплопроводности:

(8)

методом разделения переменных можно найти точное решение в виде бесконечной суммы

(9)

где соответствующие коэффициенты Фурье от начальных данных находятся в соответствии с формулой

. (10)

Решение задачи (8) — (10) проиллюстрируем на конкретном примере, код программы для которого приведен на листинге_№1.

%Изображение аналитического решения уравнения

%теплопроводности, представленного в виде

%конечного отрезка бесконечного ряда

%очищаем рабочее пространство

%определяем коэффициент теплопроводности и

%длину отрезка интегрирования

%определяем константы начального распределения

%температуры T0(x)=px, 0 0.5*a

%рисуем начальный температурный профиль

%организуем цикл вычисления значений температуры

%в различные моменты времени и изображение их на

На рис.1 приведен итог работы кода программы листинга_№1. Из графика видно, как начальные неоднородности, намеренно выбранные в виде острого кусочно-непрерывного профиля, со временем становятся гладкими линиями.

Подставляя (10) в (9) и меняя местами знаки интегрирование и суммирования, находим выражение для решения исходной задачи в терминах функции Грина

, (11)

где функция источника (Грина) равна

. (12)

Рис.1. Решение задачи (8) — (10)

Функция Грина для задачи Коши на всей оси имеет наиболее простой вид

. (12¢)

Функции влияния, подобные (12), (12¢) позволяют связать начальные данные с решением и сделать ряд важных замечаний о решениях в целом. Так, если начальное распределение сосредоточено на некотором отрезке [a,b], т.е. T₀(x) > 0 при x Î [a,b] и T₀(x) = 0, когда x Ï [a,b], то, согласно (11), (12¢), при t > 0 решение будет отличным от нуля в любой точке бесконечной оси. Это можно истолковать как то, что скорость распространения тепла в уравнении с линейной теплопроводностью бесконечна. Для сравнения с нелинейной теплопроводностью сошлемся на модель №5 в лекции №1. В этой модели рассматривалась ситуация остановки на некоторое время фронта тепловой волны.

Автомодельные решения

Уравнения в частных производных допускают классы упрощенных решений, которые получили название автомодельных. Для решений этого класса характерна зависимость функции решения от одной переменной x, которая является специальной комбинацией t, x.

Для построения примера автомодельного решения рассмотрим одномерное квазилинейное уравнение теплопроводности, в котором коэффициент теплопроводности степенным образом зависит от температуры, т.е.

, (13)

где k₀, s — некоторые неотрицательные константы. Зависимости степенного типа, подобные (13), весьма распространены в физики. Так, в физике плазмы известно, что коэффициент электронной теплопроводности пропорционален .

Построим автомодельное решение для уравнения (13) типа бегущей волны:

. (14)

Подставляя (14) в (13), приходим к следующему обыкновенному дифференциальному уравнению:

. (15)

Уравнение (15) можно один раз проинтегрировать. Появится константа, которую определим, предполагая, что бегущая волна двигается по нулевому температурному фону. После этих предположений возможно провести еще одно интегрирование и в окончательном виде получить:

(16)

Возвращаясь в (16) к представлению в координатах t, x, получим

(17)

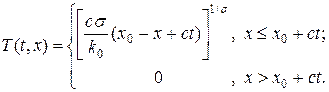
Автомодельное решение (17) представляет собой температурную волну, бегущую с постоянной скоростью по нулевому температурному фону. Фронт волны имеет координату x₀ + ct. Профили волны всюду гладкий, кроме фронта волны, где производная терпит разрыв.

На листинге_№2 приведен код программы, изображающей движение бегущей волны (17).

%Программа изображения бегущей волны квазилинейного

%очищаем рабочее пространство

%константы уравнения теплопроводности и бегущей волны

k0=1; sigma=3; c=4; x0=0.5;

%определяем сетки по времени и пространству

%организуем цикл рисования профиля температуры в

%различные моменты времени

%определяем профиль температуры

%рисуем начальный профиль температуры

%толстой красной линией

%вычисляем коэффициенты прогонки A(n), B(n)