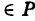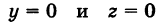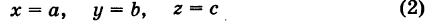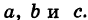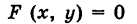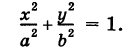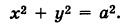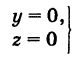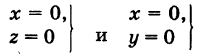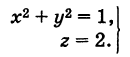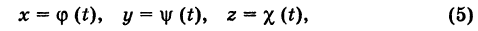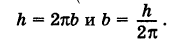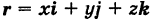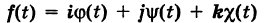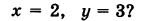Уравнения поверхности и линии в пространстве с примерами решения
Содержание:
Уравнения поверхности и линии в пространстве
Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если
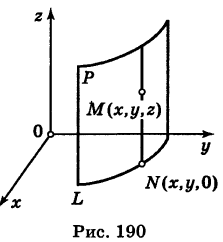
— уравнение поверхности Р (рис. 189), то при М(х, у, z)
Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.
Пример (уравнения координатных плоскостей):
Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,
— уравнение координатной плоскости Oyz. Аналогично,
— соответственно уравнения координатных плоскостей Oxz и Оху.
Формула 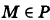
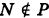
В более общем случае
— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные
Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.
Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 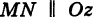
Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).
— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,
является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.
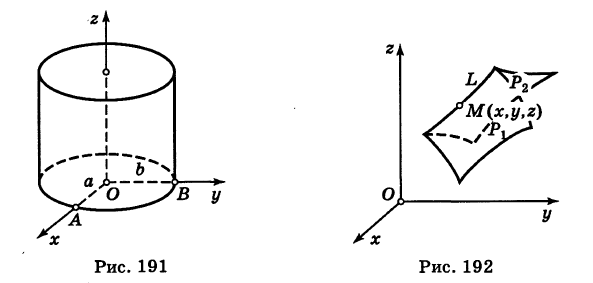
Пример (уравнение эллиптического цилиндра):
Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение
В частности, при а = b получаем уравнение кругового цилиндра
Линию L в пространстве можно задать как пересечение двух данных поверхностей 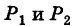

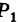
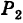
Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:
являющихся уравнениями поверхностей, определяющих данную линию.
Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки 
Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.
Определение: Уравнениями линии в пространстве 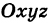
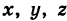
Пример (уравнения координатных осей):
Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому
— уравнения оси Ох. Аналогично,
— уравнения осей Оу и Oz соответственно.
Пример:
Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).
Решение:
Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть
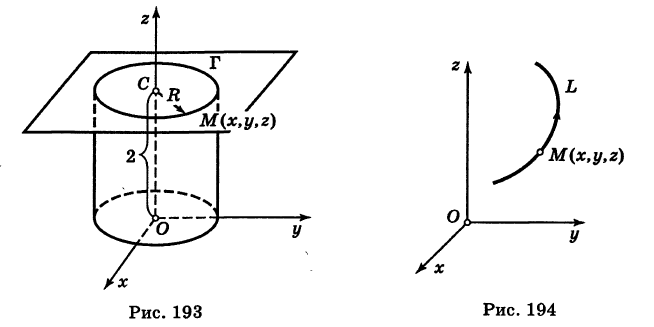
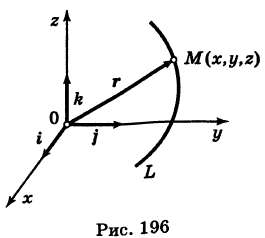
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем
где 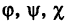
Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.
Пример:
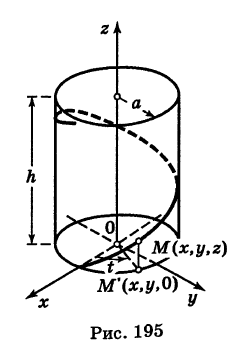
Написать уравнения винтовой линии радиуса а и шага 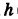
Решение:
Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.
Приняв за параметр 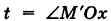
Для определения коэффициента пропорциональности b положим 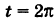
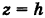
Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости 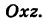
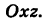
Текущую точку 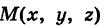
( 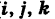
— так называемая вектор-функция скалярного аргумента t.
В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).
Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).
Пример:
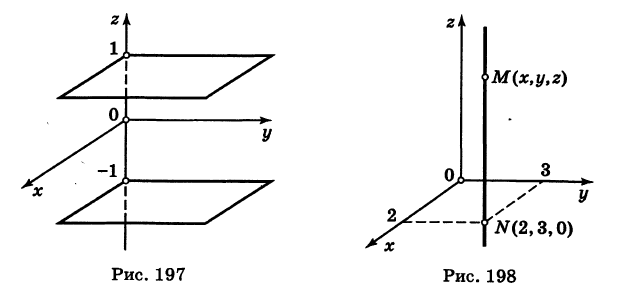
Какой геометрический образ соответствует уравнению
Решение:
Из уравнения (8) получаем 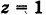
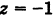
Пример:
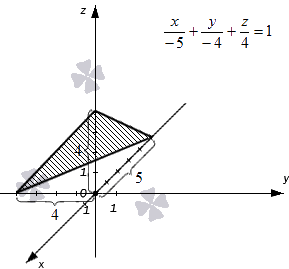
Какой геометрический образ соответствует паре уравнений
Решение:
Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Общее уравнение плоскости
- Угол между плоскостями
- Понятие о производной вектор-функции
- Криволинейные интегралы
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
- Полярные координаты
- Непрерывность функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Уравнение плоскости, виды уравнения плоскости
В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.
Определение уравнения плоскости
Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.
Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.
Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.
Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.
Общее уравнение плоскости
Сформулируем теорему, а затем запишем уравнение плоскости.
Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве
Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.
Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.
Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.
Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .
Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.
Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.
Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .
Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.
Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.
Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.
Нормальное уравнение плоскости
Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .
Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.
n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1
То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.
Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.
Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.
Уравнение плоскости в отрезках
Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.
Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .
Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.
Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .
Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.
Различные виды уравнений плоскости в пространстве



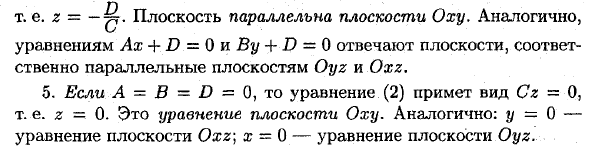


Различные виды уравнений плоскости в пространстве
- РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЙ ПЛОСКОСТИ В ПРОСТРАНСТВЕ Простейшая поверхность является плоскость. Плоскость в пространстве Oxijz можно задать разные способы. Каждая из них соответствует определенному виду ее уравнение. 1. Уравнение плоскости, проходящей через точку точки перпендикулярно существующего вектору Пусть в пространстве Oxyz плоскость Q задана точкой Mq
Выведем уравнение плоскости Q. При любом расположении точки М на плоскости Q векторы п и ДМК взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: п • ДМК = 0, т е , А (х-®0) + В (у-у0) + С (z-z0) = 0. (1) Координаты любой точки плоскости Q удовлетворяют (1), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них п • Л / о М ф 0).
Уравнение (1) называется уравнением плоскости, проходящей через данную точку Mq (хо \ уо; ZQ) .перпендикулярно вектору п =. (Л; В; С) Оно первой степени относительно текущих координат ху у и г. Вектор п — (А \ В \ С) называется нормальным вектором плоскости. .. Придавая коэффициентам А, В и С уравнения (1) различные значения, можно получить уравнение любой плоскости, проходящей через точку Mq Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей а уравнение (1) — уравнением связки плоскостей.
Рассмотрим общее уравнение первой степени с тремя переменными х, у vi z: (2) Ax + By + Cz + D = 0. Не равны нулю, например, В и 0, пеме (3) Сравнивал уравнение (3) с уравнением (1), видим, что уравнения (2) и (3) являются уравнением плоскости с нормальным вектором п = (А; В) С), проходящей через точку М \ (0; — Q; 0 ). Итак, уравнение (2) определяет в системе координат Oxyz некоторую плоскость.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Частные случаи общего уравнения плоскости: 1. Если D = 0, то оно принимает вид Ах -f К + Cz = 0. Этому уравнению удовлетворяет точка 0. (0; 0; 0) Следовательно, в этом случае плоскость проходит через начало координат. . 2. Если С = 0, то имеем уравнение Ах -f- К + D = 0. Нормальный вектор п = <А; В; 0) перпендикулярен оси Оз Следовательно, плоскость параллельна оси Oz; если В = 0 — параллельна оси Оу , А = 0-параллельна ос Ох. 3. Если С = D = 0, то плоскость проходит через 0 (0; 0) 0 + Cz = 0. 4. Если А = В = 0, то уравнение (2) принимает вид Cz + D = 0>+ C (z-0) = 0.
т. е. 2 = — ^ 4. Плоскость параллельна плоскости Оху. уравнениям Ax + D = 0nBy + D = 0 взаимодействующих плоскостей, соответственно параллельных плоскостям Oyz и Ox yz 5. Если А = В = D = 0, то уравнению (2) примет вид Cz-О, т. Е. Z-0. Плоскости Oyz.
. Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость Найдем уравнение плоскости Q, проходящей через три данные точки Ми (XI; ил] Zi), М2 (х2; 2 / 25z2) и М3 (х3-, у3]. гз), не лежащие на одной прямой.
Уравнение плоскости, проходящей через три данные точки Людмила Фирмаль
Возьмем на плоскость спутника точку М (х; у; z) и составим предлагаемую MiM = (x-xi \ y-yi \ z-
zi), М \ М2y =) М \ М2y =) \ уг — 2/1; 2: 3
21) Эти векторы лежат на плоскости Q, следовательно, они компланарны Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем М \ М • М \ М2 • М \ М $ = 0, т. х-хх у-т / 1 z- Zi Xl -XI У2- У \ z2-Zi Хг -Xl 2/3-й Zt-Zi (4) = 0 Уравнение (4) есть уравнение плоскости, проходящее через три данные точки. 4. Уравнение плоскости в отрезках
Уравнение плоскости в отрезках Пусть плоскость пересекается на осях Ох, Оу и Оз соответственно соответственно отрезки, Ъ и с, т. П. Проходис Подставляя координаты этих точек в уравнение (4), получаем Раскрыв определитель, у нас hex-abc + abz -f асу = 0, т. Е. Ящик -I- асу 4- abz = abc или — +! + — =! • (5) азбука Уравнение (5) называется уравнением плоскости в отрезках на осях.
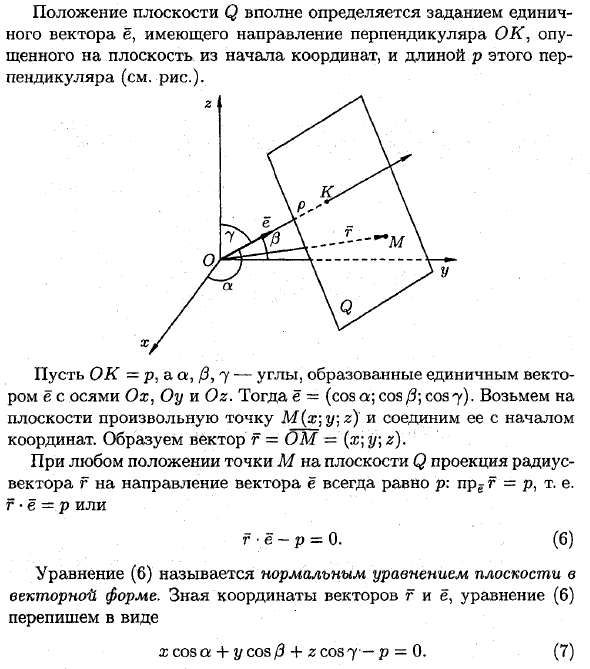
ПОЛОЖЕНИЕ В плоскости вполне определяется заданием единичного вектора ё, имеющего направление перпендикуляра ОК, опущенного на плоскость из начала координат, и длиной р этого перпендикуляра (см. Рис.). х
Пусть О К = р, а а, / 3,7 -. Углы, образованные единичный вектор с осями Ох, Оу и 02. Тогда ё = (потому что




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-vidy-uravnenija-ploskosti/
http://lfirmal.com/razlichnye-vidy-uravnenij-ploskosti-v-prostranstve/