Пояснить понятие функция заданная параметрическим уравнением

Параметрическое задание функции

Вы будете перенаправлены на Автор24

Параметрический способ задания функций

Пусть даны два уравнения

$x=\phi (t)$ и $y=\psi (t)$

В которых $t$ принимает значения с отрезка [n1; n2]. Каждому значению t соответствуют значения x и y — координаты точки на плоскости Оxy.

Когда $t$ изменяет свое значение на промежутке от $n1$ до $n2$, точка описывает некоторую кривую. Уравнения $x=\phi (t)$ и $y=\psi (t)$ получили название параметрических для кривой, а $t$ — параметра.

Предположим, что функция $x=\phi (t)$ имеет обратную функцию $t=\ (x)$. Тогда справедливо равенство:

Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны:

Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$.

Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$.

Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость:

А вертикальное перемещение:

Следовательно, расстояние от груза до земли в произвольный момент падения:

Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения.

Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории:

Готовые работы на аналогичную тему

Уравнения некоторых кривых в параметрической форме:

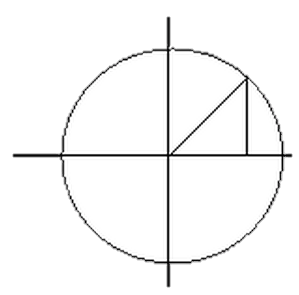
1. Окружность

Параметрические кривые окружности:

Рисунок 1. Окружность и ее параметрические кривые

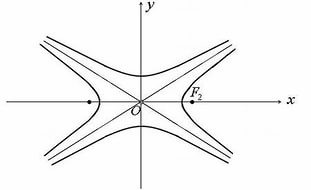
Уравнение гиперболы имеет вид:

Параметрические кривые гиперболы:

Рисунок 2. Гипербола и ее параметрические кривые

Записать уравнение окружности в параметрическом виде.

Представим уравнение окружности в виде: \[x^ <2>+y^ <2>=r^ <2>\] \[x^ <2>+y^ <2>=6^ <2>\]

Значит, радиус $r$ равен 6.

Записать уравнение гиперболы в параметрическом виде.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 11 12 2021

Параметрические уравнения прямой на плоскости: описание, примеры, решение задач

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Вывод параметрических уравнений прямой на плоскости

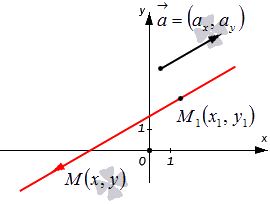
Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 ( x 1 , y 1 ) и направляющий вектор заданной прямой a → = ( a x , a y ) . Дадим описание заданной прямой a , используя уравнения.

Используем произвольную точку М ( x , y ) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = ( x — x 1 , y — y 1 ) . Опишем полученное: прямая задана множеством точек М ( x , y ) , проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) являются коллинеарными.

Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = ( x — x 1 , y — y 1 ) и a → = ( a x , a y ) возможно записать в виде уравнения:

M 1 M → = λ · a → , где λ – некоторое действительное число.

Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ

Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ

Составление параметрических уравнений прямой на плоскости

Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.

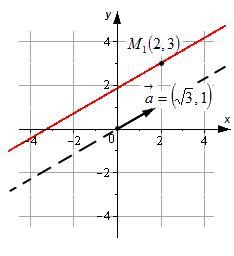
Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 ( 2 , 3 ) и ее направляющий вектор a → = ( 3 , 1 ) .

Решение

На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ

Ответ: x = 2 + 3 · λ y = 3 + λ

Необходимо отметить: если вектор a → = ( a x , a y ) служит направляющим вектором прямой а, а точки М 1 ( x 1 , y 1 ) и М 2 ( x 2 , y 2 ) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .

К примеру, нам заданы направляющий вектор прямой a → = ( 2 , — 1 ) , а также точки М 1 ( 1 , — 2 ) и М 2 ( 3 , — 3 ) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = — 2 — λ или x = 3 + 2 · λ y = — 3 — λ .

Следует обратить внимание и на такой факт: если a → = ( a x , a y ) — направляющий вектор прямой a , то ее направляющим вектором будет и любой из векторов μ · a → = ( μ · a x , μ · a y ) , где μ ϵ R , μ ≠ 0 .

Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.

Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = — 2 — 5 · λ . Тогда a → = ( 2 , — 5 ) — направляющий вектор этой прямой. А также любой из векторов μ · a → = ( μ · 2 , μ · — 5 ) = 2 μ , — 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор — 2 · a → = ( — 4 , 10 ) , ему соответствует значение μ = — 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 — 4 · λ y = — 2 + 10 · λ .

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x — x 1 a x = y — y 1 a y .

Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

При этом не должно смущать, если a x или a y будут равны нулю.

Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = — 2 — 4 · λ к каноническому уравнению.

Решение

Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = — 2 — 4 · λ

Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

x — 3 0 = y + 2 — 4

Ответ: x — 3 0 = y + 2 — 4

В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y ⇔ ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ A x + B y + C = 0

Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = — 1 + 2 · λ y = — 3 · λ

Решение

Для начала осуществим переход к каноническому уравнению:

x = — 1 + 2 · λ y = — 3 · λ ⇔ λ = x + 1 2 λ = y — 3 ⇔ x + 1 2 = y — 3

Полученная пропорция идентична равенству — 3 · ( x + 1 ) = 2 · y . Раскроем скобки и получим общее уравнение прямой: — 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .

Ответ: 3 x + 2 y + 3 = 0

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x — x 1 a x = y — y 1 a y . Каждое из отношений этого равенства примем равным параметру λ :

x — x 1 a x = y — y 1 a y = λ ⇔ λ = x — x 1 a x λ = y — y 1 a y

Разрешим полученные уравнения относительно переменных x и y :

x = x 1 + a x · λ y = y 1 + a y · λ

Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x — 2 5 = y — 2 2

Решение

Приравняем части известного уравнения к параметру λ : x — 2 5 = y — 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x — 2 5 = y — 2 2 = λ ⇔ λ = x — 2 5 λ = y — 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ

Ответ: x = 2 + 5 · λ y = 2 + 2 · λ

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x — 3 y — 3 = 0 .

Решение

Заданное общее уравнение преобразуем в уравнение канонического вида:

4 x — 3 y — 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4

Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:

x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = — 1 3 + 4 · λ

Ответ: x = 3 · λ y = — 1 3 + 4 · λ

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

1. В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.

Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.

Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 — 1 6 · λ y = — 1 + 2 · λ при λ = 3 .

Решение

Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 — 1 6 · 3 y = — 1 + 2 · 3 ⇔ x = 1 1 2 y = 5

Ответ: 1 1 2 , 5

Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .

Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.

Заданы точки М 0 ( 4 , — 2 ) и N 0 ( — 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = — 1 — 1 2 · λ .

Решение

Подставим координаты точки М 0 ( 4 , — 2 ) в заданные параметрические уравнения:

4 = 2 · λ — 2 = — 1 — 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2

Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .

Далее по аналогии проверим заданную точку N 0 ( — 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:

— 2 = 2 · λ 1 = — 1 — 1 2 · λ ⇔ λ = — 1 λ = — 4

Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( — 2 , 1 ) .

Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.

1. В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.

Пример 8

Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y — 3 — 1 .

Решение

По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y — 3 — 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y — 3 — 1 , который запишем в виде: a → = ( 2 , — 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( — 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 — λ

Ответ: x = 1 2 + x · λ y = 2 3 — λ .

Задана точка М 1 ( 0 , — 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .

Решение

В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , — 2 ) . Запишем требуемые параметрические уравнения прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = — 7 + ( — 2 ) · λ ⇔ x = 3 · λ y = — 7 — 2 · λ

Ответ: x = 3 · λ y = — 7 — 2 · λ

1. В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.

Пример 10

Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 — 3 4 · λ y = — 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

x = 1 — 3 4 · λ y = — 1 + λ ⇔ λ = x — 1 — 3 4 λ = y + 1 1 ⇔ x — 1 — 3 4 = y + 1 1 ⇔ ⇔ 1 · x — 1 = — 3 4 · y + 1 ⇔ x + 3 4 y — 1 4 = 0

Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 — 3 4 · λ y = — 1 + λ имеет координаты 1 , 3 4 .

Уравнения с параметрами.

Исследование и решение уравнений с параметрами считается не самым простым разделом школьной математики. Однако, параметр, как понятие, часто воспринимается школьниками гораздо более сложным, чем есть в действительности. Здесь в первом пункте представлены очень простые вводные примеры использования параметров в уравнениях. Те, для кого это понятие не составляет большой трудности, могут сразу перейти к решению задач, которые представлены ниже.

Что такое уравнение с параметром?

Допустим нам нужно решить уравнение 2х + 5 = 2 − x.
Решение: 2x + x = 2 − 5; 3x = −3; x = −3/3 = −1.

Теперь нужно решить уравнение 2x + 5 = 3 − x.
Решение: 2x + x = 3 − 5; 3x = −2; x = −2/3

Затем нужно решить уравнение 2x + 5 = 0,5 − x.
Решение: 2x + x = 0,5 − 5; 3x = −4,5; x = −4,5/3 = −1,5.

А потом может потребоваться решить уравнение 2x + 5 = 10,7 − x или уравнение 2x + 5 = −0,19 − x.
Понятно, что уравнения похожи, а потому их решение будет сопровождаться теми же действиями, что выше. Возникает естественный вопрос — сколько можно делать одно и то же?

Уменьшим себе трудозатраты. Заметим, что все эти уравнения отличаются только одним числом в правой части. Обозначим это число символом a .
Получим уравнение 2х + 5 = a − х,
где a — переменная величина, вместо которой можно подставить нужное числовое значение и получить нужное уравнение. Эта переменная и называется параметром.

Решим это уравнение так же, как и все предыдущие.
Решение: 2х + 5 = a − x; 2x + x = a − 5; 3x = a − 5; x = (a − 5)/3.

Теперь для того, чтобы найти ответы для двух последних примеров, мы можем не повторять полностью всё решение каждого уравнения, а просто подставить в полученную формулу для х числовое значение параметра а:
x = (10,7 − 5)/3 = 5,7/3 = 1,9;
x = (−0,19 − 5)/3 = −5,19/3 = −1,73.

Таким образом, под термином «уравнение с параметром», фактически, скрывается целое семейство «почти одинаковых уравнений» , которые отличаются друг от друга только одним числом (одним слагаемым или одним коэффициентом) и одинаково решаются. Параметр — это число, которое меняется от уравнения к уравнению.
Полученную формулу для корня уравнения мы можем запрограммировать на компьютере. Достаточно будет только ввести значение параметра a, чтобы получить решение любого такого уравнения.

Рассмотрим еще один пример.

Замечаем, что они похожи друг на друга и отличаются только первым коэффициентом. Обозначим его, например, символом k.
Решим уравнение kх + 5 = 2 − x с параметром k.

С помощью этой формулы вычислим все ответы для приведенных уравнений.
x = −3/(2 + 1) = −1
x = −3/(3 + 1) = −0,75
x = −3/(−4 + 1) = 1
x = −3/(17 + 1) = −1/6

Можем ли мы теперь запрограммировать эту формулу и сказать, что с её помощью можно решить любое аналогичное уравнение?
Запрограммировать можем. Компьютер справится как с очень большими значениями коэффициента, так и с очень маленькими.
Например, если введём k = 945739721, то для уравнения заданного вида будет получен корень примерно равный −0,0000000031721201195353831188, если k = 0,0000004, то получим корень ≈ −2,9999988000004799998080000768.
Но, если мы введем в программу, казалось бы, более простое значение k = −1, то компьютер зависнет.
Почему?

Посмотрим внимательнее на формулу x = −3/(−1 + 1) = −3/0. Деление на ноль.
Посмотрим на соответствующее уравнение −1·х + 5 = 2 − x.
Преобразуем его −х + x = 2 − 5.
Оказывается, оно равносильно уравнению 0 = −3 (. ) и не может иметь корней.
Таким образом, из общего подхода к решению «почти одинаковых уравнений» могут существовать исключения, о которых нужно позаботиться отдельно. Т.е. провести предварительное исследование всего семейства уравнений. Именно этому и учатся на уроках математики с помощью так называемых задач с параметрами.

Графические способы решения уравнений

Сначала вспомним, что представляет собой графический способ решения обычного уравнения (без параметра).
Пусть дано уравнение вида f(x) = g(x) . Построим графики функций y = f(x) и y = g(x) и найдём точки пересечения этих графиков. Абсциссы точек пересечения и есть корни уравнения.

Для быстрого построения эскизов графиков повторите еще раз графики элементарных функций, которые изучаются в школьном курсе математики, и правила преобразования графиков функций.

Рассмотрим примеры.

1. Решить уравнение
2х + 5 = 2 − x

Ответ: x = −1.

2. Решить уравнение
2х 2 + 4х − 1 = 2х + 3

3. Решить уравнение
log₂х = −0,5х + 4

Ответ: x = 2.

Первые два из приведенных уравнений вы можете решить и аналитически, так как это обычные линейное и квадратное уравнения. Второе уравнение содержит функции разных классов — степенную (здесь линейную) и трансцендентную (здесь логарифмическую). Для таких случаев выбор способов решения у школьников очень ограничен. Фактически, единственным доступным способом является именно графическое решение.

Внимание: Для корней, найденных графическим способом, обязательна проверка! Вы уверены, что на третьем рисунке пересечение именно в точке х = 4 , а не в точке 3,9 или 4,1? А если на реальном экзамене у вас нет возможности построить график достаточно точно? На чертеже «от руки» разброс может быть еще больше. Поэтому алгоритм действий должен быть следующим:

1. Предварительный вывод: х ≈ 4.
2. Проверка: log₂4 = −0,5·4 + 4; 2 = −2 + 4; 2 ≡ 2.
3. Окончательный вывод х = 4.

Чтобы графически решать уравнения с параметрами надо строить не отдельные графики, а их семейства.

Решение уравнений с параметрами с помощью графиков.

Задача 1.

Найти все значения параметра q при которых уравнение |x + 1| − |x − 3| − x = q 2 − 8q + 13 имеет ровно 2 корня.

При каждом значении параметра q можно вычислить значение выражения q 2 − 8q + 13 . Результат обозначим переменной а.
Т.е. примем q 2 − 8q + 13 = a и решим уравнение с параметром |x + 1| − |x − 3| − x = a

Строим график функции y = |x + 1| − |x − 3| − x , расположенной в левой части уравнения.
Для этого разобьём числовую ось на отрезки точками, в которых каждый из встречающихся модулей принимает нулевое значение.

Для каждого из этих участков раскроем модули с учётом знаков.
Вспомним: по определению |x| = x, если х ≥ 0, и |x| = −x, если х Чтобы проверить знаки модулей на участке достаточно подставить любое промежуточное значение x из этого отрезка, например, −2, 0 и 4.

Таким образом на участке I, где −∞ имеем −(x + 1) + (x − 3) − x = − x − 4.
Следовательно, должны построить график функции y = − x − 4 .
Это линейная функция. Её график прямая линия, которую можно построить по двум точкам, например, x = 0, y = −4 и у = 0, x = −4. Cтроим всю прямую бледной линией, а затем выделяем часть графика, относящуюся только к рассматриваемому участку.

Аналогично, разбираемся с оставшимися двумя участками.

На участке II, где −1 имеем (x + 1) + (x − 3) − x = x − 2
и должны построить соответствующую часть графика функции y = x − 2 .

На участке III, где 3 , имеем (x + 1) − (x − 3) − x = − x + 4
и должны построить соответствующую часть графика функции y = − x + 4 .

Последовательное построение итогового графика показано ниже. (Чтобы увеличить рисунок, нужно щелкнуть по нему левой кнопкой мыши.)

Замечание: если вы освоили тему Преобразование графиков функций, то с этой частью задачи сможете справиться быстрее, чем показано в примере.

Итак, построение графика функции, расположенной в левой части уравнения, мы завершили. Посмотрим, что находится в правой части.

График функции y = a представляет собой прямую линию, параллельную оси абсцисс (Ox), и пересекающую ось ординат (Oy) в точке а. Так как а — параметр, который может принимать разные значения, то нужно построить целое семейство таких параллельных линий, пересекающих ось ординат на разной высоте. Очевидно, что все графики семейства построить мы не сможем, поскольку их бесконечное множество. Изобразим для примера несколько штук в районе уже построенного графика функции. Ниже прямые семейства y = a показаны красным цветом.

Из рисунка видно, что количество точек пересечения каждой из красных прямых с ранее построенным (зелёным) графиком зависит от высоты, на которой расположена эта прямая, т.е. от параметра а. Прямые, расположенные ниже y = −3 , пересекают график в одной точке, а значит эти уравнения имеют только одно решение. Прямые, проходящие на уровне −3 имеют по три точки пересечения, значит соответствующие уравнения будут иметь по три решения. Прямые, расположенные выше точки y = 1 , снова имеют только по одной точке пересечения.
Ровно две точки пересечения с зелёным графиком будут иметь только прямые y = 1 и y = −3 . Соответствующие уравнения будут иметь ровно два корня, что и требовалось определить в задании.

Однако мы нашли значения введённого нами параметра а, при котором заданное уравнение имеет 2 корня, а вопрос задачи состоял в том, чтобы найти все значения параметра q. Для этого придётся решить следующую совокупность уравнений:

Это обычные квадратные уравнения, которые решаются через дискриминант или по теореме Виета.

Таким образом, окончательный ответ: <2;4;6>.

Задача 2.

Найти все значения параметра a, при которых уравнение (2 − x)x(x − 4) = a имеет ровно 3 корня.

Рассмотрим функцию y = (2 − x)x(x − 4) . Видно, что если раскрыть скобки, то старший член будет −х 3 . Т.е. графиком функции должна быть кубическая парабола, причем на при x, стремящемcя к +∞, y → −∞, а при x, стремящемся к −∞, y → +∞.
Поскольку уравнение (2 − x)x(x − 4) = 0 имеет три корня 2, 0 и 4, то график функции будет пересекать ось абсцисс трижды.
Понятно, что при упомянутых условиях график непрерывной функции должен иметь участок с «волной». Строим от руки эскиз графика.

Правая часть уравнения y = a такая же, как в предыдущей задаче. Поэтому дальнейшие построения не требуют комментариев. Смотрите рисунки. Чтобы увеличить, используйте щелчок мышью.

Из рисунков видно, что прямые, отделяющие линии с тремя точками пересечения от других случаев, проходят через экстремумы кубической функции. Поэтому определяем значения y_max и y_min через производную. (Исследовать функцию полностью не нужно, так как примерное положение точек экстремума мы видим на эскизе графика.) Обратите внимание на то, что при вычислении значений функции используются точные значения x и формулы сокращенного умножения. Приближенные значения в промежуточных вычислениях не используют.

Ответ:

Задача для самостоятельного решения

Задача 3.

При каком наибольшем отрицательном значении параметра а уравнение имеет один корень?

Ответ: -1,625

Задача реального экзамена ЗНО-2013 (http://www.osvita.ua/).

Переход на главную страницу сайта «Математичка».

Есть вопросы? пожелания? замечания?
Обращайтесь — mathematichka@yandex.ru

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.