Практическая работа по теме: «Решение показательных уравнений и неравенств»
Просмотр содержимого документа
«Практическая работа по теме: «Решение показательных уравнений и неравенств»»
Практическая работа №3
Тема: «Решение показательных уравнений и неравенств»
Цель: научиться применять свойства показательной функции для решения показательных уравнений и неравенств, закрепить знания и умения по применению методов решения показательных уравнений и неравенств для решения практических задач.
Основные теоретические положения
Определение. Уравнение вида 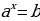
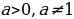
Если
Способы решения показательных уравнений.
1. Уединить слагаемое, содержащее переменную;
2. Привести степени к одному основанию;
3. Приравнять показатели;
4. Решить полученное уравнение;
5. Записать ответ.
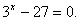
Вынесение общего множителя за скобки.
Примечание: выносим за скобки множитель с меньшим показателем.
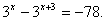
Введение новой переменной
Как правило, уравнения, решаемые этим способом, сводятся к квадратным.
Пример:
Пусть 4 x = а тогда уравнение можно записать в виде:
Сделаем обратную замену:
4 x = 4 или 4 x = 1;
х = 1 или х = 0
Ответ: х = 1 или х = 0
Определение Показательные уравнения вида 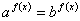
Суть метода: Так как показательная функция не может принимать значение, равное нулю, и обе части уравнения можно делить на одно и то же не равное нулю число, разделим обе части уравнения, например, на 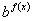
Разделим обе части уравнения на
Определение. Показательным неравенством называется неравенство, в котором переменная содержится в показателе степени.
Решение простейших показательных неравенств.
Простейшими считаются показательные неравенства вида: a x y , a x a y . (a x ≤a y , a x ≥a y ).
Так же, как и при решении простейших показательных уравнений, одинаковые основания степеней опускают, но знак нового неравенства сохраняют, если функция у=а х является возрастающей (а1); eсли же показательная функция у=а х убывает (0), то знак нового неравенства меняют на противоположный:
a x a y → x y, если a1; знак сохранен, так как функция возрастает;
a x a y → x y, если 0; функция убывает – знак поменялся;
a x a y → x y, если a1; знак сохранен, так как функция возрастает
a x a y → x y, если 0; функция убывает – знак поменялся.
Представим правую часть в виде: 0,25=( 25 /100)=( 1 /4)=4 -1 ;
4 5-2x -1 ; функция у=4 х с основанием 41 возрастает на R, поэтому, опуская основания степеней, знак неравенства сохраним:
Представим число 0,16 в виде степени числа 0,4. Получаем:
0,4 2х+1 ≥0,4 2 ; основание степеней – число 0,4 — удовлетворяет условию: 0; поэтому, опускаем основания степеней, а знак неравенства меняем на противоположный:
2 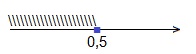
1)
2)
6)
3)
4)
7)
Решите систему уравнений
5)
8)
9)
1)
2)
6)
3)
4)
7)
Решите систему уравнений
5)
8)
9)
1)
2)
6)
3)
4)
7)
Решите систему уравнений
5)
8)
9)
1)
2)
6)
3)
4)
7) 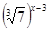
Решите систему уравнений
5)
8)
9)
Сделайте вывод по проделанной работе
От чего зависит возрастание или убывание показательной функции?
Дайте определение показательного неравенства.
Какие условия должны выполняться при решении показательных неравенств?
Практическая работа «Показательные неравенства».
Практическое занятие: Показательные неравенства.
Цель: освоить решение показательных неравенств .
1. Для того, чтобы освоить решение показательных неравенств необходимо:
1) знать и уметь решать показательные уравнения;
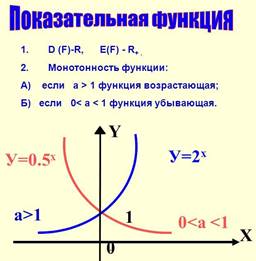
2) знать и уметь применять признак монотонности (возрастания и убывания) показательной функции;
3) уметь решать простейшие неравенства (линейные, квадратные)
— По первому пункту вы сдали зачёт – решение показательных уравнений освоили.
— По второму пункту мы проводили исследовательскую работу: строили графики показательных функций и обобщили признаки возрастания и убывания функций по их формулам.
— Повторением способов решения простейших линейных и квадратных неравенств,; правил, связанных с решением неравенств, мы будем заниматься сегодня.
2. Познакомьтесь с материалом, вспомните или изучите решение простейших линейных неравенств, сделайте конспект и выполните самостоятельную работу,
Материал для повторения:
1) Изображение, обозначение числовых промежутков.
2) Правила преобразования неравенств, приводящие к равносильным неравенствам.
3). Запишите примеры решения линейных неравенств.
4). Решите самостоятельно неравенства:
3. Познакомьтесь с материалом, вспомните или изучите решение простейших квадратных неравенств, сделайте конспект и выполните самостоятельную работу.
Материал для повторения:
Решите самостоятельно неравенства:
4.Повторите свойство показательных функций на возрастание и убывание (монотонность).
Укажите из перечисленных показательных функций возрастающие и убывающие:
y =( 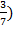
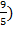
5.Решение показательных неравенств.
Метод приведения к одному основанию.
Пример 1 . Решить неравенство:
Перепишем неравенство: 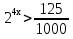
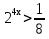
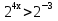
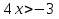
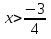
Ответ: х € 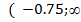
Метод вынесения общего множителя за скобки.
Пример 2. Решить неравенство: 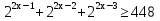
Потому что за скобки выносится наименьшая степень.
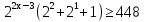
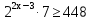
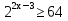
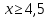
Ответ: 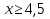
Метод введения новой переменной.
Пример 3. Решить неравенство: 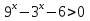
Здесь, как вы видите, лучше использовать Пусть 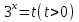
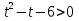
У нас получилось квадратное неравенство.
Для начала найдём корни, т.е. от неравенства перейдём к уравнению: 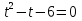
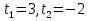
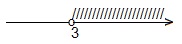
Отмечаем их на числовой прямой, у нас получилось 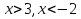
1) Неравенство 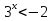
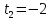
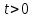
2) 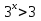
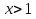
Ответ:
Решите самостоятельно неравенства:
Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://znanio.ru/media/prakticheskaya-rabota-pokazatelnye-neravenstva-2666846
http://www.evkova.org/pokazatelnyie-uravneniya-i-neravenstva

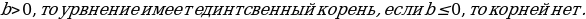
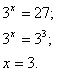

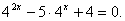
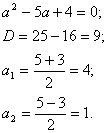
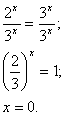
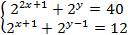
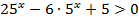
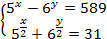


















































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);










