Практическая работа приближенное решение уравнений

Практическая работа Приближенное решение уравнений

Практическая работа

Приближенное решение уравнений

Просмотр содержимого документа
«Практическая работа Приближенное решение уравнений»

Приближенное решение уравнений

Создать компьютерную модель «Приближенное решение уравнений» с использованием электронных таблиц Microsoft Excel, которая позволяет найти корень уравнения x 3 = sin x приближенными методами (графическим и с помощью метода Подбор параметра).

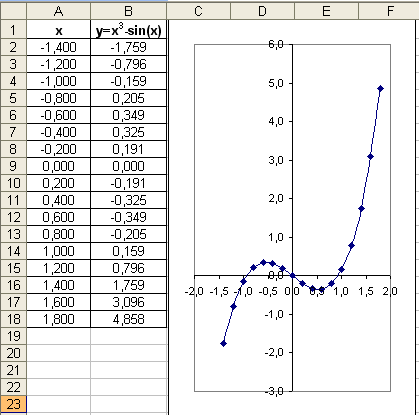
Представить функцию в табличной форме, построить ее график, который позволит определить корни уравнения грубо приблизительно.

Представить заданное уравнение в табличной форме.

Для грубо приближенного определения корня построить диаграмму типа график. По графику грубо приближенно можно определить, что х=0,8.

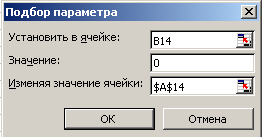
Для поиска решения с заданной точностью используем метод Подбор параметра. Точность подбора зависит от заданной точности представления чисел в ячейках таблицы (например, до трех знаков после запятой). Методом подбора параметра необходимо определить значение аргумента х (ячейка В14) равно нулю.

Выделить ячейку со значением функции В14 и ввести команду [Сервис-Подбор параметра…].

На панели Подбор параметра в поле Значение ввести требуемое значение функции (в данном случае 0).

В поле Изменяя значение ячейки ввести адрес ячейки $А$14, в которой будет производиться подбор значения аргумента, и щелкнуть по кнопке ОК.

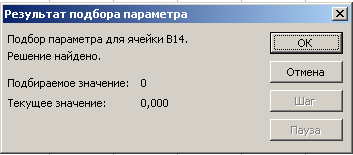
На панели Результат подбора параметра будет выведена информация а величине подбираемого и подобранного значений.

В ячейке аргумента А14 появится подобранное значение 0,929. Таким образом, корень уравнения х=0,929 найден с заданной точностью.

Аналогично определите второй корень уравнения.

Задание для самостоятельной работы. Создать компьютерную модель «Приближенное решение уравнений» с использованием электронных таблиц Microsoft Excel, которая позволяет найти корень уравнения х 3 = sin х графическим способом.

Лабораторная работа по теме «Приближенное решение уравнений»

Цели:

• образовательные – познакомить учащихся с историческими сведениями по теме «Решение уравнений высших степеней», практическим применением математических моделей к решению уравнений, различными способами решения уравнений, в том числе и приближенными; формировать представление о применении ЭВМ для автоматизации решений, продолжить знакомство с программой Microsoft Excel, языком программирования Паскаль, познакомить учащихся с пакетом САПР MathCAD;
• развивающие – развивать логическое мышление, память, внимание, критическое мышление, умение сравнивать и анализировать;
• воспитательные – воспитывать трудолюбие, умение работать в группе, культуру речи и общения, самостоятельность.

Тип урока: лабораторная работа с применением мультимедиа-презентации

План урока:

• 1. Организационный момент.(1 мин)
• 1.1. Приветствие учителя и учеников.
• 1.2. Проверка присутствующих.
• 2. Объявление темы и целей урока — (1 мин)
• 3. Историческая справка. мультимедиа-презентация Слайд № 1-15 — (8 мин)
• 3.1. Практическое значение решения уравнений. Слайд № 1-2.
• 3.2. Что такое уравнение? Слайд № 3-4
• 3.3. Исторические сведения об открытии способов решения уравнений. Слайд № 5-15
• 4. Изучение нового материала слайд 16 -21. (8 мин)
• 4.1. Графический метод — Слайд 16-17.
• 4.2. Подбор параметров в Excel. Слайд 18.
• 4.3. С помощью пакета САПР MathCAD — Слайд 19.
• 4.4. Метод простой итерации – Слайд 20.
• 4.5 Метод половинного деления Слайд 21.
• 5. Закрепление материала. Лабораторная работа. (22 мин).
• 5.1. Выдача заданий и форм отчета группам. (2 мин).
• 5.2 Работа над лабораторной работой, заполнение отчетов. (17 мин).
• 5.3. Доклад группы по отчету. Вывод по лабораторной работе. (5 мин)
• 6. Итоги занятия. (3 мин)
• 6.1. Выставление оценок
• 7. Домашнее задание.(2 мин)
• 8. Завершение урока.

ХОД УРОКА

1. Организационный момент.

Приветствие учителя и учеников. Проверка присутствующих.

2. Объявление темы и целей урока.

Слайд 1. Мультимедиа-презентация.

2.1. Учитель. Продолжаем изучать одну из самых интересных, научно-обоснованных тем курса информатики: Моделирование. Тема урока – “Лабораторная работа. Приближенное решение уравнений”. Мы проследим путь ученых от древности до наших дней. Рассмотрим различные способы решения уравнений. И сами решим некоторые сложные уравнения в группах самостоятельно. Причем каждая группа получит своё задание, а в конце урока мы сравним полученные результаты и оценим работу групп. Поздравляю Вас! Сегодня у нас настоящий научный эксперимент! В завершении урока запишем д/з.

2.2. Цель урока – познакомиться с ещё одним применением математических моделей: решением уравнений приближенными методами.

3. Историческая справка. мультимедиа-презентация

3.1. Практическое значение решения уравнений. Слайд № 1-2.

Учитель. Математика одна из самых практичных наук. Она родилась из задач, которые перед людьми ставила жизнь: как поделить наследство, как лучше распахать землю, как рассчитать налог и т.д. Оказывается, многие практические задачи приводят к решению уравнений. Слайд № 2. Задачи земледельцев: нахождение площадей геометрических фигур приводит к решению квадратного уравнения. Нахождения объема — приводит к решению уравнений третьей степени. Другая задача о точности стрельбы пушки — это классическое решение используется до сих пор в баллистике и приводит к решению уравнений третьей степени . Проблемы выращивания искусственных кристаллов – уравнения четвертой и пятой степени. Расчет длины и угла наклона крыльев самолёта и других летательных аппаратов – квадратные и кубические уравнения и т.д.

3.2. Что такое уравнение? Слайд № 3-4

Учитель. Вы, конечно, знакомы с понятием «уравнение». Одно из определений уравнения Вы видите на слайде. Также Вы знакомы с разнообразными видами уравнений. Первое и второе, а может быть и третье уравнение, Вы сможете решить обычными методами. Какими? (Перенести неизвестные в одну сторону, известные в другую для первого уравнения, для второго теорема Виета или через дискриминант). Верно. А как Вы думаете: в древности люди пользовались такими же методами? (….) А кто придумал современные методы решения и всегда ли они применимы? Например, для такого примера (Слайд 4), да если учесть, что n – любое натуральное число? (Наверное, нет). Вот решение таких уравнений интересовали ученых с давних времен.

3.3. Исторические сведения об открытии способов решения уравнений. Слайд № 5-14

Учитель. Слайд 5. «В Древнем Вавилоне грамотные люди (ими чаще всего были жрецы и чиновники) умели решать довольно сложные уравнения, в том числе и уравнения второй степени.» [17] Всё решение записывалось словами, не было никакой математической символики: ни переменных, ни знаков действий, ни знака равенства. Задачи, сводящиеся к решению квадратного уравнения «…вавилоняне часто рассматривали как задачи на определение длины и ширины прямоугольника по известной его площади и либо сумме длины и ширины (…), либо «избытку длины над шириной» (мы бы просто сказали – разности). Иначе говоря, х₁ – длина, х₂ – ширина, р – площадь, р – сумма длины и ширины». [17] Не правда ли, почти теорема Виета? «Евклид (III в. до н.э.) решал квадратные уравнения, применяя геометрический способ.» [17]

Слайд 6. Знаменитый Аль Хорезми упростил решение уравнений: он предлагает решение нескольких типов квадратных уравнений.

Слайд 7. Кроме того, он мог решать простейшие уравнения третьей степени: х 3 = 27.

Слайд 8. «Замечательный таджикский поэт и ученый Омар Хойям (ок. 1048- ок. 1123), «конечно, без буквенной символики и отрицательных чисел – описал все возможные виды уравнений третьей степени и рассмотрел способ их решения… Первое слагаемое можно понимать как куб с ребром х. Произведение рх 2 – это прямоугольный параллелепипед с высотой р и квадратным основание, причем сторона основания х. Слагаемое qx = . Это … ещё один прямоугольный параллелепипед с основанием х 2 и высотой q/x.» [17]. Уже в то время ученые задумывались об общих способах решения задач. Ведь очень трудно придумывать каждый раз новое решение. «В школьных учебниках по математике, как и в других книгах, большинство способов решений рассматриваются в общем виде, а не на конкретных примерах. Но сами математические открытия делаются не в общем виде. Очень часто – почти всегда – математик ищет частные примеры, подтверждающие или опровергающие его мысль. Если пример приведет к опровержению мысли – поиск ведётся в новом направлении. Если пример подтвердит её – ищут общее доказательство.» [17]. К сожалению, придумать геометрическое решение для задач четвертой, а тем более пятой степени уже сложно, а в те времена было невозможно.

Слайд 9. «Со времён Омара Хайяма ученые искали формулу решения уравнений третьей степени почти четыреста лет… Были периоды, когда начинало казаться, что сил человеческого ума для решения этой задачи недостаточно. .. Томас Торквемада (1420 – 1498) — … считал, что решение таких уравнений волей бога изъято из возможностей человеческого разума. И когда один из его друзей, математик по имени Паоло Вальмес, неосторожно сказал …, что он умеет решать уравнения даже четвертой степени, Торквемада бросил его в тюрьму, а затем отправил на костер за «Борьбу с божественной волей». [17].

Слайд 10. Времена были суровые, но даже тогда тот, кто владел информацией, тот владел миром! И человек, который единственный в своей стране или в целом мире умел быстро и правильно решать кубические уравнения, был очень влиятельной особой приближенной к властителям мира. Первым таким ученым был итальянский математик Сципион Даль Ферро (1465 – 15260. Даль «Ферро не опубликовал своё открытие, но некоторые ученики знали об этом, и вскоре один из них, Антонио Фиор, решил этим воспользоваться. В те годы были распространены публичные диспуты по разного рода научным или считавшимися научными вопросам. Победители таких диспутов получали неплохое вознаграждение, их часто приглашали на высокие должности, от исхода научного поединка нередко зависела судьба ученого… » [17]

Слайд 11. Честь же ученого, уже в преклонных летах, решился защитить обыкновенный школьный учитель математики, который даже не был учеником Сципиона Ферро , а всего лишь поклонником таланта ученого. Этот Никколо (1499-1557), «прозванный Тарталья, т.е. заика, был очень талантливым человеком и сумел заново открыть прием Сципиона… По условию соперники обменялись тридцатью задачами, на решение которых отводилось 50 дней. Но так как Фиор знал по существу лишь одну задачу и был уверен, что какой-то учитель решить её не сможет, то все тридцать его задач оказались однотипными.» [17]. Тарталья решил эти задачи за два часа. «Фиор не смог решить ни одной из задач… Победа прославила Н. Тарталья на всю Италию…

Ещё один ученый, Д. Кардано, был выдающимся врачом, философом, математиком и механиком (все, кто имеет отношение к автомашинам, знают о так называемой карданной передаче)…» [17] В его книге об алгебре он предложил алгебраическую формулу для решения кубического уравнения, которая теперь называется формулой Кардано, ею пользуются до сих пор.

Слайд 12. Франсуа Виет (1540-1603) – французский математик мечтал вывести подобную формулу (пусть и достаточно громоздкую) для уравнений пятой степени. Кстати, а почему мы пропускаем уравнения четвертой степени? (Они сводятся к биквадратным уравнениям). Верно, также как уравнения шестой степени к уравнениям третьей степени, а уравнения восьмой степени – к уравнениям четвертой степени и т.д. Франсуа Виет, решая уравнения пятой степени, придумал нечто другое: «Виет первым догадался обозначать буквами не только неизвестные, но и коэффициенты при них. Подумайте, сами, какой огромный шаг вперёд означало это, казалось бы, очень скромное новшество… Недаром Виета часто называют «отцом алгебры». [17] Именно он открыл теорему Виета и способ подбора корней как делителей свободного члена.

Слайд 13. Поиски общей формулы для решения уравнений четвертой, пятой степени продолжались достаточно долго. Пока задача не приняла вид вопроса: существует ли вообще решения уравнений произвольных степеней в радикалах? «Требование «найти формулу» вполне понятно. А требование доказать, что такой формулу не существует звучит менее привлекательно, и оказалось, что получение отрицательного ответа требует создания совершенно нового направления в алгебре». [17]. Занимались таким доказательством несколько ученых: Паоло Руффини (1765 – 1822) – итальянский ученый (доказательство неполное), Жозеф Луи Лагранж (1736-1813) – французский математик и механик (был близок к решению).

Слайд 14. Нильс Хенрик Абель (1802 – 1829) – норвежский математик и Эварист Галуа (1811 – 1832) – французский математик. Несмотря на молодость, они смогли найти безупречное доказательство неразрешимости в радикалах уравнений пятой степени.

Слайд 15. Таким образом, не существует формул, приводящих к точному нахождению корней уравнений высших степеней (четвертой, пятой и т.д.). На слайде представлены некоторые методы решения уравнений. Вы, наверное, удивитесь, что те уравнения, которые встречаются в учебнике и могут быть решены простыми методами: разложение на множители или введение нового неизвестного (в случае биквадратных уравнений) – это лишь одна десятитысячная всех уравнений, которые приходится решать человечеству. Остальные решения находятся методами приближенного вычисления. Эти методы удобны для применения ЭВМ.

4. Изучение нового материала.

4.1. Графический метод — Слайд 16-17.

Учитель. Для удобства вычислений уравнению присваивают имя функции: уравнение х 4 +5х-3=0 это функция у(х)= х 4 +5х-3. Если значение функции равно нулю при некотором значении х, то х – искомый корень уравнения.Естественно, что приближенные методы используются в трудных случаях, когда сложно найти корень, поэтому у(х)=0,0001 – некоторая величина, близкая к нулю. Это значение – точность вычислений.Этот метод очень прост. По известному уравнению вычисляются несколько значений функции (значение переменной х изменяется с определенным шагом: на рисунке это 0,1) и строиться примерный график функции. Естественно, чем меньше шаг, тем точнее график. Самое доступное средство – электронная таблица Excel. По графику можно найти корень уравнения – это точка пересечения графика функции с осью абсцисс. Это корень, найденный с точностью не более 0,1. Слайд 17. Часто этой точности не достаточно. Тогда этот метод лишь указывает нам промежуток, на котором можно найти корень, используя другие приближенные методы.

4.2. Подбор параметров в Excel. Слайд 18.

Учитель. Первый метод автоматического нахождения корней: метод подбора параметров в электронной таблице Excel. Можно воспользоваться уже введенной формулой для построения графика, а затем выбрать в меню Сервис – Подбор параметра. В появившемся диалоговом окне в поле Установить в ячейке ввести адрес В4; в поле Значение 0; в поле Изменяя значение ячейки ввести адрес А4, в которой будет производиться подбор значения аргумента. Нажать ОК. На панели Результат подбора параметра будет выведена информация о величине значения функции 0,000554912, а в ячейки аргумента А4 появится подобранное значение 0,999. [2, 3].

4.3. С помощью пакета САПР MathCAD — Слайд 19.

Учитель. Второй метод – использование специального пакета САПР MathCAD. Эта специализированная программа, включающая более 20 тысяч автоматических функций, таких как вычисление производной, разложение на множители многочлена, вычисление неопределенных интегралов (символьные вычисления), определенных интегралов, построение графиков функций и т.д. Этой программой пользуются не только профессиональные математики, но и инженеры. Программа позволяет полностью подготовить пакет проектных документов: графики, схемы, расчеты (в том числе с помощью встроенного средства программирования), и даже пояснительную записку в удобном текстовом редакторе. Все элементы проекта готовятся в одном документе, все формулу и графики связаны между собой и при смене входных данных происходит автоматический пересчет параметров и графиков, схем. 12

4.4. Метод простой итерации – Слайд 20.

Учитель. Третий метод – метод простой итерации. Суть метода похожа на графический метод: выбирается отрезок, содержащий корень уравнения. Для этого достаточно наугад взять два значения аргумента, например, 5 и -5, и вычислить значения функции. Если значения функции имеют разные знаки, то на данном промежутке существует искомый корень. Если нет, подбирают другие значения. Затем выбирают шаг вычислений (также как при построении графика функции). Последовательно вычисляя значения функции, сравниваем модуль значения с точностью вычисления. Процесс останавливается, если точность вычисления достигнута. Но этот метод не всегда приводит к нужному ответу. Как Вы думаете почему? (Можно пропустить корень).

4.5 Метод половинного деления Слайд 21.

Учитель. Последний, изучаемый нами метод – метод половинного деления. Выбирается отрезок, содержащий корень уравнения. И делится пополам (отсюда и название метода). Вычисляем значение функции в середине отрезка и сравниваем с заданной точностью, если точность не достигнута, выбираем из двух отрезков тот, который содержит корень. Напомните, как это сделать? (На концах отрезка, содержащих корень, значения функции разных знаков). После выбора отрезка, другой отрезок больше не рассматриваем. Выбранный отрезок делим пополам, вычисляем значение функции в середине, сравниваем с точностью, если нужно, снова выбираем новый отрезок и т.д. В этом случае можно достигнуть любой точности вычислений. Но поиск решения может и затянуться.

5. Закрепление материала. Лабораторная работа.

5.1. Выдача заданий и форм отчета группам.

Учитель Задача нашего урока: самим попробовать вычислить корни трех уравнений различными методами. Для этого воспользуемся электронной таблицей Excel. Но, поскольку, мы ограничены рамками урока, будет удобнее разделиться на две группы и сравнить результаты экспериментов по окончанию работы.

Учащиеся делятся на две группы, получают по три экземпляра бумажных заданий с инструкциями по выполнению , файл электронного отчета храниться на рабочем столе каждого компьютера под названием «Отчет по лабораторной работе Приближенные вычисления для первой группы», «Отчет по лабораторной работе «Приближенные вычисления « для второй группы». .

Учитель Каждая группа получает инструкцию, в которой указан порядок выполнения работы и порядок заполнения электронного отчета по результатам эксперимента. В конце урока результаты эксперимента должен презентовать ответственный представитель группы.

5.2. Работа над лабораторной работой, заполнение электронных отчетов.

Во время лабораторной работы можно включить тихую музыку. Группа обсуждает план действий. Выбирает ответственного за представление результатов эксперимента ученика, наиболее компетентного члена группы. Если группы большие, по 10 человек, то можно подсказать, чтобы учащиеся распределили задания: первый компьютер – первое уравнение, второй компьютер – второе уравнение и т.д. За один компьютер садятся два-три человека, один ученик набирает выражение, второй — диктует и контролирует, третий — фиксирует время работы. Функция учителя сводится к контролю времени и участия всех членов группы в работе. Все вопросы по выполнению задания, должны быть адресованы к ответственному представителю группы. После окончания работы в мини-группах ответственные проверяют результаты, готовятся к выступлению.

5.3. Доклад группы по отчету. Вывод по лабораторной работе.

(Музыка сменяется звуковым сигналом СТОП, можно использовать звук фанфар).

Учитель. Прошу ответственных представителей переслать электронные отчеты на главную машину. (Учитель открывает сразу два отчета на странице: слева отчет первой группы, справа – второй группы). Презентация результатов начинается с первой группы.

Представитель первой группы. (Пример решения ). Решая первое уравнение всеми тремя методами мы нашли корень х=1. Но решая последним методом затратили наименьшее количество времени. Все методы привели к нужному результату, точность тоже была одинакова. В этой задаче можно было обойтись и без этих методов.

Представитель второй группы. Мы решали методом половинного деления, но у нас те же результаты. И задача решается устно.

Учитель. Хорошо, тогда вторая группа презентуйте решение второй задачи.

Представитель второй группы. Эту задачу, наверное, в ручную сложно решить. Ответы во всех методах разные. Самый быстрый и точный – подбор параметров, самый не результативный – графический. Но метод половинного деления самый длинный и сложный. Хотя у нас было всего четыре шага. (Пример решения второго уравнения первой и второй группой ).

Учитель. Вывод первой группы.

Представитель первой группы. По графическому и методу подбора параметра результаты те же. Метод простой итерации занял меньше времени, чем у второй группы, но у нас 22 вычисления, но ответ у них значительно точнее.

Аналогично, обсуждаются третья задача. Основной контролируемый учителем критерий ответа: соответствие выводов полученным результатам и оценки эффективности всех трех методов.

Обобщающий вывод: эффективность применения трех методов по трём задачам.

Учитель. Выяснилось, что в зависимости от задачи, эффективным может оказаться любой из приближенных методов. Но метод простой итерации может не дать ответа (пропустить его). Обратите внимание, что метод половинного деления и простой итерации – основа встроенных функций Подбор параметра и функции root пакета САПР MathCad. Поэтому, неудивительно, что Вы решали медленнее, чем компьютер. Но эти задачи хорошо программируются.

6. Итоги занятия. (3 мин)

6.1. Выставление оценок. Учитель выставляет оценку представителю группы за выступление, за умение обобщить выводы, сравнить результаты своей группы с результатами другой группы, участникам группы за правильность выполнения заданий (верное применение метода, оформление отчета, соответствие результатов сделанным выводам, степень участия в работе группы).

7. Домашнее задание. (2 мин)

Составить блок-схему для решения уравнений методом простой итерации (для 2 группы), методом половинного деления (для 1 группы).

Практическая работа «Графическое решение уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Приближенное решение уравнений графическим методом и с помощью метода «Подбор параметра»

Задача. Найти в электронных таблицах корень уравнения приближенным методами (графическим и численным).

Цель работы. Научиться в электронных таблицах при­ ближенно решать уравнения графическим методом и мето­ дом подбора параметра.

Задание 1. В электронных таблицах грубо приближенно графическим методом решить уравнение у =

*3адание 2. Уточнить значения корней уравнения мето­ дом Подбор параметра.

Приближенное решение уравнения графическим методом

1. Запустить электронные таблицы OpenOffice Calc коман­ дой [Программы- OpenOffice -Электронные таблицы].

2. Представим функцию у = в форме табли­ цы значений.

— В диапазон ячеек В1: J 1 ввести значения ар­гумента функции от -4,0 до 4,0 с шагом 1.

— В ячейку В2 ввести формулу для вычисления значений
функции (см рис.) и скопируем ее в диапазон яче­ ек В2: J 2 .

Для грубо приближенного определения корней уравне­ ния построить диаграмму типа График.

Построим график функции.

3. Ввести команду [Вставка- Диаграмма. ] и с помощью Мастера диаграмм постро­ ить диаграмму типа гра­ фик.

Приближенно можно опре­ делить, что график пересекает ось X в точках с координатами -2 и 2, т. е. уравнение имеет корни

Приближенное решение уравнения методом Подбор параметра

Для более точного приближенного решения уравнения методом Подбор параметра сначала необходимо установить требуемую точность представления чисел в ячейках (напри­мер, до 0,001).

1. Ввести команду [Формат — Формам ячеек. ].

В появившемся диалоговом окне Формат ячеек вы­ брать вкладку Число.

С помощью счетчика Число десятичных знаков установить необходимое количе­ ство знаков после запятой.

Для приближенного решения уравнения с использова­нием метода Подбор параметра сначала необходимо вы­брать ячейку, в которой первое значение функции y наибо­ лее близко к нулю.

Таким значением является -0,4 в ячейке D 2. Выделить эту
ячейку и ввести команду [Данные – Анализ «что если» — Подбор параметра].

На панели Подбор параметра в поле Значение ввести
требуемое значение функции (в данном случае 0).

В поле Изменяемая ячейка ввести адрес ячейки $ D $1, в которой будет производиться подбор значения аргу­ мента. Щелкнуть по кнопке Да.

4. На панели OpenOffice . org Calc будет выведена инфор­мация о величине подобран­ ного значения функции. Щелкнуть по кнопке Да.

5. В ячейке аргумента D 1 появится подобранное значение
корня с заданной точностью -2,093.

Для уточнения значения второго корня уравнения мето­дом Подбор параметра сначала необходимо выбрать ячей­ ку, в которой второе значение функции у наиболее близко к нулю.

Таким значением является -1,4 в ячейке Н2. Выделить
ячейку, ввести команду [Данные – Анализ «что если» — Подбор параметра]. и повторить пункты 3 — 4.

В ячейке аргумента H 1 появится подобранное значение
второго корня 2,349.

Таким образом, корни уравнения х ₁

2,349 найдены с точностью представления чисел в ячейках таблицы.

Задания для самостоятельного выполнения

Практическое задание. В электронных таблицах приближенно решить уравнение х — sinx = 0 графически и с помощью метода Подбор параметра.

2. Практическое задание. В электронных таблицах приближенно решить уравнение х — cosx = 0 графически и с помощью мето­ да Подбор параметра

Краткое описание документа:

Тема «Моделирование и формализация». Урок «Приближенное решение уравнений»

Практическая работа : «Приближенное решение уравнений графическим методом и с помощью метода «Подбор параметра».

Данную работу можно использовать при изучении темы «Моделирование и формализация».

Практическая работа из учебника «Информатика. 9 класс» Угринович Н.Д.