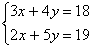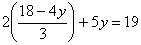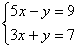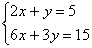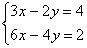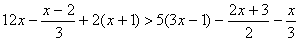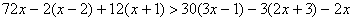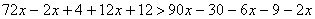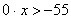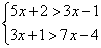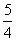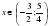Практическая работа решение линейных уравнений

Практическая работа № 7 по учебной дисциплине ЕН.01 Математика
учебно-методический материал на тему

Практическая работа № 7 Решение систем линейных алгебраических уравнений

задания к работе

1 Методом Крамера найти решение системы линейных алгебраических уравнений.

2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.

4. Найти общее решение однородной системы линейных алгебраических уравнений.

В работе имеется Образец решения варианта.

Скачать:

Предварительный просмотр:

Практическая работа № 7

Решение систем линейных алгебраических уравнений

Задание к работе

1. Методом Крамера найти решение системы линейных алгебраических уравнений.

2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.

4. Найти общее решение однородной системы линейных алгебраических уравнений.

Образец решения варианта.

1. Методом Крамера найти решение системы линейных алгебраических уравнений

Решение системы находим по формулам Крамера

Вычислим определитель системы

Последовательно заменив в , первый, второй и третий столбцы столбцом свободных членов, получим соответственно

2. Дана система из трех уравнений с тремя неизвестными. Установить, что система уравнений имеет единственное решение и найти его с помощью обратной матрицы

Если определитель системы отличен от нуля, то система имеет единственное решение (теорема Крамера).

Вычислим определитель данной системы :

следовательно, система имеет единственное решение.

Данную систему можно записать в матричной форме :

, где , , .

Так как , то для матрицы существует обратная матрица . Умножив матричное уравнение слева на , получим , откуда , или .

Найдем обратную матрицу по формуле

где алгебраическое дополнение элемента .

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений

Выпишем расширенную матрицу данной системы и приведем ее к ступенчатому виду

Последовательно умножим первую строку на (–2) и прибавим ее ко второй строке, затем умножим на (–3) и прибавим к третьей строке, умножим на (–2) и прибавим к четвертой строке, получим

Ко второй строке полученной матрицы прибавим третью строку, умноженную на , затем во вновь полученной матрице умножим третью строку на , четвертую – на (–1), затем последовательно умножим вторую строку на 2 и прибавим ее к третьей строке, умножим на 7 и прибавим к четвертой строке, получим

Третью строку полученной матрицы умножим на , четвертую – на , затем третью строку умножим на (–1) и прибавим к четвертой строке, получим

Найденная матрица имеет треугольный вид; по этой матрице запишем систему уравнений, эквивалентную исходной системе,

Последовательно находим неизвестные, начиная с последнего уравнения, ; подставим в третье уравнение найденное , вычислим , ; затем из второго уравнения находим , ; из первого уравнения получим , .

4. Найти общее решение однородной системы линейных алгебраических уравнений .

Элементарными преобразованиями строк приведем матрицу системы к эквивалентной матрице , которой соответствует уравнение , эквивалентное исходной системе. Таким образом, общее решение может быть записано в форме , или , . Решений бесчисленное множество – любая пара, связанная указанной зависимостью, обращает левые части уравнений данной системы в нуль. В системе — число неизвестных и число уравнений. , матрица системы, расширенная матрица системы. В силу теоремы Кронекера-Капелли система имеет бесчисленное множество решений, зависящих от одного параметра . Иногда общее решение удобнее использовать в форме

Практическая работа № 7

Решение систем линейных алгебраических уравнений

1. Методом Крамера найти решение системы линейных алгебраических уравнений.

2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.

4. Найти общее решение однородной системы линейных алгебраических уравнений

3.3 3.4

Практическая работа № 7

Решение систем линейных алгебраических уравнений

1. Методом Крамера найти решение системы линейных алгебраических уравнений.

2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.

4. Найти общее решение однородной системы линейных алгебраических уравнений

5.1 5.2

«Решение линейных уравнений, систем уравнений и неравенств»

Разработка содержит практическую работу по теме «Решение линейных уравнений,систем уравнений и неравенств» для обучающихся СПО и НПО.Проводится при повторении основного материала.

Содержимое разработки

Практическая работа по теме: «Решение линейных уравнений, систем уравнений и неравенств»

Повторить знания обучающихся в теме: « Решение линейных уравнений, систем уравнений и неравенств».

Закрепить умения и навыки решения линейных уравнений, систем уравнений и неравенств .

Определить уровень усвоения знаний, оценить результат деятельности обучающихся.

Оборудование: рабочие тетради и тетради для практических работ, ручка, калькулятор.

Продолжительность: 1 час

Ознакомиться с теоретическим материалом и решением примеров .

Сделать краткий конспект теоретического материала в рабочих тетрадях (основные понятия, определения, формулы, примеры).

В тетрадях для практических работ выполнить практическую работу .

Линейные уравнения.
Уравнение вида ax+ b=0, где a и b — некоторые постоянные, называется линейным уравнением.
Если a  0, то линейное уравнение имеет единственный корень: x = .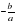
Если a=0; b  0, то линейное уравнение решений не имеет.
Если a=0; b = 0, то, переписав исходное уравнение в виде ax = -b, легко видеть, что любое x является решением линейного уравнения.
Решить уравнение — значит найти все его корни или доказать, что корней нет.
При решении уравнений используются следующие свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Примеры решения уравнений

2x – 3 + 4(x – 1) = 5

Пос Последовательно раскроем скобки, приведём

подобные члены и найдём x:

2x – 3 + 4x – 4 = 5

2x + 4x = 5 + 4 + 3,
6x = 12

Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим:
16х-15х=88-40-12

2x – 3 + 2(x – 1) = 4(x – 1) – 7

2x + 2x – 4x = 3 +2 – 4 – 7

2x + 3 – 6(x – 1) = 4(x – 1)+ 5

2x – 6x + 3 + 6 = 4 – 4x + 5
– 4x + 9 = 9 – 4x
-4x + 4x = 9 – 9
0x = 0 Ответ: Любое число.

Системы уравнений с двумя переменными
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему — значит найти все ее решения или доказать, что их нет.
При решении линейных систем используют метод подстановки и метод сложения.

Примеры решения систем уравнений

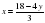
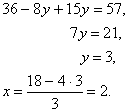
Для решения этой системы применим метод подстановки . Выразим из первого уравнения х и подставим это значение во второе уравнение системы, получим :

Ответ: (2; 3).

Для решения этой системы применим метод сложения уравнений . 8х=16, х=2. Подставим значение х=2 в первое уравнение, получим 10-у=9, у=1.
Ответ: (2; 1).

Эта система равносильна одному уравнению 2х+у=5, т.к. второе уравнение получается из первого умножением на 3. Следовательно, ей удовлетворяет любая пара чисел (х; 5-2х). Система имеет бесконечное множество решений.
Ответ: (х; 5-2х), х–любое.

Умножим первое уравнение на –2 и сложим

С со вторым уравнением, получим 0×х+0×у=-6. Этому у уравнению не удовлетворяет ни одна пара чисел. Сл Следовательно, эта система не имеет решений.
Ответ: система не имеет решений.

Линейные неравенства с одной переменной .

Линейным называется неравенство вида ax+b0 (соответственно ax+b 0, ax+b 0), где а и b – действительные числа, причем а0.
Неравенства решаются на основе следующих утверждений.
Теорема 1. Если какой-либо член неравенства с одной переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.

Примеры решения неравенств

2(х-3)+5(1-х) 3(2х-5)

Раскрыв скобки, получим 2х-6+5-5х6х-15
-3х-1 6х-15

-9х -14

Ответ: .

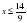
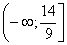
Освободимся от знаменателей, для чего умножим обе части неравенства на положительное число 6, оставив без изменения знак неравенства:

Далее последовательно получаем:

Последнее неравенство верно при любом значении х, так как при любом значении переменной получается истинное

высказывание 0-55. Поэтому множеством его решений служит вся числовая прямая.
Ответ:

Система неравенств
Говорят, что несколько неравенств с одной переменной образуют систему, если ставится задача найти множество общих решений заданных неравенств.
Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.
Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих систему. Неравенства, образующие систему, объединяются фигурной скобкой.

Пример решения систем неравенств

x

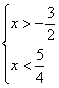
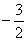
С помощью числовой прямой находим, что пересечением этих множеств служит интервал 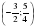. Ответ:

Практическая работа по теме «Решение линейных уравнений. Решение систем линейных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема. Решение линейных уравнений. Решение систем линейных уравнений

Цель: отработать навыки решения линейных уравнений, систем линейных уравнений по алгоритму.

Продолжительность занятия: 2 часа.

Оснащение: методические указания для проведения практических занятий (карточки – задания).

Методические указания по выполнению работы: изучить краткие теоретические и учебно-методические материалы по теме практического занятия; изучить условие задания практического занятия; при выполнении работы соблюдать последовательность действий, ответить на контрольные вопросы; оформить отчет по практической работе.

Порядок выполнения работы:

Равенство — это два выражения, соединенные знаком равенства («=»).

Равенство, верное при всех значениях входящих в него букв, называется тождеством.

Равенство, содержащее букву, значение которой нужно найти, называется уравнением.

Значение буквы, при котором уравнение превращается в верное равенство, называется решением или корнем уравнения.

Решить уравнение — это значит найти все его решения или показать, что уравнение решений не имеет.

Линейным уравнением с одним неизвестным называется уравнение вида:

ax + b = 0, где a и b – известные действительные числа, а x – неизвестная величина.

Для линейного уравнения ax + b = 0 могут представиться три случая:

Если a ≠ 0, то решение (корень) уравнения имеет вид: .

Если a = 0, b = 0, тогда 0 · x + 0 = 0. Здесь x может быть любым числом.

Если a = 0, b ≠ 0, тогда 0 · x + b = 0. Здесь нет решений.

Многие уравнения в результате преобразований сводятся к линейным.

Общий порядок решения задач с помощью уравнений:

1). Ввести переменные, т. е. буквами x , y , z обозначают неизвестные величины, которые либо требуется найти в задаче, либо они необходимы для отыскания искомых величин.

2). С помощью введённых переменных и данных в задаче чисел и их соотношений составить уравнение (или систему уравнений).

3). Решить составленное уравнение (или систему уравнений) и из полученных решений отбирают те, которые подходят по смыслу задачи.

4). Если буквами x , y , z обозначили не искомые величины, то с помощью полученных решений находят ответ на вопрос задачи.

Системы двух линейных уравнений с двумя неизвестными имеют вид:

Методы решения систем уравнений:

1). Метод подстановки.

Из одного уравнения выражаем одно из неизвестных, например x, через коэффициенты и другое неизвестное y:

2) Подставляем во второе уравнение вместо x:

3) Решая последнее уравнение, находим y:

4) Подставляем это значение вместо y в выражение (2):

2). Сложение или вычитание.

Умножаем обе части 1-го уравнения системы (1) на (– а ₂₁ ), а обе части 2-го уравнения на а ₁₁ и складываем их:

2) Подставляем найденное для y значение в любое уравнение системы (1):

3) Находим другое неизвестное:

Таким образом, формулы для решения системы двух линейных уравнений с двумя неизвестными имеют вид:

3). Правило Крамера.

Матрицей называется прямоугольная таблица чисел или буквенных выражений, содержащая m строк и n столбцов:

,

a _ij называют элементами матрицы.

Квадратной матрице А порядка n можно сопоставить число detA (или, или Δ ), называемое её определителем, следующим образом:

Используя определители, можно переписать формулы (3):

Формулы (4) называются правилом Крамера для системы двух линейных уравнений с двумя неизвестными.

Исследование решений системы двух линейных уравнений с двумя неизвестными, показывает, что в зависимости от коэффициентов уравнений возможны три различных случая:

коэффициенты при неизвестных не пропорциональны: ,

в этом случае система линейных уравнений имеет единственное решение , получаемое по формулам (4);

все коэффициенты уравнений пропорциональны: ,

в этом случае система линейных уравнений имеет бесконечное множество решений , так как здесь мы имеем фактически одно уравнение вместо двух.

коэффициенты при неизвестных пропорциональны, но не пропорциональны

свободным членам: , в этом случае система линейных уравнений не имеет решений , так как мы имеем противоречивые уравнения.

Образец решения задач

Пример1 . Решить систему уравнений:

Из первого уравнения выразим х через коэффициенты и y:

Подставляем это выражение во второе уравнение и находим y:

( 2y + 4 ) / 3 + 3y = 5 , откуда y = 1 .

Теперь находим х, подставляя найденное значение вместо y в выражение для х: x = ( 2 · 1 + 4 ) / 3, откуда x = 2 .

Пример 2 . Решить систему уравнений методом сложения или вычитания:

Умножаем первое уравнение на –1, второе – на 3 и складываем их:

отсюда y = 1. Подставляем это значение во второе уравнение: 3x + 9 = 15, отсюда x = 2.

Пример 3. Найдите определители:

Пример 4 . Решить систему уравнений, используя правило Крамера.

1). Является ли число — 1,5 корнем уравнения:

2). Является ли уравнение линейным:

3). Решите уравнение:

4). Решите уравнение: 11(х-4)+10(8-3х)=4+3(4-3х).

5). Решите уравнение: 3(2у+1)-4(1-3у)-5(6у-7)=16.

6). При каком значении переменной х значение выражения 4(5-2х)+36 равно 2х?

7) При каком значении переменной х значение выражения 5(4х-9) на 39 больше значения выражения 6х?

8) При каком значении переменной х значение выражения 5х-7 на 6 больше значения выражения 8-2х?

9) При каком значении переменной х значение выражения 3(2х-4)+5х-(28+х) равно 0?

10) Решите задачу с помощью уравнения: «Одно число в 4 раза больше другого. Найдите эти числа, если их разность равна 81».

11) Студент задумал число. Затем увеличил его втрое и к полученному результату прибавил 21. У него получилось 72. Найдите задуманное число.

12) Сумма трёх последовательных целых чисел равна 144. Найдите эти числа.

13) На трёх полках лежит 66 книг, причём на нижней полке втрое больше, а на средней вдвое больше, чем на верхней. Сколько книг на каждой полке?

14) В первом баке бензина втрое больше, чем во втором. Если перелить из первого бака во второй 25 л бензина, то в баках бензина будет поровну. Сколько литров бензина в первом баке?

15). Решите систему уравнений способом сложения:

16). Решите систему уравнений способом подстановки:

а)

17). Решите систему уравнений:

18). Решите систему уравнений:

19). Решите систему уравнений:

Сформулируйте определение уравнения.

Что значит решить уравнение?

Что называется линейным уравнением с одним неизвестным?

Перечислите основные методы решения систем двух линейных уравнений с двумя неизвестными.

Что называется матрицей?

Что называется определителем второго порядка?

Что называется определителем третьего порядка?

Попов, А.М. Информатика и математика: учебник и практикум для СПО / А.М. Попов, В.Н. Сотников, Е.И. Нагаева, М.Л. Акимов; под ред. А.М. Попова. – 2-е изд., перераб.и доп. – М.: Юрайт, 2015. – 509 с. – Проф. образование.

Шипачев, В.С. Математика: учебник и практикум для СПО / В.С. Шипачев; под ред. А.Н. Тихонова. – 8-е изд., перераб. и доп. – М.: Юрайт, 2014. – 447 с. – Проф. образование.