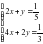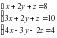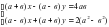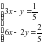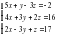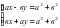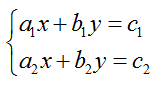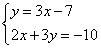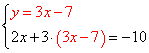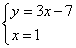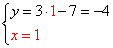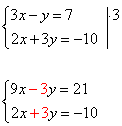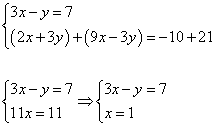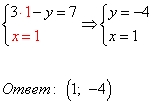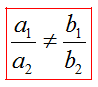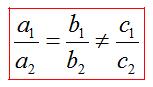Практическая работа система уравнений математика

Практическая работа № 7 по учебной дисциплине ЕН.01 Математика
учебно-методический материал на тему

Практическая работа № 7 Решение систем линейных алгебраических уравнений

задания к работе

1 Методом Крамера найти решение системы линейных алгебраических уравнений.

2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.

4. Найти общее решение однородной системы линейных алгебраических уравнений.

В работе имеется Образец решения варианта.

Скачать:

Предварительный просмотр:

Практическая работа № 7

Решение систем линейных алгебраических уравнений

Задание к работе

1. Методом Крамера найти решение системы линейных алгебраических уравнений.

2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.

4. Найти общее решение однородной системы линейных алгебраических уравнений.

Образец решения варианта.

1. Методом Крамера найти решение системы линейных алгебраических уравнений

Решение системы находим по формулам Крамера

Вычислим определитель системы

Последовательно заменив в , первый, второй и третий столбцы столбцом свободных членов, получим соответственно

2. Дана система из трех уравнений с тремя неизвестными. Установить, что система уравнений имеет единственное решение и найти его с помощью обратной матрицы

Если определитель системы отличен от нуля, то система имеет единственное решение (теорема Крамера).

Вычислим определитель данной системы :

следовательно, система имеет единственное решение.

Данную систему можно записать в матричной форме :

, где , , .

Так как , то для матрицы существует обратная матрица . Умножив матричное уравнение слева на , получим , откуда , или .

Найдем обратную матрицу по формуле

где алгебраическое дополнение элемента .

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений

Выпишем расширенную матрицу данной системы и приведем ее к ступенчатому виду

Последовательно умножим первую строку на (–2) и прибавим ее ко второй строке, затем умножим на (–3) и прибавим к третьей строке, умножим на (–2) и прибавим к четвертой строке, получим

Ко второй строке полученной матрицы прибавим третью строку, умноженную на , затем во вновь полученной матрице умножим третью строку на , четвертую – на (–1), затем последовательно умножим вторую строку на 2 и прибавим ее к третьей строке, умножим на 7 и прибавим к четвертой строке, получим

Третью строку полученной матрицы умножим на , четвертую – на , затем третью строку умножим на (–1) и прибавим к четвертой строке, получим

Найденная матрица имеет треугольный вид; по этой матрице запишем систему уравнений, эквивалентную исходной системе,

Последовательно находим неизвестные, начиная с последнего уравнения, ; подставим в третье уравнение найденное , вычислим , ; затем из второго уравнения находим , ; из первого уравнения получим , .

4. Найти общее решение однородной системы линейных алгебраических уравнений .

Элементарными преобразованиями строк приведем матрицу системы к эквивалентной матрице , которой соответствует уравнение , эквивалентное исходной системе. Таким образом, общее решение может быть записано в форме , или , . Решений бесчисленное множество – любая пара, связанная указанной зависимостью, обращает левые части уравнений данной системы в нуль. В системе — число неизвестных и число уравнений. , матрица системы, расширенная матрица системы. В силу теоремы Кронекера-Капелли система имеет бесчисленное множество решений, зависящих от одного параметра . Иногда общее решение удобнее использовать в форме

Практическая работа № 7

Решение систем линейных алгебраических уравнений

1. Методом Крамера найти решение системы линейных алгебраических уравнений.

2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.

4. Найти общее решение однородной системы линейных алгебраических уравнений

3.3 3.4

Практическая работа № 7

Решение систем линейных алгебраических уравнений

1. Методом Крамера найти решение системы линейных алгебраических уравнений.

2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.

4. Найти общее решение однородной системы линейных алгебраических уравнений

5.1 5.2

Практическая работа по математике с методическими рекомендациями. Тема: «Решение систем линейных уравнений»»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Практическая работа №3

Тема: «Решение систем линейных уравнений»

Цель: сформировать умение исследовать и использовать различные методы для решения систем линейных алгебраических уравнений

Методические указания и теоретические сведения к практической работе

1. Системы линейных уравнений

Пусть задана система линейных уравнений с неизвестными

(1)

Решением системы (1) называется совокупность чисел ( , , …, ), которая при подстановке в систему (1) вместо неизвестных обращает каждое уравнение системы в тождество. Система может иметь решение, тогда она называется совместной , причем, если решение единственное, система определенная , если решений множество – система неопределенная . Если система не имеет решений, она называется несовместной . Рассмотрим два способа решения системы: метод Крамера и метод Гаусса.

При решении методом Крамера используем определители -го порядка. Пусть задана система (1). Составим главный определитель системы из коэффициентов при неизвестных:

.

ТЕОРЕМА. Если определитель системы , то систему (3) можно решить по формуле Крамера, причем это решение единственное:

; ; … ; ,

где определитель может быть получен из главного определителя путем замены -го столбца на столбец из свободных членов.

Составляем главный определитель, элементами которого являются коэффициенты при неизвестных:

и три вспомогательных определителя:

; ; .

Определитель составлен из определителя путем замены элементов первого столбца свободными членами системы уравнений. В определителях и соответственно второй и третий столбцы заменены свободными членами. Вычислим все четыре определителя.

;

;

;

.

Неизвестные , , находим по формулам

; ; ;

; ; .

Ответ: ; ; .

Пример2. Решить систему методом Крамера.

Решение. Выписываем A — матрицу системы и B — столбец свободных членов: , . Далее вычисляем определители:

;

;

;

.

По теореме Крамера ; ; . Ответ: ; ; .

Для проверки результата подставим полученные значения неизвестных в каждое уравнение системы: , , . Все уравнения обратились в тождества, значит, решение найдено верно.

Условия неопределенности и несовместности системы двух линейных уравнений с двумя переменными.

Если определитель системы , то система является либо несовместной (когда и ), либо неопределенной (когда и ). В последнем случае система сводится к одному уравнению, а другое является следствием этого уравнения.

Условия несовместности системы двух линейных уравнений с двумя переменными можно записать в виде:

Условия неопределенности системы двух линейных уравнений с двумя переменными можно записать в виде:

Если один из вспомогательных определителей отличен от нуля, то система уравнений (1) не имеет решения (если ).

Если главный и все вспомогательные определители равны нулю, то система (1) имеет бесконечно много решений.

Если главный определитель отличен от нуля, то система уравнений (1) имеет единственное решение.

Эффективным методом решения и исследования систем линейных уравнений является метод последовательного исключения неизвестных, или метод Гаусса.

Идея метода Гаусса состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему специального вида, которая легко исследуется и решается.

.

В результате элементарных преобразований добиваются того, чтобы в последнем уравнении системы осталось одно неизвестное ( ), во втором – 2 неизвестных ( и ) а в первом – 3 неизвестных ( , , ). За ведущее уравнение берется то, в котором коэффициент при равен 1. Если такого уравнения нет, то его легко получить, разделив любое из уравнений системы на коэффициент при .

Ведущим уравнением данной системы будет последнее. Перепишем систему так:

(2)

Умножаем первое уравнение на (-2) и складываем со вторым, чтобы избавиться от во втором уравнении. Результат сложения записываем на месте второго уравнения. Далее первое уравнение умножаем на (-5) и складываем с третьим, чтобы избавиться от в третьем уравнении. Результат записываем на месте третьего уравнения. Первое уравнение при этом переписываем без изменений. Получим:

(3)

Системы уравнений (2) и (3) эквиваленты, т. е. они обе несовместны, или же обе совместны и имеют одни и те же решения.

Умножаем второе уравнение системы (5) на (-1) и складываем с третьим, чтобы избавиться от в третьем уравнении. Первое уравнение при этом не трогаем. Результат записываем на месте третьего уравнения. Тогда

.

Из последнего уравнения . Подставляем это значение во втрое уравнение системы и находим :

.

В первое уравнение подставляем значения и , получаем

.

Ответ: ; ; .

Рекомендуется сделать проверку.

Систему можно решить и матричным способом.

Рассмотрим систему вида

Составим матрицу системы из коэффициентов при неизвестных:

.

Из неизвестных , , и свободных членов составим матрицы – столбцы

; (5)

Тогда система (4) в матричной форме примет вид

.

Чтобы найти матрицу , умножим (5) на слева.

A

.

Найти обратную матрицу .

Составляем и вычисляем определитель

.

Определитель вычислен по правилу треугольника.

Транспонируем матрицу. Получаем

.

Вычисляем алгебраические дополнения

; ; ; ; ; ; ; ; .

;

Вычисляем . Вычеркиваем первую строку и второй столбец. Составляем определитель второго порядка из оставшихся элементов.

; .

Вычисляем .

Аналогично вычисляем все остальные алгебраические дополнения:

; ; ; ; ; ; .

Составим обратную матрицу

A

A

Решить систему матричным способом

.

Из коэффициентов при неизвестных составим матрицу :

.

Из неизвестных составим матрицу – столбец:

.

Из свободных членов составим матрицу – столбец:

.

Тогда система запишется в виде

.

Получили матричное уравнение. Умножаем обе части этого уравнения на слева. Получаем:

.

Находим обратную матрицу:

; ;

(матрица, составленная из алгебраических дополнений элементов; (обратная матрица).

Умножая обратную матрицу на , получаем матрицу .

.

Отсюда получаем ответ:

; ; .

Сравните решение этой системы с решением метода Гаусса.

Практическая работа №3

Тема: «Решение систем линейных уравнений»

Цель: сформировать умение исследовать и использовать различные методы для решения систем линейных алгебраических уравнений

Содержание практической работы

Задание 1 . Решить систему уравнений по формулам Крамера:

Задание 2 . Решить систему уравнений по формулам Крамера:

Задание 3 . Решить систему уравнений по формулам Крамера:

Задание 4.

а) При каком значении а система не имеет решений?

б) При каком значении а система имеет бесконечно много решений?

Задание 5 . Решить систему уравнений по формулам Крамера, методом Гаусса матричным методом:.

а)

б)

Задание 6 . Решить систему уравнений методом Крамера:

Задание 7 . Решить систему уравнений по формулам Крамера:

Практическая работа по теме: «Решение систем линейных уравнений»

Цель: формирование умений решать системы линейных уравнений разными способами: способом подстановки, способом алгебраического сложения, графическим способом и по формулам Крамера.

Просмотр содержимого документа
«Практическая работа по теме: «Решение систем линейных уравнений»»

Краевое государственное образовательное учреждение среднего профессионального образования «Хабаровский судостроительный колледж»

Специальность: 15.02.08 «Технология машиностроения»

Дисциплина: ЕН.01. «Математика», курс -1

Преподаватель — Михайлова М.Б.

Тема занятия: «Практическая работа: «Решение систем линейных уравнений»

Практическая работа по теме:

«Решение систем линейных уравнений»

Цель: формирование умений решать системы линейных уравнений разными способами: способом подстановки, способом алгебраического сложения, графическим способом и по формулам Крамера.

Решите систему уравнений способами алгебраического сложения, подстановки, графическим и по формулам Крамера:

а) 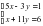б)

Решите систему уравнений по формулам Крамера:

Решите систему уравнений по формулам Крамера:

4. При каком значении а система 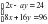имеет бесконечно много решений?

Решите систему уравнений способами алгебраического сложения, подстановки, графическим и по формулам Крамера:

а) 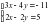б)

Решите систему уравнений по формулам Крамера:

Решите систему уравнений по формулам Крамера:

При каком значении а система 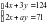не имеет решений?

Методические рекомендации для выполнения

практической работы по теме:

«Решение систем линейных уравнений»

Системы линейных уравнений

Решение системы линейных уравнений способом подстановки

Решение системы линейных уравнений способом сложения

Графическое решение системы линейных уравнений

График линейной функции

1. Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c – числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

2. Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

3. Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера 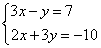методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

4. Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

Ответ: (1; -4).

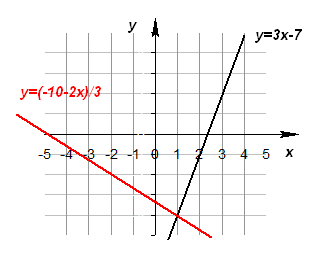
Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система (1)

1) Если , то система (1) имеет единственное решение.

2) Если ,, то система (1) решений не имеет.

В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

.

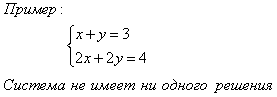
3) Если , то система (1) имеет бесконечное множество решений.

В этом случае прямые совпадают друг с другом.

.

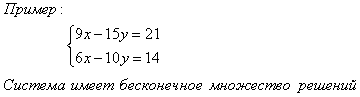
II.Решение систем линейных уравнений по формулам Крамера

Система двух линейных уравнений с двумя переменными

Определитель системы уравнений.

Система трех линейных уравнений с тремя переменными

1.Решение систем линейных уравнений по формулам Крамера

Габриель Крамер (1704–1752) швейцарский математик.

Данный метод применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, то есть ни одно уравнение не являлось бы линейной комбинацией остальных. Для этого необходимо, чтобы определитель системы не равнялся .

Действительно, если какое-либо уравнение системы есть линейная комбинация остальных, то если к элементам какой-либо строки прибавить элементы другой, умноженные на какое-либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.

2.Система из двух уравнений с двумя неизвестными

решается с помощью формул Крамера:

При решении системы возможны три случая:

1. Определитель системы . Тогда система имеет единственное решение, определяемое формулами Крамера.

2. Определитель системы . Если при этом хотя бы один из определителей и не равен нулю, то система не имеет решений.

3. Если , и , то одно из уравнений есть следствие другого, система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений.

П р и м е р 1. Решить систему уравнений .

Решение. Вычислим определитель системы , и дополнительные определители ,

Система имеет единственное решение

П р и м е р 2. Решить систему уравнений .

Решение. Вычислим определитель системы , и дополнитель­ные определители , . Коэффициенты уравнений системы пропорциональны, а свободные члены не подчинены той же пропорции. Система не имеет решений.

Ответ: нет решений.

П р и м е р 3. Решить систему уравнений

Решение. Вычислим определитель системы , и дополнительные определители .

Так как , то одно уравнение есть следствие другого (второе уравнение получено из первого умножением на ).

Система сводится к одному уравнению и имеет бесчисленное множество решений, каждое из которых вычисляется по формуле: , где числовые значения задаются произвольно и вычисляются соответствующие значения .

Ответ: – общее решение данной системы, а решения – частные.

3.Система из трех уравнений с тремя неизвестными

При решении системы из трех уравнений с тремя неизвестными возможны три случая:

1. Определитель системы . Система имеет единственное решение, определяемое формулами Крамера ,

2. Определитель системы равен нулю, . Если при этом хотя бы один из определителей , не равен нулю, то система несовместна, решений не имеет.

3. Если и , то система имеет бесчисленное множество решений.

П р и м е р 4. Решить систему уравнений

Решение. Вычислим определитель системы и дополнительные определители