Практическое применение уравнения бернулли на примере водомера вентури

Применение в технике уравнения Бернулли

Уравнение Бернулли широко применяется в технике, например для расчетов водопроводов, нефтепроводов, газопроводов, насосов и т.п. На его основании сконструирован ряд приборов и устройств, таких как расходомер Вентури, карбюратор, водоструйный насос (эжектор), трубка Пито и т.д.

Измерение скорости потока и расхода жидкости

Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.2.10), загнутый конец которой направлен навстречу потоку.

Трубка полного напора, или трубка Пито , служит для измерения скорости потока, например в трубе. Если установить в одном сечении потока трубку, изогнутую под углом 90, отверстием навстречу потоку и пьезометр, то жидкость в трубке поднимется над уровнем жидкости в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, следовательно, давление увеличивается на величину скоростного напора. Измерив, разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке.

Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

где Н — столб жидкости в трубке Пито.

Рис. 2.10 Трубка Пито и pасходомер Вентури

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.2.10). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Расходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах и осуществляющее сужение потока – дросселирование. Расходомер состоит из двух участков – плавно сужающегося (сопла) и постепенно расширяющегося (диффузора). Скорость потока в сужающемся месте возрастает, а давление падает. Возникает разность (перепад) давлений, которую можно измерить двумя пьезометрами или дифференциальным U-образным ртутным манометром.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

Используя уравнение неразрывности

сделаем замену в получено выражении:

Решая относительно Q, получим

Выражение, стоящее перед , является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

Карбюратор поршневых двигателей внутреннего сгорания (рис.2.11) служит для подсоса бензина и смешивания его с потоком воздуха. Поток воздуха, засасываемого в двигатель, сужается в том месте (сечение 2-2), где установлен распылитель бензина (обрез трубки диаметром d). Скорость воздуха в этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин вытекает в поток воздуха.

Рис. 2.11. Схема карбюратора

Струйный насос (эжектор) (рис.2.12) состоит из плавно сходящегося насадка 2, осуществляющего сжатие потока, и постепенно расширяющейся трубки 4, установленной на некотором расстоянии от насадка в камере 3. Вследствие увеличения скорости потока давление в струе потока на выходе насадка 2 и во всей камере 3 значительно понижается. В расширяющейся трубке 4 скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу). Следовательно, в камере 3 давление обычно меньше атмосферного, т.е. в ней имеется разрежение (вакуум). Под действием разрежения жидкость из нижнего резервуара всасывается по трубе 1 в камеру 3, где происходит слияние и перемешивание двух потоков.

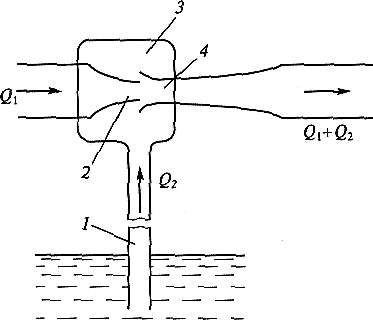
Рис. 2.12. Схема струйного насоса (эжектора):

1 — труба; 2 — насадок; 3 — камера; 4 — расширяющаяся трубка

Курс лекций для специальности 140104 «Промышленная теплоэнергетика» москва 2011

Главная > Контрольные вопросы

Сумма в каждом сечении является пьезометрическим на­пором .

Линия, соединяющая отметки показаний пьезометров, назы­ва­ется пьезометрической линией.

Величина называется скоростным напором

Сумма пьезометрического и скоростного напоров называется гидродинамическим, или полным напором, который можно выразить зависимостью

.

Линия, соединяющая отметки гидродинамических напоров вдоль движения, называется напорной линией, а ее уклон – гидрав­ли­ческим уклоном I.

Величина в уравнении Бернулли представляет потери на­по­ра. Если потери напора отнести к единице длины потока, то полу­чим гидравлический уклон.

В горизонтальных напорных трубках потери напора возникают при уменьшении давления:

– пьезометрический уклон;

– гидравлический уклон.

3.11. Практическое применение уравнения Бернулли

На основе уравнения Бернулли сконструирован ряд приборов, таких, как водомер Вентури, водоструйный насос, эжектор, карбю­ра­торы поршневых двигателей и др.

Примеры

Пример 1 . Водомер Вентури представляет собой короткий от­резок трубы с сужением посредине (рис. 3.13). В широкой части и гор­ловине устанавливаются либо пьезометры, либо дифференциаль­ный манометр.

Применим уравнение Бернулли для сечений 1–1 и 2–2 без учета потерь и при

.

Преобразуем уравнение следующем образом:

.

Согласно (рис. 3.13) разность в левой части равна h .

;

;

.

Используя уравнение расхода , преобразуем формулу к виду

.

Обозначим постоянные величины через – по­стоянная Водомера, тогда – теоретический расход. Дейст­вительный расход водомера определяется по формуле

,

где  – коэффициент расхода водомера.

Пример 2 . Карбюратор поршневых двигателей внутреннего сго­рания служит для осуществления подачи бензина и смешения его с потоком воздуха (рис. 3.14). Поток воздуха, засасываемый в дви­гатель, сужается там, где установлен распылитель бензина.

Скорость воздуха в этом сечении возрастает, а давление по уравнению Бернулли падает.

Найдем соотношение между весовым расходом бензина G б и воздуха G в при заданных размерах D и d и коэффициентах со­про­тив­ления воздушного канала (до сечения 2-2)  в и жиклера ж .

Запишем уравнение Бернулли для потока воздуха (сечения 0–0 и 2–2), а затем для потока бензина (сечения 1–1 и 2–2) и получим при и  = 1.

;

.

.

С учетом весовых расходов

и

.

Пример 3 . Трубка Пито широко применяется для измерения скорости воды и газа. Составим уравнение Бернулли для сечений 1–1 и 2–2. Го­ризонтальная плоскость сравнения 0–0 проходит через носок трубки (рис. 3.15)

.

Так как ; то, обозначив за­пи­шем:

.

.

Контрольные вопросы

1. Напишите уравнение Бернулли для элементарной струйки невязкой жидкости и поясните величины, входящие в него.

2. Чем отличается уравнение Бернулли для потока реальной жидкости от уравнения Бернулли для элементарной струйки?

3. Что называется полной удельной энергией потока?

4. Поясните физический смысл коэффициента Кориолиса в уравнении Бернулли.

5. Поясните энергетический смысл уравнения Бернулли.

6. Что называется пьезометрическим и гидравлическим уклонами?

7. Приведите примеры практического применения уравнения Бер­нулли.

8. На основе какой модели получен вывод уравнения Бернулли для потока реальной жидкости.

9. Что такое пьезометрический и скоростной напор?

Что называется полным напором?

3.12. Гидравлические сопротивления.
Режимы движения жидкости

При движении реальных жидкостей в различных гидросистемах требуется точная оценка потерь напора на преодоление гидрав­ли­ческих сопротивлений. Точный учёт этих потерь во многом оп­ре­деляет надёжность технических расчётов. Кроме того, это позволяет найти экономически целесообразное инженерное решение, об­ладаю­щее достаточной степенью совершенства. Для этого необхо­ди­мо иметь ясное представление о механизме движения жидкости.

В процессе исследований известный физик Рейнольдс в 1883 го­ду подтвердил теорию о существовании двух режимов движения жид­кости. Это прежде всего ламинарный режим движения жид­кости, соответствующий малым скоростям. Ламинарное движение можно рассматривать как движение отдельных слоёв жидкости, происходящее без перемешивания частиц.

При более высоких скоростях движения жидкости наблюдается турбулентный режим («турбулентус» по-латыни – вихревой). Та­кое движение называют беспорядочным.

Для оценки режима движения жидкости Рейнольдс ввёл без­размерный критерий Re, который учитывает влияние скорости v , диаметра (характерного размера) , плотности , а также ди­на­ми­ческой вязкости :

или ,

где  = – кинематическая вязкость.

Граница существования того или иного режима движения жид­кости определяется двумя критическими значениями числа Re: ниж­ним и верхним .

Так, при > Re возможен только ламинарный режим, а при b и h

.

Тогда .

Критерий Рейнольдса является как бы мерой отношения кине­ма­тической энергии жидкости к работе сил вязкого трения. От кри­терия Рейнольдса в общем случае зависят все безразмерные коэф­фи­циенты, входящие в расчётные зависимости, которые приме­ня­ются в практике гидравлических расчётов.

3.13. Потери напора при равномерном движении

Рассмотрим равномерное движение в трубопроводе при следую­щих условиях:

1. Ускорение потока равно нулю, следовательно, силы инерции отсутствуют.

2. Средние скорости во всех поперечных сечениях одинаковы.

3. Местные сопротивления отсутствуют. Существуют сопротив­ле­ния по длине, вызывающие соответствующие потери напора на трение (рис. 3.16).

4. Закон распределения давления между сечениями 1–1 и 2–2 подчиняется гидростатическому, т.е.

.

5. На объём жидкости между сечениями 1–1 и 2–2 действуют силы внешнего давления Р 1 и Р 2 ( Р = р  ), сила тяжести и сила сопротивления движению .

Пользуясь принципом Д’Аламбера, напишем уравнение дина­ми­ческого равновесия для массы жидкости, заключённой между сече­ниями 1–1 и 2–2 на оси х :

. (3.29)

В состав активных сил входят:

1. Сила земного притяжения , проекция которой на ось х равна:

.

Так как , то получаем

. (3.30)

2. С учётом допущения п. 4, равнодействующие сил давления Р 1 и Р 2 приложены в центрах тяжести сечений 1–1 и 2–2 и равны:

и .

Тогда сумма проекций на ось х

. (3.31  )

3. Нормальные силы к оси х равны и противоположно направ-ле­ны, поэтому проекции сил N . N равны нулю.

Очевидно, что левая часть уравнения (3.30) составляет две силы, а именно:

. (3.32)

Силы сопротивления F сопр определяются по касательным напря­жениям на стенке канала. Эти силы направлены параллельно оси потока в сторону, обратную движению жидкости.

Обозначим силу сопротивления на элементарную площадку d  через dF , тогда для участка трубы имеем:

. (3.33)

После интегрирования, принимая ( может изме-няться по периметру) в выражении (3.33), получим

, (3.34)

среднее значение касательного напряжения на стенке.

С учётом уравнений (3.32) и (3.34) запишем уравнение динами­чес­кого равновесия в виде

. (3.35)

Разделив члены уравнения (3.35) на , получим

. (3.36)

Обозначим отношение , после преобразования выражения (3.36), имеем

. (3.37)

Сравним уравнение Бернулли, записанное для сечений 1–1 и 2–2:

. (3.38)

Так как при равномерном движении , то из сопоставления уравнений (3.37) и (3.38) находим

. (3.39)

Учитывая, что (где i – гидравлический уклон), преоб­ра­зуем выражение (3.39) к виду

или . (3.40)

Это уравнение академик Н.Н. Павловский назвал основным урав­нением равномерного движения.

Опытным путём Шези установлено, что величина пропор­цио­нальна квадрату скорости, т.е.

, (3.41)

коэффициент пропорциональности, в общем случае вели­чи­на переменная.

Подставим равенство (3.41) в выражение (3.39), получим фор­мулу Вейсбаха

.

Учитывая, что , преобразуем формулу Вейсбаха к виду

.

Обозначим , получим

, (3.42)

коэффициент гидравлического трения.

Формула (3.42) именуется формулой Дарси-Вейсбаха. Она ис­поль­зуется для расчёта трубопроводов.

Учитывая, что и , получим

.

.

Обозначив , м/с, получим формулу Шези

,

где С – коэффициент Шези.

Формула Шези получила широкое применение в расчётах от­крытых потоков.

Анализ формулы (3.42) показывает, что потери пропор­цио­наль­ны квадрату скорости, а закон сопротивления называется законом квадратичного сопротивления.

В то же время установлено, что потери напора, помимо скорос­ти, зависят от характера режима, формы и размеров сечения, вяз­кос­ти жидкости, материала и состояния стенок.

Это не учитывается формулами Шези и Дарси-Вейсбаха.

На графике (рис. 3.18) показана зависимость потерь на трение в зависимости от скорости движения жидкости . Однако квад­ратичные формулы Шези и Дарси-Вейсбаха очень удобны для практических целей и обычно применяются как для турбулентного, как и для ламинарного режимов течения жидкости.

Отклонения от квадратичного закона учитываются тем, что коэффициенты  и С ставятся в косвенную зависимость от скорости. Поэтому основная задача при определении потерь на трение при равномерном движении жидкости сводится к определению коэф­фи­циентов  и С при известной скорости движения жидкости.

3.14. Способы определения потерь напора
при равномерном движении жидкости

Основной формулой при расчёте напорных трубопроводов явля­е­т­ся формула Дарси-Вейсбаха:

,

а при расчёте течений в открытых руслах – формула Шези:

.

Применение этих формул связано с определением коэффициен­тов  и С .

При ламинарном движении жидкости коэффициент  для труб определяется по формуле

. (3.43)

Впервые наиболее исчерпывающие данные о значении  были получены Никурадзе. Результаты показаны на рис. 3.19.

В пределах прямой 1 коэффициент  зависит не от шерохо­ва­тости стенок трубы, а от числа Re (см. формулу 3.43). Прямая 2 представляет зависимость для гидравлических гладких труб, у которых шероховатость меньше толщины ламинарного при­стенного слоя.

Коэффициент  для гидравлических гладких труб определяется по формуле Блазиуса (прямая 2):

(3.44)

Между линиями 2 и линией 3 слева располагается зона А , в ко­то­рой  зависит как от числа Рейнольдса, так и от шероховатости по­верхности стенок труб.

Для определения  в этой области может применяться формула А. Д. Альтшуля:

, (3.45)

где k э – эквивалентная равномерно зернистая шероховатость, опре­де­ляемая опытным путем.

В области Б коэффициент  зависит только от шероховатости.

Для определения  в этой области рекомендуется формула Никурадзе

, (3.46)

абсолютная шероховатость стенок трубы.

Сущеструют формулы Ф. А. Шевелёва, Н. З. Френкеля, Л. А. Тепакса, Б. Н. Шифринсона, Н. Ф. Фёдорова и других.

3.15. Местные гидравлические сопротивления

Местные сопротивления вызываются фасонными частями, ар­ма­турой и другими элементами трубопровода. При движении жид­кости на местных сопротивлениях изменяется величина и направ­ле­ние скорости.

Потери, связанные с преодолением местных сопротивлений, про­пор­циональны кинетической энергии потока:

, (3.47)

где  м – коэффициент местных сопротивлений зависит не только от вязкости и скорости движения основного потока, но главным образом от геометрической формы и размеров сопротивления.

При турбулентном режиме движения жидкости потери h м зависят только от геометрических характеристик сопротивления.

Рассмотрим вопрос о потере напора при внезапном расширении трубопровода (рис. 3.20). Часть энергии в этом случае расходуется на сложное циркуляционное движение жидкости в кольцевом про­странстве между струёй и стенками трубы за сечением 1–1.

Вследствие отрыва потока и связанного с ним вихреобразования на участке трубы между сечениями 1–1 и 2–2 наблюдаются зна­чи­тельные потери напора.

Учитывая, что давление на торцевой стенке АВ практически равно давлению на выходе из узкой части трубы р 1 , найдём вели­чи­ну потерь по уравнению Бернулли:

(3.48)

Из теоремы импульсов для сечений 1–1 и 2–2 можно записать:

. (3.49)

Пренебрегая силами трения на участке 1–2 и учитывая, что , после деления на обеих частей уравнения (3.49) получим:

. (3.50)

Подставляя выражение (3.50) в уравнение (3.48), найдём:

. (3.51)

То есть, потери напора при внезапном расширении равны ско­рост­ному напору от потерянной скорости. Выражение (3.51) назы­вается теоремой, или формулой Борда.

Формулу (3.51) можно привести к виду:

.

С учётом того, что 1  1 = 2  2 и , получим:

– относится к скорости 1 ;

– относится к скорости 2 .

Суммарные потери напора в трубопроводе постоянного диаметра

.

Примеры

Пример 1 . Определить режим движения жидкости в лотке пря­моугольной формы высотой 0,2 м и шириной 0,5 м при уровне воды 0,15 м и скорости = 1,2 м/c (рис. 3.21).

— Примеры применения уравнения Бернулли

7.5. Примеры применения уравнения Бернулли.

Рассмотрим примеры применения уравнения Бернулли.

1. Расходомер Вентури

Для определения скорости и расхода жидкости часто используется расходомер Вентури. Измерим статическое давление p₁ и p₂ в поперечных сечениях с различными площадями.

Рис. 29

Интеграл Бернулли для сечений 1 и 2 принимает вид

,

.

Рекомендуемые файлы

Из уравнения равенства расходов для двух сечений 1 и 2 имеем

или .

Для вычисления показания дифференциального манометра запишем условие равновесия

.

Собирая все результаты, получаем

.

Формула используется для определения скорости в трубе. Hа практике для повышения точности иногда вводят эмпирический коэффициент, учитывающий гидравлические потери в трубке Вентури.

2. Измерение скорости

Для измерения кинетической энергии используется трубка полного давления, которая устанавливается в точке измерения открытым концом против потока жидкости ( рис. 30 ).

Струйка жидкости, подтекающая к открытому концу трубки, полностью замораживается (v=0) и весь скоростной напор превращается в давление, которое в сумме со статическим достигает давления торможения в данной точке, и называется полным давлением

,

.

Таким образом измерение скорости жидкости или «несжимаемого» газа (M 0, то начинается процесс образования пузырьков пара (кипение), и неразрывность течения капельной жидкости нарушится.

Далее смесь капельной жидкости и пузырьков пара попадает в расширяющийся канал, давление возрастает и пузырьки пара начинают конденсироваться.

Кавитацией называется совокупность процессов образования пузырьков пара и их конденсация.

Кавитация может возникать не только в трубопроводах, но и при внешнем обтекании тел в областях, где возрастают местные скорости и уменьшается давление. Кавитации подвержены быстроходные колеса насосов и турбин, гребные винты.

Конденсация пузырьков пара происходит на твердых поверхностях очень быстро и завершается гидравлическим ударом, при котором развивается местное ударное давление на твердых поверхностях, достигающее сотен и даже тысяч атмосфер. Поэтому кавитация сопровождается тряской, шумом, снижением КПД насосов и турбин, эрозией твердых поверхностей, а иногда и выходом из строя агрегатов.

Обычно работа гидравлических систем в условиях кавитации не достигаются. Для предотвращения кавитации минимальное давление жидкости в системе должно быть больше давления паров, насыщающих пространство.

Одним из способов предотвращения кавитации является снижение температуры жидкости. Это приводит к снижению давления паров, насыщающих пространство.

Например, вода при 373К кипит при давлении, а при 193К —. При кавитации многокомпонентных жидкостей (керосин, бензин и т.д.) вначале вскипают легкие фракции, а затем тяжелые. Конденсация происходит в обратном порядке.

Для оценки возможности возникновения кавитации используется безразмерный критерий — число кавитации

.

Значение, числа кавитации при котором она возникает, называется критическим .

Явление используется в кавитационных регуляторах расхода.

4. Формула Торричелли

Применим интеграл Бернулли для определения скорости истечения тяжелой несжимаемой жидкости из большого открытого сосуда через малое отверстие( рис. 32).

Рис. 32

Здесь S₁— площадь свободной поверхности, S₂ – площадь отверстия, v₁ и v₂ — скорости на поверхности и в отверстии.

Уравнение неразрывности принимает вид

.

Считая движение жидкости установившимся и безвихревым, применим интеграл Бернулли

.

.

Из уравнения неразрывности

,

.

Если отношение мало, то пренебрегая членом, получаем для скорости истечения приближенную формулу Торричелли.

.

Пример. Определить форму сосуда вращения, употребляемого для водяных часов( рис. 33).

Приведем формулы решения задачи

, , ,

,

, или ,

где .

Используя уравнение Бернулли можно объяснить принцип действия :

1) работы струйного насоса, в котором высоконапорный поток G₁ используется для подачи жидкости G₂ из резервуара ( рис. 34).

2) принцип наддува топливного самолетного бака для предотвращения кавитации в топливной системе при полетах на большой высоте ( рис. 35 )

3) причину повышения подъемной силы крыла при заданной картине линий тока ( рис. 36 )

Уменьшение давления в точках, где скорость потока больше, положено в основу водоструйного насоса. Струя воды подается в трубку, открывающуюся в атмосферу, так что на выходе их трубки давление равно атмосферному. В трубке имеется сужение, по которому вода идет с большой скоростью, вследствие чего давление в этом месте оказывается меньше атмосферного. Такое же давление устанавливается и в охватывающей трубку камере насоса, которая сообщается с трубкой через разрыв, имеющийся в узкой части трубки. Подсоединив к камере насоса откачиваемый объект, из него можно откачать воздух (или какой-либо другой газ) до давления порядка 100 мм рт. ст. Откачиваемый воздух захватывается струей воды и уносится в атмосферу.