Практическая работа по математике на тему: «Дифференциальные уравнения»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Практическая работа № 5.
Тема : Решение дифференциальных уравнений I -го и II -го порядка .
Цель : Проверить на практике знание понятия дифференциального уравнения, виды дифференциальных уравнений, умение решать дифференциальные уравнения I и II –го порядков, находить общее и частное решение.
Обеспечение практической работы :
Теоретический материал методической рекомендации к практической работе.
Практические задания по вариантам.
Теоретический материал и примеры решения дифференциальных уравнений.
1. Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную 
2) зависимую переменную 
3) первую производную функции: 
Решить дифференциальное уравнение – это значит, найти множество функций 
Решить дифференциальное уравнение

В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции:
Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».
Следующий этап – интегрирование дифференциального уравнения. Интегрируем обе части:
Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения. То есть, 
Вместо записи 

В данном случае:
Функция представлена в явном виде. Это и есть общее решение.
Множество функций 

Придавая константе 
Найти частное решение дифференциального уравнения 
По условию требуется найти частное решение ДУ, удовлетворяющее начальному условию. Такая постановка вопроса также называется задачей Коши.
Сначала находим общее решение.
Интегрируем уравнение:

Итак, общее решение: 

Необходимо подобрать такое значение константы 

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» двойку:
В общее решение 


Решить дифференциальное уравнение
Решение: Переписываем производную в нужном нам виде:
Переносим второе слагаемое в правую часть со сменой знака:
Переменные разделены, интегрируем обе части:


Решение распишу очень подробно:


Ответ: общий интеграл:
Примечание: общий интеграл любого уравнения можно записать не единственным способом. Таким образом, если у вас не совпал результат с заранее известным ответом, то это еще не значит, что вы неправильно решили уравнение.
Найти частное решение дифференциального уравнения 

Решение: Сначала найдем общее решение. Данное уравнение уже содержит готовые дифференциалы 

Интегрируем уравнение:

общее решение:
Найдем частное решение, соответствующее заданному начальному условию 
Подставляем найденное значение константы 
Ответ: частное решение:
2.Линейные дифференциальные уравнения второго порядка
с постоянными коэффициентами
В теории и практике различают два типа таких уравнений – однородное уравнение и неоднородное уравнение.
Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:



Неоднородное ДУ второго порядка с постоянными коэффициентами и меет вид:





Какая мысль приходит в голову после беглого взгляда? Неоднородное уравнение кажется сложнее. На этот раз первое впечатление не подводит!
Кроме того, чтобы научиться решать неоднородные уравнения необходимо уметь решать однородные уравнения. По этой причине сначала рассмотрим алгоритм решения линейного однородного уравнения второго порядка:
Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:
По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем 
вместо первой производной записываем просто «лямбду»;
вместо функции 

Существуют три варианта развития событий.
Они доказаны в курсе математического анализа, и на практике мы будет использовать готовые формулы.
Характеристическое уравнение имеет два различных действительных корня
Если характеристическое уравнение 





В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например, 
Решить дифференциальное уравнение
Решение: составим и решим характеристическое уравнение:


Ответ: общее решение:
Характеристическое уравнение имеет два кратных действительных корня
Если характеристическое уравнение 




Вместо 

Если оба корня равны нулю 





Решить дифференциальное уравнение
Решение: составим и решим характеристическое уравнение:
Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно невозбранно применить известную школьную формулу сокращенного умножения:
Получены два кратных действительных корня
Ответ: общее решение:
Характеристическое уравнение имеет сопряженные комплексные корни
Если характеристическое уравнение 





Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом:
Если получаются чисто мнимые сопряженные комплексные корни: 
Решить однородное дифференциальное уравнение второго порядка
Решение: Составим и решим характеристическое уравнение:



Ответ: общее решение:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям 

Решение: составим и решим характеристическое уравнение:


Получены два различных действительных корня, поэтому общее решение:
Алгоритм нахождения частного решения следующий:
Сначала используем начальное условие 
Согласно начальному условию, получаем первое уравнение: 
Далее берём наше общее решение 
Используем второе начальное условие 
Согласно второму начальному условию, получаем второе уравнение: 
Составим и решим систему из двух найденных уравнений:
Подставим найденные значения констант 

Ответ: частное решение:
1. Найти общее решение дифференциального уравнения к разделяющимися переменными.
2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.
4. Найти общее решение дифференциального уравнения 2-го порядка.
5. Найти частное решение дифференциального уравнения 2-го порядка.
1. Найти общее решение дифференциального уравнения c разделяющимися переменными.
2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.
4. Найти общее решение дифференциального уравнения 2-го порядка.
5. Найти частное решение дифференциального уравнения 2-го порядка.
1. Найти общее решение дифференциального уравнения c разделяющимися переменными.
2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.
4. Найти общее решение дифференциального уравнения 2-го порядка.
5. Найти частное решение дифференциального уравнения 2-го порядка.
1. Найти общее решение дифференциального уравнения c разделяющимися переменными.
2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.
4. Найти общее решение дифференциального уравнения 2-го порядка.
5. Найти частное решение дифференциального уравнения 2-го порядка.
1. Найти общее решение дифференциального уравнения к разделяющимися переменными.
2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.
4. Найти общее решение дифференциального уравнения 2-го порядка.
5. Найти частное решение дифференциального уравнения 2-го порядка.
1. Найти общее решение дифференциального уравнения к разделяющимися переменными.
2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.
4. Найти общее решение дифференциального уравнения 2-го порядка.
5. Найти частное решение дифференциального уравнения 2-го порядка.
Критерии оценки практической работы обучающихся
Оценка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Оценка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Оценка «3» ставится, если:
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Оценка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет
обязательными умениями по данной теме в полной мере
Оценка «1» ставится, если:
работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Примеры решений задач по дифференциальным уравнениям
Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.
Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.
В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям
Как решить дифференциальное уравнение онлайн?
Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?
У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.
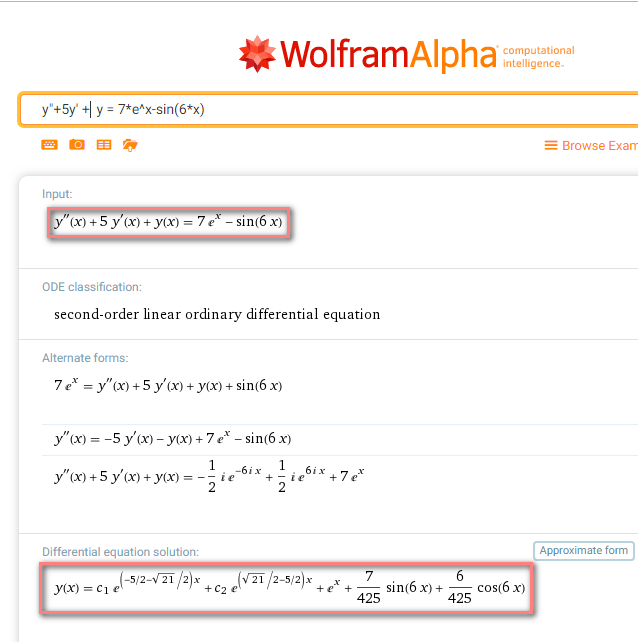
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.
Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.
Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.
Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!
Общий интеграл, семейство кривых
Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$
Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$
Решения дифференциальных уравнений 1 порядка
Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$
Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x \quad (x \ne 0).$
Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$
Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$
Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$
Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$
Решение задачи Коши для ДУ
Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.
Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, \, y(1/3)=1, \, y'(1/3)=2$.
Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= \frac<2y-x><2x+y>, y(1)=1. $$
Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+\cos x, \quad y(0)=0, y'(0)=0, y»(0)=0. $$
Решения дифференциальных уравнений 2 порядка
Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^<2x>.$
Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=\frac<9e^<-3x>><3+e^<-3x>>, \quad y(0)=4\ln 4, y'(0)=3(3\ln 4-1). $$
Cоставление дифференциальных уравнений
Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?
Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.
Решения нелинейных дифференциальных уравнений
Задача 17. Решить дифференциальное уравнение $y^2
Задача 18. Решить дифференциальное уравнение $
Практикум по дифференциальным уравнениям
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
«Нижегородский государственный университет им Н.И. Лобачевского»
ПРАКТИКУМ
по
ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ
Учебное пособие предназначено для студентов, обучающихся по специальности «При-
кладная математика и информатика». Первая часть включает в себя тематику и содержание
практических занятий по дисциплине «Дифференциальные уравнения». Количество предлагаемых
заданий сравнительно невелико; однако все они тщательно подобраны в соответствии с методи-
ческими воззрениями автора и подлежат обязательному выполнению в процессе аудиторных и
домашних занятий. Вторая часть пособия содержит вопросы и задачи для повторения всего кур-
са и может служить проводником и помощником при подготовке к экзамену по дисциплине.
Вопросы носят достаточно развёрнутый характер и в большинстве своём содержат наводящие
на правильный ответ подсказки. Все задачи второй части используются автором в курсе его
лекций по дифференциальным уравнениям в качестве иллюстративного материала.
Часть 1. Практикум.
Раздел 1. Дифференциальные уравнения первого порядка . . . . . . . . . . . . 4
Тема 1. Основные понятия и определения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Тема 2. Метод изоклин . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
Тема 3. Уравнения с разделяющимися переменными . . . . . . . . . . . . . . . . . . . . . .5
Тема 4. Однородные уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6
Тема 5. Линейные уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Тема 6. Уравнения, сводящиеся к линейным . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Тема 7. Уравнения в полных дифференциалах . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Тема 8. Уравнения, не разрешённые относительно производной . . . . . . . . . . . . 9
Тема 9. Особые точки дифференциальных уравнений . . . . . . . . . . . . . . . . . . . 10 Тема 10. Особые решения дифференциальных уравнений . . . . . . . . . . . . . . . . 11
Тема 11. Задачи о траекториях . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Тема 12. Метод последовательных приближений . . . . . . . . . . . . . . . . . . . . . . . . 12
Раздел 2. Дифференциальные уравнения высших порядков . . . . . . . . . .13
Тема 13. Уравнения, допускающие понижение порядка . . . . . . . . . . . . . . . . . . .13
Тема 14. Линейная независимость функций . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14
Тема 15. Линейные уравнения с переменными коэффициентами . . . . . . . . . . 15
Тема 16. Линейные уравнения с постоянными коэффициентами . . . . . . . . . . 16
Тема 17. Уравнения Эйлера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17
Раздел 3. Системы дифференциальных уравнений . . . . . . . . . . . . . . . . . . 18
Тема 18. Системы дифференциальных уравнений . . . . . . . . . . . . . . . . . . . . . . . .18
Тема 19. Метод интегрируемых комбинаций . . . . . . . . . . . . . . . . . . . . . . . . . . . .19
Тема 20. Линейные системы с постоянными коэффициентами . . . . . . . . . . . . 19
Тема 21. Элементы теории устойчивости. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21
Часть 2. Вопросы и задачи для повторения.
Ответы к задачам для повторения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .44
Рекомендуемая литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .51
Часть 1. ПРАКТИКУМ.
Раздел 1. Дифференциальные уравнения
первого порядка.
Тема 1. Основные понятия и определения.
Области единственности решений дифференциального уравнения.
Выделить области, в которых данные уравнения имеют единственные
решения:
1. 


Проверка решений дифференциальных уравнений.
Показать, что данные функции являются решениями указанных диффе-
ренциальных уравнений:
4. 
5. y = 2 + C 
Составление дифференциальных уравнений семейств линий.
Составить дифференциальные уравнения следующих семейств линий:
6. y 2 = 2 Cx + C 2 . 7. y = e x ( ax + b ) . 8. y = C 1 x + 
Тема 2. Метод изоклин.
9. Найти угол α между интегральными линиями уравнений y ‘ = x + y
и y ‘ = x – y в точке М (2;1).
Методом изоклин построить интегральные кривые следующих дифферен-циальных уравнений:
— 4 —
10. y ‘ = 
13. y ‘ = cos ( x – y ).
Тема 3. Уравнения с разделяющимися переменными.
Уравнения с разделяющимися переменными.
Проинтегрировать уравнения:
14. (1 + y 2 ) dx + xy dy = 0. 15. y 2 sin x dx + cos 2 x ln y dy = 0.
16. e — y (1 + y ‘ ) = 1.
Уравнения, приводящиеся с помощью линейной замены
к уравнениям с разделяющимися переменными.
Проинтегрировать уравнения:
17. y’ = ax + by + c ( a, b, c – const ). 18. y ‘ = sin ( x – y ).
Решить задачу Коши для следующих дифференциальных уравнений:
19. y’ sin x – y cos x = 0; y 
20. y’ + sin ( x – y ) = sin ( x + y ); y

2 1. y + xy’ = a (1 + xy ); y
22. x 2 y’ + cos 2 y = 1; y → 
Уравнения, не разрешённые относительно производной.
23. sin y’ = x . 24. e y’ = x .
— 5 —
Геометрические и физические задачи.
25. Найти кривую, обладающую тем свойством, что отрезок касательной
к кривой, заключённый между осями координат, делится в точке касания
пополам.
26. Найти кривую, для которой площадь Q , ограниченная кривой, осью Ox и двумя прямыми Х = 0 , Х = х , является данной функцией от у : Q = a 2 ln 
27. Корабль замедляет своё движение под действием силы сопротивления
воды, которое пропорционально скорости корабля. Начальная скорость кораб-
ля 10 м / с , скорость его через 5 с станет 8 м / с . Когда скорость уменьшится
до 1 м / с ?
28. Пуля входит в доску толщиной h = 10 см со скоростью v 0 = 200 м /с ,
а вылетает из доски, пробив её, со скоростью v 1 = 80 м / c . Считая, что сила сопротивления доски движению пули пропорциональна квадрату скорости
движения, найти время движения пули через доску.
29. По закону Ньютона скорость охлаждения какого-либо тела в воздухе
пропорциональна разности между температурой Т тела и температурой воз-духа Т 0 . Если температура воздуха равна 20 0 С , и тело в течение 20 мин
охлаждается от 100 0 до 60 0 , то через сколько времени его температура по-
низится до 30 0 ?
Тема 4. Однородные уравнения.
30. xy ‘ = y + x cos 2 
Уравнения c правой частью, дробно-линейно зависящей от х и у.

33. 8 x + 4 y + 1 + (4 x + 2 y + 1) y’ = 0. 34. ( y’ + 1) ln 

Обобщённые однородные уравнения.
35. 2 xy’ ( x – y 2 ) + y 3 = 0. 36. ( x + y 3 ) dx + 3( y 3 – x ) y 2 dy = 0.
37. Найти кривую, у которой точка пересечения любой касательной с
осью абсцисс одинаково удалена от точки касания и от начала координат.
38. Найти кривую, для которой произведение абсциссы какой-нибудь точ-
ки на величину отрезка, отсекаемого нормалью на оси Оу , равно удвоенному
квадрату расстояния от этой точки до начала координат.
Тема 5. Линейные уравнения.
Метод вариации произвольной постоянной.
39. xy ‘ – 2 y = x 3 cos x . 40. y ‘ = 
Замена искомой функции произведением.
Проинтегрировать уравнение: 41. y’ x ln x – y = 3 x 3 ln 2 x .
Решить задачу Коши для следующих дифференциальных уравнений:
y’ – y tg x = 

x 2 y’ + y = ( x 2 + 1) e x ; y → 1 при x → — ∞ .
44. Точка массы m движется прямолинейно. На неё действует сила, про-
порциональная времени (коэффициент пропорциональности k 1 ). Кроме того,
точка испытывает сопротивление среды, пропорциональное скорости (коэф-фициент пропорциональности k 2 ). Найти зависимость скорости от времени,
— 7 —
считая, что в начальный момент скорость равна нулю.
45. Найти кривые, обладающие тем свойством, что отрезок, который каса-
тельная в любой точке кривой отсекает на оси Оу , равен квадрату абсциссы
точки касания.
Тема 6. Уравнения, сводящиеся к линейным.
Замена переменной в уравнении Бернулли.
46. y ‘ + 2 xy = 2 xy 2 . 47. ( x 3 + e y ) y ‘ = 3 x 2 .
Замена искомой функции произведением в уравнении Бернулли.
Проинтегрировать уравнение: 48. y’ – y cos x = y 2 cos x .
Метод вариации постоянной при решении уравнения Бернулли.
Проинтегрировать уравнение: 49. y ‘ – 2 ye x = 2 
50. Проинтегрировать уравнение xy ‘ – y 2 + (2 x + 1) y = x 2 + 2 x ,
зная его частное решение y 1 = x .
С помощью замены переменных свести уравнения к линейным и проин-тегрировать их: 51. y ‘ – tg y = e x 

53. С помощью дифференцирования решить уравнение: 
Тема 7. Уравнения в полных дифференциалах.
Уравнения в полных дифференциалах.
Проинтегрировать уравнения:
54. x (2 x 2 + y 2 ) + y ( x 2 + 2 y 2 ) y ‘ = 0.
55. 


Проинтегрировать уравнения:
56. ( x + sin x + sin y ) dx + cos y dy = 0.
57. (2 xy 2 – 3 y 3 ) dx + (7 – 3 xy 2 ) dy = 0.
Зная вид интегрирующего множителя, проинтегрировать уравнения:
58. ( x 2 + y 2 + 1) dx – 2 xy dy = 0; µ = φ ( y 2 – x 2 ).
59. x dx + y dy + x ( x dy – y dx ) = 0; µ = φ ( x 2 + y 2 ).
Тема 8. Уравнения, не разрешённые относительно
производной.
Степенные уравнения относительно производной.
60. x 2 ( y ‘ ) 2 + 3 xyy ‘ + 2 y 2 = 0. 61. ( y’ ) 3 – y ( y’ ) 2 – x 2 y’ + x 2 y = 0.
Уравнение, не содержащее независимой переменной и разрешимое
относительно искомой функции.
62. Проинтегрировать уравнение y ‘ = е 
Уравнение, не содержащее искомой функции и разрешимое
относительно независимой переменной.
63. Проинтегрировать уравнение x ( y ‘ ) 2 = e 
Метод параметризации.
64. Проинтегрировать уравнение у


Общий метод введения параметра.
Проинтегрировать уравнения:
65. y = 2 xy’ + 
Указание. Разрешить уравнение относительно х и дифференцировать по у .
67. Проинтегрировать уравнение: y = x (1 + y ‘ ) + ( y ‘ ) 2 .
Уравнение Клеро.
68. Проинтегрировать уравнение: y = xy ‘ + 
69. Найти кривую, для которой отрезок касательной, заключённый между
координатными осями, имеет постоянную длину а .
Тема 9. Особые точки дифференциальных уравнений.
Особые точки линеаризованных уравнений.
70. Найти и исследовать особые точки данных уравнений. Дать качест-венную картину поведения интегральных кривых:
а) 


г) 

Особые точки нелинеаризованных уравнений.
71. Найти и исследовать особые точки данных уравнений. Дать качест-венную картину поведения интегральных кривых:
— 10 –
а) 


Тема 10. Особые решения дифференциальных уравнений.
Особые точки плоских кривых.
Выяснить характер особых точек кривых: 72. ( у – х 2 ) 2 = х 5 .
73. ( х 2 + у 2 )( х – а ) 2 = b 2 х 2 ( а > 0 , b > 0).
Рассмотреть три случая: 1) а > b ; 2) a = b ; 3) a b .
Огибающие.
74. Найти огибающую семейства окружностей ( х – а ) 2 + у 2 = 
75. Найти кривую, которую огибает отрезок длины l , когда его концы
скользят по осям координат.
76. Найти огибающую эллипсов постоянной площади S , оси симметрии
которых совпадают.
77. Уравнение траектории движения снаряда, выпущенного из точки О
с начальной скоростью v 0 под углом a к горизонту (без учёта сопротивле-ления воздуха), будет у = х tg a — 
той же вертикальной плоскости.
Проинтегрировать уравнения, выделить особые решения и сделать чертёж:
78. ( у ¢ + 1) 3 = 27 ( х + у ) 2 . 79. у 2 ( у ¢ ) 2 – 2 хуу ¢ + 2 у 2 – х 2 = 0.
80. у ( у – 2 ху ¢ ) 2 = 2 у ¢ . 81. ( у ¢ ) 3 = 3( ху ¢ — у ).
Тема 11. Задачи о траекториях.
Найти ортогональные траектории для данных семейств кривых:
82. х 2 – у 2 = а 2 . 83. cos y = ae – x .
84. Найти изогональные траектории для семейства кривых 3 х 2 + у 2 = С,
пересекающие эти кривые под углом j = 30 0 .
Тема 12. Метод последовательных приближений.
Найти три первых последовательных приближения в задаче Коши:
85. у ¢ = х 2 – у 2 ; 

Раздел 2. Дифференциальные уравнения
высших порядков.
Тема 13. Уравнения, допускающие понижение порядка.
Нормальные уравнения с правой частью, зависящей только от х .
Проинтегрировать уравнения:
87. у ¢¢¢ = х + cos x . 88. у ¢¢ ( х + 2) 5 = 1; у (- 1) = 

Уравнения, не содержащие искомой функции и её первых производных.
Проинтегрировать уравнения:
89. у ¢¢¢ = 




Уравнения, не содержащие независимую переменную.
Проинтегрировать уравнения:
91. 3 y ¢ у ¢¢ = 2 у ; у (0) = y ¢(0) = 1.
92. у ¢¢¢ = 3 у y ¢ ; у (0) = y ¢(0) = 1 , у ¢¢(0) = 
Уравнения, однородные относительно искомой функции и её производных.
Проинтегрировать уравнения:
93. хуу ¢¢ — х ( y ¢ ) 2 = у y ¢ . 94. уу ¢¢ = ( y ¢ ) 2 + 15 у 2 
Обобщённые однородные уравнения.
Проинтегрировать уравнения:
95. 4 х 2 у 3 у ¢¢ = х 2 – у 4 . 96. х 2 ( уу ¢¢ — ( y ¢ ) 2 ) + ху y ¢ = (2 х y ¢ — 3 у ) 
Уравнения, обе части которых есть точные производные.
Проинтегрировать уравнения:
97. у ¢¢ + у ¢ cos x – y sin x = 0. 98. 2( у ¢ ) 2 = ( y – 1) у ¢¢ .
Физические и геометрические задачи.
99. Тело массой т падает с некоторой высоты с начальной скоростью
v = 0. При падении тело испытывает сопротивление, пропорциональное квадра-ту скорости ( k – коэффициент пропорциональности). Найти закон падения тела.
100. Найти кривую, проходящую через начало координат и такую, что пло-
щадь треугольника, образованного касательной к кривой в некоторой точке,
ординатой этой точки и осью Ох , пропорциональна площади криволинейной
трапеции, образованной кривой, осью Ох и ординатой этой точки.
Тема 14. Линейная независимость функций.
Исследование системы функций на линейную независимость.
Исследовать, являются ли данные функции линейно независимыми в их
области определения:
101. е х , хе х , х 2 е х . 102. 1 , arcsin x , arccos x .
Найти определитель Вронского для указанных систем функций:
103. 2 , cos x , cos 2 x . 104. 4, sin 2 x , cos 2 x .
Определитель Грама.
С помощью теоремы Грама установить линейную зависимость или неза-
висимость указанных функций на отрезке [ — p ; p ]:
105. 5, cos 2 x , sin 2 x . 106. 1, 2 х, х 2 .
Составление дифференциальных уравнений по заданной
фундаментальной системе решений.
Составить дифференциальные уравнения, для которых данные системы
— 14 –
функций образуют фундаментальные системы решений:
107. у 1 ( х ) = х, у 2 ( х ) = е х . 108. y 1 ( x ) = x, y 2 ( x ) = sin x, y 3 ( x ) = cos x .
109. Доказать правило дифференцирования функционального определителя :
производная по х определителя, составленного из функций от х , равна сумме n определителей, из которых у первого в первой строке функции заменены их производными, а остальные не изменены, у второго во второй строке функции заменены их производными и т.д., у n -го в последней строке функции заменены их производными , то есть

Тема 15. Линейные уравнения с переменными
коэффициентами.
Интегрирование однородных уравнений 2-го порядка с одним
известным частным решением при помощи формулы
Остроградского-Лиувилля.
Найти общие решения данных уравнений, зная их частные решения:
110. ( е х + 1) у ¢¢ — 2 у ¢ — е х у = 0 ; у 1 = е х – 1.
111. у ¢¢ + (tg x – 2 ctg x ) у ¢ + 2 ctg 2 x 
Однородные уравнения с известными частными решениями.
Найти общие решения данных уравнений, зная их частные решения:
112. х 2 (2 х – 1) у ¢¢¢ + (4 х – 3) ху ¢¢ — 2 ху ¢ + 2 у = 0; у 1 = х, у 2 = 
113. ( х 2 – 2 х + 3) у ¢¢¢ — ( х 2 + 1) у ¢¢ + 2 ху ¢ — 2 у = 0; у 1 = х, у 2 =е х .
Неоднородные уравнения с известными частными решениями
соответствующих однородных уравнений.
Проинтегрировать уравнения, если известны частные решения однород-
ных уравнений:
— 15 —
114. х 2 у ¢¢ — ху ¢ — 3 у = 5 х 4 ; у 1 = 
115. (2 х + 1) у ¢¢ + (2 х – 1) у ¢ — 2 у = х 2 + х ;
частное решение однородного уравнения – некоторый многочлен.
Неоднородные уравнения с известными частными решениями.
Найти общие решения данных уравнений, зная их частные решения:
116. ( х 2 – 1) у ¢¢ + 4 ху ¢ + 2 у = 6 х ; у 1 = х, у 2 = 
117. (3 х 3 + х ) у ¢¢ + 2 у ¢ — 6 ху = 4 – 12 х 2 ; у 1 = 2 х, у 2 = ( х + 1) 2 .
Интегрирование неоднородных уравнений методом
вариации постоянных.
Проинтегрировать уравнения:
118. ху ¢¢ — (1 + 2 х 2 ) у ¢ = 4 х 3 е 
119. (1 + х 2 ) у ¢¢ + 2 ху ¢ = 


Тема 16. Линейные уравнения с постоянными
коэффициентами.
Проинтегрировать уравнения:
120. у ¢¢¢ — 3 у ¢¢ + 3 у ¢ — у = 0 ; у (0) = 1 , у ¢(0) = 2 , у ¢¢(0) = 3.
121. у ¢¢¢ + 6 у ¢¢ + 11 у ¢ + 6 у = 0. 122. y VI + 2 y V + y IV = 0.
123. у ¢¢¢ — 8 y = 0. 124. y IV + 4 у ¢¢¢ + 10 у ¢¢ + 12 у ¢ + 5 у = 0.
125. y V + 4 y IV + 5 у ¢¢¢ — 6 у ¢ — 4 у = 0.
Интегрирование неоднородных уравнений методом
вариации постоянных.
Проинтегрировать уравнения:
— 16 —
126. у ¢¢ + 2 у ¢ + 2 у = 

Неоднородные уравнения с квазиполиномиальными правыми частями.
Проинтегрировать уравнения:
128. у ¢¢ + 4 у ¢ + 4 у = 8 е – 2 х . 129. у ¢¢ + у ¢ + у = ( х + х 2 ) е х .
130. у ¢¢ + у = 4 х cos x . 131. у ¢¢ + 2 у ¢ = 4 e x (sin x + cos x ).
132. у ¢¢¢ — у ¢¢ + у ¢ — y = x 2 + x . 133. у ¢¢¢ — 3 у ¢¢ + 3 у ¢ — y = e x cos 2 x .
Принцип суперпозиции.
Проинтегрировать уравнения:
134. у ¢¢ — у ¢ — 2 у = 4 х – 2 е х . 135. y V + 4 у ¢¢¢ = e x + 3 sin 2 x + 1.
136. y IV + 2 у ¢¢¢ + 2 у ¢¢ + 2 у ¢ + у = xe x + 
137. у ¢¢ + у = cos 2 2 x + sin 2 
Тема 17. Уравнения Эйлера.
Проинтегрировать уравнения:
138. х 2 у ¢¢ + 2 ху ¢ + 6 у = 0. 139. (2 х + 1) 2 у ¢¢¢ + 2(2 х + 1) у ¢¢ + у ¢ = 0.
Неоднородные уравнения.
Проинтегрировать уравнения:
140. х 2 у ¢¢ + ху ¢ + у = х (6 – ln x ).
141. х 2 у ¢¢ + 4 ху ¢ + 2 у = 2 ln 2 x + 12 x .


уравнений.
Тема 18. Системы дифференциальных уравнений.
Первые интегралы.
142. Проверить, является ли 143. Проверить, образуют ли равен-
функция y = (1 + х ) е – х – е – у ства < x + y + t = C 1 , x 2 + y 2 + t 2 = C 2 >
интегралом для системы диффе- систему независимых первых интегра-
ренциальных уравнений лов для системы дифференциальных








Метод исключения.
Проинтегрировать системы уравнений:
144. 4 



146. 


147. 

— 18 —
148. 




Нахождение интегрируемых комбинаций.
Проинтегрировать системы уравнений:
149. 







15 1 . 


Системы уравнений в симметрической форме.
Проинтегрировать системы уравнений:
152. 

154. t dx = ( t – 2 x ) dt ,
t dy = ( tx + ty + 2 x – t ) dt .


коэффициентами.
Однородные системы.
Проинтегрировать системы уравнений:
— 19 —
155. 





157. 


Однородные системы, не приведённые к нормальному виду.
Проинтегрировать системы уравнений:
158. 






Метод вариации произвольных постоянных.


160. 




Системы с квазиполиномиальными неоднородностями.
Проинтегрировать системы уравнений:
— 20 —






Тема 21. Элементы теории устойчивости.
Устойчивость по Ляпунову.
164. Исходя из определения устойчивости по Ляпунову, исследовать на устой-
чивость решения следующих уравнений и систем уравнений:
а) 

в) 

Устойчивость по первому приближению.
165. Найти все положения равновесия данных систем и исследовать их на
устойчивость; дать качественную картину поведения интегральных кри-
вых на фазовой плоскости:
а) 




http://www.matburo.ru/ex_ma.php?p1=madiff
http://gigabaza.ru/doc/34375.html