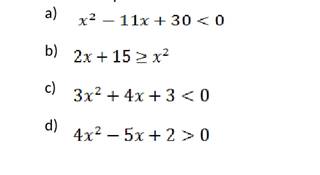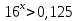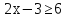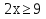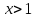Урок- практикум по теме: » Решение показательных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
МБОУ Алексеево-Лозовская СОШ Учитель математики высшей категории Шконда Ирина Андреевна
« Решение показательных уравнений
ШКОНДА ИРИНА АНДРЕЕВНА
по теме « Решение показательных уравнений и неравенств».
Тип урока: Урок обобщения и систематизации знаний по теме: «Показательные уравнения».
-закрепить решение простейших показательных уравнений;
-показать дополнительные методы решения показательных уравнений;
-обобщить и систематизировать методы решения показательных уравнений;
б) развивающие: продолжить работу по развитию умений работать с дополнительной литературой;
-организация совместных действий, ведущих к активизации учебного процесса;
-стимулирование учеников к самооценке образовательной деятельности;
-учащиеся работают над решением проблемы, поставленной учителем;
Оборудование урока: проектор, компьютер, презентация к уроку.
Устная работа по теме урока..
Основная часть .Выступление учеников-практиков по теме.
а) Определение показательного уравнения.
б) Решение показательных уравнений методом уравнивания показателей.
в) Решение показательных уравнений методом вынесения общего множителя за скобки.
г) Решение показательных уравнений способом подстановки.
д) Метод почленного деления.
е) Способ группировки.
ж) Использование графического метода решения уравнений.
з) Решение показательных уравнений методом подбора.
I .Организационный момент. (3 мин)
Учитель формулирует тему и цели урока. Ученики всего класса записывают число и тему урока в тетрадях. Учитель проверяет состав групп, на которые класс был разбит на предыдущем уроке.
II.Устный работа. (5-7минут). Работа в группах.
1.Среди заданных функций укажите те, которые являются показательными: Какие из показательных функций возрастающие, какие, убывающие?
2. Решите уравнения.















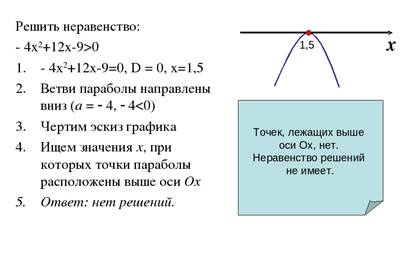
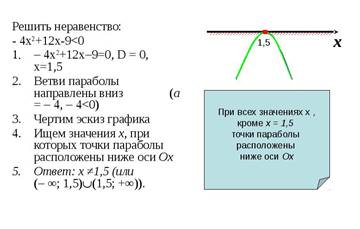
3.Решите неравенства: 
























4. Решите квадратные уравнения по теореме, обратной теореме Виета.















Основная часть урока. Работа по теме урока:
Ученики -практики с помощью презентации домашнего задания показывают теоретические и практические знания решения простейших показательных уравнений. Остальные учащиеся записывают решения в тетрадях.
Задание 1 : Определение показательного уравнения.
Показательное уравнение-это уравнение, содержащее неизвестное в показателе степени.
Основные методы решения показательных уравнений.
Простейшие показательные уравнения вида 
При b 

При b >0 данное уравнение решается логарифмированием обеих частей по основанию a ; 

Пример1. Решите уравнение:
Данное уравнение решений не имеет, т.к. 
Пример 2. Решите уравнение:



Задание 2: Решение показательных уравнений методом уравнивания показателей,
т.е. преобразование данного уравнения к виду а
Пример3. Решите уравнение
Решение. Приведем все степени к одному основанию 0,2. Получим уравнение 



Ответ: 
Задание 3: .Решение показательных уравнений методом вынесения общего множителя за скобки.
Пример1. Решите уравнение 
Решение




Ответ:
Задание 4: Решение показательных уравнений способом подстановки.
С помощью удачной замены переменных некоторые показательные уравнения удается свести к алгебраическому виду, чаще всего к квадратному уравнению.
Пример1. Решите уравнение 









Ответ: 

Задание 5: Метод почленного деления.
Данный метод заключается в том, чтобы разделить каждый член уравнения, содержащий степени с одинаковыми показателями, но разными основаниями, на одну из степеней. Этот метод применяется для решения однородных показательных уравнений.
Пример1.Решите уравнение
Решение: 







Далее имеем: 



Ответ: 

Задание 6: Способ группировки.
Способ группировки заключается в том, чтобы собрать степени с разными основаниями в разных частях уравнения, а затем разделить обе части уравнения на одну из степеней.
Пример1. Решить уравнение.
Решение. Сгруппируем слагаемые следующим образом:




Ответ:
Задание 7: Использование графического метода решения уравнений.
Решить уравнение. 
1). 
2). 
Построим графики и найдем абсциссу точки пересечения. Ответ:
Задание 8: Решение показательных уравнений методом подбора.
При решении показательных уравнений этим методом вначале находят путем подбора корень исходного уравнения, а затем доказывают, что этот корень единственный, с использованием свойства монотонности показательной функции.
Решить уравнение:
Решение: подбором находим, что 



А) Покажем, что среди чисел х.


( 
Ответ:
Закрепление изученного материала.
Каждой группе учащихся в конвертах даются задания. Консультант раздает каждому ученику по одной задаче и через 10 минут решения собираются и сдаются учителю. Затем продолжается обсуждение и решение в группе остальных уравнений.
Решить графическим способом 
Решение: 2 
2.Решить уравнение: (решают в группах).

Решение: поскольку 



Получаем: 







Отсюда 

Проверка и обсуждение заданий:
(10-12 минут) . Готовые решения одного из трех оставшихся заданий записываются на доске каждой группой. Выдвинутый группой ученик объясняет решение, основываясь на теории, выдвигает алгоритм действий. Объяснения длятся около 4 минут. Другие группы могут задать вопросы по решению уравнения.
1)Учитель задает вопросы классу: Какими методами можно решать показательные уравнения?
2) Оценка знаний учащихся : Учитель оценивает деятельность каждой группы. Для выставления отметок за урок раздаются оценочные листы. Предпоследняя колонка заполняется учеником (см. условные обозначения). Консультант заполняет вторую и третью колонки. Учитель ставит итоговые отметки, оценив деятельность всей группы.
Условные знаки для оценивания учеником самого себя :
«+»– отлично изучил тему;
«+;-»– есть проблемы, но я их решил самостоятельно;
«^» – были проблемы, но я их решил с помощью группы;
«-» – проблемы не решены.
5. Домашнее задание:
стр299, №163(б); №164(а);№165(а);№166(а;г); Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений. Под редакцией А.Н. Колмогорова. 13-е издание. Москва «Просвещение»,2003.
Источни ки информации.
Алгебра и начала анализа.10-11 классы: рабочие программы по учебникам Ю.М. Колягина, М.В. Ткачевой, Н.Е. Федоровой, М.И. Шабунина: базовый и профильный уровни/авт.-сост. Н.А. Ким.- Волгоград: Учитель, 2011.
Алгебра и начала математического анализа. 10 класс : учебник для общеобразоват. учреждений : базовый и профильный уровни / Ю. М. Колягин [и др.] ; под ред. А. В. Жижченко. — М. : Просвещение, 2011.
Изучение алгебры и начал математического анализа в 10 классе : книга для учителя / Н. Е. Федорова, М. В. Ткачева. — М.: Просвещение, 2008.
Алгебра и начала математического анализа. 10 класс : дидактические материалы. Углубленный уровень / М. И. Шабунин [и др.]. — М. : Просвещение, 2008.
Тематические тесты. 10 класс : дидактические материалы. Углубленный уровень / М.В. Ткачева [и др.]. — М.: Просвещение, 2009.
Григорьева Г.И. Поурочное планирование по алгебре и началам анализа к учебнику Ш.А. Алимова «Алгебра и начала анализа 10-11 классы». – Волгоград: Учитель, 2009.
Семенов Ф.Л. Ященко И.В.ЕГЭ 3000 задач с ответами Математика с теорией вероятностей и статистикой МИОО 2012-2013 г.
Сборники тестовых заданий ЕГЭ, 2011-2013 Изд. Легион-М, АСТ-Астрель, «Экзамен» и др.
2. Какие из заданных функций являются возрастающими (убывающими)?
А) 


3. Решите уравнения.
А)



5. Решите показательное уравнение методом вынесения общего множителя за скобки.
6. Решить графическим способом
1.Среди заданных функций укажите те, которые являются показательными:
2. Какие из заданных функций являются возрастающими (убывающими)?
А) 


3. Решите уравнения.
А)



4. Решите показательное уравнение способом подстановки
5. Решите показательное уравнение методом вынесения общего множителя за скобки. 
6. Решить графическим способом
1.Среди заданных функций укажите те, которые являются показательными:
2. Какие из заданных функций являются возрастающими (убывающими)?
А) 


3. Решите уравнения.
А)



4. Решите показательное уравнение способом подстановки 
5. Решите показательное уравнение методом вынесения общего множителя за скобки.
6. Решить графическим способом
1.Среди заданных функций укажите те, которые являются показательными:
2. Какие из заданных функций являются возрастающими (убывающими)?
А) 


3. Решите уравнения.
А)



4. Решите показательное уравнение способом подстановки 
5. Решите показательное уравнение методом вынесения общего множителя за скобки. 
6. Решить графическим способом
Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Практическая работа «Показательные неравенства».
Практическое занятие: Показательные неравенства.
Цель: освоить решение показательных неравенств .
1. Для того, чтобы освоить решение показательных неравенств необходимо:
1) знать и уметь решать показательные уравнения;
2) знать и уметь применять признак монотонности (возрастания и убывания) показательной функции;
3) уметь решать простейшие неравенства (линейные, квадратные)
— По первому пункту вы сдали зачёт – решение показательных уравнений освоили.
— По второму пункту мы проводили исследовательскую работу: строили графики показательных функций и обобщили признаки возрастания и убывания функций по их формулам.
— Повторением способов решения простейших линейных и квадратных неравенств,; правил, связанных с решением неравенств, мы будем заниматься сегодня.
2. Познакомьтесь с материалом, вспомните или изучите решение простейших линейных неравенств, сделайте конспект и выполните самостоятельную работу,
Материал для повторения:
1) Изображение, обозначение числовых промежутков.
2) Правила преобразования неравенств, приводящие к равносильным неравенствам.
3). Запишите примеры решения линейных неравенств.
4). Решите самостоятельно неравенства:
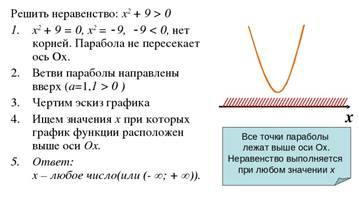
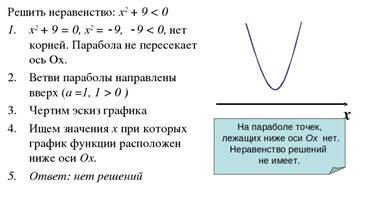
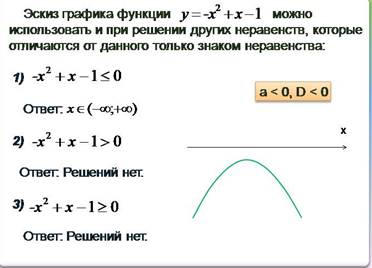
3. Познакомьтесь с материалом, вспомните или изучите решение простейших квадратных неравенств, сделайте конспект и выполните самостоятельную работу.
Материал для повторения:
Решите самостоятельно неравенства:
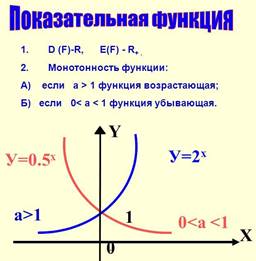
4.Повторите свойство показательных функций на возрастание и убывание (монотонность).
Укажите из перечисленных показательных функций возрастающие и убывающие:
y =( 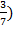
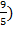
5.Решение показательных неравенств.
Метод приведения к одному основанию.
Пример 1 . Решить неравенство:
Перепишем неравенство: 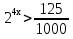
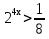
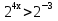
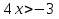
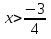
Ответ: х € 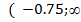
Метод вынесения общего множителя за скобки.
Пример 2. Решить неравенство: 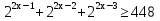
Потому что за скобки выносится наименьшая степень.
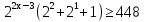
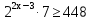
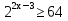
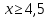
Ответ: 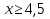
Метод введения новой переменной.
Пример 3. Решить неравенство: 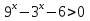
Здесь, как вы видите, лучше использовать Пусть 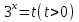
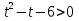
У нас получилось квадратное неравенство.
Для начала найдём корни, т.е. от неравенства перейдём к уравнению: 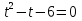
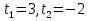
Отмечаем их на числовой прямой, у нас получилось 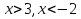
1) Неравенство 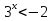
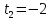
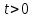
2) 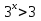
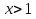
Ответ:
Решите самостоятельно неравенства:
http://www.evkova.org/pokazatelnyie-uravneniya-i-neravenstva
http://znanio.ru/media/prakticheskaya-rabota-pokazatelnye-neravenstva-2666846












































































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);