Предэкспоненциальный множитель в уравнении аррениуса таблица
При фиксированной температуре реакция возможна, если взаимодействующие молекулы обладают определнным запасом энергии. Аррениус эту избыточную энергию назвал энергией активации , а сами молекулы активированными .
По Аррениусу константа скорости и энергия активации связаны соотношением, получившим название уравнения Аррениуса:
| (5.3) |
Здесь – предэкспоненциальный множитель, – универсальная газовая постоянная, – абсолютная температура.
Таким образом, при постоянной температуре скорость реакции определяет . Чем больше , тем меньше число активных молекул и тем медленнее протекает реакция. При уменьшении скорость возрастает, а при = 0 реакция протекает мгновенно.
Величина характеризует природу реагирующих веществ и определяется экспериментально из зависимости . Записав уравнение (5.3) в логарифмическом виде и решая его для констант при двух температурах, находим :
 |
 |
Если = 50–100 кДж∙моль –1 , то из уравнения Аррениуса следует, что при изменении температуры реакции на 10 градусов ее скорость изменится в 2–4 раза. Это правило было эмпирически установленно Вант-Гоффом:
|
 |
γ – температурный коэффициент скорости химической реакции. Правило Вант-Гоффа имеет ограниченное применение, поскольку величина γ зависит от температуры, а вне области = 50–100 кДж ∙ моль –1 это правило вообще не выполняется.
На рис. 5.4 видно, что затрачиваемая на перевод начальных продуктов в активное состояние (А* – активированный комплекс) энергия затем полностью или частично вновь выделяется при переходе к конечным продуктам. Разность энергий начальных и конечных продуктов определяет реакции, которая от энергии активации не зависит.
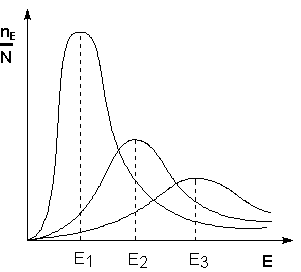
Таким образом, по пути из исходного состояния в конечное система должна преодолеть энергетический барьер. Только активные молекулы, обладающие в момент столкновения необходимым избытком энергии, равным , могут преодолеть этот барьер и вступить в химическое взаимодействие. С ростом температуры увеличивается доля активных молекул в реакционнной среде.
 1 1 | |||||||||||||
| Рисунок 5.4 Предэкспоненциальный множитель характеризует общее число соударений. Для реакций с простыми молекулами близок к теоретической величине столкновений , т. е. , рассчитываемой из кинетической теории газов. Для сложных молекул ≠ , поэтому необходимо вводить стерический фактор :
Стерический фактор учитывает то обстоятельство, что для взаимодействия сложных активных молекул необходима определенная взаимная ориентация: течению процессов способствует столкновение молекул в положениях, когда в соприкосновение приходят их реакционноспособные связи или неподеленные пары электронов. Таким образом, уравнение Аррениуса имеет вид
Здесь – число всех соударений, – доля соударений, благоприятных в пространственном отношении (принимает значения от 0 до Размерность константы скорости получается из соотношения
и, как видно из уравнения Аррениуса, размерность предэкспоненты та же. Для и концентраций, выраженных в моль∙л –1 , имеет следующие приблизительные значения в реакциях различной молекулярности:
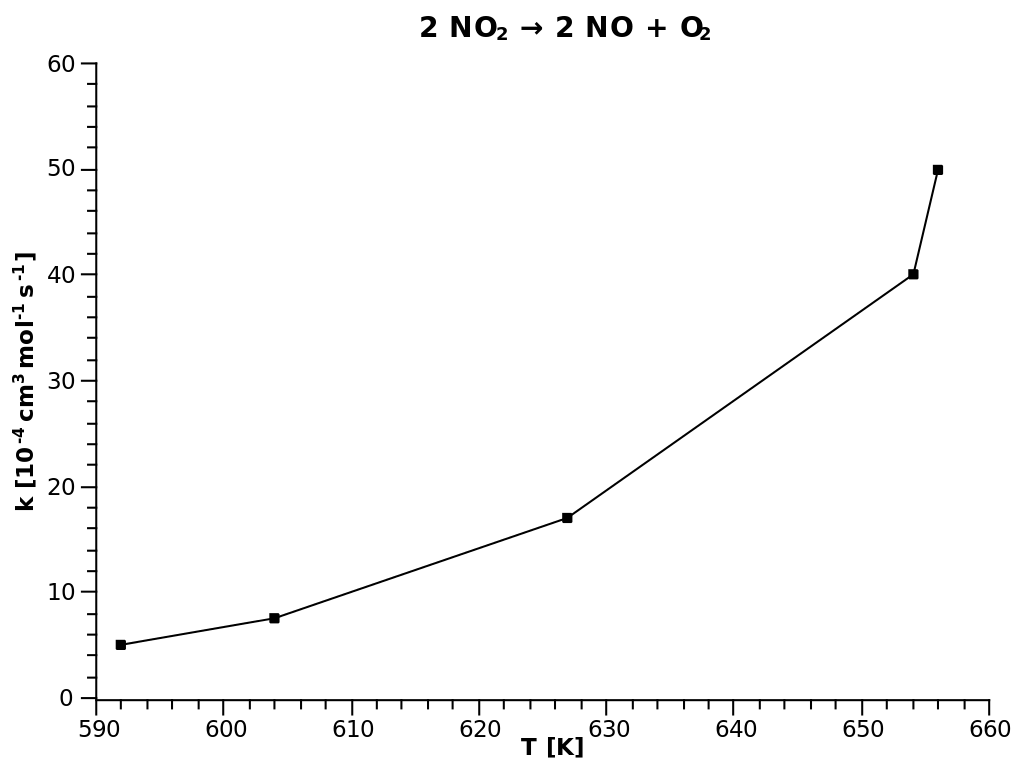
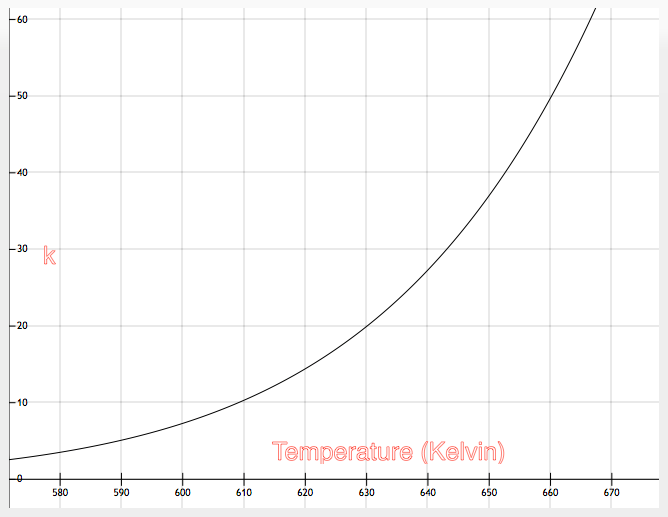
Анализируя выражение (5.3), приходим к выводу, что существуют две принципиальные возможности ускорения реакции: Предэкспоненциальный множитель в уравнении аррениуса таблицаДанное построение используется в химической кинетике и выполняется в координатах логарифма константы скорости реакции ($ln(k)$, ось ординат) от обратной температуры ($1/T$, ось абсцисс). Чаще всего используются для анализа влияния температуры на скорость химической реакции. Для реакции первого порядка данное построение имеет вид прямой линии, из которой можно определить энергию активации и предэкспоненциальный множитель. Наша рабочая группа в статьях и тезисах приводит полное построение и сопутствующее ему описание, если позволяет объём публикации. При сильно сжатом объёме приводится только уравнение для построения линии и полученные результаты. СложноУравнение Аррениуса может быть записано в форме ур. 1 или ур. 2: Различие между способами записи в единицах измерения энергии. Ур. 1 использует соотношение энергия/моль, типичное для химии, ур. 2 использует непосредственно энергию, что более типично для физики. Учитываются различные единицы при использовании либо газовой постоянной $R$, либо постоянной Больцмана $k_B$. Ур. 2 может быть расширено до ур. 3: где $k$ — константа скорости, $A$ — предэкспоненциальный множитель, $E_a$ — энергия активации, $R$ — универсальная газовая постоянная, $T$ — абсолютная температура, К. При построении, описанном в разделе “Просто”, значение пересечения графика с осью OY даёт $ln(A)$, а угловой коэффициент прямой будет равен $-E_a/R$. Эти значения могут быть получены путём простой линейной регрессии при помощи электронной таблицы (пример). Предэкспоненциальный множитель $A$ является эмпирической константой пропорциональности, которая была оценена различными теориями, учитывающими такие факторы, как частота столкновения между реагирующими частицами, их относительная ориентация и энтропия активации. Выражение $e^<-E_a/RT>$ представляет долю молекул в газе, имеющих энергии, равные или превышающие энергию активации при определенной температуре. Практически во всех случаях $E_a \gg RT$, так что это отношение очень мало и быстро растёт с увеличением $T$. В результате константа скорости реакции $k$ быстро увеличивается с температурой $T$, как показано на прямой линии графика $k(T)$. Чисто математически при очень высоких температурах возможна ситуация, в который $E_a \ll RT$, тогда $k$ должна выровняться и приблизиться к $A$, как к пределу. На практике никогда такого не было.
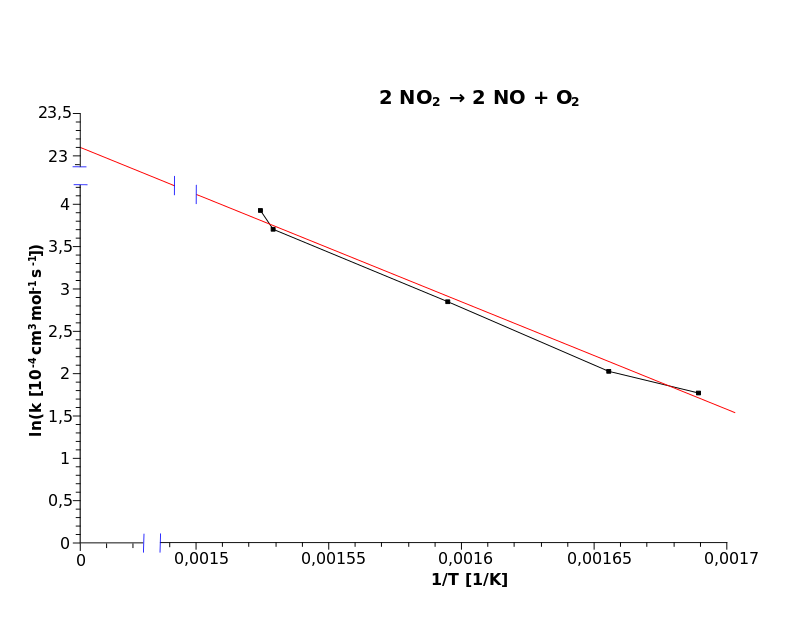
ПримерОбратимся к красной “линии наилучшего соответствия” на рис. 2. Возьмём с графика следующие точки: Угловой коэффициент красной линии будет равен $(4,1 — 2,2) / (0,0015 — 0,00165) = -12,667$ Точка пересечения (значение $y$ при $x = 0$) для красной линии будет равна $4,1 + (0,0015 * 12667) = 23,1$ Подставив данные значения в ур. 3, получим: Можно выполнить построение:
Отсюда $k = 1,08 * 10^ <10>* e^<-12,667/T>$ для $k$ в $10^ <-4>* см^3 * моль^ <-1>* с^<-1>$ и $T$ в К. Выполним подстановку в отношение $-E_a / R = -12,667 K$ которое при приблизительном значении $R = 8,31446$ $Дж * K^ <−1>* моль^<−1>$ даст нам энергию активации, полученную из наших данных: $E_a = R * 12,667 K = 105300$ $Дж * моль^ <−1>= 105,3$ $кДж * моль^<−1>$. Мне кажется, что это довольно просто. Попробуйте и вы! Предэкспоненциальный множитель в уравнении аррениуса таблицаФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ Конспект лекций для студентов биофака ЮФУ (РГУ) 2.1 СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ 2.1.9 Влияние температуры на константу скорости реакции Константа скорости реакции есть функция от температуры; повышение температуры, как правило, увеличивает константу скорости. Первая попытка учесть влияние температуры была сделана Я. Г. Вант-Гоффом, который сформулировал следующее эмпирическое правило: При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза. Величина, показывающая, во сколько раз увеличивается константа скорости при повышении температуры на 10 градусов, есть температурный коэффициент константы скорости реакции γ . Математически правило Вант-Гоффа можно записать следующим образом: Однако правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры). 2.1.10 Уравнение Аррениуса Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. С. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации. Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию. Рассмотрим путь некоторой элементарной реакции Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом: Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер. Энергия активации реакции приближённо равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е’А выше, нежели энергия активации прямой реакции EA. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции. Вышесказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 2.5). Рис. 2.5 Энергетическая диаграмма химической реакции. Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6): Рис. 2.6 Распределение частиц по энергии Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом: Представив изменение энтальпии реакции ΔHº в виде разности двух величин E1 и E2, получаем: Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где EA – энергия активации : После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме: Рис. 2.7 Зависимость логарифма константы скорости химической Здесь A – постоянная интегрирования. Из уравнения (II.37) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (II.36), логарифм константы скорости линейно зависит от обратной температуры (рис.2.7); величину энергии активации EA и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат). Зная энергию активации реакции и константу скорости при какой-либо температуре T1, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T2: источники: http://count0.ru/students/kinetics/arrh/ http://physchem.chimfak.sfedu.ru/Source/PCC/Kinetics_4.htm |




 ),
),  – доля активных, т. е. благоприятных в энергетическом отношении соударений.
– доля активных, т. е. благоприятных в энергетическом отношении соударений.
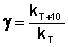 (II.29)
(II.29)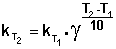 (II.30)
(II.30)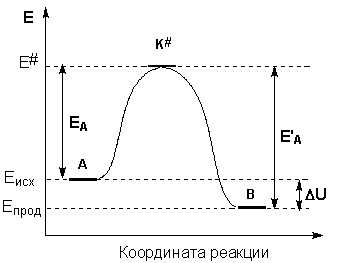
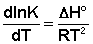 (II.31)
(II.31)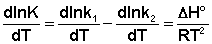 (II.32)
(II.32)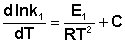 (II.33)
(II.33)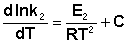 (II.34)
(II.34)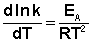 (II.35)
(II.35)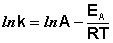 (II.36)
(II.36)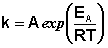 (II.37)
(II.37)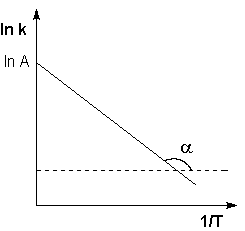
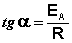 (II.38)
(II.38)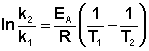 (II.39)
(II.39)