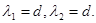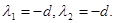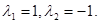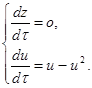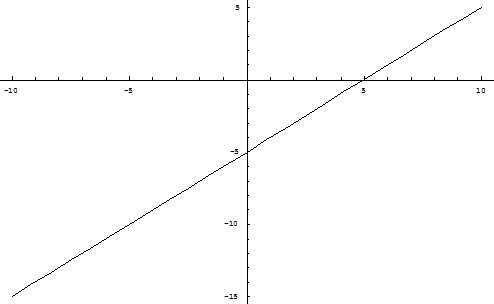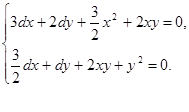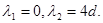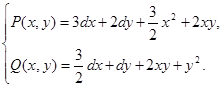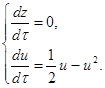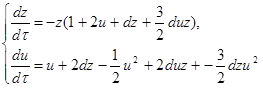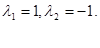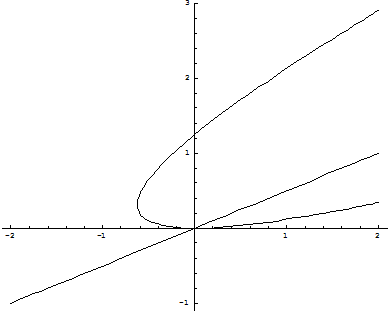Метод изоклин для дифференциальных уравнений 1-го порядка
Дифференциальное уравнение первого порядка
Если в каждой точке области задано значение некоторой величины, то говорят, что в области задано поле этой величины. Таким образом, дифференциальное уравнение (1) определяет поле направлений.
Тройка чисел определяет направление прямой, проходящей через точку . Совокупность отрезков этих прямых дает геометрическую картину поля направлений.
Задача интегрирования дифференциального уравнения (1) может быть теперь истолкована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке.
Задача построения интегральной кривой часто решается введением изоклин . Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и тоже направление. Семейство изоклин дифференциального уравнения (1) определяется уравнением
где — параметр. Придавая параметру близкие числовые значения, получаем достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального yравнения (1).
Замечание 1. Нулевая изоклина дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых.
Для большей точности построения интегральных кривых находят также геометрическое место точек перегиба. Для этого находят в силу уравнения (1):
и приравнивают ее нулю. Линия, определяемая уравнением
и есть возможное геометрическое место точек перегиба.
Пример 1. С помощью изоклин построить приближенно интегральные кривые дифференциального уравнения .
Решение. Для получения уравнения изоклин положим , тогда или .
Изоклинами являются параллельные прямые. При получим изоклину . Эта прямая делит плоскость на две части, в каждой из которых производная имеет один и тот же знак (рис. 6).
Интегральные кривые, пересекая прямую , переходят из области убывания функции в область возрастания, и наоборот, а значит на этой прямой находятся точки экстремума интегральных кривых, именно точки минимума.
Возьмем еще две изоклины: и .
Касательные, проведенные к интегральным кривым в точках пересечения с изоклинами и , образуют с осью углы в и соответственно. Найдем далее вторую производную .
Прямая , на которой , является изоклиной, получаемой при , и в то же время интегральной линией, в чем можно убедиться подстановкой в уравнение. Так как правая часть данного уравнения удовлетворяет условиям теоремы существования и единственности во всей плоскости , то остальные интегральные кривые не пересекают эту изоклину. Изоклина , на которой находятся точки минимума интегральных кривых, расположена над изоклиной , а поэтому интегральные кривые, проходящие ниже изоклины , не имеют точек экстремума.
Прямая делит плоскость на две части, в одной из которых (расположенной над прямой) 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFEIdthoX7wMRGRsJ7q5I0AAAEISURBVCjPY2CgDLDM4HqMU5LtGccrnJLsE5gC0IQYrQSgLNYDfAlokitrgqEsPwfLDWiumMZg6QBhJjG0g2l3B5gkzwMGuQMQ5jEGLTDNrG4As0iRQSiQgfuSAYPZBgaoFq4iQwhDDij5kEFoTSBDEJJdRYlgeh9Q8jVDBmsAywtkl5SCZe0UGJgeM5isa2BDCR3uVpC968CSDH0O7A8xJeXAxjKoCrAqIBvbmsgIpCSBkhMZGN8y+DUgWwkJKnagPwsYGIMY6gyQHAv1CjCW7AwYGC1r58GCmIFZCa4utWMakNxoPReuERF8DCzJQDZnIBv2eBYERciBlQk445lH6TKe9COIWwoABhM22oebiGoAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, а значит интегральные кривые обращены вогнутостью вверх, а в другой и, значит, интегральные кривые обращены вогнутостью вниз. Интегральные кривые не пересекают прямой , значит, она не является геометрическим местом точек перегиба. Интегральные кривые данного уравнения не имеют точек перегиба.
Проведенное исследование позволяет нам приближенно построить семейство интегральных кривых уравнения (рис.6).
Пример 2. Методом изоклин построить приближенно интегральные кривые дифференциального уравнения .
Решение. Полагая , где , получаем уравнение изоклин , причем . При получим , откуда
Интегральные кривые в точках пересечения с этими изоклинами имеют горизонтальные касательные.
Определим, имеют ли интегральные кривые на изоклинах экстремум. Для этого найдем вторую производную:
Если четное, то 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFEIdthoX7wMRGRsJ7q5I0AAAEISURBVCjPY2CgDLDM4HqMU5LtGccrnJLsE5gC0IQYrQSgLNYDfAlokitrgqEsPwfLDWiumMZg6QBhJjG0g2l3B5gkzwMGuQMQ5jEGLTDNrG4As0iRQSiQgfuSAYPZBgaoFq4iQwhDDij5kEFoTSBDEJJdRYlgeh9Q8jVDBmsAywtkl5SCZe0UGJgeM5isa2BDCR3uVpC968CSDH0O7A8xJeXAxjKoCrAqIBvbmsgIpCSBkhMZGN8y+DUgWwkJKnagPwsYGIMY6gyQHAv1CjCW7AwYGC1r58GCmIFZCa4utWMakNxoPReuERF8DCzJQDZnIBv2eBYERciBlQk445lH6TKe9COIWwoABhM22oebiGoAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, и, значит, в точках пересечения с изоклинами , интегральные кривые имеют минимум; если же нечетное, то и интегральные кривые в точках пересечения с изоклинами имеют максимум. Находим изоклины:
Изоклинами являются параллельные прямыми с угловым коэффициентом, равным –1 , т. е. изоклины пересекают ось под углом . Легко убедиться в том, что изоклины , являются интегральными кривыми данного дифференциального уравнения (для этого достаточно подставить функции в уравнение ).
Во всех точках плоскости правая часть данного уравнения, т.е. функция , удовлетворяет всем условиям теоремы существования и единственности, а поэтому интегральные кривые не пересекаются, и, следовательно, не пересекают изоклины . Производная обращается в ноль при , т.е. на изоклинах (6), и при , т. е. на изоклинах (6) и (7). При переходе (слева направо) через изоклины (7) меняет знак с плюса на минус. Например, если рассмотреть полосу, заключенную между изоклинами и , то на изоклине производная , причем под изоклиной 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFEIdthoX7wMRGRsJ7q5I0AAAEISURBVCjPY2CgDLDM4HqMU5LtGccrnJLsE5gC0IQYrQSgLNYDfAlokitrgqEsPwfLDWiumMZg6QBhJjG0g2l3B5gkzwMGuQMQ5jEGLTDNrG4As0iRQSiQgfuSAYPZBgaoFq4iQwhDDij5kEFoTSBDEJJdRYlgeh9Q8jVDBmsAywtkl5SCZe0UGJgeM5isa2BDCR3uVpC968CSDH0O7A8xJeXAxjKoCrAqIBvbmsgIpCSBkhMZGN8y+DUgWwkJKnagPwsYGIMY6gyQHAv1CjCW7AwYGC1r58GCmIFZCa4utWMakNxoPReuERF8DCzJQDZnIBv2eBYERciBlQk445lH6TKe9COIWwoABhM22oebiGoAAAAASUVORK5CYII=» style=»vertical-align: middle;» />. Значит, интегральные кривые обращены вогнутостью вверх, а над изоклиной , значит, интегральные кривые обращены вогнутостью вниз. Таким образом, изоклины (7) являются геометрическим местом точек перегиба интегральных кривых. Полученные данные позволяют приближенно построить семейство интегральных кривых данного уравнения. Для более точного построения следует нанести еще несколько изоклин (рис. 7).
Пример 3. Методом изоклин построить интегральные кривые уравнения .
Решение. Положим . Тогда уравнение изоклин будет
Изоклинами являются параболы с вертикальной осью симметрии . Среди изоклин нет интегральных кривых. В самом деле, подставляя в данное уравнение и , будем иметь , или . Но это равенство ни при каком значении не может выполняться тождественно относительно .
Пусть , тогда в точках пересечения с изоклиной интегральные кривые будут иметь горизонтальные касательные. Изоклина разбивает плоскость на две части: в одной из них (решения убывают), а в другой 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADQAAAAXBAMAAAC2bnFAAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAncEhYUEQgTHg8NGxUXFruPrBAAAA30lEQVQoz2NgIB8wr8MpxfIFpxTjAnSRDhiDUwBNplNwBpRlb4Bh9y2okBOYTIQrYPzAwAU1SARMsp4JgEpxb2BgmsDAJtTAcDcBao4QVI5fgYHpAwNT4wSGOXA7pB3gUt8Y3LknMH9H2F8NlusHSn1lCO5/wPIV4TY2sBw/WIqh3oDnA7JUAdxABm0GLgU0TQycQBcCA+gjg30BujOA/uIH+msOgzzMO3DHM39hiAcyvYTWQ2VYD8HUMHiKTwGantCwEMpPbEDYCQoFrgl8n3FElX1BlwMOKXadE6QnGABHNTFBqOdYeAAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> (решения возрастают). И так как эта изоклина не является интегральной кривой, то на ней находятся точки экстремума интегральных кривых, именно на той части параболы , где — точки минимума, а на другой части этой параболы, где 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcChQSFZMdCB6RCQsVNol/AAAACdSURBVBjTY2AgCbDjEBexE8Aqzrl2HbJEZQCcKaiHLMGiDJdhBEvs0dymDJVxQJbgVpForkqAyBg5IEnwOPC+ngeRYGA1SkRIsDFIKWyHGc5qlQCXYGSImwB3AOsJhAQDY54DXBzZKGaDewISEGezGzkIIiTqtFcxZEIcpQvTKtAHVMBxwsPoAKoHWd69ewe0t5AhEMwtRgoSQUEGAFJBHb3FaZBuAAAAAElFTkSuQmCC» /> — точки максимума. Интегральная кривая, проходящая через точку , т.е. через вершину параболы , в этой точке не имеет экстремума. В точках изоклин и касательные к интегральным кривым имеют угловые коэффициенты, соответственно равные 1 и –1.
Для исследования направления вогнутости интегральных кривых найдем вторую производную:
Она обращается в ноль только в точках, лежащих на параболе . В точках плоскости , координаты которых удовлетворяют условию , интегральные кривые вогнуты вниз , а в точках, где x^2″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADkAAAAYCAMAAAB3NqUkAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEXRSTlMA0KEwwGKBBhD6IUGwkHFR4HWSoZwAAAD0SURBVDjLvVTZrsQgCBVBAnVp//9rB6fJ1FJz78SH4alBD/YsGsLvSpjzGrBsu/IKMukWmq4gsUjYFRepRlgE4uqRQtt8gdM/wCghydwv+AsrUJlPnlJp7z/fRiz7oTsVxFjQPqziu1eQuz10jIOTw1Y2E0GIhl6uoXSkRuc4xEsItMWsKWsZkZvo2X+kBaJ8NplyFp4sLk/Gs+pD6kxx3Hijc1bRWT8d8T7L0+kgevadQonsghiddqdE5k4baQofzhXSrWgOSD6GkY6LZk+Cd7MBpQaVHnnNAhfNOkuQ2CzxGoJOPfmizF2c6PbN80AEOfyyXgEyBo3d+df6AAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, они вогнуты вверх 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFEIdthoX7wMRGRsJ7q5I0AAAEISURBVCjPY2CgDLDM4HqMU5LtGccrnJLsE5gC0IQYrQSgLNYDfAlokitrgqEsPwfLDWiumMZg6QBhJjG0g2l3B5gkzwMGuQMQ5jEGLTDNrG4As0iRQSiQgfuSAYPZBgaoFq4iQwhDDij5kEFoTSBDEJJdRYlgeh9Q8jVDBmsAywtkl5SCZe0UGJgeM5isa2BDCR3uVpC968CSDH0O7A8xJeXAxjKoCrAqIBvbmsgIpCSBkhMZGN8y+DUgWwkJKnagPwsYGIMY6gyQHAv1CjCW7AwYGC1r58GCmIFZCa4utWMakNxoPReuERF8DCzJQDZnIBv2eBYERciBlQk445lH6TKe9COIWwoABhM22oebiGoAAAAASUVORK5CYII=» style=»vertical-align: middle;» />. Точки пересечения интегральных кривых с параболой являются точками перегиба этих кривых. Итак, парабола есть геометрическое место точек перегиба интегральных кривых.
Правая часть исходного уравнения во всех точках плоскости удовлетворяет условиям теоремы существования и единственности, поэтому через каждую точку плоскости проходит единственная интегральная кривая уравнения.
Используя полученные сведения, строим приближенно семейство интегральных кривых данного уравнения (рис. 8).
Замечание 2. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.
Рассмотрим уравнение . Семейство изоклин определяется уравнением . Это семейство прямых, проходящих через начало координат, так что в начале координат пересекаются изоклины, отвечающие различным наклонам касательных к интегральным кривым. Нетрудно убедиться, что общее решение данного уравнения имеет вид и точка является особой точкой дифференциального уравнения. Здесь изоклины являются интегральными кривыми уравнения (рис. 9).
Пример 4. Методом изоклин построить интегральные кривые уравнения .
Решение. Полагая , получаем уравнение семейства изоклин . Таким образом, изоклинами являются прямые, проходящие через начало координат .
При получим изоклину , при — изоклину , при — изоклину .
Рассматривая обратное уравнение найдем изоклину , во всех точках которой интегральные кривые имеют вертикальные касательные.
В точке пересекаются все изоклины данного уравнения (особая точка уравнения). С помощью полученных изоклин строим интегральные кривые (рис. 10).
Исследование качественного поведения математических моделей синергетических систем (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
Практикум по курсу «Прикладная синергетика»
Исследование качественного поведения математических моделей синергетических систем
1. Исследование качественного поведения математических моделей синергетических систем
(Методические указания по выполнению практических заданий)
1.1 Общие положения.
Данные практические задания выполняются в соответствии с учебным планом по дисциплине «Общая синергетика». Выполнению работ должно предшествовать изучение теоретического материала (лекции и литературные источники). Описание лабораторных работ также содержит некоторые основные теоретические положения качественной теории обыкновенных дифференциальных уравнений и содержит ряд контрольных вопросов (заданий). Задание может считаться успешно выполненным, если не только получены правильные ответы на контрольные вопросы, но и приведены обоснования этих ответов со ссылками на соответствующие теоретические положения. Кроме того, в практических заданиях предусмотрено самостоятельное решение задач по теме выполняемой работы.
По результатам работы необходимо представить отчет, который должен содержать:
- Название практического задания и номер упражнения, номер задачи или контрольного вопроса; цель работы решения задач и ответы на контрольные вопросы с теоретическим обоснованием; необходимые графические иллюстрации; дополнительные сведения и соображения по теме практического задания (по желанию студента).
2. Практические задания
Элементы качественной теории обыкновенных дифференциальных уравнений (теоретические сведения к заданиям 1 – 3)
Во всех системах, представляющих интерес для синергетики, решающую роль играет динамика. А. Пуанкаре разработал современную теорию динамических систем, цель которой — исследовать типы поведения систем, описываемых взаимосвязан-ными нелинейными уравнениями. Эволюцию этих систем во времени можно описать, с помощью представления о движении изображающей точки в фазовом пространстве. Поскольку имеется взаимно однозначное соответствие между движением динамических систем и движением в фазовом пространстве (характером фазовых траекторий), то изучая возможные типы последних, можно придти к качественной классификации явлений, наблюдаемых в динамических системах. В данной лабораторной работе рассматриваются динамические системы с конечным числом переменных, исключая пространственно распределенные системы, характеризуемые непрерывной зависимостью от пространственных координат.
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ. Динамические уравнения для систем с конечным числом степеней свободы имеют вид dq/dt = F( q, л) , где q – n — мерный вектор, а л – некоторый (управляющий) параметр. Решение q(t) уравнения dq/dt = F(t, q) представляется геометрически графиком функции q(t). Этот график определяет интегральную кривую на плоскости t, q.
Если F непрерывна в D (обл. существования решений), то интегральные кривые заполняют область D плоскости t, q. Это следует из того, что каждая точка D должна лежать по крайней мере на одной интегральной кривой. Таким образом, решения дифференциального уравнения представляются семейством интегральных кривых в D.
Если обе функции F и дF/дq непрерывны в D, то существует единственная интегральная кривая, проходящая через каждую точку D (см.). Заметим, что семейства интегральных кривых на рис. 2 и 6 имеют между собой большое сходство. Любая интегральная кривая на одном рисунке имеет соответствующую ей кривую на другом; они похожи по форме, у них те же самые асимптоты, но они не идентичны. Соотношение между этими двумя семействами интегральных кривых является примером того, что мы будем называть качественной эквивалентностью. Мы будем говорить, что качественное поведение интегральных кривых на рис. 2 такое же, как на рис. 6.
Рис.1-6. Примеры интегральных кривых
Сказанное выше приводит к двум важным идеям:
1. Два различных дифференциальных уравнения могут иметь решения с одинаковым качественным поведением.
2. Качественное поведение решений определяется функцией F (t, q).
АВТОНОМНЫЕ УРАВНЕНИЯ. ИНТЕГРАЛЬНЫЕ КРИВЫЕ И ФАЗОВЫЙ ПОРТРЕТ
Дифференциальное уравнение вида dq/dt=F(q), называется автономным. Это название оправдано тем, что F(q), определяется одним только q, и, таким образом, решение само управляет своим изменением.
Для семейств интегральных кривых, в которых кривые получаются одна из другой сдвигами, качественное поведение семейства определяется качественным поведением каждого индивидуального решения, а оно в свою очередь определяется функцией F(q). Если F(q) 
Эти свойства решений удобнее изображать на оси q, чем на плоскости t, q. Если F(q) 
*) Употребляются и другие эквивалентные термины: «стационарная точка», «особая точка», «положение равновесия». Ось q называется при этом фазовой прямой, а точка q(t))—фазовой точкой.
Несколько фазовых портретов для конкретных функций F изображено на рис. 7 — 10.
Если решение q(t) нестационарное, то оно должно быть либо возрастающим, либо убывающим; таким образом, если число неподвижных точек конечно, то может существовать только конечное число «различных» фазовых портретов. Под словом «различные» мы подразумеваем «отличающиеся набором областей, в которых возрастает или убывает». Например, рассмотрим случай одной неподвижной точки q = с (см. рис. 11). На каждой из получаемых полупрямых
(q с) функция F может быть либо положительной, либо отрицательной. Следовательно фазовый портрет должен соответствовать одному из четырех случаев, изображенных на рис. 11.
Рис. 11. Четыре возможных фазовых портрета для одной изолированной неподвижной точки. Неподвижная точка называется аттрактором в случае (а), шунтом в случаях (b) и (с) и репеллером в случае (а).
Это значит, что качественное поведение любого автономного дифференциального уравнения с одной неподвижной точкой должно соответствовать одному из фазовых портретов на рис. 11 при некотором значении с.
Различные дифференциальные уравнения с одной неподвижной точкой, имеющие один и тот же фазовый портрет, считаются качественно эквивалентными.
Заметим, что соображения, которые использовались при получении рис. 11, сохраняют свою силу, если точка q = с — одна из многих неподвижных точек на фазовом портрете. Другими словами, качественное поведение q в окрестности любой неподвижной точки должно быть таким же, как в одном из случаев на рис. 11. Говорят, что это поведение определяет характер (вид, природу) неподвижной точки, и для его описания применяют термины, приведенные в подписи к рис. 11.
Таким образом, из сказанного следует вывод, что фазовый портрет любого автономного уравнения полностью определяется видом его неподвижных точек. Введем следующее определение.
Определение. Два дифференциальных уравнения вида dq/dt = F(q) качественно эквивалентны, если они имеют равное количество неподвижных точек одинакового характера, расположенных в одинаковом порядке на фазовой прямой.
Например, уравнение dq/dt = (q + 2) (q + 1) эквивалентно уравнению dq/dt = 1/2 (q2 — 1). Оба уравнения имеют по две неподвижные точки, одна из которых аттрактор, а другая репеллер, причем аттрактору соответствует меньшее значение q. Уравнение dq/dt = — (q + 2) (q + 1) не является качественно эквивалентным уравнению dq/dt =1/2 (q2 — 1), потому что аттрактор и репеллер идут в обратном порядке.
Для нелинейных функций F(q) каждая неподвижная точка должна принадлежать одному из возможных типов, указанных на рис. 11. Таким образом, хотя и может существовать бесконечно много различных фазовых портретов, они содержат не более четырех различных видов неподвижных точек. Это ограничение связано с тем, что уравнение dq/dt = F(q) содержит только одну действительную переменную q. Поэтому возникает одномерный фазовый портрет, на котором q в каждой нестационарной точке может только возрастать или убывать.
Упражнение 1. Каким из нижеприведенных уравнений соответствуют семейства интегральных кривых, изображенные на рис. рис. 1 – 6.
dq/dt =2qt (4) dq/dt = — q/t, t 

Упражнение 2. Распределить следующие дифференциальные уравнения на группы качественно эквивалентных:
Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго и первого порядков
| Название: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго и первого порядков Раздел: Рефераты по математике Тип: дипломная работа Добавлен 10:02:27 04 сентября 2009 Похожие работы Просмотров: 40 Комментариев: 21 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||
 |

Приравнивая коэффициенты при одинаковых степенях x m y n слева и справа, получим равенства:
Предполагаем, что кривая не проходит через начало координат, тогда p ≠0 , значит Р=0 .
Из равенств (1.13) получаем, что М=а1, N=1,
n = 
p = ( 
Подставим эти коэффициенты в уравнение (1.14) и получим ещё одно условие на коэффициенты системы, которое совпадает с условием (1.8), то есть:
Итак, имеет место следующая теорема:
Имеет частный интеграл mx+ny+p=0, коэффициенты которого выражаются формулами
n = 

При условии, что коэффициенты системы связаны соотношением:
1.3 Необходимые и достаточные условия существования у двумерной стационарной системы двух частных интегралов в виде кривых первого и второго порядков
В подразделах 1.1–1.2 мы получили что система (1.1) будет иметь два частных интеграла в виде кривой первого порядка и кривой второго порядка, при условии, что коэффициенты системы связаны соотношениями:
Из этих равенств получили:
а = —
Так как коэффициент d можно взять любым, неравным нулю, тогда предположим, что b =2 d . Из следующих предположений, получаем:
a = —
Получили, что коэффициенты системы (1.1) определяются формулами (1.17), при условиях (1.16), в которых параметры b 1 = b 2 =с2 =1, а1 ≠0.
Выражения (1.6), (1.9), (1.15) при условии, что имеют место (1.17), дадут следующие выражения для коэффициентов интегралов (1.3) и (1.11):
n =
p =
Имеет место следующая теорема:

Имеет частные интегралы вида:
При условии, что коэффициенты системы (1.1) выражаются через параметры а1 и d по формулам (1.17) и в1 =в2 =с2 =1.
2. Рассмотрим случай:
Выразим из этого условия коэффициент с , получим
Воспользуемся предположением из первого случая, что в=2 d , d ≠0, тогда коэффициент с=а1 (2а1 –3) d – (а1 –2) а.
Так как d -любое число, неравное нулю, предположим, что а=2а1 d .
Равенства (1.6) – (1.9) и (1.14) при условии, что имеют место формулы (1.19), дадут следующие выражения для коэффициентов интегралов (1.3) и (1.11):
δ=2 (a1 –
σ=(a1 – 
n =
p =m 


Имеет частные интегралы вида:
y 2 +2 (a1 –2) xy+(a1 –2) 2 x 2 +2 (a1 –1) dy+2 (a1 –

При условиях, что коэффициенты системы (1.1) выражаются через параметры а1 и d по формулам (1.19) и в1 =в2 =с2 =1, а1 ≠2, а1 ≠0, d-любое число.
2 Качественное исследование построенных классов систем
2.1 Исследование одной системы из первого класса построенных двумерных стационарных систем
Будем проводить исследование системы в предположении, что коэффициенты её определяются согласно формулам (1.17):
a= —
Тогда система (1.1) запишется в виде:


Интегральные кривые в этом случаи имеют вид:
y 2 –2xy+x 2 –2dy+2dx+d 2 =0, (2.2)
При рассмотрении этого случая заметим, что интегральная кривая второго порядка y 2 –2 xy + x 2 –2 dy +2 dx + d 2 =0 представляет собой две совпадающие прямые вида x – y + d =0 , то есть:
Значит, если а1 =в1 =в2 =с2 =1 и если выполняются условия (1.17) система (1.1) имеет только один частный интеграл вида:
Найдём состояния равновесия системы (2.1). Приравняв правые части системы к нулю и, решив полученную систему, найдём точки покоя системы.
Система имеет четыре состояния равновесия:
О (0,0), А (-d, 0), B(-d, d), C(-
Исследуем поведение траекторий в окрестностях состояний равновесия.
1. Исследуем точку О (0,0).
Составим характеристическое уравнение для точки имеет вид О (0,0):


Характеристическими числами для точки О (0,0) системы (2.1) будут
Корни характеристического уравнения действительные, одного знака, но в зависимости от параметра d точка О (0,0) – устойчивый узел, если d 0.
Из Главы 1. случай d =0 не рассматривается.
2. Исследуем точку А (-d, 0).
Составим характеристическое уравнение в точке А (-d, 0).
Следовательно, характеристическое уравнение примет вид:


Характеристические числа для точки А (-d, 0) системы (2.1) будут
Корни λ1 ,λ2 – действительные, одного знака. В зависимости от параметра d.
Точка А (-d, 0) является неустойчивым узлом, если d 0.
3. Исследуем точкуВ (-d, d).
Составим характеристическое уравнение в точке В (-d, d).
Согласно равенствам (2.4) характеристическое уравнение примет вид:


λ1 ,λ2 – характеристические числа для точки В (- d , d ) системы (2.4).
Корни λ1 ,λ2 –действительные, одного знака зависящие от параметра d.
Если d 0, то точка В (- d , d ) – неустойчивый узел.
4. Исследуем точку С(-
Составим характеристическое уравнение в точке С(-


Характеристические числа для точки С(-

Корни λ1 ,λ2 –действительные, различных знаков, независимо от параметра d.
Значит, точка С(—
Исследуем бесконечно-удалённую часть плоскости на концах оси ОY. Преобразование x=


Для исследования состояний равновесий на концах оси ОУ, нам необходимо исследовать только точку No (0,0).Составим характеристическое уравнение в точке No(0,0):

Корни λ1 ,λ2 –действительные и различных знаков не зависимо от параметра d. Значит, точка No (0,0) – седло.
Исследуем бесконечно-удалённую часть плоскости вне концов оси ОУ преобразованием [1] 

Изучим бесконечно-удалённые точки на оси U, то есть при z=0, получаем:
Таким образом, получаем две точки N1 (0,0), N2 (0,1), которые являются состоянием равновесия. Исследуем характер этих точек обычным способом.
1. Исследуем точку N1 (0,0).
Составляем характеристическое уравнение в точке N1 (0,0):

Корни λ1 , λ2 –действительные и различных знаков. Следовательно, точка N1 (0,0) – седло.
2. Исследуем точку N2 (0,1).
Составим характеристическое уравнение в точке N2 (0,1):

Корни λ1 ,λ2 –действительные и одного знака (–). Следовательно, точка N2 (0,1) – устойчивый узел.
Дадим распределение состояний равновесия системы (2.1) в виде таблицы 1.
| d | O (0,0) | A (-d, 0) | B (-d, d) | C( ) ) | ∞ | ||
| N0 | N1 | N2 | |||||
(-∞; 0) | Уст.у. | Неуст.у. | Уст.у | Седло | Седло | Уст.у. | Седло |
| (0;∞) | Неуст.у. | Уст.у. | Неуст.у. | Седло | Седло | Уст.у. | Седло |
Положение кривой (2.3) и расположение относительно их состояний равновесия при d 0 представлено на рис. 1 (а, б).
Поведение траекторий системы (2.1) в целом при d 0 представлено на рис. 3 (а, б) приложения А.
Исследуя вид кривых (2.2) и расположение относительно их состояний равновесия, убеждаемся, что система (2.1) не имеет предельных циклов, так как Воробьёв А.П. [10] доказал, что для систем, правые части которых есть полиномы второй степени, предельный цикл может окружать только точку типа фокуса. Учитывая расположение состояний равновесия относительно кривых (2.2), являющиеся интегралами системы (2.1) не может существовать предельных циклов, окружающих несколько состояний равновесия.
2.2 Исследование одной системы из второго класса построенных двумерных стационарных систем
Рассмотрим систему (1.1) в предположении, что в1 =в2 =с2 =1, а1 =
и коэффициенты определяются формулами (1.19). Тогда система (1.1) будет иметь вид:

Интегральные кривые в этом случае имеют вид:
— 
Найдём состояния равновесия системы (2.7). Для этого приравняем правые части системы нулю:
Решая эту систему, получим две пары точек, которые являются точками покоя системы (2.7): О (0,0), А(
Исследуем поведение траекторий решений системы (2.7) в окрестностях состояний равновесия О (0,0), А(
1 . Исследуем точку О (0,0).
Составим характеристическое уравнение системы в точке О (0,0):


Характеристическими числами для точки О (0,0), будут
Так как один корень нулевой, тогда точка О (0,0) является сложным состоянием равновесия (изолированное состояние равновесия), для которого требуется дополнительное исследование. Для определения характера состояния равновесия О (0,0) воспользуемся теоремой [5].
Теорема 2.1 Пусть точка (0,0) – изолированное состояние равновесия системы:
1) при m -нечётном и ∆ m >0 точка (0,0) – есть топологический узел;
c 1 x 1 + c 2 x 1 2 + … + 

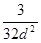
x 1 1 : 
x 1 2 : с2 +


Следовательно с1 =0, с2 =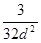
Тогда y1 =φ(x1 )= 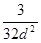
Находим ψ(х1 )=Р2 (х1 ,φ(х1 ))=


Получили m=3-нечётное, ∆m >0.
Следовательно, по теореме 2.1 получаем, что точка О (0,0) – топологический узел.
2 . Исследуем точку А(
Составим характеристическое уравнение в точке А(
Qx (x, y)=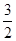
Следовательно, характеристическое уравнение имеет вид:

Характеристическими числами для точки А(

Корни λ1 , λ2 –действительные и одного знака, зависящие от параметра d. Если d 0, тогда точка А(
Исследуем бесконечно-удалённую часть плоскости системы (2.7) вне концов оси ОУ. Преобразование [1] 

Изучим бесконечно-удалённые точки на оси U, то есть z=0. Получаем:
Следовательно, 

Таким образом, получили две точки N1 (0,0), N2 (0,
1. Исследуем точку N1 (0,0).
Составим характеристическое уравнение в точке N1 (0,0):

λ1 = 

Корни λ1 ,λ2 –действительные и различных знаков, следовательно, точка N1 (0,0) – седло.
2. Исследуем точку N2 (0,
Составим характеристическое уравнение в точке N2 (0,
Pz = 
Qz = 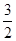
Qu = 
Характеристическое уравнение имеет вид:

Следовательно, характеристические числа:
λ1 =

Корни λ1 ,λ2 –действительные, различных знаков, значит точка N2 (0,
Исследуем бесконечно-удалённые концы оси ОУ с помощью преобразования [1] x=

Для исследования состояний равновесия на концах оси ОУ, нам необходимо исследовать только точку (0,0), которая является состоянием равновесия данной системы. Составим характеристическое уравнение в точке (0,0):

Корни λ1 ,λ2 –действительные и различных знаков, значит точка (0,0) – седло.
Теперь дадим распределение состояний равновесия системы (2.7) в виде таблицы 2.
| d | O (0,0) | A(  ) ) | ∞ | ||
| N0 | N1 | N2 | |||
| (-∞; 0) | Седло | ||||
Положение кривых (2.8), (2.9) и расположение относительно их состояний равновесия при d 0 даётся соответственно рис. 2 (а, б).
Поведение траекторий системы (2.7) в целом при d 0 представлено на рис. 4 (а, б) приложения Б.
Так как Воробьёв А.П. [10] доказал, что для систем, правые части которых есть полиномы второй степени, предельный цикл может окружать только точку типа фокуса, тогда исследуя вид кривых (2.8), (2.9) и расположение относительно их состояний равновесия, убеждаемся, что система (2.7) не имеет предельных циклов.
В данной дипломной работе построены два класса квадратичных двумерных стационарных систем при условии, что частными интегралами являются кривые второго и первого порядков. При этом коэффициенты кривых выражаются через произвольные параметры систем.
Проведено качественное исследование построенных классов систем при фиксированном значении одного из параметров системы. Выведены необходимые и достаточные условия существования у системы двух частных интегралов. В зависимости от условий на коэффициенты были рассмотрены два случая. Найдены состояния равновесия полученных систем, которые принадлежат интегральным кривым. Исследована бесконечно-удалённая часть плоскости систем и доказано отсутствие предельных циклов. Построена качественная картина поведения траекторий систем в круге Пуанкаре.
1 Пуанкаре А. О кривых, определяемых дифференциальными уравнениями.-М.-Л.: ГИТТЛ, 1947. – 839 с.
2 Бендиксон И. О кривых, определяемых дифференциальными уравнениями. – УМН, 1941. – Вып. 9. – 643 с.
3 Биркгоф Дж.Д. Динамические системы. М.-Л.:Гостехиздат, 1941. – 340 с.
4 Еругин Н.П. Построение всего множества систем дифференциальных уравнений, имеющих заданную интегральную кривую. – ПММ. – 1952. – Т.16, Вып. 6. – с. 659–670.
5 Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного исследования динамических систем на плоскости. — М.: Наука, 1976. – 274 с.
6 Серебрякова Н.Н. Качественное исследование одной системы дифференциальных уравнений теории колебаний. – ПММ. – 1963 Т.27, Вып. 1. – 230 с.
7 Черкас Л.А. Об алгебраических решениях уравнения 
8 Яблонский А.И. Алгебраические интегралы одной системы дифференциальных уравнений // Дифференц. уравнения. – 1970. – Т.6, №10. – с. 1752–1760.
9 Филипцов В.Ф. К вопросу алгебраических интегралов одной системы дифференциальных уравнений // Дифференц. уравнения. – 1973. – Т.9, №3. – 256 с.
10 Воробьев А.П. К вопросу о циклах вокруг особой точки типа «узел» // ДАН БССР. – 1960. – Т.4, №9. – 720 с.
http://pandia.ru/text/80/517/18869.php
http://www.bestreferat.ru/referat-110483.html





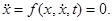
 (1)
(1) , и следовательно,
, и следовательно,  .
. (2)
(2) (3)
(3)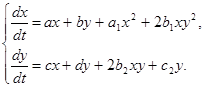
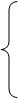
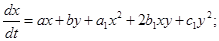
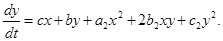
 (1.1)
(1.1)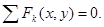
 (1.4)
(1.4) ≠0.
≠0. . (1.9)
. (1.9)
 ,
,