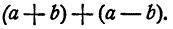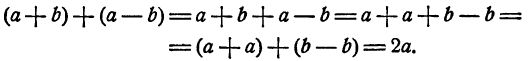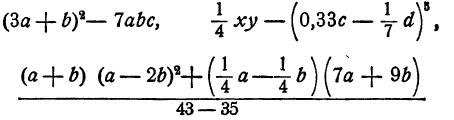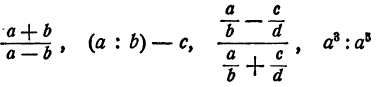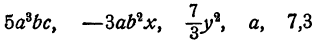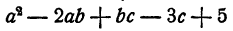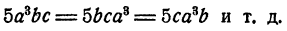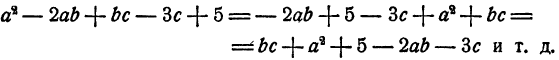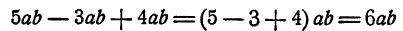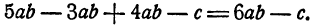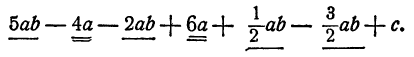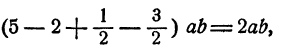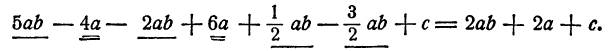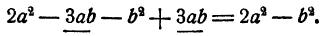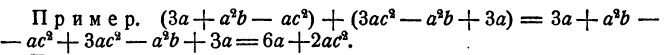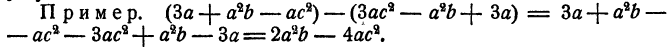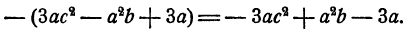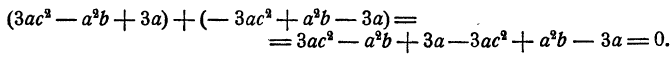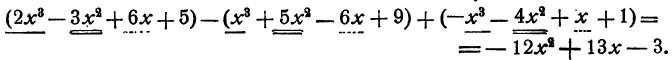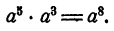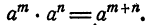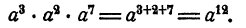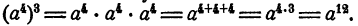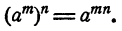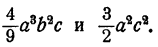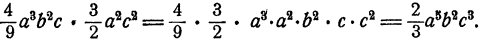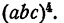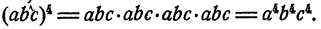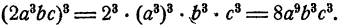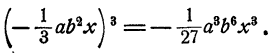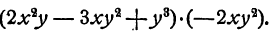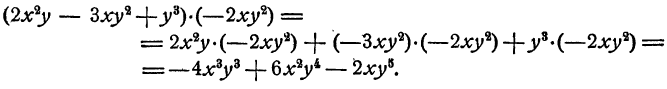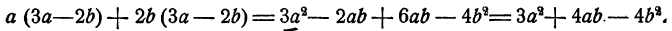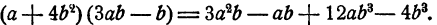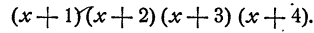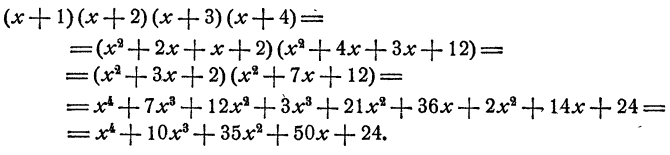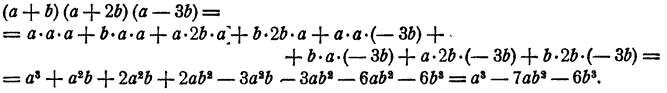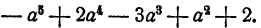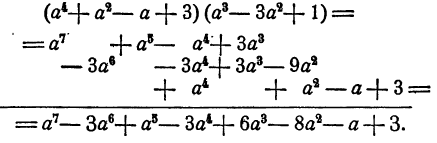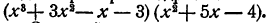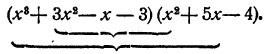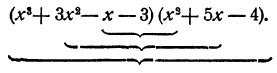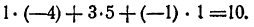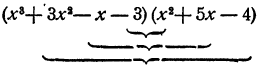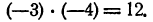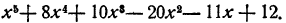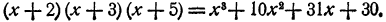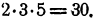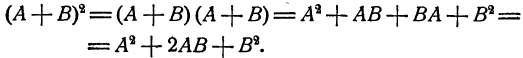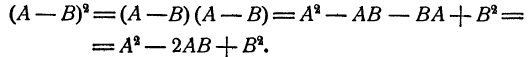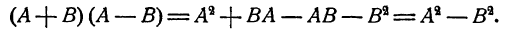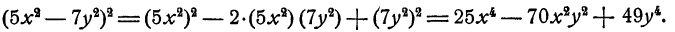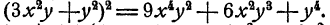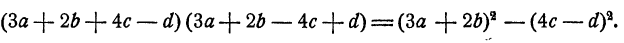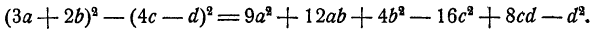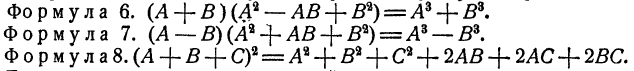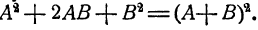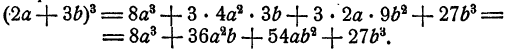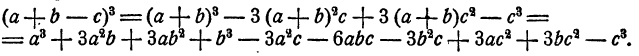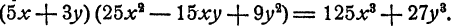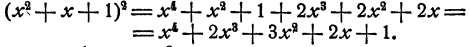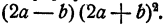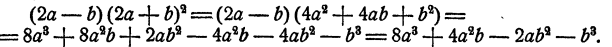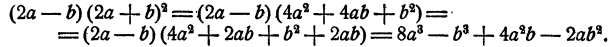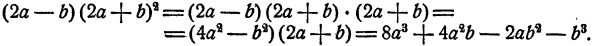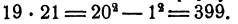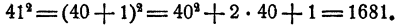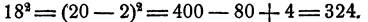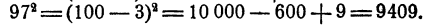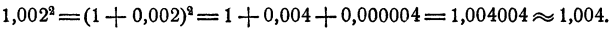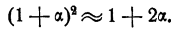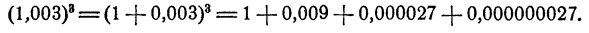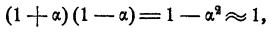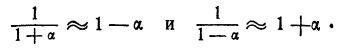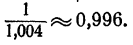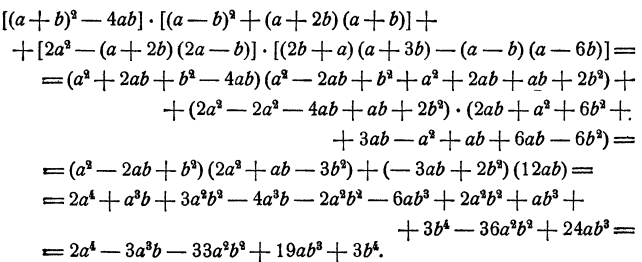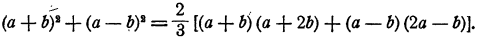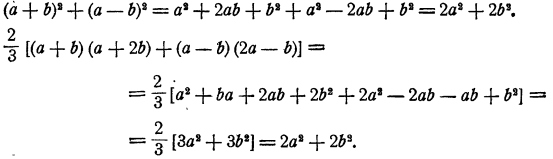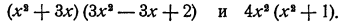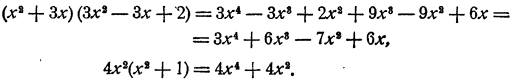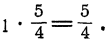Преобразование алгебраических выражений с примерами решения и образцами выполнения
Цель алгебраических преобразований:
При решении задач с помощью алгебры обычно приходится производить арифметические действия над алгебраическими выражениями. Причем непосредственно записанный результат получается в виде нового и часто более сложного выражения.
Пусть, например, требуется к сумме двух чисел а и b прибавить их разность. Записывая указанные действия, мы получим результат в таком виде:
Однако это выражение можно упростить, если воспользоваться
свойствами сложения. Именно, в силу сочетательного и переместительного законов сложения, результат преобразуется так:
Выражения (a + b) + (a — b) и 2a равны тождественно, т. е. равенство между ними справедливо при всех значениях букв а и Ь. Переход от одного алгебраического выражения к другому, тождественно равному ему, называется тождественным преобразованием.
Такого рода преобразования, которые большею частью ведут к упрощению записи результата, почти всегда возможны при действиях над алгебраическими выражениями. Настоящая глава содержит описание приемов, применяемых при’ таких преобразованиях. Этому же вопросу посвящены и две следующие главы.
Типы алгебраических выражений
Определение:
Алгебраические выражения, представляющие собой запись арифметических действий (сложения, вычитания, умножения, деления и возведения в степень), производимых над числами и буквами, называются рациональными алгебраическими выражениями.
Рациональное выражение называется целым, если среди указанных в нем действий нет действия деления на выражение, содержащее буквы. Если же такое действие имеется, то выражение называется дробным. Так, выражения
являются целыми. В последнем примере указано действие деления, но выражение 43 — 35, на которое нужно делить, не содержит букв. В то же время выражения :
являются выражениями дробными.
Заметим, что дробное алгебраическое выражение мажет равняться целому. Так, 
В этой главе мы будем заниматься преобразованием только целых выражений. Среди целых выражений особенно простыми являются так называемые одночлены.
Одночленами называются произведения, составленные из числового множителя (коэффициента) и одной или нескольких букв, каждая из которых взята в некоторой степени.
Числа, выраженные цифрами (т. е. не обозначенные буквами), также причисляются к одночленам. Коэффициенты в одночленах могут быть целыми и дробными, положительными и отрицательными. При записи одночлена принято писать коэффициент впереди множителей, выраженных буквами. Например,
представляют собой одночлены.
Алгебраическая сумма нескольких одночленов называется многочленом. Например,
Одночлены, входящие в многочлен, называются его членами. Говорят, что многочлен составлен из своих членов. Так, многочлен 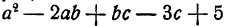
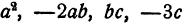
Одночлены целесообразно рассматривать как частный случай многочленов, именно как многочлены, составленные только из одного члена. Многочлены, составленные из двух членов, называются двучленами, из трех членов — трехчленами.
Отметим следующие свойства одночленов и многочленов.
Одночлен не изменяется, если переставить местами множители, из которых он составлен. Например,
Это свойство одночлена непосредственно следует из переместительного закона умножения.
Многочлен не изменяется, если как угодно изменить порядок
его слагаемых. Например,
Справедливость этого свойства следует из переместительного закона сложения.
§ 3. Приведение подобных членов
Рассмотрим многочлен 5аb — 3аb + 4ab — с. Его можно упростить,
так как члены 5аb, —3ab и 4ab отличаются друг от друга только численными коэффициентами. Такие члены можно соединить в один. Действительно, на основании распределительного закона
Члены многочлена, равные или отличающиеся только коэффициентами, называются подобными. Так, члены 5аb, — 3ab и 4ab подобны.
Если многочлен содержит подобные члены, то его можно упростить по следующему правилу: если многочлен содержит несколько подобных членов, то их можно соединить в один, подобный каждому
из них, приняв за его коэффициент алгебраическую сумму
коэффициентов соединяемых членов. Упрощение многочленов по этому правилу называется приведением подобных членов.
Пример:
Привести подобные члены в многочлене
Решение:
В этом примере имеются две группы подобных членов: 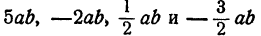
члены второй группы в (- 4+6)a = 2a. Итак,
Правило приведения подобных членов основывается на следующих соображениях. Прежде всего можно на основании переместительного закона расположить члены многочлена так, чтобы все подобные члены оказались рядом. Затем на основании сочетательного закона можно произвести сложение в каждой группе подобных членов. На основании распределительного закона сложение подобных членов сводится к сложению их коэффициентов.
Если многочлен содержит два одночлена, отличающиеся только знаком, то их можно вычеркнуть. Действительно, такие два члена при сложении взаимно уничтожаются, т. е. дают в сумме нуль. Например,
Сложение и вычитание многочленов
Правило. Для того чтобы сложить два или несколько многочленов, нужно сложить все одночлены, из которых эти многочлены составлены.
Затем для упрощения результата следует привести подобные члены.
Правило сложения многочленов непосредственно следует из сочетательного закона сложения.
Правило. Для того чтобы вычесть многочлен из многочлена, нужно к членам уменьшаемого прибавить члены вычитаемого, взятые с противоположными знаками.
Здесь тоже следует .привести подобные члены для упрощения результата.
Правило вычитания многочленов нуждается в некотором пояснении. Мы знаем, что вычесть какое-нибудь число все равно, что прибавить противоположное. Легко видеть, что если некоторое число выражено в виде многочлена, то противоположное ему число равно многочлену, составленному из тех же членов, но взятых с противоположными знаками. Например,
Действительно, два таких многочлена при сложении дают в сумме нуль, так как их члены взаимно умножаются:
Итак, вычесть какой-нибудь многочлен, действительно, все равно, что прибавить многочлен, составленный из тех же членов, но с противоположными знаками.
После того как правила приведения подобных членов, сложения и вычитания многочленов уже освоены, при сложении и вычитании многочленов нет необходимости выписывать промежуточные результаты. Следует сразу писать ответ, осуществляя раскрытие скобок и приведение подобных членов в уме. Например,
При этом нужно аккуратно учитывать знаки коэффициентов. Коэффициенты одночленов, взятых из скобок^ перед которыми стоит знак 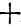
противоположными знаками.
Умножение степеней одной буквы и возведение степени в степень
Пример:
Умножить 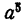
Решение:
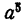
которых равен а. Далее, 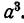
равных а. Следовательно, 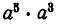
множителей, равных а, т. е.
Также можно рассуждать при любых показателях степени, и мы приходим к следующему правилу.
Правило. Произведение степеней с одинаковыми основаниями
равно степени с тем же основанием и с показателем, равным
сумме показателей.
Короче: при умножении степеней с одинаковыми основаниями показатели складываются. Это правило записывается в виде следующей формулы:
Правило применимо не только к преобразованию произведения двух множителей, являющихся степенями одной буквы, но и к преобразованию произведения любого числа множителей этого вида. Например,
Обратимся теперь к возведению степени в степень.
Пример:
Возвести 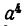
Решение:
Правило. Результат возведения степени в степень равен степени с тем же основанием и с показателем, равным произведению показателей, участвующих в действии.
Короче: при возведении степени в степень показатели перемножаются. Правило записывается следующей формулой:
Умножение одночленов
Пример:
Перемножить одночлены
Решение:
Мы решили пример следующим образом. Сначала на основании переместительного закона умножения мы изменили порядок множителей так, что коэффициенты оказались рядом и степени одинаковых букв оказались рядом. После этого на основании сочетательного закона умножили коэффициенты и умножили степени с одинаковыми основаниями.
Таким же образом мы можем выполнить умножение любых одночленов.
Правило. Чтобы перемножить два (или больше) одночлена, нужно перемножить их коэффициенты и затем приписать каждую букву, входящую в умножаемые одночлены, с показателем, равным сумме показателей, с которыми эта буква входит в одночлены. Если какая-либо буква входит только в один одночлен, переписать ее с тем же показателем.
Возведение одночлена в степень
Пример:
Решение:
Так же производится возведение в степень с любым показателем произведения, составленного из любого числа множителей.
Именно, степень произведения нескольких чисел равна произведению степеней множителей с тем же показателем.
Это правило легко применяется к возведению в степень любого одночлена.
Пример:
Конечно, при возведении одночлена в степень нет необходимости записывать промежуточный результат. Следует сразу писать ответ.
Пример:
Умножение многочлена на одночлен
Пример:
Решение:
Здесь нужно умножить сумму чисел 
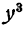
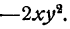
Точно таким же образом можно поступать всегда при умножении многочлена на одночлен. Мы пришли к следующему правилу.
Для того чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить на этот одночлен и результаты сложить.
Конечно, после некоторой тренировки нет необходимости записывать промежуточный результат. Следует писать ответ сразу, выполняя умножение одночленов в уме.
Пример:
Замечание:
Если многочлен не содержит подобных членов, то и при умножении его на любой одночлен получится многочлен, не содержащий подобных членов. Таким образом, при умножении многочлена на одночлен приведение подобных членов в результате умножения невозможно, если только его нельзя было сделать еще до умножения.
Умножение многочлена на многочлен
Пример:
Перемножить многочлены а+2b и За— 2b.
Решение:
Всякий многочлен, в частности многочлен За— 2b , выражает запись результата определенных действий над числами и в конце концов обозначает некоторое число. Поэтому при умножении суммы на это число можно пользоваться распределительным законом
Дальнейшие преобразования сводятся к знакомым для нас действиям— умножению многочлена на одночлен и сложению одночленов. Продолжая вычисления, получим
Сделаем еще один пример, на этот раз не прерывая выкладки рассуждениями.
Пример:
Мы приходим к следующему правилу:
Правило 1. Для того чтобы умножить многочлен на многочлен, нужно каждый член первого множителя умножить на второй множитель, и сложить получившиеся результаты.
Умножение членов первого многочлена на второй можно произведи сразу, и это действие сводится к умножению членов первого многочлена на все члены второго. Таким образом, мы приходим к следующему правилу.
Правило 2. Для того чтобы перемножить два многочлена, нужно каждый член первого многочлена умножить на каждый член второго многочлена и результаты сложить.
Второе правило умножения многочленов сокращает запись по сравнению с первым. Рекомендуется, однако, сначала пользоваться первым правилом и переходить ко второму, когда первое правило уже освоено.
Правила умножения многочленов можно применять и к умножению равных многочленов, т. е. к возведению многочлена в квадрат.
Например,
Умножение нескольких многочленов
Умножение нескольких многочленов следует производить постепенно, объединяя множители каким-либо способом по два. Пример:
Расстановку квадратных скобок можно было, конечно, не делать, а сразу приступить к умножению первых двух множителей.
Пример:
Выполним умножение, объединив первый множитель со вторым, третий с четвертым:
Можно сразу производить умножение нескольких многочленов, руководствуясь следующим правилом:
Чтобы умножить несколько многочленов, нужно составить всеми возможными способами произведения членов, взятых по одному из всех перемножаемых многочленов, и сложить полученные результаты.
Приведем один пример на это правило с подробной записью:
Однако при пользовании этим правилом легко ошибиться, пропустив какую-нибудь комбинацию членов перемножаемых многочленов. Поэтому этим правилом следует пользоваться только в самых простых случаях, например при перемножении двучленов.
Умножение многочленов, содержащих одну букву
Члены многочлена, содержащего одну букву, целесообразно располагать в порядке убывания показателей степеней, с которыми эта буква в него входит. При этом если многочлен содержит так называемый свободный член, т. е. слагаемое, не содержащее букв, то его следует поставить на последнем месте. Например, многочлен 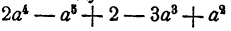
убывающим степеням принимает вид
Член многочлена, содержащий наибольшую степень буквы, называется старшим членом многочлена. Показатель степени в старшем члене называется степенью многочлена. Так, старший член многочлена 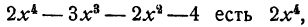
состоящие только из свободного члена, т. е. числа, выраженные цифрами, являются многочленами нулевой степени.
Очевидно, что при умножении многочлена, расположенного по
убывающим степеням, на какой-либо одночлен, зависящий от
той же буквы, получается в результате многочлен, также расположенный по убывающим степеням.
При умножении двух расположенных многочленов целесообразно подписывать результаты умножения отдельных членов одного
многочлена на другой друг под другом, сдвигая начало записи так, чтобы подобные члены оказывались в одном столбце. В случае, если степени идут не подряд, следует оставлять между соответствующими одночленами пустые места, так как может оказаться, что, хотя в первой строке одночлен, содержащий некоторую степень буквы, отсутствует, в других строках появятся одночлены этой степени. Пример:
При такой записи умножение многочленов становится похожим на умножение многозначных чисел.
Заметим, что из правила умножения многочленов следует, что старший член произведения двух многочленов равен произведению старших членов множителей. Следовательно, степень произведения двух многочленов равна сумме степеней множителей. Так, при умножении многочлена пятой степени на многочлен третьей степени мы получим многочлен восьмой степени.
При умножении многочленов не очень высокой степени рекомендуется еще один способ, при котором, результат можно писать сразу, без записи промежуточных результатов. При пользовании этим способом некоторые несложные вычисления приходится производить в уме.
Рассмотрим один пример с подробным объяснением порядка действий.
Пример:
Решение:
Старший член произведения данных многочленов равен произведению их старших членов
Далее, в произведение могут входить члены, содержащие 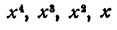
Члены, содержащие 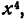
Здесь соединены скобками все те слагаемые данных многочленов, при умножении которых получаются члены, содержащие 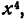
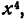
Члены, содержащие 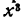
Следовательно, коэффициент при 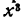
Коэффициент при 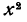
равен . Наконец, свободный член равен 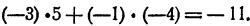
Итак, произведение равно
Ответ.
Конечно, при пользовании этим приемом не нужно переписывать произведение 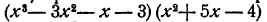
В особенно простых случаях описанный прием можно применять и при умножении нескольких многочленов.
Пример:
В последнем примере мы сразу записали результат умножения, воспользовавшись общим правилом умножения многочленов (§ 10): чтобы умножить многочлены, нужно составить всеми возможными способами произведения их членов, взятых по одному из каждого множителя, и сложить полученные результаты. Старший член произведения равен произведению старших членов множителей и, следовательно, равен 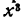
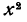
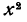
Далее, х в первой степени получается при умножении первого слагаемого из одной скобки на вторые слагаемые из остальных двух. Поэтому коэффициент при x равен 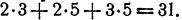
Сокращенное умножение по формулам
При умножении многочленов часто повторяются некоторые типичные случаи, которые следует запомнить.
Формула 1.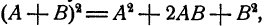
Доказательство:
Формула 2. 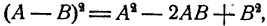
Доказательство:
Формула 3. 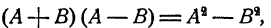
суммы двух чисел на их разность равно разности квадратов этих чисел.
Доказательство:
Рассмотрим несколько примеров на применение этих формул к умножению многочленов. При пользовании формулами следует помнить, что А и В в формулах обозначают любые числа, и в частности, эти числа могут быть выражены в виде одночленов или многочленов.
Пример:
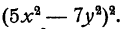
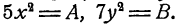
Выписывать промежуточный результат с такой подробностью нет необходимости. По мере развития навыков в пользовании формулами нужно привыкать к возможно более краткой записи.
Пример:
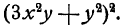
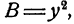
Пример:
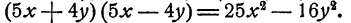
Рассмотрим теперь более сложный пример.
Пример:
(За + 2b + 4c — d) (За+ 2b — 4с +d). Здесь прежде всего можно применить формулу 3, полагая А = 3а+2b;В = 4с — d. Сделав это, получим
А теперь можно применить формулы 1 и 2 для дальнейших преобразований. Получим
Несколько реже, но все же достаточно часто приходится пользоваться еще следующими формулами.
Формула4. 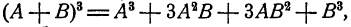
Формула 5. 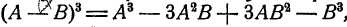
Доказательства этих формул необходимо произвести самим учащимся.
Формула 6 читается так: произведение суммы двух чисел на неполный квадрат их разности равно сумме кубов этих чисел. Здесь «неполным квадратом разности» чисел А и В названо выражение 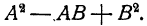
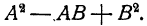
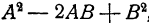
Таким же образом выражение 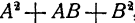
Так что формула 7 читается так: произведение разности двух чисел на неполный квадрат их суммы равно разности кубов этих чисел.
Наконец формула 8 читается так: квадрат суммы нескольких чисел равен сумме их квадратов плюс всевозможные удвоенные произведения этих чисел, взятых по два.
Рассмотрим несколько примеров на. применение формул 4—8.
Пример:
Пример:
Пример:
Здесь результат пишется сразу, как только обнаружено, что второй множитель 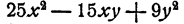
Пример:
Здесь применена формула 8.
Пример:
Решение:
Решим этот пример тремя способами:
Здесь мы сначала преобразовали 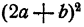
Здесь мы разбили квадрат суммы 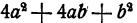
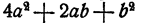
Способ 3.
В заключение обзора формул сделаем следующее, общее замечание. Всякое преобразование произведения многочленов, которое совершается при помощи формул 1—8, может быть проведено и без применения формул, посредством общих правил умножения многочлена на многочлен. Формулы 1—8 позволяют только в некоторых случаях упростить и сократить вычисления. Поэтому, формулы 1—8 называют формулами сокращенного умножения.
Применение формул сокращенного умножения к устным вычислениям
Формулы сокращенного умножения применяются не только к умножению многочлена на многочлен. Они с успехом могут быть применены к многим вычислениям над числами. Рассмотрим несколько таких примеров.
Пример:
Вычислить 19 • 21
Решение:
Достаточно заметить, что 19 = 20 — 1 и 21 = 20+1, чтобы, воспользовавшись формулой 3, сразу сказать результат. Именно,
Пример:
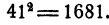
Решение:
При помощи формулы 1
Пример:
Пример:
Таким образом, формулы сокращенного умножения удобно применять:
- При умножении чисел, представляющих собой сумму и разность двух чисел, каждое из которых легко возвести в квадрат.
- При возведении в квадрат двузначных чисел, близких к «круглым» числам.
Покажем некоторые другие применения. Часто приходится возводить в квадрат числа, очень близкие к единице, причем результат нужно знать приближенно с тем же числом знаков после запятой, с которым дано число, возводимое в квадрат. Например,
Обобщая эти два примера, приходим к следующему выводу. Если а есть очень маленькое по абсолютной величине число, положительное или отрицательное, то
Точное равенство имеет вид 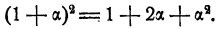
меньше абсолютной величины а во столько же раз, во сколько абсолютная величина а меньше 1. Поэтому, если а очень мало по абсолютной величине, то 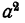
Таким же образом из формулы для куба суммы мы получим приближенную формулу для куба числа, близкого к единице. Именно,
Посмотрим на примере, насколько эта формула точна.
Пример:
Последние два слагаемых исчезающе малы по сравнению с первыми, так что действительно 
Наконец,, формула 3 дает при малых а следующий результат:
Например,
Некоторые выводы
Мы условились рассматривать одночлены как частный случай многочленов, именно как многочлены, составленные из одного члена. Воспользуемся этим соглашением и сделаем следующие выводы:
- Сумма и разность двух многочленов есть многочлен.
- Произведение двух многочленов есть многочлен.
А из этих выводов непосредственно следует такая общая теорема:
Всякое целое алгебраическое выражение равно некоторому многочлену.
Или, что то же самое:
Всякое целое алгебраическое выражение может быть преобразовано к виду многочлена.
Действительно, целое алгебраическое выражение есть запись действий сложения, вычитания и умножения (в том числе и умножения равных множителей, т. е. возведения в степень) над числами, часть которых обозначена буквами. Как заданные числа, так и отдельные буквы представляют собой одночлены.
Произведя над ними одно за другим указанные действия, мы будем получать результаты в виде многочленов в силу сформулированных выше выводов. И, наконец, окончательный результат тоже будет иметь вид многочлена, что и требовалось доказать. Например,
Заметим еще, что всякий многочлен равен некоторому
приведенному многочлену, т. е. многочлену, не содержащему подобных членов. Действительно, если многочлен содержит подобные члены, то их можно привести. В силу этого всякое целое алгебраическое выражение можно преобразовать к виду приведенного многочлена.
Цепочка тождественных преобразований называется алгебраической выкладкой. Таким образом, в настоящей главе даны правила проведения выкладки, посредством которой всякое целое алгебраическое выражение может быть преобразовано к виду приведенного многочлена.
Очевидно, что если два приведенных многочлена составлены из одинаковых одночленов, то они равны тождественно, т. е. их значения равны при всех численных значениях входящих в них букв. Верна также и обратная теорема:
Теорема о тождестве. Если два приведенных
многочлена равны тождественно, та они составлены из oдинаковых одночленов.
Доказательство теоремы о тождестве довольно сложно и выходит за рамки курса элементарной алгебры.
Эти две теоремы дают возможность ответить на такой вопрос. Пусть даны два целых алгебраических выражения. Равны они тождественно или нет? Для решения этого вопроса достаточно привести каждое из выражений к виду приведенного многочлена. Если при этом окажется, что полученные многочлены составлены из одинаковых одночленов, то данные выражения тождественно равны. Если же полученные многочлены окажутся различными, т. е. составленными из неодинаковых одночленов, то данные выражения не равны тождественно.
Пример:
Решение:
После преобразований выражение, находящееся в левой части равенства, оказалось равным 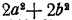
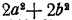
Пример:
Рассмотрим два выражения
Они имеют ряд одинаковых значений. Действительно, при х = 0 они оба равны нулю; при х = 1 каждое из них равно 4 • 2 = 8; при х = 2 первое равно 10 • 8 = 80, второе равно 16 • 5 = 80; при х = 3 первое равно 18 • 20 = 360,
второе 36 • 10 = 360. Может быть они равны тождественно? Для выяснения этого вопроса раскроем скобки:
Таким образом, данные выражения преобразуются в различные приведенные многочлены, и следовательно, они не могут равняться тождественно. И действительно, они принимают различные значения, например при 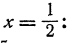
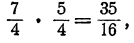
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Равносильные уравнения, преобразование уравнений
Некоторые преобразования позволяют нам перейти от решаемого уравнения к равносильным, а также к уравнениям-следствиям, благодаря чему упрощается решение первоначального уравнения. В данном материале мы расскажем, что из себя представляют эти уравнения, сформулируем основные определения, проиллюстрируем их наглядными примерами и поясним, как именно осуществляется вычисление корней исходного уравнения по корням уравнения-следствия или равносильного уравнения.
Понятие равносильных уравнений
Равносильными называются такие уравнения, имеющие одни и те же корни, или же те, в которых корней нет.
Определения такого типа часто встречаются в различных учебниках. Приведем несколько примеров.
Уравнение f ( x ) = g ( x ) считается равносильным уравнению r ( x ) = s ( x ) , если у них одинаковые корни или у них обоих нет корней.
Уравнения с одинаковыми корнями считаются равносильными. Также ими считаются два уравнения, одинаково не имеющие корней.
Если уравнение f ( x ) = g ( x ) имеет то же множество корней, что и уравнение p ( x ) = h ( x ) , то они считаются равносильными по отношению друг к другу.
Когда мы говорим о совпадающем множестве корней, то имеем в виду, что если определенное число будет корнем одного уравнения, то оно подойдет в качестве решения и другому уравнению. Ни одно из уравнений, являющихся равносильными, не может иметь такого корня, который не подходит для другого.
Приведем несколько примеров таких уравнений.
Например, равносильными будут 4 · x = 8 , 2 · x = 4 и x = 2 , поскольку каждое из них имеет только один корень – двойку. Также равносильными будут x · 0 = 0 и 2 + x = x + 2 , поскольку их корнями могут быть любые числа, то есть множества их решений совпадают. Также равносильными будут уравнения x = x + 5 и x 4 = − 1 , каждое из которых не имеет ни одного решения.
Для наглядности рассмотрим несколько примеров неравносильных уравнений.
К примеру, таковыми будут x = 2 и x 2 = 4 , поскольку их корни отличаются. То же относится и к уравнениям x x = 1 и x 2 + 5 x 2 + 5 , потому что во втором решением может быть любое число, а во втором корнем не может быть 0 .
Определения, данные выше, подойдут и для уравнений с несколькими переменными, однако в том случае, когда мы говорим о двух, трех и более корнях, более уместно выражение «решение уравнения». Таким образом, подытожим: равносильные уравнения – это те уравнения, у которых одни и те же решения или их совсем нет.
Возьмем примеры уравнений, которые содержат несколько переменных и являются равносильными друг другу. Так, x 2 + y 2 + z 2 = 0 и 5 · x 2 + x 2 · y 4 · z 8 = 0 включают в себя по три переменных и имеют только одно решение, равное 0 , во всех трех случаях. А пара уравнений x + y = 5 и x · y = 1 равносильной по отношению друг к другу не будет, поскольку, например, значения 5 и 3 подойдут для первого, но не будут решением второго: при подстановке их в первое уравнение мы получим верное равенство, а во второе – неверное.
Понятие уравнений-следствий
Процитируем несколько примеров определений уравнений-следствий, взятых из учебных пособий.
Следствием уравнения f ( x ) = g ( x ) будет уравнение p ( x ) = h ( x ) при условии, что каждый корень первого уравнения будет в то же время корнем второго.
Как решать квадратные уравнения
О чем эта статья:
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x 2 — 2x + 6 = 0
- x 2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
- 2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: | |
|---|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам. Как решить уравнение ax 2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0. Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0. Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Разделим обе части на 8: Ответ: уравнение 8x 2 + 5 = 0 не имеет корней. Как решить уравнение ax 2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение: Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня: Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0 0,5x = 0,125, Ответ: х = 0 и х = 0,25. Как разложить квадратное уравнениеС помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так: Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2). Дискриминант: формула корней квадратного уравненияЧтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так: где D = b 2 − 4ac — дискриминант квадратного уравнения. Эта запись означает: Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться. Алгоритм решения квадратных уравнений по формулам корнейТеперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни. В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней. Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться! Примеры решения квадратных уравненийКак решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике. Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5. Пример 2. Решить уравнение 54 — 6x 2 = 0.
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую Ответ: два корня 3 и — 3. Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1. Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7. Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112 Ответ: корней нет. В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся. Формула корней для четных вторых коэффициентовРассмотрим частный случай. Формула решения корней квадратного уравнения Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней: 2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″> Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид: где D1 = n 2 — ac. Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения. Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Формула ВиетаЕсли в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства: Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам. Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0. Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре: Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит: Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента: Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное. Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется: Результат проделанных вычислений в том, что мы убедились в справедливости выражения: Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она: Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0. Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение. Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″> Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы. Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже. Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам: Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p> Упрощаем вид квадратных уравненийЕсли мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту. Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0. Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100. Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов. Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто. А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0. Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0. Связь между корнями и коэффициентамиМы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты: Из этой формулы, можно получить другие зависимости между корнями и коэффициентами. Например, можно применить формулы из теоремы Виета: Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3. Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: источники: http://zaochnik.com/spravochnik/matematika/systems/ravnosilnye-uravnenija-preobrazovanie-uravnenij/ http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya |