Презентация тригонометрические формулы и уравнения

Применение тригонометрических формул для решения уравнений. Часть 1
презентация к уроку по алгебре (10 класс) на тему

Данный материал предназначен для изучения, закрепления решения тригонометрических уравнений с применением тригонометрических формул. Презентация может быть использована для подготовки учащихся к сдаче экзамена профильной математики. Она может помочь учащимся к самостоятельной подготовке к экзамену или контрольной работе по теме «Решение тригонометрических уравнений». Презентация содержит типичные уравнения и пути их решения.

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Применение тригонометрических формул для решения уравнений Часть I НОЧУ «Британская международная школа» Пестова Ю.В.

sin2x – cosx = 0 2sinxcosx – cosx = 0 cosx (2sinx – 1) = 0 cosx = 0 , sinx = ½ ;… Решим уравнение: sin2x = 2sinxcosx Найдите x

Решим уравнение: cos7x + cosx = 0 2cos4xcos3x = 0 cos4x = 0, cos3x = 0;… cosα + cosβ = = 2cos cos α+β 2 α-β 2 Найдите x

Решим уравнение: sinx + sin5x = 0 2sin3xcos2x = 0 sin3x = 0, cos2x = 0;… sinα + sinβ = = 2sin cos α+β 2 α-β 2 Найдите x

Решим уравнение: sin4xcos2x – cos4xsin2x = sin(α-β) = sinαcosβ — cosαsinβ √ 2 2 sin2x = √ 2 2 Решим уравнение: cosxcos3x – sin3xsinx = — cos(α+β) = cosαcosβ — sinαsinβ √ 3 2 cos4x = — √ 3 2 Найдите x Найдите x

Решим уравнение: sin 2 3x + cox 2 3x + sin3x = 2 sin 2 x + cos 2 x = 1 1 + sin3x = 2 sin3x = 1 Найдите x Решим уравнение: = 5 cos 2 x 1 cos 2 x 1 1 + tg 2 x = tg 2 x = 4 tgx = ± 2 Найдите x

Решим уравнение: 1– 2cos 2 2x = – √ 2 2 cos2α = 2cos 2 α – 1 – cos2x = – √ 2 2 cos2x = √ 2 2 Найдите x

Решим уравнение: 2sin 2 x = 1/3 sin 2 α = 1 – cos2α 2 1 – cos2x = 1/3 cos2x = 2/3 Найдите x

По теме: методические разработки, презентации и конспекты

решение тригонометрических уравнений с применением тригонометрических формул

конспект урока в 10 классе и презентация к нему по теме «решение тригонометрических уравнений с помощью тригонометрических формул». Цели урока: знакомство обучающихся со способами решения тригонометри.

Учебно-методическое пособие «Решение уравнений». Часть 1: Решение иррациональных уравнений.

Электронное учебно-методическое пособие для уроков повторения в 11 классе по теме «Решение уравнений».

Урок 10 класс «Применение тригонометрических формул к преобразованию выражений»

Применение тригонометрических формул к преобразованию выражений.

Тема: Применение тригонометрических формул к решению уравнений.

Цели и задачи:повторить формулы корней простейших тригонометрических уравнений;повторить основные тригонометрические формулы;рассмотреть методы решения тригонометрических с применением тригонометричес.

Применение тригонометрических формул для решения уравнений. Часть 2

Данный материал предназначен для изучения, закрепления решения тригонометрических уравнений с применением тригонометрических формул. Презентация может быть использована для подготовки учащихся к сдаче.

Опорный конспект по теме «Применение тригонометрических формул»

В данной разработке приведены тригонометрические формулы и на примерах показано их применение для разных типов задач.

Разработка мультимедийного урока на тему: «Применение тригонометрических формул».

Цель: развитие навыков упрощения и вычисления выражений с применением тригонометрических тождеств.План урока:1.организационный момент;2.история тригонометрии;3.работа в группах;4.задачи с подробным оф.

Презентация на тему : Методы решений тригонометрических уравнений.

Данная презентация предназначена для повторения и закрепления решений тригонометрических уравнений в 10-11 классах,в которой повторяются формулы тригонометрии и приведены примеры решений уравнений. Презентация может быть использована при подготовке к ЕГЭ (ПРОФИЛЬНЫЙ УРОВЕНЬ №13).

Просмотр содержимого документа
«Презентация на тему : Методы решений тригонометрических уравнений.»

Методы решения тригонометрических уравнений

• Метод замены переменной
• Метод разложения на множители
• Однородные тригонометрические уравнения
• С помощью тригонометрических формул:

• Формул сложения
• Формул приведения
• Формул двойного аргумента

Метод замены переменной

С помощью замены t = sinx или t = cosx, где t ∈ [−1;1] решение исходного уравнения сводится к решению квадратного или другого алгебраического уравнения.

См. примеры 1 – 3

Иногда используют универсальную тригонометрическую подстановку: t = tg

Метод разложения на множители

Суть этого метода заключается в том, что произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а другие при этом не теряют смысл:

f(x) · g(x) · h(x) · … = 0 ⟺ f(x) = 0 или g(x) = 0 или h(x) = 0

и т.д. при условии существования каждого из сомножителей

См. примеры 4 – 5

Однородные тригонометрические уравнения

Уравнение вида a sin x + b cos x = 0 называют однородным тригонометрическим уравнением первой степени .

a sin x + b cos x = 0

a sin x b cos x 0

Деление на cos x допустимо, поскольку решения уравнения cos x = 0 не являются решениями уравнения a sin x + b cos x = 0 .

Однородные тригонометрические уравнения

Уравнение вида a sin 2 x + b sin x cos x + c cos 2 x = 0 называют однородным тригонометрическим уравнением второй степени .

a sin 2 x + b sin x cos x + c cos 2 x = 0

a sin 2 x b sin x cos x c cos 2 x 0

a tg 2 x + b tg x + c = 0

Далее, вводим новую переменную tg x = t и решаем методом замены переменной.

Замечание. Если в данном уравнении а = 0 или с = 0 то, уравнение решается методом разложения

С помощью тригонометрических формул

cos (x − y) = cosx cosy + sinx siny

С помощью тригонометрических формул

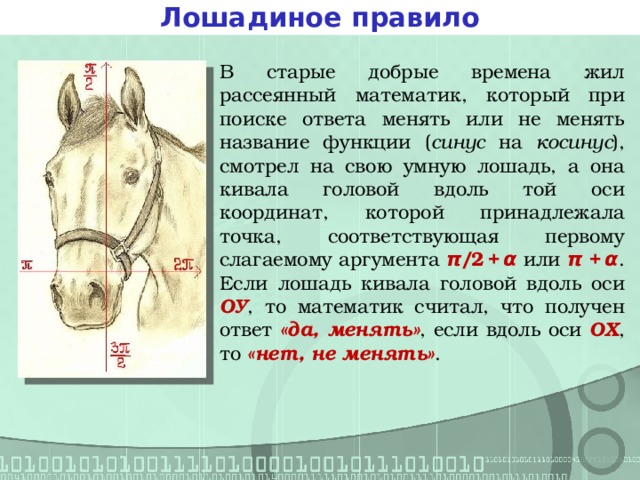
В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции ( синус на косинус ), смотрел на свою умную лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/ 2 + α или π + α .

Если лошадь кивала головой вдоль оси ОУ , то математик считал, что получен ответ «да, менять» , если вдоль оси ОХ , то «нет, не менять» .

С помощью тригонометрических формул

3. Формулы двойного аргумента :

Презентация по алгебре на тему «Решение тригонометрических уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Выполнила: учитель математики Гадирова Н.Я. МБОУ «Лицей № 4» г.о. Королев Методика решения тригонометрических уравнений L/O/G/O

Решение тригонометрических уравнений Для тригонометрических уравнений применимы общие методы решения (разложение на множители, замена переменной, функционально-графические) и равносильные преобразования общего характера.

Основы тригонометрии, как и основы алгебры и начал анализа закладываются в школе. Тригонометрические функции начинают изучать в 8 классе на уроках геометрии и продолжают в 10-11 классах. Тригонометрические уравнения слишком разнообразны для того, чтобы попытаться дать их общую классификацию или общий метод решения. Мы можем указать лишь способы решения некоторых типов таких уравнений.

Методы решения тригонометрических уравнений Основные методы: замена переменной, разложение на множители, однородные уравнения, прикладные методы: по формулам преобразования суммы в произведение и произведения в сумму, по формулам понижения степени, универсальная тригонометрическая подстановка введение вспомогательного угла, умножение на некоторую тригонометрическую функцию.

1.Потеря корней: делим на g(х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2. Лишние корни: возводим в четную степень. умножаем на g(х) (избавляемся от знаменателя). Этими операциями мы расширяем область определения. Проблемы ,возникающие при решении тригонометрических уравнений

Наша задача: свести любое тригонометрическое уравнение к простейшему виду.

Решение простейших тригонометрических уравнений

Формулы корней простых тригонометрических уравнений 1.cost = а , где |а| ≤ 1 или Частные случаи 1)cost=0 t = π/2+πk‚ kЄZ 2)cost=1 t = 0+2πk‚ kЄZ 3)cost = -1 t = π+2πk‚ kЄZ 2.sint = а, где | а |≤ 1 или Частные случаи 1)sint=0 t = 0+πk‚ kЄZ 2)sint=1 t = π/2+2πk‚ kЄZ 3)sint = — 1 t = — π/2+2πk‚ kЄZ 3. tgt = а, аЄR t = arctg а + πk‚ kЄZ 4. ctgt = а, аЄR t = arcctg а + πk‚ kЄZ

Your Text Here Yor Text Here При повторении формул решения уравнений следует обратить внимание на то, что формулы задают множества чисел, которые образованы по закону арифметической прогрессии с разностью 2π или π. С другой стороны использование общей формулы серий решений не всегда является удобной при отборе корней, в частности, на числовой окружности. В этом случае как раз удобнее не объединять серии решений тригонометрических уравнений, а представлять их совокупностью, выделяя разность 2π соответствующих прогрессий.

Your Text Here Yor Text Here sin x

Yor Text Here cos x

Yor Text Here tg x и ctg x

Решение простейших уравнений tg2x = -1 2x = arctg (-1) + πk, kЄZ 2x = -π/4 + πk, kЄZ x = -π/8 + πk/2, kЄZ Ответ: -π/8 + πk/2, kЄZ. 2) cos(x+π/3) = ½ x+π/3 = ±arccos1/2 + 2πk, kЄZ x+π/3 = ±π/3 + 2πk, kЄZ x = -π/3 ± π/3 + 2πk, kЄZ Ответ: -π/3 ± π/3 + 2πk, kЄZ 3) sin(π – x/3) = 0 упростим по формулам приведения sin(x/3) = 0 частный случай x/3 = πk, kЄZ x = 3πk, kЄZ. Ответ: 3πk, kЄZ.

Решение тригонометрических уравнений разложением на множители. Метод разложения на множители заключается в следующем: если То всякое решение уравнения Является решением совокупности уравнений Обратное утверждение, неверно: не всякое решение совокупности уравнений (2) является решением уравнения (1). Это объясняется тем, что решения отдельных уравнений (2) могут не входить в область определения функции .Поэтому, если при решении тригонометрического уравнения методом разложения на множители, функции, входящие в уравнение, определены не для всех значений аргумента, после нахождения решения должна быть сделана проверка, чтобы исключить лишние корни. Можно поступать другим способом: находить область допустимых значений исходного уравнения и выбирать только те корни, которые входят в найденную область допустимых значений

Решение тригонометрических уравнений разложением на множители.

Решение тригонометрических уравнений , сводящихся к квадратным. При решении уравнений указанного типа в основном применяются следующие тригонометрические тождества: Уравнения сводимые к квадратным a∙sin²x + b∙sinx + c=0 Пусть sinx = p, где |p| ≤1, тогда a∙p² + b∙p + c = 0 Найти корни, вернуться к замене и решить простые уравнения.

Решение тригонометрических уравнений , сводящихся к квадратным. Пример 1. Решить уравнение 2 sin2x + sinx — 1 = 0. Решение. Введём новую переменную t = sinx. Тогда данное уравнение примет вид 2t2 + t — 1 = 0. Решим его: D = 1 + 8 = 9, Cледовательно, sinx = 1/2 или sinx = -1.

2) sinx = -1, 1) sinx = 1/2,

Решение уравнений, однородных относительно синуса и косинуса в которых сумма показателей степеней у sinx и cosx (степень уравнения) во всех членах уравнения одинакова. Например,

Однородные тригонометрические уравнения 2.Однородные 1)Первой степени: a∙sinx + b∙cosx = 0 Т.к. sinx и cosx одновременно не равны нулю, то разделим обе части уравнения на cosx. Получим: простое уравнение a∙tgx + b = 0 или tgx = m 2)Второй степени: a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0 Разделим обе части на cos²x. Получим квадратное уравнение: a∙tg²x + b∙tgx + c = 0. В частности, уравнения вида приводятся к однородным путем представления правой части в виде:

Решение уравнений с помощью введения вспомогательного аргумента. Рассмотрим уравнение Разделим левую и правую часть уравнения на : Так как то существует угол φ такой, что при этом Тогда уравнение примет вид и выбор будут не всегда равносильны. Отметим, что к выбору угла φ в задачах с параметрами нужно относиться внимательно: выбор Решите уравнения:

Уравнения, линейные относительно sin x и cos x а sin x + в cos x = с. Если а=в=0, а с не равно 0, то уравнение теряет смысл; Если а=в=с=0, то х – любое действительное число, то есть уравнение обращается в тождество. Рассмотрим случаи, когда а,в,с не равны 0. Примеры: 3 sin 5x — 4 cos 5x = 2 2 sin 3x + 5 cos 3x = 8. Последнее уравнение не имеет решений, так как левая часть его не превосходит 7. Уравнения, этого вида можно решить многими способами: с помощью универсальной подстановки, выразив sin x и cos x через tgх ; сведением уравнения к однородному; введением вспомогательного аргумента и другими. Решение этих уравнений существует при

Решение уравнений с применением формул понижения степени. : При решении широкого круга тригонометрических уравнений ключевую роль играют формулы понижения степени Решение уравнений с применением формул тройного аргумента. При решении ряда уравнений наряду с другими существенную роль играют формулы (1) (2)

Решение уравнений методом универсальной подстановки. Тригонометрическое уравнение вида где R – рациональная функция, с помощью тригонометрических формул двойного и тройного аргумента, а также формул сложения можно свести к рациональному уравнению относительно аргументов после чего уравнение может быть сведено к рациональному уравнению относительно с помощью формул универсальной тригонометрической подстановки Следует отметить, что применение формул может приводить к сужению ОДЗ исходного уравнения, поскольку не определен в точках поэтому в таких случаях нужно проверять, являются ли углы корнями исходного уравнения.

тригонометрические уравнения, содержащие знак модуля или знак корня. Специфика тригонометрических уравнений, содержащих знак модуля или знак корня, состоит в том, что они сводятся к смешанным системам, где кроме уравнений нужно решать тригонометрические неравенства и из решений уравнений выбирать лишь те, которые удовлетворяют неравенствам. Решите уравнения:

Использование ограниченности функций при решении тригонометрических уравнений. При решении некоторых тригонометрических уравнений часто используется свойство ограниченности функций и , то есть следующие неравенства:

Функциональные методы решения тригонометрических и комбинированных уравнений. Не всякое уравнение f(x)=g(x) в результате преобразований может быть сведено к уравнению того или иного стандартного вида, для которого существует определенный метод решения. В таких случаях оказывается полезным использовать такие свойства функций f(x) и g(x), как монотонность, ограниченность, четность, периодичность и др. Так, если одна из функций убывает, а вторая возрастает на промежутке X, то при наличии у уравнения f(x)=g(x) корня на этом промежутке, этот корень единственный, и тогда его, например, можно найти подбором. Если, далее, функция f(x) на промежутке X ограничена сверху, причем , а функция g(x) ограничена снизу, причем то уравнение f(x)=g(x) равносильно системе уравнении Иногда для решения уравнения f(x)=g(x) можно построить графики функции y=f(x), y=g(x) и определить абсциссы точек пересечения. Также рассматривается применение производной для исследования тригонометрических уравнений.

Способы отбора корней тригонометрических уравнений на заданном промежутке Арифметический способ Перебор значений целочисленного параметра n и вычисление корней Алгебраический способ Перебор значений целочисленного параметра n и вычисление корней Геометрический способ Изображение корней на тригонометрической окружности с последующим отбором с учетом имеющихся ограничений

Арифметический способ Перебор значений целочисленного параметра n и вычисление корней Решить уравнение Записать корни уравнения Разделить виды решения для косинуса; подсчитать значения x при целых n до тех пор, пока значения x не выйдут за пределы данного отрезка. Записать ответ. x k -2 -1 0 1 2 … x k -2 -1 0 1 2 …

Алгебраический способ Решение неравенства относительно неизвестного параметра n и вычисление корней Записать двойное неравенство для неизвестного (x), соответственное данному отрезку или условию; решить уравнение. Для синуса и косинуса разбить решения на два. Подставить в неравенство вместо неизвестного (x) найденные решения и решить его относительно n. Учитывая, что n принадлежит Z, найти соответствующие неравенству значения n. Подставить полученные значения n в формулу корней.

Геометрический способ Изображение корней на тригонометрической окружности с последующим отбором с учетом имеющихся ограничений На окружности Решить уравнение. Обвести дугу, соответствующую данному отрезку на окружности. Разделить виды решений для синуса и косинуса. Нанести решения уравнения на окружность. Выбрать решения, попавшие на обведенную дугу. y x 0 arccos a d -arccos a c а

Геометрический способ Изображение корней на графике с последующим отбором с учетом имеющихся ограничений На графике Решить уравнение. Построить график данной функции, прямую у = а, на оси х отметить данный отрезок. Найти точки пересечения графиков. Выбрать решения, принадлежащие данному отрезку. x y y = sin x y = a arcsin a П-arcsin a с d a

Пример: Найти все корни уравнения которые удовлетворяют условию Решение. 10sin2 x = – cos 2x + 3; 10sin2 x = 2sin2 x – 1 + 3, 8sin2 x = 2; 0 y x С помощью числовой окружности получим:

Выберем корни, удовлетворяющие условию задачи. Из первой серии: Следовательно n=0 или n=1, то есть Из второй серии: Следовательно n=0 или n=1, то есть