При каких натуральных значениях а уравнение

Задачи с параметром

1. Задача.
При каких значениях параметра a уравнение ( a — 1) x 2 + 2 x + a — 1 = 0 имеет ровно один корень?

1. Решение.
При a = 1 уравнение имеет вид 2 x = 0 и, очевидно, имеет единственный корень x = 0. Если a № 1, то данное уравнение является квадратным и имеет единственный корень при тех значениях параметра, при которых дискриминант квадратного трехчлена равен нулю. Приравнивая дискриминант к нулю, получаем уравнение относительно параметра a 4 a 2 — 8 a = 0, откуда a = 0 или a = 2.

1. Ответ: уравнение имеет единственный корень при a О <0; 1; 2>.

2. Задача.
Найти все значения параметра a , при которых имеет два различных корня уравнение x 2 +4 ax +8 a +3 = 0.
2. Решение.
Уравнение x 2 +4 ax +8 a +3 = 0 имеет два различных корня тогда и только тогда, когда D = 16 a 2 -4(8 a +3) > 0. Получаем (после сокращения на общий множитель 4) 4 a 2 -8 a -3 > 0, откуда

a Ц 7 2

или a > 1 +

Ц 7 2

2. Ответ:

a О (- Ґ ; 1 –

Ц 7 2

) И (1 +

Ц 7 2

; Ґ ).

3. Задача.
Известно, что
f 2 ( x ) = 6 x — x 2 -6.
а) Постройте график функции f 1 ( x ) при a = 1.
б) При каком значении a графики функций f 1 ( x ) и f 2 ( x ) имеют единственную общую точку?

3. Решение.
3.а. Преобразуем f 1 ( x ) следующим образом
График этой функции при a = 1 изображен на рисунке справа.
3.б. Сразу отметим, что графики функций y = kx + b и y = ax 2 + bx + c ( a № 0) пересекаются в единственной точке тогда и только тогда, когда квадратное уравнение kx + b = ax 2 + bx + c имеет единственный корень. Используя представление f 1 из 3.а , приравняем дискриминант уравнения a = 6 x — x 2 -6 к нулю. Из уравнения 36-24-4 a = 0 получаем a = 3. Проделав то же самое с уравнением 2 x — a = 6 x — x 2 -6 найдем a = 2. Нетрудно убедиться, что эти значения параметра удовлетворяют условиям задачи. Ответ: a = 2 или a = 3.

4. Задача.
Найти все значения a , при которых множество решений неравенства x 2 -2 ax -3 a і 0 содержит отрезок [3;6].

4. Решение.
Первая координата вершины параболы f ( x ) = x 2 -2 ax -3 a равна x 0 = a . Из свойств квадратичной функции условие f ( x ) і 0 на отрезке [3;6] равносильно совокупности трех систем

м н о

a Ј 3, f (3) = 9-9 a і 0,

м н о

3 a D = 4 a 2 +12 a Ј 0,

м н о

a і 6, f (6) = 36-15 a і 0.

Решением первой системы является множество (- Ґ ,1]. Вторая и третья система решений не имеют.

4. Ответ: a О (- Ґ ,1].

5. Задача (9 кл.)
При каком наименьшем натуральном значении a уравнение

x 2 +2 ax -3 a +7 = 2 x

имеет ровно два решения?

5. Решение.
Перепишем это уравнение в виде x 2 + (2 a -2) x — 3 a +7 = 0. Это квадратное уравнение, оно имеет ровно два решения, если его дискриминант строго больше нуля. Вычисляя дискриминант, получаем, что условием наличия ровно двух корней является выполнение неравенства a 2 + a -6 > 0. Решая неравенство, находим a a > 2. Первое из неравенств, очевидно, решений в натуральных числах не имеет, а наименьшим натуральным решением второго является число 3.

6. Задача (10 кл.)
Найти все значения a , при которых график функции

f ( x ) =

x 2 + | ax +2 | a -1

проходит через точку с координатами (-1;1).

6. Решение.
Из условия f (-1) = 1 имеем уравнение

1 =

1+ | — a +2 | a -1

,

или, после очевидных преобразований, a -2 = | 2- a | . Последнее уравнение равносильно неравенству a і 2.

6. Ответ: a О [2; Ґ ).

7. Задача (10 кл.)
При каких значениях a сумма квадратов корней уравнения

x 2 -2 ax + a 2 — a = 0

больше чем 12?

7. Решение.
Дискриминант уравнения x 2 -2 ax + a 2 — a = 0 равен 4 a . Поэтому действительные корни этого уравнения существуют, если a і 0. Применяя к данному уравнению теорему Виета получаем x 1 + x 2 = 2 a и x 1 · x 2 = a 2 — a . Отсюда x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 -2 x 1 · x 2 = 2 a 2 +2 a . Решениями неравенства 2 a 2 +2 a > 12, удовлетворяющими условию a і 0, являются числа a > 2.

При каких натуральных значениях уравнения имеют более / менее одного корня?

Алгебра | 5 — 9 классы

При каких натуральных значениях уравнения имеют более / менее одного корня?

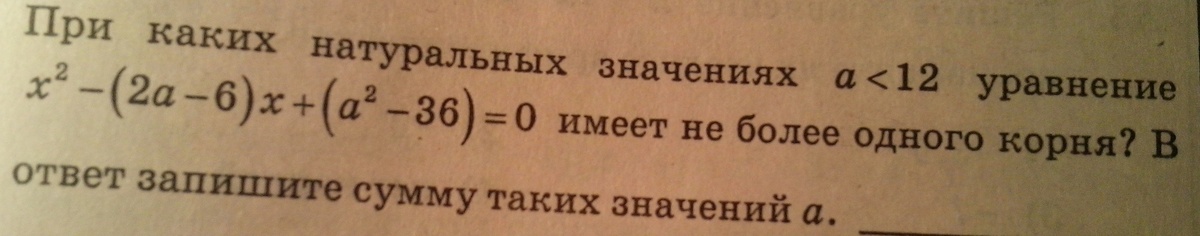
1) Уравнение x² — (2a — 4)x + (a² — 25) имеет 1 корень при D = 0.

D = b² — 4ac D = ( — (2a — 4))² — 4 * 1 * (a² — 25) = 4a² — 16a + 16 — 4a² + 100 — 16a + 116 = 0 a = 116 / 16 = 29 / 4.

Чтобы было 2 корня, D должно быть больше 0, т.

Е. а&lt ; 29 / 4, таких значений бесконечное множество.

2) Уравнение x² — (2a — 6)x + (a² — 36) имеет не более 1, т.

Е. 1 корень при D = 0, а менее , т.

Е. ни одного при D &lt ; 0.

D = b² — 4ac D = ( — (2a — 6))² — 4 * 1 * (a² — 36) = 4a² — 24a + 36 — 4a² + 144 — 24a + 180 = 0 a = 180 / 24 = 15 / 2 — один корень, при a &gt ; 15 / 2 — ни одного корня.

При каких значения параметра а уравнение имеет два различных натуральных корня : ах ^ 2 — (2а ^ 2 + 5)х + 10а = 0?

При каких значения параметра а уравнение имеет два различных натуральных корня : ах ^ 2 — (2а ^ 2 + 5)х + 10а = 0.

Не решая следующие уравнение укажите какие из них имеют действительные корни ; какие — не имеют действительных корней ; какие из уравнений с действительными корнями имеют равные корни Пожалуйста помог?

Не решая следующие уравнение укажите какие из них имеют действительные корни ; какие — не имеют действительных корней ; какие из уравнений с действительными корнями имеют равные корни Пожалуйста помогите даю 40 баллов 139 номер.

При каких натуральных значениях a корнем уравнения ax = 18 являются натуральное число ?

При каких натуральных значениях a корнем уравнения ax = 18 являются натуральное число ?

При каких значениях параметра корни уравнения имеют разные знаки и оба принадлежат отрезку [ — 2 ; 2] 4) При каких значениях парметра все решения неравенства принадлежат интервалу (0 ; 2)?

При каких значениях параметра корни уравнения имеют разные знаки и оба принадлежат отрезку [ — 2 ; 2] 4) При каких значениях парметра все решения неравенства принадлежат интервалу (0 ; 2).

При каких значениях (с) не имеет корней уравнение ?

При каких значениях (с) не имеет корней уравнение :

Найти натуральные значения с, при которых значение выражения 61 — с ^ 2всё под корнем является натуральным числом?

Найти натуральные значения с, при которых значение выражения 61 — с ^ 2всё под корнем является натуральным числом.

Приведите примеры линейных уравнений с действительными коэффициентами, которые : а) имеют целые корни, но не имеют натуральных корней ; б) имеют рациональные корни, но не имеют целых корней?

Приведите примеры линейных уравнений с действительными коэффициентами, которые : а) имеют целые корни, но не имеют натуральных корней ; б) имеют рациональные корни, но не имеют целых корней.

Приведите примеры линейных уравнений которые имеют 1 корень не имеют корней и имеют много корней?

Приведите примеры линейных уравнений которые имеют 1 корень не имеют корней и имеют много корней?

ПОЖАЛУЙСТААААА При каких натуральных значениях а уравнение х ^ 2 — (2а — 4)х + (а ^ 2 — 25) = 0 имеет не менее одного корня?

ПОЖАЛУЙСТААААА При каких натуральных значениях а уравнение х ^ 2 — (2а — 4)х + (а ^ 2 — 25) = 0 имеет не менее одного корня?

При каких значениях n уравнение не имеет корней?

При каких значениях n уравнение не имеет корней?

Вы находитесь на странице вопроса При каких натуральных значениях уравнения имеют более / менее одного корня? из категории Алгебра. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

5 задания б)y ^ 4 + y² — 6 = 0 y² = z z² + z — 6 = 0 D = 1² — 4·1· — 6 = 25 z₁ = 1 — 5 / 2 = — 2 z₂ = 1 + 5 / 2 = 3.

— 3 + 0, 4x, если х = 7, то — 3 + 0, 4 * 7 = — 0, 2 — 4 + 0, 5х, если х = 7, то — 4 + 0, 5 * 7 = — 0, 5 — 3 + 0, 4х> — 4 + 0, 5х — 0, 2> — 0, 5.

— 2x — 3x = 0 — 5x = 0 x = 0 Подставляем : 3 * 0 + 4 = 4.

1) (5a + 5c) + ( — ab — cb) = 5(a + c) — b(a + c) = (a + c)(5 — b) 2) — 3)a(a ^ 2 — 2ac + c ^ 2) = a(a — c) ^ 2 4) x ^ 3 + x ^ 2 + x + x ^ 2 + x + 1 — x ^ 3 + 9x = 2x ^ 2 + 1 + 11x.

2x ^ 2 + 3x — 5 = 0 D = 9 — 4 * 2 * ( — 5) = 9 + 40 = 49 = 7 ^ 2 x1 = ( — 3 + 7) / 4 = 1 x2 = ( — 3 — 7) / 4 = — 2, 75.

18) f ‘(x) = ( — 2)’ * ctgx — ( — 2) * (ctgx)’ = 0 * ctgx + 2 * ( — 1 / Sin²x) = — 2 / Sin²x 19) f ‘ (x) = (Sin15x)’ = Cos15x * (15x)’ = 15Cos15x 20) f ‘(x) = [Cos(π / 4 — 12x)] ‘ = — Sin(π / 4 — 12x) * (π / 4 — 12x)’ = 12Sin(π / 4 — 12x).

Корень — обратный процесс степени квадрат. Следовательно, корень 16 = 4 . Т. к. 4×4 = 16.

Корень из 16 = 4 как — то так.

Решение смотри на фотографии.

— 1. 2x + 0. 4 + 6. 4x — 2. 4 — 5 + 3. 8x + 4 = 0 9x — 3 = 0 x = 1 / 3.

Уравнения с параметром

Разделы: Математика

Справочный материал

Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.

Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет

Если 1 – а 0, т.е. а 1, то х =

Пример 4.

Если а = 1, то 0х = 0
х – любое действительное число

Если а = -1, то 0х = -2
Корней нет

Если а 1, а -1, то х = (единственное решение).

Это значит, что каждому допустимому значению а соответствует единственное значение х.

если а = 5, то х = = ;

Дидактический материал

3. а = +

4. + 3(х+1)

5. = –

6. =

Ответы:

1. При а1 х =;

1. При а3 х = ;

1. При а1, а-1, а0 х = ;

при а = 1 х – любое действительное число, кроме х = 1

1. При а2, а0 х = ;

1. При а-3, а-2, а0, 5 х =

1. При а + с0, с0 х = ;

Квадратные уравнения с параметром

Пример 1. Решить уравнение

х = –

В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.

Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16

a =

a =

Если а -4/5 и а 1, то Д > 0,

х =

х = – = –

Пример 2. При каких значениях параметра а уравнение

х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?

В итоге

4(а – 1)(а – 6) > 0 — 2(а + 1) 0

а 6 а > — 1 а > 5/9

6

Пример 3. Найдите значения а, при которых данное уравнение имеет решение.

Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а

4а 2 – 16 0

4а(а – 4) 0

а(а – 4)) 0

Ответ: а 0 и а 4

Дидактический материал

1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?

2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?

3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?

4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?

5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?

Показательные уравнения с параметром

Пример 1.Найти все значения а, при которых уравнение

9 х – (а + 2)*3 х-1/х +2а*3 -2/х = 0 (1) имеет ровно два корня.

Решение. Умножив обе части уравнения (1) на 3 2/х , получим равносильное уравнение

3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)

Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или

Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log₃2 , или х 2 – хlog₃2 + 1 = 0.

Это уравнение не имеет действительных корней, так как его Д = log 2 ₃2 – 4 х+1/х = а то х + 1/х = log₃а, или х 2 – хlog₃а + 1 = 0. (3)

Уравнение (3) имеет ровно два корня тогда и только тогда, когда

Д = log 2 ₃2 – 4 > 0, или |log₃а| > 2.

Если log₃а > 2, то а > 9, а если log₃а 9.

Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?

Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х₁ = -3, х₂ = а = >

а – положительное число.

Дидактический материал

1. Найти все значения а, при которых уравнение

25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.

2. При каких значениях а уравнение

2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?

3. При каких значениях параметра а уравнение

4 х — (5а-3)2 х +4а 2 – 3а = 0 имеет единственное решение?

Ответ:

1. 0 25/2
2. при а = 1, а = -2,2
3. 0 0, х1/4 (3)

х = у

Если а = 0, то –

2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4

Не выполняется (2) условие из (3).

Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.

Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).

Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х

Выражая х из (1) и подставляя в (2), получаем неравенство

2 – а > 1 – а (3)

Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.

Решения неравенства (3) образуют промежуток (а₀; 2), где а₀ 2

а₀ =

Ответ: x + 9a 3 ) = x имеет ровно два корня.

Найдите, при каких значениях а уравнение log ₂ (4 x – a) = x имеет единственный корень.

При каких значениях а уравнение х – log ₃ (2а – 9 х ) = 0 не имеет корней.

Ответы:

при а 16.06.2009