При каких значения уравнение имеет три корня

№ 31.13 ГДЗ Алгебра 10-11 класс Мордкович. При каких значениях а уравнение имеет три корня?

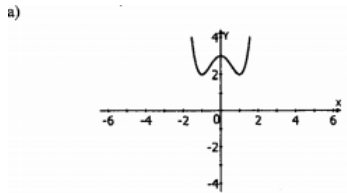
а) Постройте график функции у = х 4 — 2х 2 + 3.

б) При каких значениях параметра а уравнение х 4 — 2х 2 + 3 = а имеет три корня?

б) Количество корней в данном уравнении – это количество пересечений графиков у = х 4 – 2х 2 + 3 и у = а
Из рисунка видно, что такой случай имеет место, когда прямая у = а касается графика функции в точке (0; у(0)) у(0) = 3, следовательно, а = 3

Один из методов решения уравнений с параметром

Разделы: Математика

Уравнениями с параметром называются уравнения, у которых коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами.

Решить уравнение с параметром – это значит:

а) исследовать, при каких значениях параметров уравнение имеет корни и при каких не имеет;

б) выяснить количество корней при различных значениях параметров;

в) найти все выражения для корней.

Уравнения с параметром весьма различны по структуре:

Моя работа посвящена отысканию метода решения уравнений с параметрами вида

В основе этого метода лежит взгляд на параметр, как на переменную, т.е. уравнение F(x n ;p?)=0 можно рассматривать как квадратное относительно параметра р.

Задача 1. Пусть нужно решить уравнение с параметром

Преобразуем данное уравнение

Это уравнение 4-й степени относительно х, причём содержит и . Как его решить? Но заметим, что это уравнение является квадратным относительно , т.е. вида . Применим наш метод:

1. Перепишем уравнение в виде

, т.е. рассмотрим его как квадратное относительно .

2. Найдем корни уравнения по формуле корней квадратного уравнения:

3. Далее используем графический метод. В системе координат построим параболы , и ,

4. Найдём точки пересечения графиков функций. Для этого приравняем

, отсюда , т.е. точка пересечения единственная .

5. По рисунку видно, что горизонтальная прямая не имеет общих точек с параболами, если она проходит ниже , т.е.

при данное уравнение не имеет корней

при уравнение имеет единственный корень

при уравнение имеет два корня т.к. прямая имеет две точки пересечения с параболой , отсюда , ,

при и — три корня

при

при

при и уравнение имеет четыре корня

Этот метод не является универсальным, но во многих случаях является весьма результативным и позволяет решать уравнения повышенной сложности, второй степени и выше.

Задача 2. Определить число корней уравнения в зависимости от параметра а х 4 -10х 3 -2(а-11)х 2 +2(5а + 6)х +2а + а 2 =0 (1)

Решение. Уравнение является квадратным относительно параметра а. Перепишем (1) в виде (2)

Решая уравнение (2), находим

Построим в системе координат (х; а) графики функций

и (рис 2)

Найдем точки пересечения графиков функций. Для этого приравняем отсюда . Далее рассуждая аналогично, как и в задаче 1, получим

Ответ: если , уравнение корней не имеет;

если один корень;

если , уравнение имеет два корня;

если три корня;

если — четыре корня.

Задача 3. Найти все значения параметра р, при которых уравнение (3)

имеет ровно три решения.

Решении. Уравнение (3) является квадратным относительно р. Перепишем его в виде

Найдем корни уравнения

В системе координат (х; р) построим параболы

и (рис.2)

Данное уравнение имеет три решения при тех значениях параметра р, при которых горизонтальная прямая имеет три точки пересечения с параболами. Таким образом, уравнение (3) имеет три решения в следующих случаях:

1) прямая проходит через вершину одной параболы и пересекает другую в двух точках. Это возможно, когда т.е. при уравнение имеет три решения;

2) прямая проходит через точку пересечения парабол. Найдём абсциссу точки пересечения парабол, для этого решим уравнение

Если то т.е. при прямая пересекает параболы в трех точках, значит, исходное уравнение имеет три корня.

Ответ:

Задача 4. При каких значениях параметра а существует единственная пара (х; у), удовлетворяющая уравнению

(4)

Решение: Уравнение – квадратное относительно х.

(5)

1. Контрольным значением параметра является число , при котором уравнение (5) примет вид отсюда . Видно, что в этом случае решениями уравнения будут все пары , т.е. при исходное уравнение имеет бесконечное множество решений.

2. Пусть . Дискриминант уравнения (5)

Если т.е. , то , исходное уравнение имеет решение только тогда, когда , а — единственное решение.

Если же , исходное уравнение относительно х имеет решение при любом у.

Ответ: .

Задача 5. Решите уравнение

(6)

Решение. Уравнение является квадратным относительно р. Перепишем уравнение (6) в виде

(7)

Дискриминант квадратного уравнения (7)

Решая (7), получим

Здесь возможны случаи.

1. Уравнение (6) имеет четыре корня, если

Решая систему, получаем . Таким образом, при уравнение (6) имеет четыре корня ,

2. Уравнение (6) имеет три корня, если

Решая систему, получим Значит, при уравнение (6) имеет три корня

3. Уравнение (6) имеет два корня, если

Решая систему, получим , значит, при этих значениях параметра р уравнение (6) имеет два корня

4. Уравнение (6) имеет один корень, если

Решая систему, получим . Следовательно, при решением уравнения (6) будет .

5. Уравнение (5) не имеет корней, если

Ответ: если — корней нет;

если

если ;

если

если

Этот метод не является универсальным, но во многих случаях является весьма результативным и позволяет решать уравнения повышенной сложности. Иногда трудно предвидеть будет ли применение этого метода результативным, но такие уравнения существуют и поэтому его надо знать.

Например, с помощью этого метода можно решить следующие уравнения:

из сборника для подготовки к ЕГЭ.

из сборника Сканави

Задача 18 ЕГЭ-2021 по математике. Параметры

Посмотрите на условия задач с параметрами ЕГЭ-2021. Вы заметите, что на вид все они похожи. Однако сходство только внешнее, и решаются они по-разному. В этой статье – обзор задач с параметрами ЕГЭ-2021 по математике.

1. Начнем с задачи, которую лучше всего решить аналитическим способом. Слева в уравнении модуль, справа – произведение модуля и корня квадратного. Лучше всего первым действием сделать возведение обеих частей уравнения в квадрат (при неотрицательности подкоренного выражения).

О том, как решать уравнения, где слева модуль и справа модуль, читайте здесь: Уравнения с модулем.

При каких значениях параметра a уравнение

имеет ровно 2 решения?

Уравнение равносильно системе:

Вынесли общий множитель за скобку

Так как и при всех исходное уравнение имеет корни и при всех Значит, исходное уравнение имеет ровно два корня в следующих случаях:

не имеет решений и

2) совпадение корней

Рассмотрим первый случай.

Неравенство — не имеет решений, если

Рассмотрим второй случай.

1) Корни и совпадают, тогда и

Так как исходное уравнение при имеет один корень

2) Корни и совпадают.

Уравнение имеет корни и

3) Корни и совпадают, исходное уравнение имеет ровно два корня.

Мы применили аналитический способ решения: с помощью равносильных переходов от исходного уравнения перешли к такой форме, где сразу видно, какие корни имеет уравнение при определенных значениях параметра.

На Онлайн-курсе подготовки к ЕГЭ на 100 баллов мы подробно рассказывали об этом методе и решали множество задач. Способ хорош тем, что вы просто действуете по образцу – и быстро приходите к ответу.

2. Второе уравнение очень похоже на первое. И первое действие будет таким же: возведением обеих частей в квадрат. А закончим мы – для разнообразия – построением графиков в системе координат (а; х).

Найти a, при которых имеет ровно 2 решения.

Возведем обе части уравнения в квадрат.

Найдем, каким значениям параметра соответствует ровно два значения

Построим в системе координат графики функций:

Мы находим такие при которых горизонтальная прямая имеет ровно 2 общие точки с совокупностью прямых, являющихся графиком исходного уравнения.

Видим, что в общем случае прямая пересекает каждую из трех прямых, то есть исходное уравнение имеет ровно 3 решения.
Ровно 2 решения будет в случаях, когда прямая проходит через точки пересечения прямых, то есть в случаях совпадения корней.

Данная совокупность имеет ровно два решения в случаях совпадения корней.

О графическом способе решения задач с параметрами читайте здесь: Графический метод решения задач с параметрами.

3. В третьем задании также присутствуют выражения под модулями. Но подход будет другой: мы применим метод интервалов для модулей, о котором можно прочитать здесь: Уравнения с модулем.

С его помощью раскроем модули и получим график функции, заданной описанием: на разных интервалах график этой функции выглядит по-разному, то есть состоит из отдельных кусочков. А дальше – графическое решение.

Найдите все значения a, при каждом из которых уравнение

имеет ровно два различных корня.

Применим метод интервалов для модулей. Уравнение равносильно совокупности систем:

Мы сделали так, потому что при оба модуля раскрываем с противоположным знаком:

Заметим, что если уравнение не выполняется ни при каких

Решим графически полученную совокупность.

Рассмотрим функцию такую, что:

Для функции ось ординат – вертикальная асимптота.

Уравнение имеет ровно два корня при или

Вообще задачи с параметрами, как правило, можно решать многими способами.

4. И наконец, довольно сложное уравнение с тремя модулями. Нам придется раскрывать все эти модули по определению, рассматривая 4 случая. Но ничего страшного здесь нет – просто аккуратность. А потом мы разобьем координатную плоскость (х; а) на области и в каждой из областей построим график уравнения. Кто знаком с методом областей – тот легко с этим справится.

При каких значениях параметра a уравнение имеет ровно три различных решения