При каких значениях а корнем уравнения х(6 — а) + а(х + 2) = 26 является число 4?
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,298
- гуманитарные 33,622
- юридические 17,900
- школьный раздел 607,232
- разное 16,830
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
При каких значениях а корни уравнения
В.П.Василенков, Р.С. Златин, А.В. Дюндин
Раздел 1 . Уравнения
� 1.4. Уравнения с параметрами .
6. Квадратный трехчлен и параметры
Квадратный трехчлен в школе можно назвать главной функцией всей математики 8-9 классов, а также всей школьной математики.
Особую роль среди уравнений с параметрами играют задачи, связанные с расположением корней квадратного трехчлена. Для решения таких задач можно сформулировать теоремы, но, однако, количество таких теорем будет практически необозримо. И остается только одно- научиться придумывать теорему каждый раз, в каждой конкретной задаче. Для придумывания таких теорем нужно не только знание свойств квадратного трехчлена, но и умение мыслить одновременно на двух языках — алгебраическом и геометрическом.
Это значит, что для любого свойства, сформулированного на алгебраическом языке, нужно уметь дать геометрическую интерпретацию на графике, и наоборот. Например:
� старший коэффициент меньше нуля — значит ветви параболы направлены вниз;
� график функции у = ах 2 + bх + с находится выше оси абсцисс- значит а>0, b 2 — 4ac
Рассмотрим ряд примеров.
Пример 1. При каких значениях параметра а корни квадратного уравнения х 2 + (а + 1)х + 3 = 0 лежат по разные стороны от числа 2?
Построим график квадратного трехчлена, удовлетворяющий данному условию. Если потребовать, чтобы f(2) 2 + (a + 1)x + 3, то отсюда будет следовать, что корни уравнения существуют и лежат по разные стороны от числа 2. Верно и обратное, то есть справедлива следующая теорема.
Теорема. Для того, чтобы корни квадратного уравнения х 2 + рх + q = 0 лежали по разные стороны от числа к необходимо и достаточно, чтобы f(k)
В нашем случае f(2) = 4 + 2(а + 1) + 3 = 2а + 9, 2а + 9 Ответ: а
Пример 2. Найти все а, при которых корни уравнения х 2 + х + а = 0 различные и оба больше а.
Дадим геометрическую интерпретацию поставленной задачи (рис.9). Очевидно, что если f(a) > 0, хв > a и D > 0, то оба корня действительно различны и оба больше а. Ни одно из условий не является лишним.
Например, если отбросить условие D > 0, то возможна ситуация (см. рис. 10) и корней вообще нет, хотя f(a) > 0, xв > а.
Если отбросить условие f(a) > 0, то возможна ситуация (см. рис.11) и один корень меньше а, другой больше a , хотя D > 0 и хв > а.
Если отбросить условие хв > а, то возможна ситуация (см. рис. 12) и корни уравнения меньше а, хотя D > 0 и f(a) > 0.
Теорема. Для того, чтобы корни уравнения х 2 + рх + q = 0 были различны и оба больше к необходимо и достаточно, чтобы выполнялись условия:
В нашем примере f(a) = а 2 + а + а = а 2 + 2а, D = 1 — 4а, хв = — 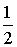
Получаем систему неравенств.
Систему решаем методом интервалов (рис. 13).
Ответ: а 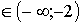
Пример 3. Найти все значения параметра р, при которых корни уравнения х 2 + (р + 1)х + р = 0 принадлежат промежутку (-2;3).
Дадим геометрическую интерпретацию этой задачи (см. рис.14).Очевидно, что если f(-2) > 0, f(3) > 0, D 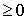
Итак, в нашем случае f(-2) = 4 — 2(p + 1) + p = 2 — p,
f(3) = 9 + 3(p + 1) + p = 12 + 4p,
D = (p + 1) 2 — 4p = (p — 1) 2 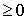
Итак, имеем систему неравенств:
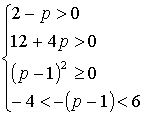
Пример 4. При каких а уравнение (1 + 2а)х 4 — 2ах 2 + (1 + а) = 0:
1) не имеет действительных корней;
2) имеет один корень;
3) имеет два корня;
4) имеет три корня;
5) имеет четыре корня.
Введем новую переменную у = х 2 . Тогда заданное уравнение равносильно уравнению (1 + 2а)у 2 — 2ау + (1 + а) = 0, где у = х 2 .
Изложим схему исследования.
1. Уравнение (1 + 2а)у 2 — 2ау + (1 + а) = 0 , где у = х 2 не имеет решений в трех случаях:
1) D = (2а) 2 — 4(1 + а)(1 + 2а)
2) D 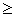
3) а = — 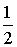
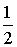
2. Система имеет один корень:
3. Система имеет два корня в случаях:
2)D > 0, у1 0 (корни находятся по разные стороны от нуля.)
4. Система имеет три корня, если D > 0, у1 > 0, у2 = 0.
5. Система имеет четыре корня, если D > 0, у1 > 0, у2 > 0 (оба корня правее нуля.)
Дальнейшее исследование проводится аналогично предыдущим случаям. Получите решение самостоятельно!
7. Теорема Виета и параметры.
Многие уравнения с параметрами связаны с использованием теоремы Виета. При этом важно понимать, что теорема Виета в школьном курсе формулируется только для случая, когда существуют действительные корни уравнения, в противном случае можем получить ошибочный ответ (см. пункт 4 примеров 1 и 2).
Приведем некоторые примеры, в которых используется теорема Виета.
Пример 1. При каких а разность корней уравнения 2х 2 — (а + 1)х + (а — 1) =0 равна их произведению?
Прежде всего заметим, что теорема Виета применима при любом а, так как
D = (а + 1) 2 — 8(а — 1) = а 2 — 6а + 9 = (а — 3) 2 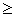
По теореме Виета 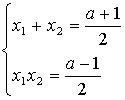
тогда 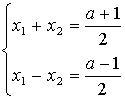
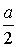
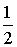
Тогда 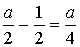
Пример 2. Найти наименьшее значение выражения х1 2 + х2 2 , если х1 и х2 � корни уравнения х 2 — 2ах + а + 6 = 0.
По теореме Виета х1+ х2 = 2а,
Казалось бы, мы должны найти наименьшее значение выражения 4а 2 — 2а — 12, а оно достигается в вершине параболы у = 4а 2 — 2а — 12,
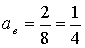
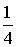
На самом деле мы опять допускаем ту же ошибку, т. е. если подставить 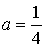
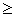
Решая неравенство, получим 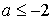
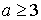
Из графика функции у = 4а 2 — 2а — 12 (см. рис. 16) видно, что наименьшее значение будет среди двух чисел f (-2) и f (3):
Итак, наименьшее значение выражения х1 + х2 равно 8 при а = -2.
Упражнения
4.1. 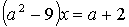
4.2. 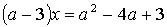
4.3. 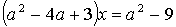
4.4. 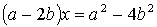
4.5. 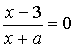
4.6. 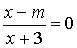
4.7. 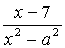
4.8. 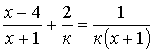
4.9. 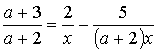
4.10. 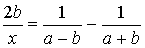
4.11. 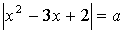
4.12. 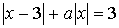
4.13. 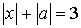
4.14. Найти все значения параметра а, для которых квадратное уравнение 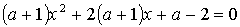
а) имеет два корня;
б) имеет один корень;
в) не имеет корней.
4.15. 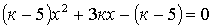
4.16. 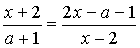
4.17. 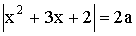
4.18. 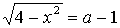
4.19. 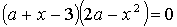
4.20. При каких а уравнение 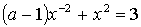
4.21. При каких а интервал (2;3) находится между корней уравнения 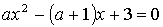
Указание. Рассмотреть два случая: 1) a >0; 2) a
4.22. При каких m уравнение 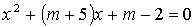
4.23. При каких к корни уравнения 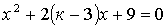
4.24. Найти все р, при которых один корень уравнения 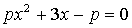
4.25. Вычислить сумму корней уравнения 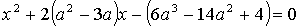
Указание : х1 + х2 = 6а — 2а 2 . Требуется найти наибольшее значение 6а — 2а 2 при условии, что D 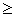
4.26. Решить уравнение 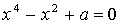
4.27. При каких а уравнение 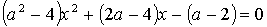
1) имеет не более одного решения;
2) не менее одного решения.
Обязательно самостоятельно выполните
1.1(а,в); 1.2(а); 1.3(а); 2.4; 2.13; 3.1; 3.5; 4.2; 4.6; 4.9.
1.2(б); 1.4; 2.12; 2.15; 3.10; 4.14; 4.16; 4.21; 4.23; 4.25.
Уравнения с параметром
Разделы: Математика
Справочный материал
Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.
Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.
Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет
Если 1 – а 

Пример 4.
Если а = 1, то 0х = 0
х – любое действительное число
Если а = -1, то 0х = -2
Корней нет
Если а 


Это значит, что каждому допустимому значению а соответствует единственное значение х.
если а = 5, то х =
=
;
Дидактический материал
3. а = 
4. 
5. 

6. 
Ответы:
- При а
1 х =
;
- При а
3 х =
;
- При а
1, а
-1, а
0 х =
;
при а = 1 х – любое действительное число, кроме х = 1
- При а
2, а
0 х =
;
- При а
-3, а
-2, а
0, 5 х =
- При а + с
0, с
0 х =
;
Квадратные уравнения с параметром
Пример 1. Решить уравнение
х = –
В случае а 
Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16
a =
a =
Если а -4/5 и а 
х =
х = – 
Пример 2. При каких значениях параметра а уравнение
х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?
| В итоге |  | 4(а – 1)(а – 6) > 0 — 2(а + 1) 0 |  | а 6 а > — 1 а > 5/9 | |
Пример 3. Найдите значения а, при которых данное уравнение имеет решение.
Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а
4а 2 – 16 
4а(а – 4) 
а(а – 4)) 
Ответ: а 

Дидактический материал
1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?
2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?
3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?
4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?
5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?
Показательные уравнения с параметром
Пример 1.Найти все значения а, при которых уравнение
9 х – (а + 2)*3 х-1/х +2а*3 -2/х = 0 (1) имеет ровно два корня.
Решение. Умножив обе части уравнения (1) на 3 2/х , получим равносильное уравнение
3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)
Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или
Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log32 , или х 2 – хlog32 + 1 = 0.
Это уравнение не имеет действительных корней, так как его Д = log 2 32 – 4 х+1/х = а то х + 1/х = log3а, или х 2 – хlog3а + 1 = 0. (3)
Уравнение (3) имеет ровно два корня тогда и только тогда, когда
Д = log 2 32 – 4 > 0, или |log3а| > 2.
Если log3а > 2, то а > 9, а если log3а 9.
Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?
Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х1 = -3, х2 = а = >
а – положительное число.
Дидактический материал
1. Найти все значения а, при которых уравнение
25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.
2. При каких значениях а уравнение
2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?
3. При каких значениях параметра а уравнение
4 х — (5а-3)2 х +4а 2 – 3а = 0 имеет единственное решение?
Ответ:
- 0 25/2
- при а = 1, а = -2,2
- 0 0, х
1/4 (3)

| Если а = 0, то – | 2у + 1 = 0 2у = 1 у = 1/2  х = 1/2 х = 1/2 х = 1/4 |
Не выполняется (2) условие из (3).
Пусть а 


Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).
Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х
Выражая х из (1) и подставляя в (2), получаем неравенство

Чтобы решить неравенство (3), построим графики функций у = 
Решения неравенства (3) образуют промежуток (а0; 2), где а0 2
а0 =
Ответ: 
Ответы:
- при а 16.06.2009
http://sgpu-fmf.narod.ru/FMSh/2/1_4_4.htm
http://urok.1sept.ru/articles/534897
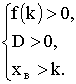
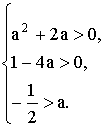
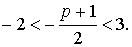
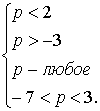

 =
=  ;
;


 ;
; ;
; ;
; ;
;
 ;
;




 6
6