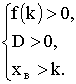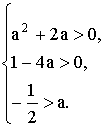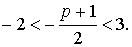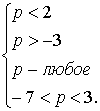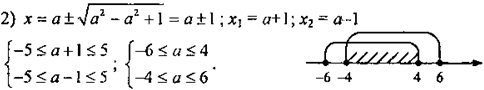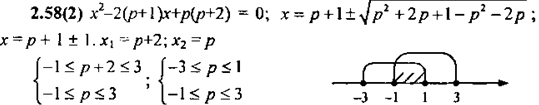При каких значениях а корни уравнения принадлежат промежутку

При каких значениях а корни уравнения принадлежат промежутку

В.П.Василенков, Р.С. Златин, А.В. Дюндин

Раздел 1 . Уравнения

� 1.4. Уравнения с параметрами .

6. Квадратный трехчлен и параметры

Квадратный трехчлен в школе можно назвать главной функцией всей математики 8-9 классов, а также всей школьной математики.

Особую роль среди уравнений с параметрами играют задачи, связанные с расположением корней квадратного трехчлена. Для решения таких задач можно сформулировать теоремы, но, однако, количество таких теорем будет практически необозримо. И остается только одно- научиться придумывать теорему каждый раз, в каждой конкретной задаче. Для придумывания таких теорем нужно не только знание свойств квадратного трехчлена, но и умение мыслить одновременно на двух языках — алгебраическом и геометрическом.

Это значит, что для любого свойства, сформулированного на алгебраическом языке, нужно уметь дать геометрическую интерпретацию на графике, и наоборот. Например:

� старший коэффициент меньше нуля — значит ветви параболы направлены вниз;

� график функции у = ах 2 + bх + с находится выше оси абсцисс- значит а>0, b 2 — 4ac

Рассмотрим ряд примеров.

Пример 1. При каких значениях параметра а корни квадратного уравнения х 2 + (а + 1)х + 3 = 0 лежат по разные стороны от числа 2?

Построим график квадратного трехчлена, удовлетворяющий данному условию. Если потребовать, чтобы f(2) 2 + (a + 1)x + 3, то отсюда будет следовать, что корни уравнения существуют и лежат по разные стороны от числа 2. Верно и обратное, то есть справедлива следующая теорема.

Теорема. Для того, чтобы корни квадратного уравнения х 2 + рх + q = 0 лежали по разные стороны от числа к необходимо и достаточно, чтобы f(k)

В нашем случае f(2) = 4 + 2(а + 1) + 3 = 2а + 9, 2а + 9 Ответ: а

Пример 2. Найти все а, при которых корни уравнения х 2 + х + а = 0 различные и оба больше а.

Дадим геометрическую интерпретацию поставленной задачи (рис.9). Очевидно, что если f(a) > 0, х_в > a и D > 0, то оба корня действительно различны и оба больше а. Ни одно из условий не является лишним.

Например, если отбросить условие D > 0, то возможна ситуация (см. рис. 10) и корней вообще нет, хотя f(a) > 0, x_в > а.

Если отбросить условие f(a) > 0, то возможна ситуация (см. рис.11) и один корень меньше а, другой больше a , хотя D > 0 и х_в > а.

Если отбросить условие х_в > а, то возможна ситуация (см. рис. 12) и корни уравнения меньше а, хотя D > 0 и f(a) > 0.

Теорема. Для того, чтобы корни уравнения х 2 + рх + q = 0 были различны и оба больше к необходимо и достаточно, чтобы выполнялись условия:

В нашем примере f(a) = а 2 + а + а = а 2 + 2а, D = 1 — 4а, х_в = — .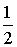

Получаем систему неравенств.

Систему решаем методом интервалов (рис. 13).

Ответ: а .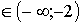

Пример 3. Найти все значения параметра р, при которых корни уравнения х 2 + (р + 1)х + р = 0 принадлежат промежутку (-2;3).

Дадим геометрическую интерпретацию этой задачи (см. рис.14).Очевидно, что если f(-2) > 0, f(3) > 0, D 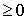, -2

Итак, в нашем случае f(-2) = 4 — 2(p + 1) + p = 2 — p,

f(3) = 9 + 3(p + 1) + p = 12 + 4p,

D = (p + 1) 2 — 4p = (p — 1) 2 ,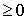

Итак, имеем систему неравенств:

или

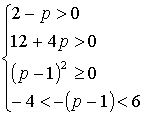
Пример 4. При каких а уравнение (1 + 2а)х 4 — 2ах 2 + (1 + а) = 0:

1) не имеет действительных корней;

2) имеет один корень;

3) имеет два корня;

4) имеет три корня;

5) имеет четыре корня.

Введем новую переменную у = х 2 . Тогда заданное уравнение равносильно уравнению (1 + 2а)у 2 — 2ау + (1 + а) = 0, где у = х 2 .

Изложим схему исследования.

1. Уравнение (1 + 2а)у 2 — 2ау + (1 + а) = 0 , где у = х 2 не имеет решений в трех случаях:

1) D = (2а) 2 — 4(1 + а)(1 + 2а)

2) D 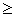0 и у₁

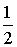
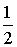
3) а = — (тогда у = — ).

2. Система имеет один корень:

3. Система имеет два корня в случаях:

2)D > 0, у₁ 0 (корни находятся по разные стороны от нуля.)

4. Система имеет три корня, если D > 0, у₁ > 0, у₂ = 0.

5. Система имеет четыре корня, если D > 0, у₁ > 0, у₂ > 0 (оба корня правее нуля.)

Дальнейшее исследование проводится аналогично предыдущим случаям. Получите решение самостоятельно!

7. Теорема Виета и параметры.

Многие уравнения с параметрами связаны с использованием теоремы Виета. При этом важно понимать, что теорема Виета в школьном курсе формулируется только для случая, когда существуют действительные корни уравнения, в противном случае можем получить ошибочный ответ (см. пункт 4 примеров 1 и 2).

Приведем некоторые примеры, в которых используется теорема Виета.

Пример 1. При каких а разность корней уравнения 2х 2 — (а + 1)х + (а — 1) =0 равна их произведению?

Прежде всего заметим, что теорема Виета применима при любом а, так как

D = (а + 1) 2 — 8(а — 1) = а 2 — 6а + 9 = (а — 3) 2 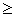0.

По теореме Виета 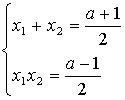и кроме того х₁-х₂ = х₁х₂,

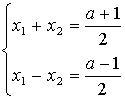
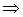
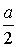
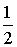
тогда х₁= , х₂= .

Тогда 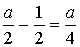, а = 2.

Пример 2. Найти наименьшее значение выражения х₁ 2 + х₂ 2 , если х₁ и х₂ � корни уравнения х 2 — 2ах + а + 6 = 0.

По теореме Виета х₁+ х₂ = 2а,

Казалось бы, мы должны найти наименьшее значение выражения 4а 2 — 2а — 12, а оно достигается в вершине параболы у = 4а 2 — 2а — 12,

, и а = .

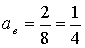
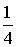
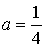
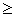
На самом деле мы опять допускаем ту же ошибку, т. е. если подставить в уравнение, то оно не имеет решений. Поэтому мы должны найти, при каких а теорема Виета применима, то есть D = 4а 2 — 4а — 24 0.

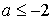
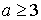
Решая неравенство, получим или .

Из графика функции у = 4а 2 — 2а — 12 (см. рис. 16) видно, что наименьшее значение будет среди двух чисел f (-2) и f (3):

Итак, наименьшее значение выражения х₁ + х₂ равно 8 при а = -2.

Упражнения

4.1. .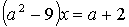

4.2. .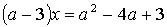

4.3. .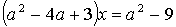

4.4. .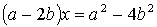

4.5. .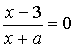

4.6. .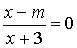

4.7. 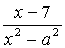=0.

4.8. .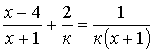

4.9. .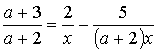

4.10. .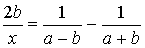

4.11. .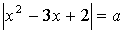

4.12. .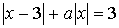

4.13. .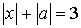

4.14. Найти все значения параметра а, для которых квадратное уравнение :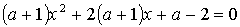

а) имеет два корня;

б) имеет один корень;

в) не имеет корней.

4.15. .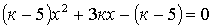

4.16. .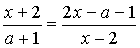

4.17. .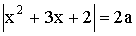

4.18. .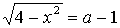

4.19. .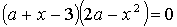

4.20. При каких а уравнение 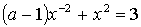имеет единственное решение?

4.21. При каких а интервал (2;3) находится между корней уравнения ?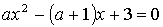

Указание. Рассмотреть два случая: 1) a >0; 2) a

4.22. При каких m уравнение 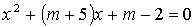имеет один корень больше 2, другой меньше 2?

4.23. При каких к корни уравнения 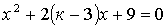принадлежат интервалу (-6;1)?

4.24. Найти все р, при которых один корень уравнения 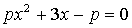больше 3, другой � меньше 2.

4.25. Вычислить сумму корней уравнения 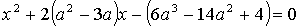и найти значение а, при котором соответствующая эта сумма принимает наибольшее значение.

Указание : х₁ + х₂ = 6а — 2а 2 . Требуется найти наибольшее значение 6а — 2а 2 при условии, что D 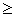0.

4.26. Решить уравнение .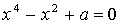

4.27. При каких а уравнение :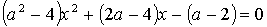

1) имеет не более одного решения;

2) не менее одного решения.

Обязательно самостоятельно выполните

1.1(а,в); 1.2(а); 1.3(а); 2.4; 2.13; 3.1; 3.5; 4.2; 4.6; 4.9.

1.2(б); 1.4; 2.12; 2.15; 3.10; 4.14; 4.16; 4.21; 4.23; 4.25.

Квадратные уравнения с параметром

Уравнение называется квадратным, если имеет вид \(ax^2+bx+c=0,\) где \(a,b,c\) — любые числа \((a≠0)\). При этом надо быть внимательным, если \(a=0\), то уравнение будет линейным, а не квадратным. Поэтому, первым делом при решении квадратного уравнения с параметром, рекомендую смотреть на коэффициент при \(x^2\) и рассматривать 2 случая: \(a=0\) (линейное уравнение); \(a≠0\) (квадратное уравнение). Квадратное уравнение часто решается при помощи дискриминанта или теоремы Виета.

Исследование квадратного многочлена

Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1) Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:

• Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа \(γ\): \(x_1≤x_2 0)\); ветки параболы направлены вниз \((a 0\). Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число \(γ\) должно по условию лежать вне отрезка \((x_1,x_2)\), то \(f(γ)>0\).
• \(a 0\). Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа \(γ\).

В итоге получаем:

если \(a*f(γ) 0\), то \(γ∉(x_1,x_2)\).

Нам осталось наложить условие, чтобы наши корни были слева от числа \(γ\). Здесь нужно просто сравнить положение вершины нашей параболы \(x_0\) относительно \(γ\). Заметим, что вершина лежит между точками \(x_1\) и \(x_2\). Если \(x_0 0, \\x_0

При каких значениях параметра a уравнение $$a(a+3) x^2+(2a+6)x-3a-9=0$$ имеет более одного корня?

1 случай: Если \(a(a+3)=0\), то уравнение будет линейным. При \(a=0\) исходное уравнение превращается в \(6x-9=0\), корень которого \(x=1,5\). Таким образом, при \(a=0\) уравнение имеет один корень.
При \(a=-3\) получаем \(0*x^2+0*x-0=0\), корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.

2 случай: Если \(a≠0; a≠-3\), то получим квадратное уравнение. При положительном дискриминанте уравнение будет иметь более одного корня: $$D>0$$ $$D/4=(a+3)^2+3a(a+3)^2>0$$ $$(a+3)^2 (3a+1)>0$$ $$a>-\frac<1><3>.$$ С учетом \(a≠0;\) \(a≠-3\), получим, что уравнение имеет два корня при \(a∈(-\frac<1><3>;0)∪(0;+∞)\). Объединив оба случая получим (внимательно прочитайте, что от нас требуется):

Найти все значения параметра a, при которых корни уравнения $$(a+1) x^2-(a^2+2a)x-a-1=0$$ принадлежат отрезку \([-2;2]\).

1 случай: Если \(a=-1\), то \(0*x^2-x+1-1=0\) отсюда \(x=0\). Это решение принадлежит \([-2;2]\).

2 случай: При \(a≠-1\), получаем квадратное уравнение, с условием, что все корни принадлежат \([-2;2]\). Для решения введем функцию \(f(x)=(a+1) x^2-(a^2+2a)x-a-1\) и запишем систему, которая задает требуемые условия:

Подставляем полученные выражения в систему:

Раздел II. № 2.58. ГДЗ Алгебра 9 класс ОГЭ Кузнецова. При каких значениях р корни уравнения принадлежат промежутку?

1) При каких значениях а корни уравнения
х 2 -2ах + (а + 1)(а — 1) = 0
принадлежат промежутку [-5; 5]?

2) При каких значениях р корни уравнения
х 2 -2(р + 1)х + р(р + 2) = 0
принадлежат промежутку [-1; 3]?

(1) х 2 -2ах+(а+1)(а-1) = 0
1) x 2 -2ах+a 2 -1 = 0

Ответ: при -4 ≤ а ≤ 4 .

Ответ: при -1 ≤ р ≤ 1.