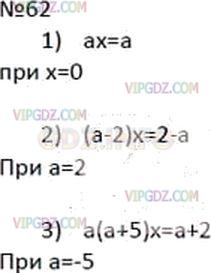При каком значении а корни уравнения

Решение на Упражнение 62 из ГДЗ по Алгебре за 7 класс: Мерзляк А.Г.

Условие

Решение 1

Решение 2

Поиск в решебнике

При каких значениях а корни уравнения х2-8ах+27=0 относятся как 3:1

Пусть один из корней равен k, тогда второй 3k.
По т. Виета х1*х2=27
k*3k=27
k^2=9
k=+-3
корни 3 и 9 или -3 и -9
По т. Виета х1+х2=8а
1) 3+9=8а; 8а=12; а=1,5;
2) -3+(-9)=8а; 8а=-12; а=-1,5.
Ответ: а=1,5 или а=-1,5.

.
D/4 = 16a^2 — 27 >=0 => a E (-bes; -3V3] U [3V3; bes)
x2 / x1 = (4a — sqr(D/4)) / (4a + sqr(D/4) = 3
Решаешь это уравнение и находишь, с учётом ОДЗ

D = (8a)^2 — 4*27 = 64a^2 — 108 = 4 (16a^2 — 27)
a^2 > 27/16
I a I > 3/4 * sqrt 3

x1 = [8a + 2 sqrt (16a^2-27) ] / 2 = 4a + sqrt (16a^2-27)

x2 = [8a — 2 sqrt (16a^2-27) ] / 2 = 4a — sqrt (16a^2-27)

4a + sqrt (16a^2-27) = 3 * [ 4a — sqrt (16a^2-27) ]

4a + sqrt (16a^2-27) = 12 a — 3 sqrt (16a^2-27)
4 sqrt (16a^2-27) = 8a
sqrt (16a^2-27) = 2a
a>0 (а при D>0 —a > 3/4 * sqrt 3)

возводим обе части в квадрат
16a^2-27 = 4a^2
12 a^2 — 27 = 0
a^2 = 27/12
a^2 = 2.25
I a I = 1.5
a1 = -1,5 не удовл. условию a > 0 (при возведении в квадрат)

Проверка:
x^2 — 8*1.5*x + 27 = 0
x^2 — 12x + 27 = 0
D = 144 — 108 = 36 = 6^2
x = (12 +/-6) / 2 = 6 +/-3
x1 = 6+3 = 9
x2 = 6-3 = 3
9/3 = 3 условие выполнено

Квадратные уравнения с параметром

Уравнение называется квадратным, если имеет вид $ax^2+bx+c=0,$ где $a,b,c$ — любые числа $(a≠0)$. При этом надо быть внимательным, если $a=0$, то уравнение будет линейным, а не квадратным. Поэтому, первым делом при решении квадратного уравнения с параметром, рекомендую смотреть на коэффициент при $x^2$ и рассматривать 2 случая: $a=0$ (линейное уравнение); $a≠0$ (квадратное уравнение). Квадратное уравнение часто решается при помощи дискриминанта или теоремы Виета.

Исследование квадратного многочлена

Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1) Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:

Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа $γ$: $x_1≤x_2 0)$; ветки параболы направлены вниз $(a 0$. Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число $γ$ должно по условию лежать вне отрезка $(x_1,x_2)$, то $f(γ)>0$.
$a 0$. Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа $γ$.

В итоге получаем:

если $a*f(γ) 0$, то $γ∉(x_1,x_2)$.

Нам осталось наложить условие, чтобы наши корни были слева от числа $γ$. Здесь нужно просто сравнить положение вершины нашей параболы $x_0$ относительно $γ$. Заметим, что вершина лежит между точками $x_1$ и $x_2$. Если \(x_0 0, \\x_0

При каких значениях параметра a уравнение $$a(a+3) x^2+(2a+6)x-3a-9=0$$ имеет более одного корня?

1 случай: Если $a(a+3)=0$, то уравнение будет линейным. При $a=0$ исходное уравнение превращается в $6x-9=0$, корень которого $x=1,5$. Таким образом, при $a=0$ уравнение имеет один корень.
При $a=-3$ получаем $0*x^2+0*x-0=0$, корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.

2 случай: Если $a≠0; a≠-3$, то получим квадратное уравнение. При положительном дискриминанте уравнение будет иметь более одного корня: $$D>0$$ $$D/4=(a+3)^2+3a(a+3)^2>0$$ $$(a+3)^2 (3a+1)>0$$ $$a>-\frac<1><3>.$$ С учетом $a≠0;$ $a≠-3$, получим, что уравнение имеет два корня при $a∈(-\frac<1><3>;0)∪(0;+∞)$. Объединив оба случая получим (внимательно прочитайте, что от нас требуется):

Найти все значения параметра a, при которых корни уравнения $$(a+1) x^2-(a^2+2a)x-a-1=0$$ принадлежат отрезку $[-2;2]$.

1 случай: Если $a=-1$, то $0*x^2-x+1-1=0$ отсюда $x=0$. Это решение принадлежит $[-2;2]$.

2 случай: При $a≠-1$, получаем квадратное уравнение, с условием, что все корни принадлежат $[-2;2]$. Для решения введем функцию $f(x)=(a+1) x^2-(a^2+2a)x-a-1$ и запишем систему, которая задает требуемые условия:

Подставляем полученные выражения в систему:

источники:

http://sprashivalka.com/tqa/q/23599674

http://sigma-center.ru/quadratic_equation_parametr