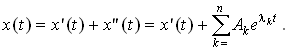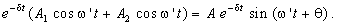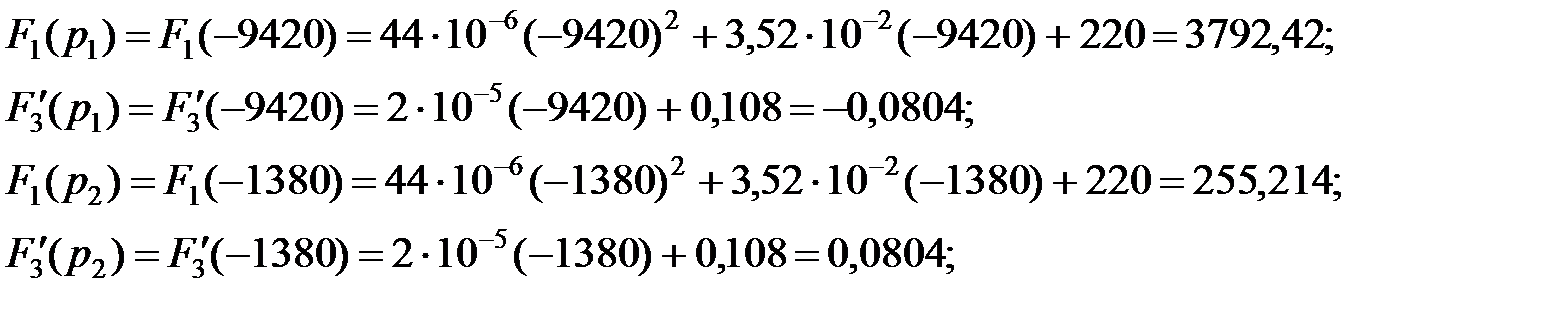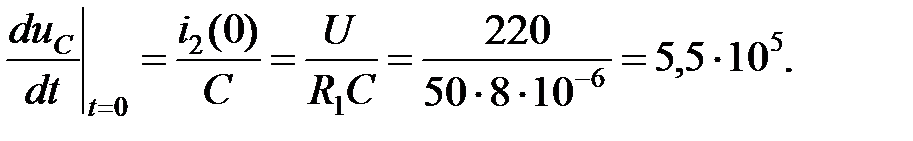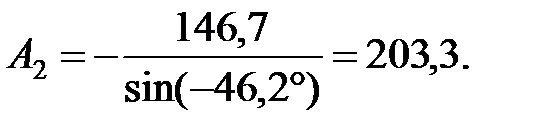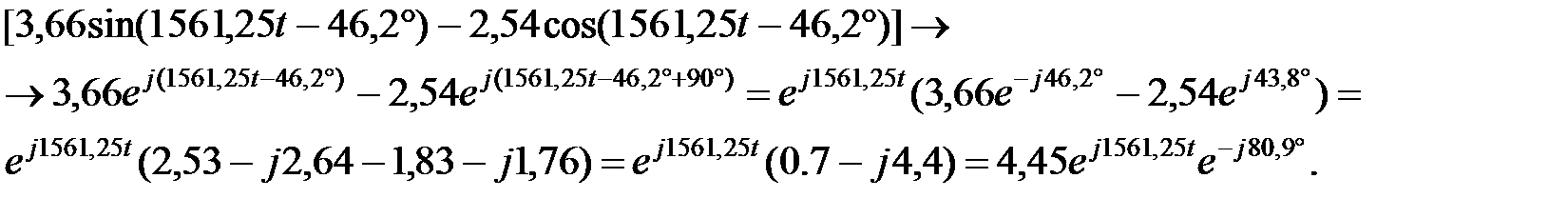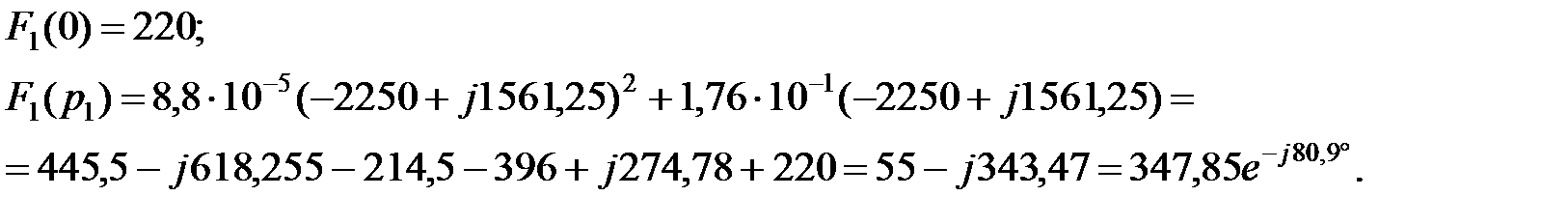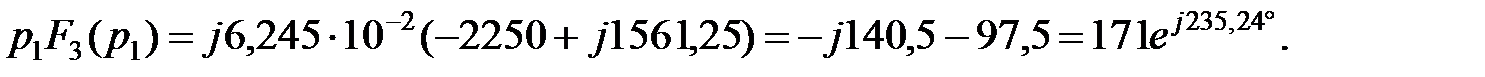При комплексных сопряженных корнях характеристического уравнения свободная составляющая

При комплексных сопряженных корнях характеристического уравнения свободная составляющая

При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.

При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.

Основные методы анализа переходных процессов в линейных цепях:

1. Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
2. Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
3. Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
4. Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
5. Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).

Классический метод расчета

Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.

В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.

Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи

;

при наличии магнитной связи с катушкой, обтекаемой током ,

;

Для последовательной цепи, содержащей линейные резистор R, катушку индуктивности L и конденсатор С, при ее подключении к источнику с напряжением u (см. рис. 1) можно записать

.

(1)

Подставив в (1) значение тока через конденсатор

,

получим линейное дифференциальное уравнение второго порядка относительно

.

В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:

,

(2)

где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); — известное возмущающее воздействие (напряжение и (или) ток источника электрической энергии); — к-й постоянный коэффициент, определяемый параметрами цепи.

Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.

В общем случае порядок дифференциального уравнения определяется соотношением

,

(3)

где и — соответственно число катушек индуктивности и конденсаторов после указанного упрощения исходной схемы; — число узлов, в которых сходятся только ветви, содержащие катушки индуктивности (в соответствии с первым законом Кирхгофа ток через любую катушку индуктивности в этом случае определяется токами через остальные катушки); — число контуров схемы, ветви которых содержат только конденсаторы (в соответствии со вторым законом Кирхгофа напряжение на любом из конденсаторов в этом случае определяется напряжениями на других).

Наличие индуктивных связей на порядок дифференциального уравнения не влияет.

Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение , соответствующее искомой переменной х в установившемся послекоммутационном режиме (теоретически для ).

Частное решение уравнения (2) определяется видом функции , стоящей в его правой части, и поэтому называется принужденной составляющей. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников принужденная составляющая определяется путем расчета стационарного режима работы схемы после коммутации любым из рассмотренных ранее методов расчета линейных электрических цепей.

Вторая составляющая общего решения х уравнения (2) – решение (2) с нулевой правой частью – соответствует режиму, когда внешние (принуждающие) силы (источники энергии) на цепь непосредственно не воздействуют. Влияние источников проявляется здесь через энергию, запасенную в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется свободным, а переменная — свободной составляющей.

В соответствии с вышесказанным, общее решение уравнения (2) имеет вид

(4)

Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.

Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.

Начальные условия. Законы коммутации

В соответствии с определением свободной составляющей в ее выражении имеют место постоянные интегрирования , число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий, которые принято делить на независимые и зависимые. К независимым начальным условиям относятся потокосцепление (ток) для катушки индуктивности и заряд (напряжение) на конденсаторе в момент времени (момент коммутации). Независимые начальные условия определяются на основании законов коммутации (см. табл. 2).

Таблица 2. Законы коммутации

Первый закон коммутации (закон сохранения потокосцепления)

Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .

Второй закон коммутации (закон сохранения заряда)

Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .

Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения и , что приводит к нарушению законов Кирхгофа.

На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:

первый закон коммутации – в ветви с катушкой индуктивности ток в момент

коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .

второй закон коммутации – напряжение на конденсаторе в момент

коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .

Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям (название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).

Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа . Аналогично при размыкании ключа в схеме на рис. 2,б трактование первого закона коммутации как невозможность скачкообразного изменения тока через катушку индуктивности приводит к невыполнению первого закона Кирхгофа . Для данных схем, исходя из сохранения заряда и соответственно потокосцепления, можно записать:

Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для . Необходимое число начальных условий равно числу постоянных интегрирования. Поскольку уравнение вида (2) рационально записывать для переменной, начальное значение которой относится к независимым начальным условиям, задача нахождения начальных условий обычно сводится к нахождению значений этой переменной и ее производных до (n-1) порядка включительно при .

Пример. Определить токи и производные и в момент коммутации в схеме на рис. 3, если до коммутации конденсатор был не заряжен.

В соответствии с законами коммутации

и .

На основании второго закона Кирхгофа для момента коммутации имеет место

,

и .

Для известных значений и из уравнения

определяется .

Значение производной от напряжения на конденсаторе в момент коммутации (см. табл. 1)

.

Корни характеристического уравнения. Постоянная времени

Выражение свободной составляющей общего решения х дифференциального уравнения (2) определяется видом корней характеристического уравнения (см. табл. 3).

Таблица 3. Выражения свободных составляющих общего решения

Вид корней характеристического уравнения

Выражение свободной составляющей

Корни вещественные и различные

Корни вещественные и

Пары комплексно-сопряженных корней

Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.

При вещественных корнях монотонно затухает, и имеет место апериодический переходный процесс. Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).

Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением

,

которое называется декрементом колебания, или натуральным логарифмом этого отношения

,

называемым логарифмическим декрементом колебания, где .

Важной характеристикой при исследовании переходных процессов является постоянная времени t , определяемая для цепей первого порядка, как:

,

где р – корень характеристического уравнения.

Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
3. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.

При комплексных сопряженных корнях характеристического уравнения свободная составляющая

17.3. О ХАРАКТЕРЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ

Из приведенных выше примеров следует, что токи и напряжения при переходном процессе в цепи n -го порядка, описываемой n уравнениями состояния, x ( t ) выражаются суммой вынужденной составляющей x’ ( t ), обусловленной источниками, и свободной составляющей x» ( t ), представляющей при отсутствии кратных корней сумму экспонент 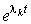, в показатели которых входят корни характеристического уравнения l k

Расположение корней l k на комплексной плоскости, обозначенных крестиками на рис. 17.1, а , определяет характер слагаемых свободной составляющей.

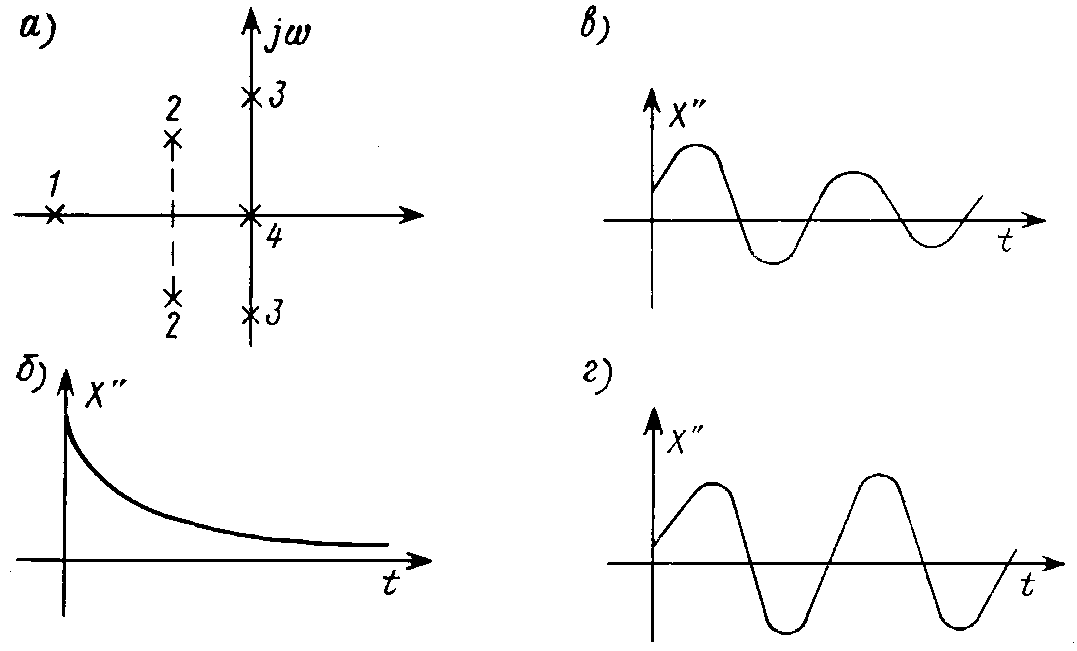
Простые вещественные корни l k = – a (точка 1 на рис. 17.1, а ) определяют экспоненциально затухающие апериодические слагаемые свободной составляющей A e – a t (рис. 17.1, б ). Комплексные сопряженные пары корней l k = – d ± j w ‘ (точки 2 на рис. 17.1, а ) дают экспоненциально затухающие колебательные составляющие (рис. 17.1, в )

Чисто мнимые пары корней (точки 3 на рис. 17.1, а ) обусловливают незатухающие синусоидальные колебания A sin ( w t + q ) (рис. 17.1, г ).

Свободный процесс в пассивной цепи с потерями носит затухающий характер, что связано с рассеянием энергии в резистивных элементах цепи. Поэтому для таких цепей имеем лишь вещественные отрицательные и комплексно сопряженные корни с отрицательной вещественной частью (точки 1 и 2 на рис. 17.1, а ). Сопряженный характер корней определяется тем, что характеристическое уравнение имеет вещественные коэффициенты. Так как колебательный характер свободных составляющих x «( t ) связан с периодическим обменом энергией между катушками и конденсаторами цепи, то комплексно сопряженные корни описывают процессы в пассивных цепях с RLC -элементами. При приближении пары комплексно сопряженных корней к мнимой оси интенсивность затухания колебательного процесса, выражаемая декрементом D , уменьшается. Как будет показано в Лекции 22, пассивные цепи с элементами RC и RL описываются лишь простыми вещественными корнями. LC -цепи также характеризуются простыми чисто мнимыми корнями. Кратные корни могут встретиться при описании процессов в пассивных RLC -цепях.

Если пассивная цепь с исключенными источниками, отвечающая свободным составляющим переходного процесса, имеет емкостные сечения (простейший случай — последовательно включенные конденсаторы) или индуктивные контуры (например, при параллельно соединенных катушках), то свободная составляющая в таких цепях содержит постоянное слагаемое, которому отвечает нулевой корень l k = 0 (точка 4 на рис. 17.1, а ). Физический смысл таких составляющих определяется тем, что при наличии емкостного сечения в цепи возможно сколь угодно длительное существование постоянного заряда на конденсаторах сечения, а в индуктивном контуре возможно сколь угодно длительное протекание постоянного тока. Постоянные слагаемые в таких цепях появляются лишь в выражениях для напряжений конденсаторов емкостного сечения или токов индуктивного контура. В выражения других токов и напряжений той же цепи эти слагаемые не входят. Существование таких решений связано с идеализацией свойств элементов цепи — пренебрежением потерями в реальных катушках и проводимостью утечки реальных конденсаторов. В активных цепях, включающих управляемые источники, возможно появление неустойчивых, нарастающих во времени составляющих переходного процесса. Этот вопрос будет рассмотрен в Лекции 23.

В простейших цепях ограниченное число корней полностью определяет характер переходного процесса. Так, процесс в цепи первого порядка не может быть колебательным, так как такому процессу соответствует комплексно-сопряженная пара. Процессы в цепи второго порядка носят либо апериодический (при вещественных различных или кратном корнях), либо колебательный характер (при комплексно сопряженных корнях).

В пассивной цепи третьего порядка один корень характеристического уравнения всегда отрицательный вещественный, а два других либо образуют комплексно сопряженную пару, либо также являются отрицательными вещественными. Соответственно и свободные составляющие переходного процесса содержат апериодические слагаемые и не более одного колебательного слагаемого. В цепях более высокого порядка возможны несколько видов собственных колебаний, которым отвечают различные пары комплексно сопряженных корней, а также несколько апериодических составляющих, соответствующих различным вещественным корням.

В пассивных цепях, все корни которых имеют отрицательные вещественные части (точки 1 и 2 на рис. 17.1, а ), переходный процесс имеет затухающий характер, и установившийся режим x ‘( t ) при t ® ¥ не зависит от начальных условий, а определяется лишь структурой и элементами цепи и действующими в ней источниками. С другой стороны, свободные составляющие переходного процесса x» ( t ) существенно зависят от условий, имеющих место в цепи в момент коммутации — при t = 0 . При определенных начальных условиях отдельные свободные слагаемые могут отсутствовать — соответствующие им постоянные A k равны нулю. Возможно, в частности, такое сочетание начальных условий и параметров внешних источников, при котором начальные значения всех переменных состояния x (0) равны значениям установившихся решений в этот момент времени х ‘(0). В таких случаях переходная составляющая x «( t ) равна нулю, и в цепи сразу с момента коммутации t = 0 наступает установившийся режим. Возможность подобных ситуаций в простейших RC — и RL -цепях была установлена ранее в п. 15.2 и 15.3.

Дальше
Перейти к задачам по теме данной лекции
Дальше
Обратно к плану лекции

Операторный метод для действительных корней.

Составим операторную схему замещения (рис.3.4.4).

До коммутации тока в катушке и напряжения на конденсаторе не было. Это значит, что в цепи нулевые начальные условия u_C(0) = 0 и i₁(0) = 0. Изображение тока i(t) I(p)запишем по законуОма:

, где р = σ+jω – оператор Лапласа.

Изображение постоянного напряжения U есть

.

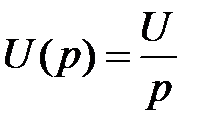
Операторное сопротивление Z(p) равно

.

(3.5)

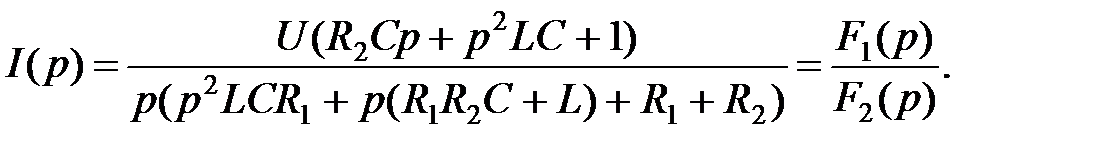
Подставив числовые значения, получим :

Изображение тока представляет собой отношению двух функций переменного р, причем степень многочлена F₂(р)больше степени многочлена F₁(p), то есть I(p) представляет собой правильную дробь.

Для того чтобы вычислить оригинал — ток i(t), нужно вос­пользоваться формулой разложения. С этой целью нужно сначала найти корни знаменателя. К двум корням, которые мы вычислили в классическом методе: p₁ = -9420 р₂ = -1380 , добавился третий корень р₃ = 0. Наличие нулевого корня свидетельствует о существовании принужденной составляющей.

Оригинал тока находим, используя формулу разложения:

Определим производную знаменателя:

.

Результат идентичен полученному классическим методом.

На примере той же схемы (рис.3.4.1) рассмотрим случай комплексно-сопряженных корней.

L = 50 мГн =5·10 -2 Г

С = 8 мкФ = 8·10 -6 Ф

Классический метод для комплексно-сопряженных корней.

Ищем решение для тока i₁(t)как сумму принужденной и свободной составляющих

Принужденные составляющие определяются в установившемся режиме

.

Корни характеристического уравнения находим из выражения (3.2):

.

Подставляя значения параметров, получим:

Так как корни комплексно-сопряженные, свободную составляющую ищем в виде:

Здесь δ = 2250, ω_св = 1561,25, тогда

i₁(t) = 1,467 +

Для определения постоянных А₁ и γ запишем производную тока i₁(t)

В момент времени t = 0 согласно условий (3.1) и (3.3) имеем:

i₁(t) = 0 и .

Постоянные определяем, решая систему уравнений для тока и его производной в момент времени t = 0.

Из первого уравнения:

.

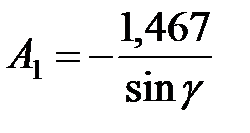
Подставляем А₁ во второе уравнение:

,

.

Для определения тока i₂(t) запишем уравнения для независимой переменной u_C(t) и ее производной:

В начальный момент времени t = 0 по условию (3.1) u_C(t) = 0, производная, согласно (3.4) равна

С учетом этого для t = 0 имеем:

.

Из первого уравнения:

.

Подставляем во второе уравнение

Отсюда

=C[ ]=

Преобразуем выражение в квадратных скобках.

Окончательно ток запишется:

Ток в неразветвленной части цепи:

Преобразуем выражение в скобках.

.

Операторный метод для комплексно-сопряженных корней.

Ток в неразветвленной части цепи определится выражением (3.5)

Подставив числовые значения, получим :

Находим корни уравнения F₂(p) = 0.

Так как корни комплексно-сопряженные, оригинал тока находим, используя формулу разложения:

(3.6)

.

Подставляем полученные выражения в формулу (3.6)

Используя правила тригонометрии, преобразуем

Окончательный результат

Требования к защите курсовой работы.

При защите работы студент должен уметь грамотно объяснить последовательность выполнения расчетов, рассказать, какими правилами и законами электрических цепей он воспользовался на каждом этапе расчетов, обосновать правомерность их применения, и уметь демонстрировать их на других примерах.

Оценка за курсовую работу ставится по итогам защиты.