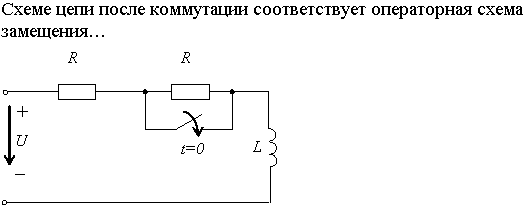
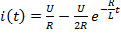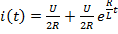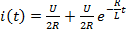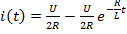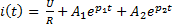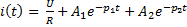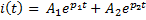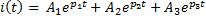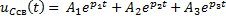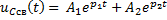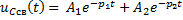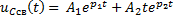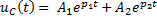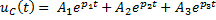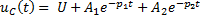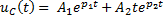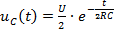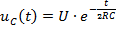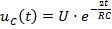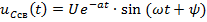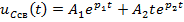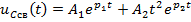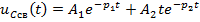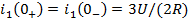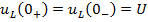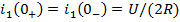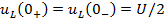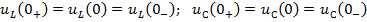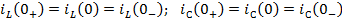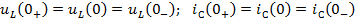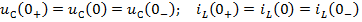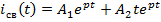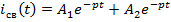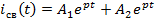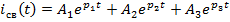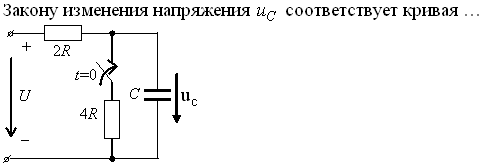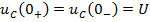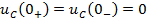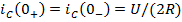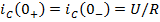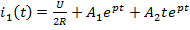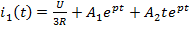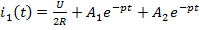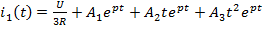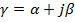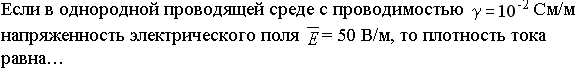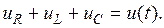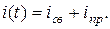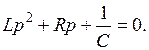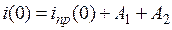ДИДАКТИЧЕСКАЯ ЕДИНИЦА № 4
Дисциплина «Теоретические основы электротехники»
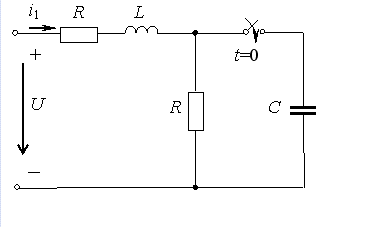
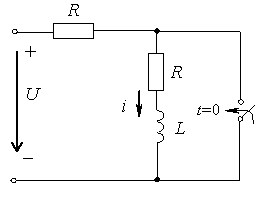
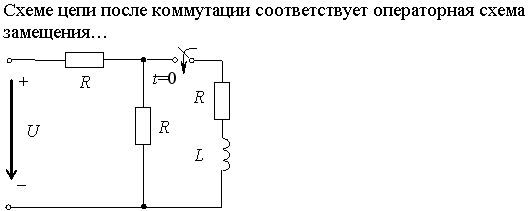
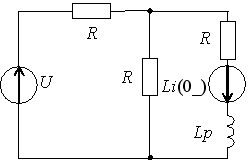
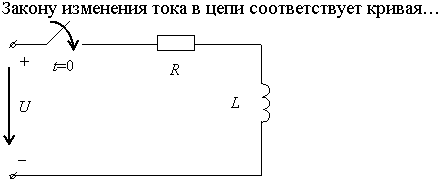
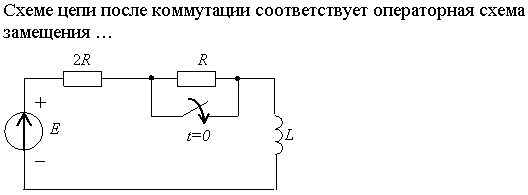
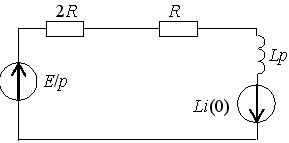
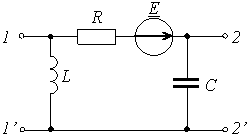
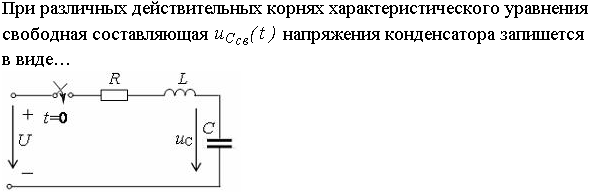
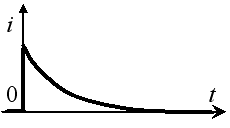
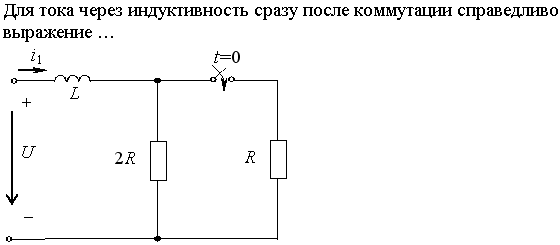
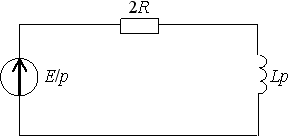
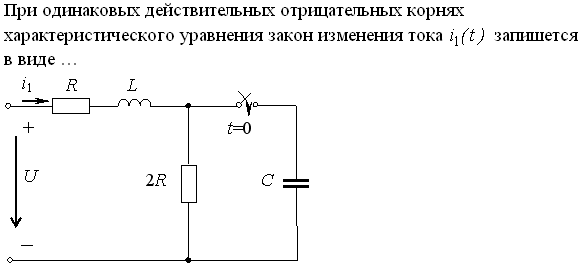
Задание 2.Ток i изменяется во времени так…
1) i(t)=U/2R – (U/2R) e -R/L· t
2) i(t)=0 – (U/2R) e -R/L·t
3) i(t)=U/2R + (U/2R) e -R/L·t
*4) i(t)=0 + (U/2R )e -R/L· t
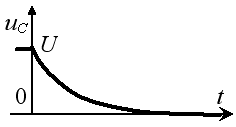
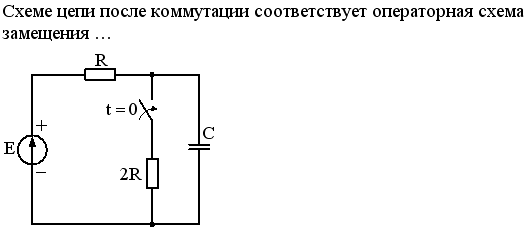
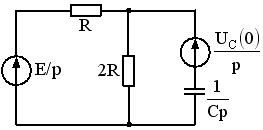
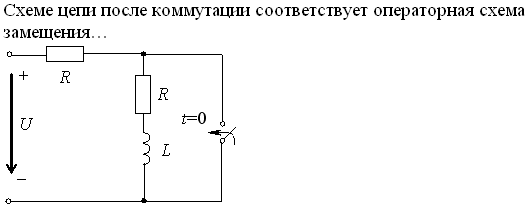
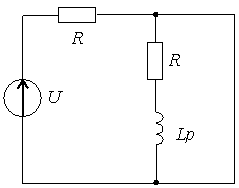
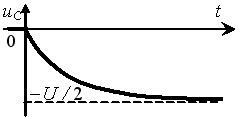
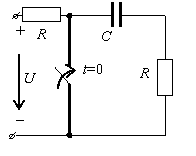
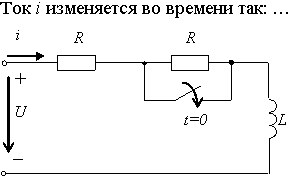
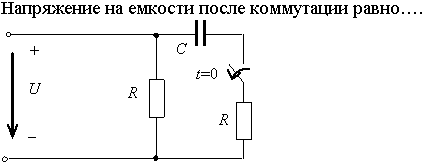
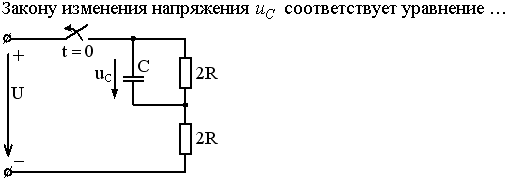
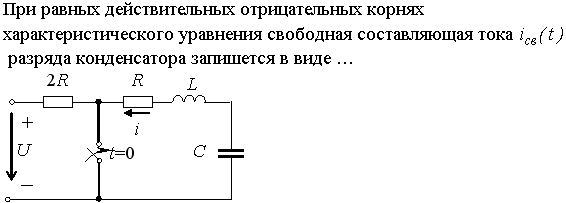
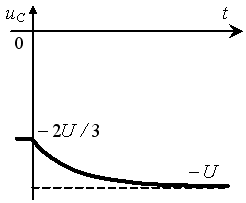
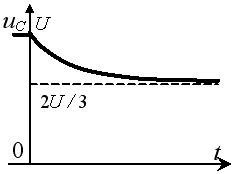
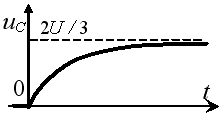
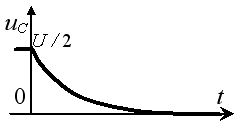
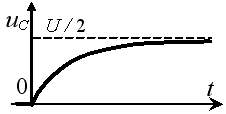
Задание 3.Напряжение на емкости после замыкания ключа равно…
*1)
2)
3)
4)
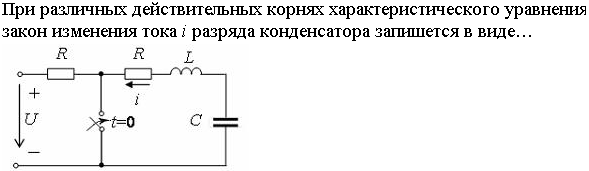
1)
2)
*3)
4)
Задание 6
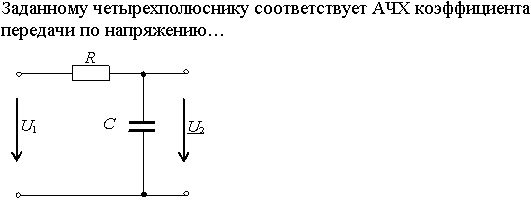
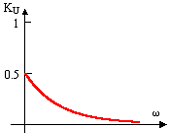
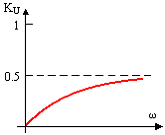
Задание 7.Если у симметричного четырехполюсника при входном напряжении U1=200 В напряжение на выходе U2=50 В, то при перемене местами входных и выходных зажимов входное и выходное напряжения соответственно равны…
1)
*2)
3)
4)
Задание 9
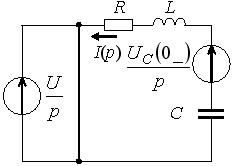
Задание 10
1) 
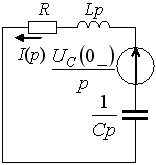
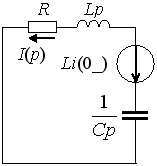
Задание 11
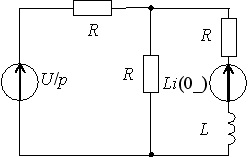
1) 
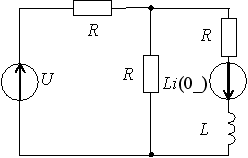
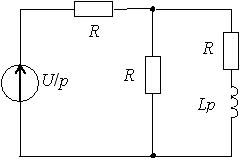
Задание 12
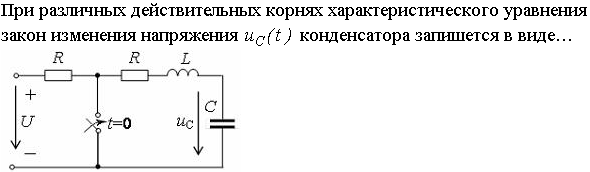
2)
3)
4)
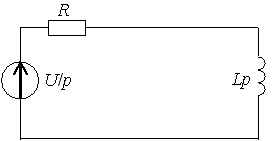
Задание 13
1) 
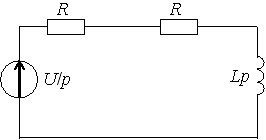
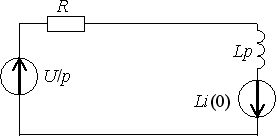
Задание 14
1) 


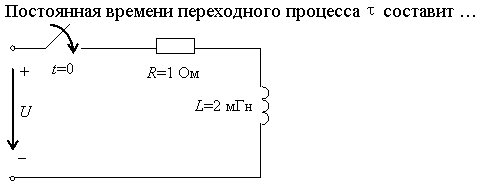
Задание 15. В операторном методе для перехода от изображений токов и напряжений к оригиналам этих величин (функциям времени) используют…
1) матричные преобразования 3) взятие интегралов для вещественных чисел
2) вычисление производных *4) таблицы соответствия изображений и оригиналов,
*1)
2)
3)
4)
Задание 17
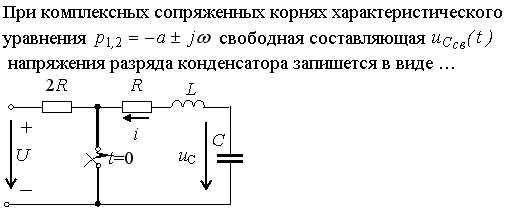
Задание 18
2)
3)
4)
Задание 19
2)
*3)
4)
Задание 20
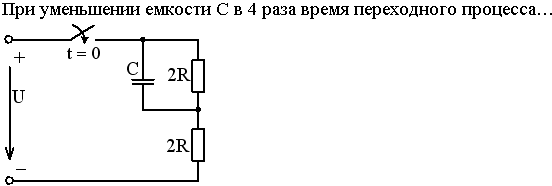
2) уменьшится в 2 раза
3) увеличится в 4 раза
4) увеличится в 2 раза
Задание 21.Законы коммутации записываются выражениями…
1)
2)
3)
*4)
Задание 22
*1) 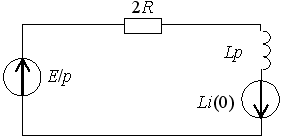
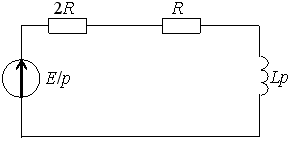
Задание 23
2)
3)
4)
Задание 24
1) 
Задание 25

2)
3)
4)
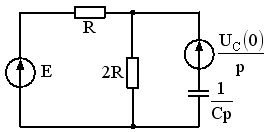
Задание 26
1) 
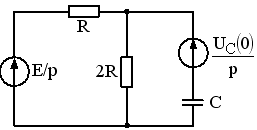
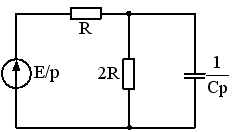
1)
*2)
3)
4)
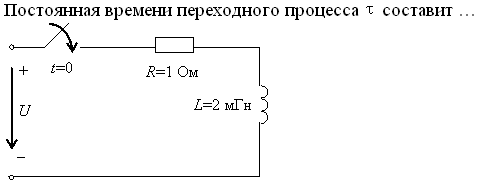
Задание 28
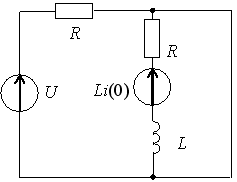
Задание 29
1) 
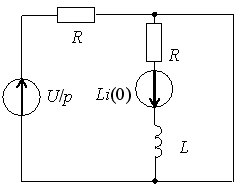
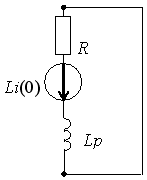
Задание 30
1) 
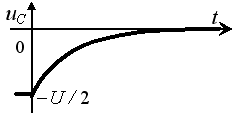
ДИДАКТИЧЕСКАЯ ЕДИНИЦА № 5
Дисциплина «Теоретические основы электротехники»
Задание 1. Для сопротивлений холостого хода и короткого замыкания пассивного четырехполюсника справедливо…
Задание 2.Для линейных четырехполюсников токи I1 и I2 выражаются через напряжения U1 и U2 с помощью уравнений, записанных в …
1) Z – форме 2) H – форме 3) A – форме *4) Y – форме
Задание 3.Еслив длинной линии отсутствует отраженная волна, то линия…
1) нагружена чисто реактивным сопротивлением
2) на конце разомкнута
3) является неискажающей
*4) нагружена волновым сопротивлением
Задание 4.Характеристическими параметрами четырехполюсника являются параметры…
1) Z10 , Z20 2) Z1k , Z2k 3) Zвх1 , Zвх2 *4) Z1с , Z2c ,
Задание 5
Если для симметричного четырехполюсника А = 0,5 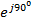
*1) С = –0,125 См; D = 0,5 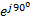
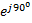
Задание 6
Если для токов и напряжений в начале *1) нагружена волновым сопротивлением
и в конце линии выполняется соотношение 2) на конце замкнута накоротко
U1/U2 = I1/I2, то линия… 3) без искажений, нагрузка любая
4) нагружена чисто реактивным сопротивлением
Задание 7
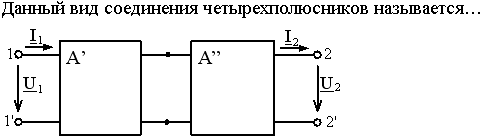
Задание 8.Режим согласованной нагрузки характеризуется…
*1) максимальной мощностью в нагрузке
2) максимальным напряжением на входе
3) максимальным входным током
4) максимальным коэффициентом полезного действия
Задание 9.Активный четырехполюсник изображен на схеме…
1) 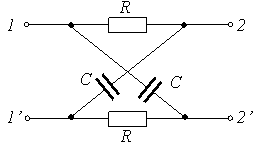
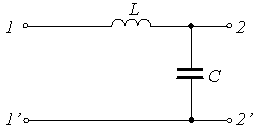
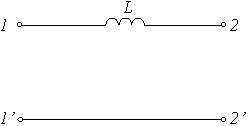
Задание 10.Количество возможных систем параметров, связывающих входные и выходные токи и напряжения четырехполюсника, равно…
1) 3 2) 5 3) 4 *4) 6
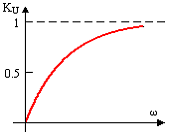
Задание 11.Если в середине линии, нагруженной волновым сопротивлением, фаза напряжения отличается от фазы входного напряжения на 60 0 , то фаза напряжения на выходе линии отличается от фазы входного напряжения на…
1) –45 0 *2) 120 0 3) 0 0 4) –90 0
Задание 12
1) 0,02 А/м 2 2) 5000 А/м 2 3) 1 А/м 2 *4) 0,5 А/м 2
Задание 13

Задание 14. Если в линии без потерь со скоростью света распространяется сигнал с частотой f = 10 МГц, то длина волны в линии равна…
*1) 30 км 2) 300 км 3) 3 км 4) 30 км
Задание 15. Для линейных четырехполюсников уравнения в Н –форме позволяют выразить…


3) j 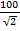
*1) 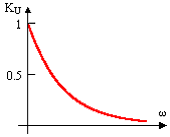
Задание 19.Чтобы записать уравнения симметричного четырехполюсника, связывающие токи и напряжения на его входных и выходных зажимах, необходимо задать ________ параметр(а).
1) 2 *2) 3 3) 4 4) 1
Задание 20
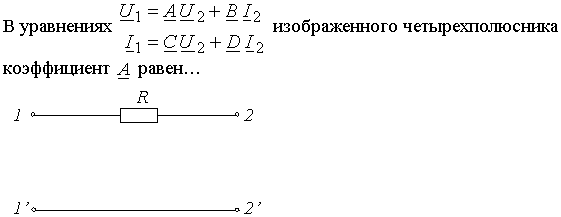
Задание 21.Если в линии без потерь со скоростью света распространяется периодический сигнал, имеющий длину волны 30 м, то период сигнала равен…
1) 1 мс *2) 0,1 мкс 3) 10 мкс 4) 1 мкс
1) сопротивлениями короткого замыкания
2) сопротивлениями холостого хода
Задание 23
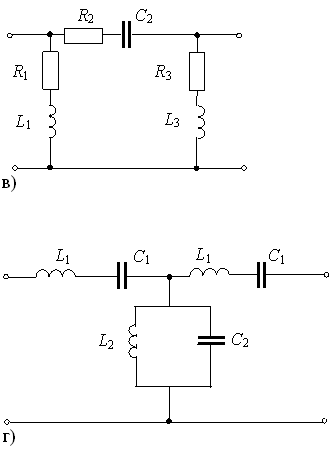
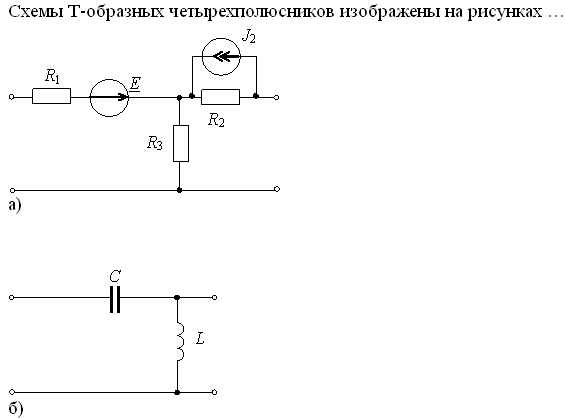

Задание 25.Если поменять местами входные и выходные зажимы пассивного четырехполюсника, то в уравнениях четырехполюсника…
1) изменят знак А и С 3) все А параметры изменят знак
2) ничего не изменится *4) поменяются местами А и D
Переходной процесс в цепи второго порядка
5 ПЕРЕХОДНОЙ ПРОЦЕСС В ЦЕПИ ВТОРОГО ПОРЯДКА
Рисунок 5.1 — Схема цепи
Уравнение цепи имеет вид

Дифференцируя обе части выражения (5.1), получим уравнение второго порядка для тока i в цепи:

Однородное уравнение, определяющее свободный ток, можно записать

Введем обозначения 





Ток переходного режима

Ток установившегося режима 

Произвольные постоянные интегрирования A1 и A2 определяют из начальных физических условий: 
Для определения постоянных A1 и A2 надо знать значение тока и всех его производных до (n – 1) включительно в начальный момент времени. В данном случае необходимо знать начальное значение тока и его первой производной. Начальное значение первой производной тока находится из уравнения цепи (5.1) при (t = 0)

где u(0) – значение приложенного напряжения u(t) при t = 0.
Из последнего уравнения получаем

Из уравнения (5.8) для производной тока имеем

Уравнения для нахождения постоянных интегрирования

где 
В качестве примера рассмотрим расчет переходного процесса классическим методом для схемы, изображенной на рис. 5.2. Определить ток
Рисунок 5.2 — Расчетная схема
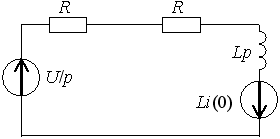
1. Для цепи после коммутации составляются уравнения по I и II законам Кирхгофа.
2. Определяются независимые начальные условия 


3. Искомая величина записывается в виде

4. Установившуюся составляющую определяют из расчета режима цепи после коммутации 
5. Составляется характеристическое уравнение, и определяются его корни

Корни могут быть:
действительные разные p1 и p2; действительные равные p1 = p2 = p; комплексно сопряженные 
где б – коэффициент затухания;
щсв – угловая частота свободных колебаний.
6. В соответствии с полученными корнями характеристического уравнения записывается свободная составляющая:
1) 
2) 
3) 

7. Искомое решение для первого случая

8. Определяются постоянные интегрирования A1 и A2:


Уравнения п.1 для момента времени t = 0 запишутся как

Независимые начальные условия i(0) и 

Для определения 
9. После определения постоянных интегрирования A1 и A2 подставляют их в искомое решение и расчет окончен.
Для определения других токов и напряжений не требуется выполнять все этапы расчета. Можно использовать известные выражения

В этом случае приложенное напряжение, а также ток установившегося режима равны нулю:

Для определения произвольных постоянных интегрирования в уравнении необходимо положить: 
Рисунок 5.3 — Расчетная схема
Обозначим 


Напряжения на катушке и конденсаторе

При выводе последнего уравнения учитывалось, что 
5.1 Корни характеристического уравнения
Характер процессов при разряде конденсатора оказывается различным в зависимости от того, будут ли корни характеристического уравнения вещественными или комплексными, что определяется соотношениями между параметрами R, L и C.
Рассмотрим возможные случаи.
1. Пусть корни характеристического уравнения вещественны и отличны друг от друга. Это имеет место при условии

Так как 





Ток i не меняет своего направления, т. е. конденсатор все время разряжается. Такой односторонний разряд конденсатора называют апериодическим. Кривые изменения напряжений показаны на рис. 5.5.
Переходные процессы в цепи, содержащей R-, L-, и С-элементы
Рассмотрим последовательную цепь, то есть простейшую цепь, содержащую резистивный индуктивный и емкостный элементы (рис. 11.10).
Рассмотрим общий случай входного напряжения u = u(t).
Составим уравнение состояния для этой цепи. Согласно второму закону Кирхгофа имеем:
В данной схеме две независимые переменные – ток индуктивности, который является общим для всей цепи, и напряжение на емкости, поэтому для определения переходных напряжений и тока дифференциальное уравнение можно составлять для любой из этих переменных.
Поскольку через все элементы протекает один и тот же ток, удобнее все напряжения выразить через ток
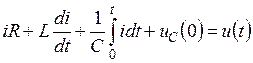
В это уравнение ток входит в алгебраической, дифференциальной и интегральной формах. Чтобы свести ток к одной форме, продифференцируем уравнение то времени:
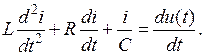
Получили дифференциальное уравнение второго порядка для тока в цепи.
Следует отметить, что порядок уравнения определяется количеством накопителей энергии в цепи. В данном случае имеется два накопителя энергии – индуктивность и емкость, следовательно, получаем дифференциальное уравнение второго порядка.
Решение этого уравнения ищем в виде суммы свободной и принужденной составляющих.
Принужденная составляющая определяется в установившемся режиме при t = ∞ и либо равна нулю 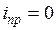
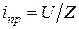
Для определения свободной составляющей составляем характеристическое уравнение. Рассмотрим два способа.
1. В уравнении (11.3) приравниваем нулю источники и заменяем символ дифференцирования 
Запишем это уравнение в приведенном виде:
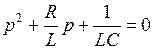
2. Запишем уравнение для комплексного сопротивления цепи и приравняем его нулю
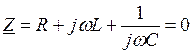
Сделаем замену 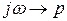
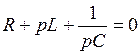
Приведем это выражение к общему знаменателю
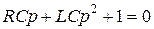
Запишем приведенное уравнение
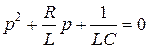
Получили такое же уравнение, как и в первом случае.
Найдем корни характеристического уравнения
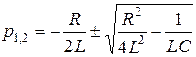
Проанализируем это выражение. При расчете корней характеристического уравнения возможны три случая.
1. Корни действительные, различные
Если дискриминант больше нуля, а это возможно в том случае, если
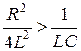
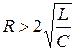
то корни будут действительными и различными по величине р1 ≠ р2. В этом случае решение дифференциального уравнения для свободной составляющей ищем в виде
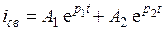
Переходной процесс при этом будет апериодическим. График переходного процесса показан кривой 1 на рис. 11.11.
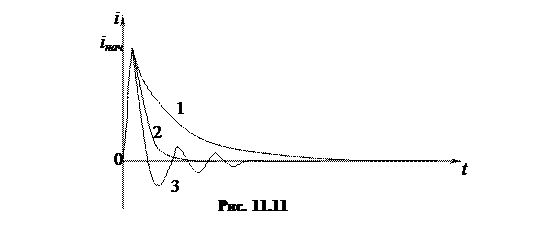 |
2. Корни действительные, равные
Действительные и равные по величине корни р1 = р2 = р будут в том случае, если дискриминант равен нулю, то есть, если
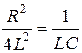
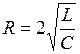
В этом случае решение для свободной составляющей тока ищем в виде
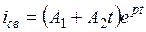
Переходной процесс также будет апериодическим, но это предельный или критический режим (кривая 2 на рис. 11.11).
3. Корни комплексно-сопряженные
Такой режим будет в том случае, если дискриминант отрицательный, то есть
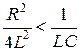
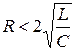
Корни характеристического уравнения
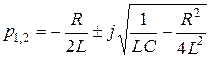
В этом случае переходной процесс будет затухающим колебательным, то есть ток будет изменяться относительно принужденной составляющей по синусоидальному закону с затухающей амплитудой (кривая 3 на рис. 3.11). Решение для свободной составляющей ищем в виде
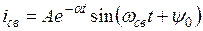
В этом выражении ввели следующие обозначения:
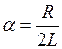
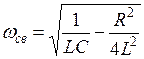
Скорость затухания тока характеризуется декрементом колебаний, равным отношению двух последующих амплитуд
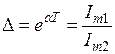
где Т = 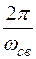
Чаще пользуются логарифмическим декрементом колебаний
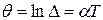
При любом характере корней свободная составляющая содержит две постоянных интегрирования, то есть две неизвестных величины, для определения которых необходимо составить два уравнения.
Для определения постоянных интегрирования необходимо знать значение тока и всех его производных в начальный момент времени.
Выражения для полного тока и его производной имеют вид:
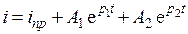

Запишем исходное уравнение (11.2) при t = 0
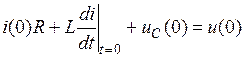
Напряжение источника и(0), как правило, известно; i(0) и иС(0) – независимые начальные условия, определяемые по состоянию цепи до коммутации и законам коммутации.
Из этого выражения можно найти
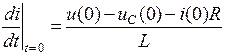
При t = 0 имеем:
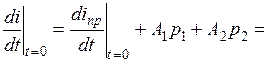
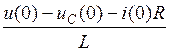
Решая эти уравнения относительно А1 и А2, находим постоянные интегрирования.
Рассмотрим частные случаи переходных процессов в R-, L-, C-цепи.
http://pandia.ru/text/81/139/65824.php
http://lektsii.org/5-47854.html