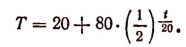Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение показательных уравнений.
Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение
Немного теории.
Показательная функция, её свойства и график
Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m
4) (ab) n = a n b n
7) a n > 1, если a > 1, n > 0
8) a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \( a \neq 1\)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.
3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.
Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2
Решить уравнение 3 х + 1 — 2 • 3 x — 2 = 25
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 (3 3 — 2) = 25, 3 х — 2 • 25 = 25,
откуда 3 х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2
Решить уравнение 3 х = 7 х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac<3^x> <7^x>= 1 \), откуда \( \left( \frac<3> <7>\right) ^x = 1 \), х = 0
Ответ х = 0
Решить уравнение 9 х — 4 • 3 х — 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 — 4t — 45 = 0. Решая это уравнение, находим его корни: t1 = 9, t2 = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2
Решить уравнение 3 • 2 х + 1 + 2 • 5 x — 2 = 5 х + 2 х — 2
Запишем уравнение в виде
3 • 2 х + 1 — 2 x — 2 = 5 х — 2 • 5 х — 2 , откуда
2 х — 2 (3 • 2 3 — 1) = 5 х — 2 ( 5 2 — 2 )
2 х — 2 • 23 = 5 х — 2 • 23
\( \left( \frac<2> <5>\right) ^
x — 2 = 0
Ответ х = 2
Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
Показательные уравнения в математике с примерами решения и образцами выполнения
Простейшее показательное уравнение — это уравнение вида 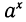
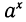
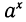
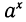
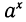
Сформулируем общий результат о решении простейшего показательного уравнения (схема XI).
Теорема:
Пусть а > 0 и а ≠ 1. Уравнение 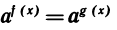
Доказательство:
Докажем, что если 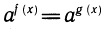
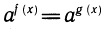
Примеры:
Простейшее логарифмическое уравнение — это уравнение вида logax=b. Оно имеет единственное решение х — а при любом b.
Сформулируем общий результат о решении простейшего логарифмического уравнения (схема XI).
Теорема:
Уравнение ioga f (х) = loga g (х) равносильно уравнению f(x)=g(x) при ограничениях f (х)> 0, g(x)>0.
Доказательство:
Пусть х — решение уравнения
Тогда определены логарифмы чисел f (х) и g (х), т. е. эти числа должны быть больше нуля. Потенцируя равенство 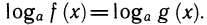
Примеры:
Мы решили уравнение х— 1 = 5 — х, а затем проверили, удовлетворяет ли решение условиям х— 1 >0 и 5 — х>0. Заметим, что если f (x) = g (х) и f (х)>0, то тогда и g (x)>0, т. е. из двух неравенств достаточно проверить только одно.
Показательные уравнения справочные сведения
Показательная функция 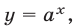
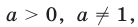
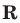
2.Для любых 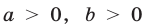
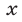
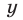
3. Простейшее показательное уравнение
не имеет корней при 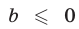
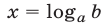
В частности, уравнение 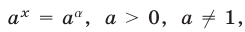
4.Уравнение
5.Уравнение
равносильно каждому из уравнений
Примеры с решениями
Пример:
Решить уравнение
Решение:
Данное уравнение равносильно каждому из уравнений 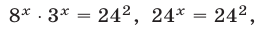
Ответ.
Пример:
Решить уравнение
Решение:
Это уравнение равносильно каждому из уравнений:
откуда находим
Ответ.
Пример:
Решение:
Пусть 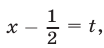
Это уравнение равносильно каждому из уравнений: 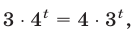
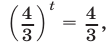
Ответ.
Пример:
Решение:
Полагая 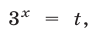
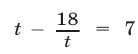
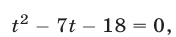
Следовательно, исходное уравнение равносильно совокупности уравнений 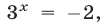
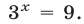
Ответ.
Пример:
Решение:
Запишем данное уравнение в виде
и заметим, что левая часть уравнения (2) — однородный многочлен степени 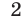
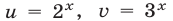
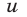
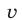
Разделив обе части уравнения (2) на 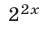
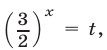
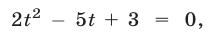
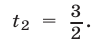
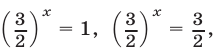
Ответ.
Пример:
Решение:
Воспользуемся равенством 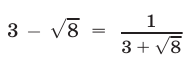
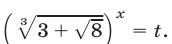
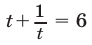
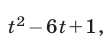
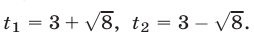
откуда
Ответ,
Пример:
Решение:
Число 2 является корнем этого уравнения. Докажем, что уравнение не имеет других корней. Так как каждая из функций 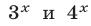
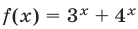
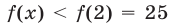
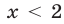
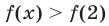
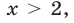
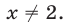
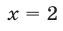
Показательные неравенства
Простейшее показательное неравенство — это неравенство вида 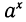
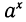
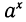
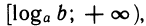
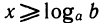
Пусть а>1 и b ≤ 0. Решением неравенства 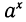
Можно сказать, что неравенство типа 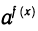
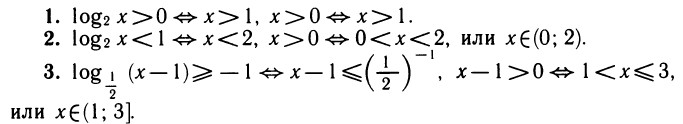
4. 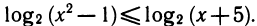
Основной прием, с помощью которого решают показательные и логарифмические уравнения и неравенства,— это введение новой неизвестной. Поясним этот прием на ряде примеров.
1) Выражение показательных функций друг через друга.
Рассмотрим выражения 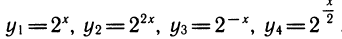
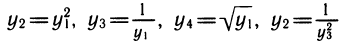
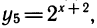
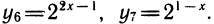
К этому полезно напомнить связь между различными основаниями. Например, 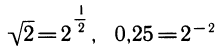
также нетрудно выразить через у1:
Если в уравнении или неравенстве встречается несколько показательных функций, то надо все их выразить через одну. Обычно после этого показательное уравнение или неравенство превращается в алгебраическое.
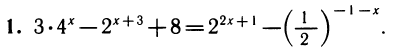
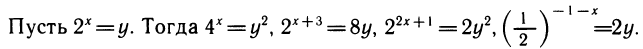
Делаем замену 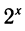
(мы умножили неравенство на у, что можно, так как
Так как 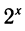
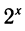
Используя модуль перехода, легко связать эти выражения между собой:
Свойства логарифмов позволяют по-разному записать связи между выражениями. Например,
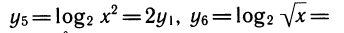
Если в уравнении или неравенстве встречается несколько логарифмических функций, то надо (если не удается избавиться от логарифмов потенцированием) выразить их через одну и свести логарифмическое уравнение или неравенство к алгебраическому.
Делаем замену lg х = у. Получаем уравнение относительно у:
Возвращаясь к неизвестной х, получим lg х = 2, х=100; lgx = 3, х= 1000.
Перейдем к основанию 3. Получим
заменив log3x на у, получим
Возвpащаясь к неизвестной х, получим log3x = 2, x = 9; log3x =—2,
Ответ:
Логарифмируя, получим равносильное данному неравенство (lg x —2) 1g x ≤ 3.
Положим lg х = у. Получим неравенство (у — 2)y ≤ З ⇔
Возвращаясь к неизвестной х, получим — l ≤ lg x ≤ 3 ⇔ 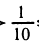
Ответ: 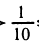
Использование свойства монотонности функций при решении показательных уравнений
Монотонность функций часто позволяет определить число корней уравнения, а иногда и найти их значения. Рассмотрим примеры решения уравнений.
В левой части уравнения имеем возрастающую функцию, а в правой — убывающую. Следовательно, уравнение не может иметь более одного корня (рис. 111). Один корень можно угадать: х=1. Это число и является окончательным ответом.
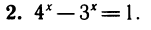
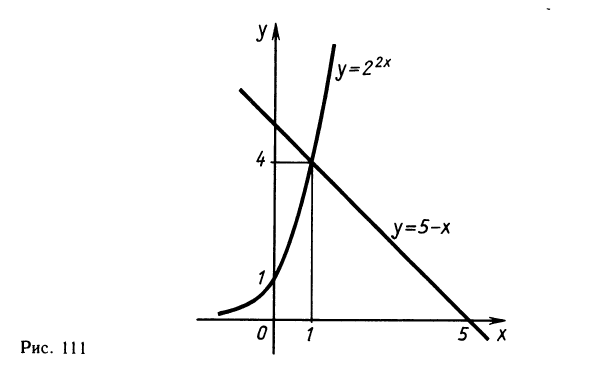
Одно решение х=1 легко найти подбором. Докажем, что других корней нет. Перепишем уравнение так:
В правой части последнего уравнения сумма убывающих функций т. е. значение у = 1 эта сумма может принять только один раз.
3. Сколько корней имеет уравнение 
Изобразим схематически графики функций у = 
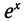
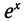
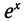
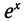
Ответ: при 0 ≤ а е два корня, при а = е один корень, при корней нет.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
Показательные уравнения и примеры решения
Определение. Уравнение называется показательным, если неизвестная входит в показатель степени.
Рассмотрим простейшие приемы решения показательных уравнений на отдельных примерах.
1. Решить уравнение
Представим левую и правую части уравнения в виде степеней, имеющих одинаковые основания:
Отсюда 3х = 2, или 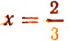
Мы здесь воспользовались следующей теоремой:
Если степени равны и основания равны, положительны и отличны от единицы, то равны и их показатели степеней.
Докажем эту теорему.
Пусть а > 1 и 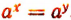
Допустим противное тому, что требуется доказать, т. е. допустим, что х > у или что х
3. Решить уравнение
Преобразуя левую часть уравнения, получим:
Значит, данное показательное уравнение имеет два корня:
4. Решить уравнение
Примем за новую неизвестную выражение 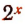
либо 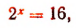
Из уравнения 
Из уравнения 
Итак, данное показательное уравнение имеет два корня: 4 и — 2.
5. Решить уравнение
Снова, обозначая 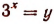
Таким образом, получим:
Как было указано при исследовании показательной функции, степень 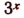
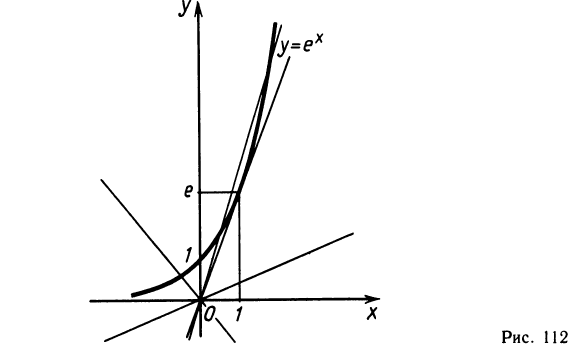
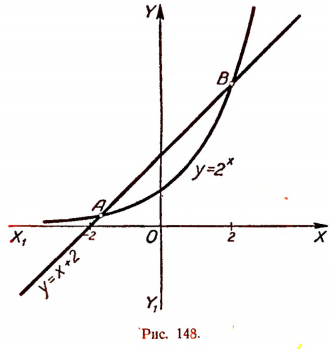
6. Решить уравнение
Для решения этого уравнения применим графический метод. Построим на одной координатной плоскости (рис. 148) графики функций:
Тогда абсциссы точек пересечения этих линий, т. е. абсциссы точек А и В, будут корнями данного уравнения. Абсцисса точки В, равная числу 2, будет точным корнем данного уравнения, а абсцисса точки А, равная приближенно —1,7, будет его приближенным корнем. Других корней данное уравнение не имеет.
Сведения, изложенные в этой главе, окажутся полезными при изучении логарифмов, которым посвящена следующая глава.
Примем к сведению без доказательства еще следующую теорему:
Если а есть положительной число, отличное от единицы, а N — любое положительное число, то уравнение 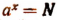
Примеры. Уравнение 
Уравнение 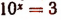
Итак, мы можем сделать следующие заключения:
- Выражение
, где а>0, имеет при каждом действительном значении х одно и только одно действительное значение.
- Действия над выражениями вида
, в которых х является любым действительным числом, можно выполнять по тем же правилам, по которым они выполняются над степенями с целым положительным показателем. Поэтому выражение
при всяком действительном значении х также называется степенью (обобщенной).
Примеры зависимостей, выражающихся с помощью показательных функций.
1. 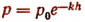
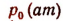
k —некоторая известная постоянная;
е —2,718;
h(м) —высота над уровнем моря;
р(ат) —давление на высоте А над уровнем моря.
Здесь h есть независимая переменная, или аргумент, а р есть зависимая переменная, или функция.
По этой формуле можно определять давление р по заданному значению h.
2. Если температура воздуха равна 20° С и тело в течение 20 минут охлаждается от 100 до 60°, то зависимость температуры Т охлаждающегося тела от времени t минут (в течение которого будет происходить охлаждение) выразится формулой
Здесь t есть аргумент, а Т—функция.
Пользуясь этой формулой, можно узнать, например, что через один час температура тела понизится до 30°.
Приведенные формулы выводятся в курсах высшей математики.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Показательные уравнения
О чем эта статья:
6 класс, 7 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательного уравнения
Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:
Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.
С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a
Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.
http://lfirmal.com/pokazatelnyie-uravneniya-primeryi-s-resheniem/
http://skysmart.ru/articles/mathematic/pokazatelnye-uravneniya
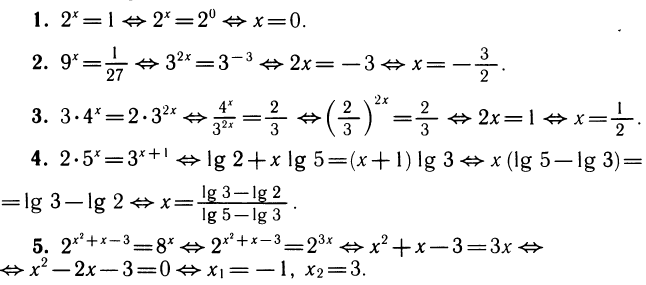
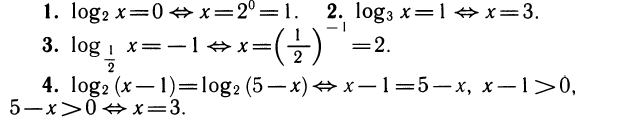
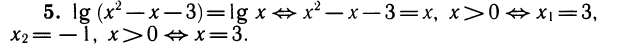

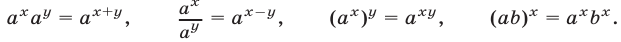
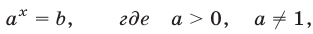
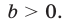
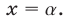
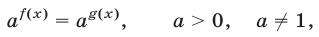
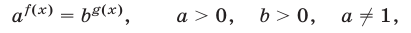
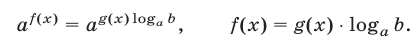
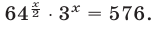
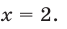
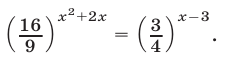
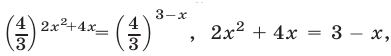
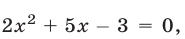
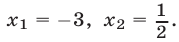
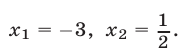
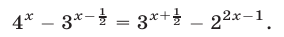
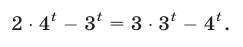
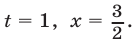
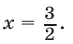
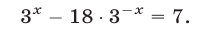
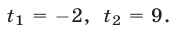
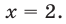
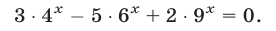
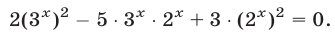
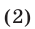
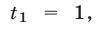
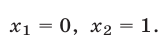
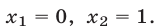
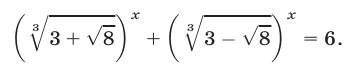
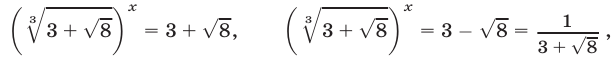
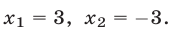
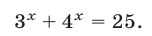
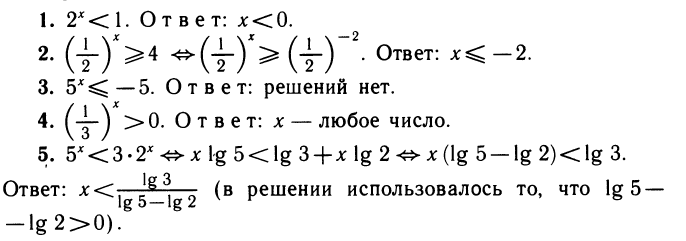
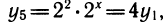
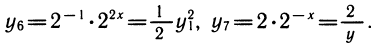
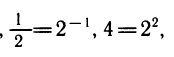
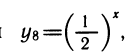
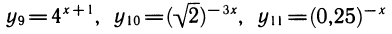
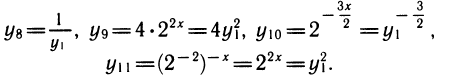
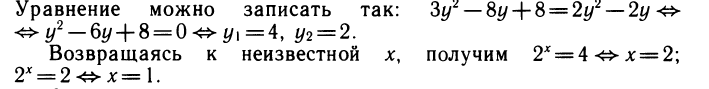
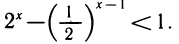
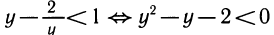

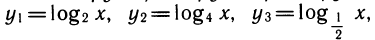
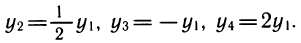
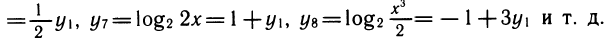
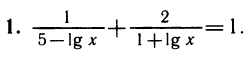
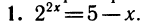
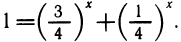
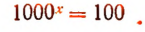
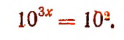
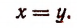

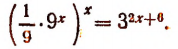
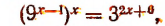

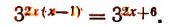
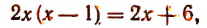
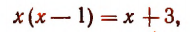
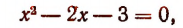
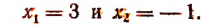
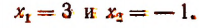
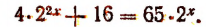
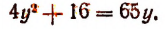
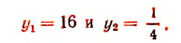
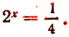
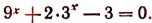
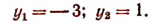
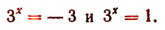
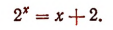
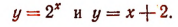
 , где а>0, имеет при каждом действительном значении х одно и только одно действительное значение.
, где а>0, имеет при каждом действительном значении х одно и только одно действительное значение.