При решении уравнения ctg 1

Простейшие тригонометрические уравнения с тангенсом и котангенсом

Чтобы уверенно решать простейшие уравнения с тангенсом или котангенсом нужно знать значения стандартных точек на круге и стандартные значения на осях тангенсов и котангенсов (если в этом материале есть пробелы, читайте « Как запомнить тригонометрический круг »).

Алгоритм решения простейших уравнений с тангенсом

Давайте с вами рассмотрим типичное уравнение, например, \(tg⁡x=\sqrt<3>\).

Пример. Решить уравнение \(tg⁡x=\sqrt<3>\).

Чего от нас здесь хотят? Чтобы мы написали все такие значения угла в Пи, для которых тангенс равен корню из трех. Причем написать надо именно все такие углы. Давайте нарисуем тригонометрический круг и ось тангенсов…

…и обозначим то место на оси, куда мы должны попасть в итоге.

Теперь найдем через какие точки на окружности мы должны идти, чтобы попасть в этот самый корень из трех –проведем прямую через начало координат и найденную точку на оси тангенсов.

Точки найдены. Давайте подпишем значение одной из них…

…и запишем окончательный ответ – все возможные варианты значений в Пи, находящиеся в отмеченных точках: \(x=\frac<π><3>+πn\), \(n∈Z\).

Замечание. Вы, наверно, обратили внимание, что в отличие от уравнений с синусом и косинусом , здесь записывается только одна серия корней, причем в формуле добавляется \(πn\), а не \(2πn\). Дело в том, что в любом уравнении с тангенсом решением получаются две точки на окружности, которые находятся друг от друга на расстоянии \(π\). Благодаря этому значение обеих точек можно записать одной формулой в виде \(x=t_0+πn\), \(n∈Z\).

Пример. Решить уравнение \(tg⁡x=-1\).

Итак, окончательный алгоритм решения подобных задач выглядит следующим образом:

Шаг 1. Построить окружность, оси синусов и косинусов, а также ось тангенсов.

Шаг 2. Отметить на оси тангенсов значение, которому тангенс должен быть равен.

Шаг 3. Соединить прямой линией центр окружности и отмеченную точку на оси тангенсов.

Шаг 4. Найти значение одной из точек на круге.

Шаг 5. Записать ответ используя формулу \(x=t_0+πn\), \(n∈Z\) (подробнее о формуле в видео), где \(t_0\) – как раз то значение, которые вы нашли в шаге 4.

Специально для вас мы сделали удобную табличку со всеми шагами алгоритма и разными примерами к нему. Пользуйтесь на здоровье! Можете даже распечатать и повесить на стенку, чтоб больше никогда не ошибаться в этих уравнениях.

Алгоритм решения простейших уравнений с котангенсом

Сразу скажу, что алгоритм решения уравнений с котангенсом почти такой же, как и с тангенсом.

Шаг 1. Вопрос у нас практически тот же – из каких точек круга можно попасть в \(\frac<1><\sqrt<3>>\) на оси котангенсов?
Строим круг, проводим нужные оси.

Теперь отмечаем на оси котангенсов значение, которому котангенс должен быть равен…

…и соединяем центр окружности и точку на оси котангенсов прямой линией.

По сути точки найдены. Осталось записать их все. Вновь определяем значение в одной из них…

…и записываем окончательный ответ по формуле \(x=t_0+πn\), \(n∈Z\), потому что у котангенса период такой же как у тангенса: \(πn\).

Кстати, вы обратили внимание, что ответы в задачах совпали? Здесь нет ошибки, ведь для любой точки круга, тангенс которой равен \(\sqrt<3>\), котангенс будет \(\frac<1><\sqrt<3>>\).

Разберем еще пример, а потом подведем итог.

Пример. Решить уравнение \(ctg⁡x=-1\). Здесь подробно расписывать не буду, так как логика полностью аналогична вышеизложенной.

Итак, алгоритм решения простейших тригонометрических уравнений с котангенсом:

Шаг 1. Построить окружность и оси синусов и косинусов, а также ось котангенсов.

Шаг 2. Отметить на оси котангенсов значение, которому котангенс должен быть равен.

Шаг 3. Соединить центр окружности и точку на оси котангенсов прямой линией.

Шаг 4. Найти значение одной из точек на круге.

Шаг 5. Записать ответ используя формулу \(x=t_0+πn\), \(n∈Z\), где \(t_0\) – как раз то значение, которые вы нашли в шаге 4. И табличка в награду всем дочитавшим до этого места.

Примечание. Возможно, вы обратили внимание, что при решении примеров 2 и 3 в обеих табличках мы использовали функции \(arctg\) и \(arcctg\). Если вы не знаете, что это – читайте эту статью.

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

1. Корни уравненияcosx=a.

При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a n arcsin a + 2πn, n ∈ Z (3)

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

1. Какие уравнения называют простейшими тригонометрическими?
2. Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
3. Выведите формулы решения простейших тригонометрических уравнений.
4. Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)

Урок «Тригонометрические уравнения»

Краткое описание документа:

Несколько уроков назад учащиеся уже начали изучать тригонометрические уравнения, рассмотрели разнообразные примеры.

В данной теме перейдем к их более углубленному изучению. В начале урока дается определение тригонометрического уравнения, указывается, какие уравнения относятся к простейшим тригонометрическим уравнениям:

Приводятся решения уравнений, которые были изучены ранее:

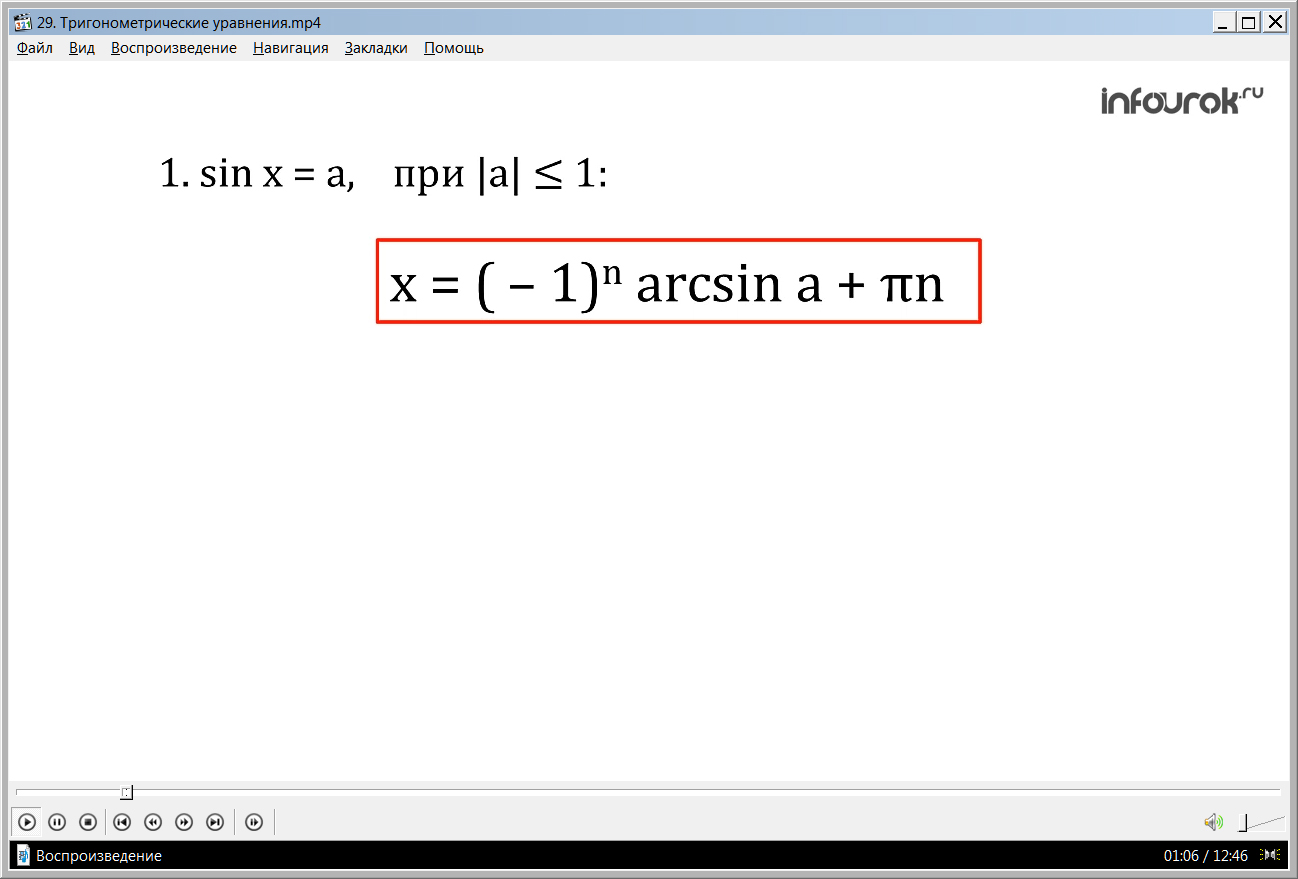
1) sin x = a, если модуль а меньше или равен единице, х = (– 1) n arcsin a + πn. Или: х = arcsin a + 2πk; х = π – arcsin a+ 2πk;

2) cos x = a, когда модуль а меньше или равен единице, x = ± arccos a + 2πn;

3) если модуль а больше единицы, то уравнения sin x = a и cos x = a не имеют решений;

4) tg x = a имеет решение для любого значения а, х = arctg а + πn;

5) ctg x = a имеет решение для любого значения а, х = arcctg а + πn;

6) в пункте отражены частные случаи решения уравнений sin x = a и cos x = a при а = 0, а = 1 и а = – 1, которые для наглядности представлены в таблице.

Далее рассмотрим примеры решений. Пример 1: решить уравнение, содержащее sin.

Для решения вводится новая переменная t, которая равна значению переменной под знаком sin, в данном случае t = 4x. Запишем исходное выражение, заменяя x на t. Определим, что модуль а меньше либо равен единице, а значит уравнение имеет решение вида х = (– 1) n arcsin a + πn. Напишем это выражение с помощью переменной t. По таблице значений найдем решение arcsin, зная которое, запишем значение t. Далее, подставив вместо t 4x, найдем ответ: х = (– 1) n π/16 + πn/4. Кстати, новую переменную можно не вводить и решать уравнение только с х; в нашем случае мы ввели новую переменную для удобства решения.

Пример 2. Найти такие решения уравнения, которые принадлежат интервалу от 0 до π/2. Дано такое же уравнение, как в примере 1. Из примера 1 выпишем х = (– 1) n π/16 + πn/4. Далее, подставляя вместо n целые числа, получим:

1) при n = 0: х = π/16; этот корень решения принадлежит промежутку от 0 до π/2;

2) при n = 1: х = 3π/16; это значение принадлежит отрезку от 0 до π/2;

3) при n = 2: х = 9π/16; это число не принадлежит интервалу от 0 до π/2, а также не будут принадлежать данному интервалу другие значения х при n > 2;

4) при n = – 1: х = – 5π/16; это значение не принадлежит промежутку от 0 до π/2, а также не будут принадлежать данному промежутку другие значения х при n n arcsin a + πn.

или эти решения можно записать по-другому

х = arcsin a + 2πk, х = π — arcsin a + 2πk.

1. Решения уравнения cosx=a, при | а | 1, имеют вид:

х = arccos a + 2πn.

1. Если | а | 1, то уравнения sinx=a и cosx=a не имеют решений.
2. Уравнение tg x = a имеет решение для любого значения а и эти решения имеют вид х = arctg x a + πn.
3. Уравнение ctg х = a имеет решение для любого значения а и эти решения имеют вид: х = arcсtg а + πn.
4. Важно помнить частные случаи:

Во всех формулах подразумевается, что nϵZ, kϵZ( эн и ка принимают любые целочисленные значения).

ПРИМЕР 1. Решить уравнение sin 4x= .

Решение. Введем новую переменную t = 4x, получим sin t = . Так как |а|= , значит | а | 1 и решение уравнения имеет вид х = (–1) n arcsina + πn.

Тогда t =(–1) n arcsin +πn ( тэ равно минус единица в степени эн умноженная на арксинус корня из двух на два плюс пи эн). А так как arcsin = , то

t = (–1) n +πn .Следовательно, 4х = (1) n +πn. Разделим обе части на четыре, получим х = (- 1) n +.(произведение минус единицы в степени эн и пи, деленного на шестнадцать плюс пи эн на четыре).

ЗАМЕЧАНИЕ. Необязательно вводить новую переменную. Можно сразу от уравнения sin 4x= переходить к уравнению 4х = (–1) n + πn.

ПРИМЕР 2. Найти те корни уравнения sin 4x= , которые принадлежат отрезку [0, ].

Решение. Как мы знаем из примера 1, решение уравнения sin 4x= записано в виде х=(–1) n +. Далее, придавая параметру n целочисленные значения и подставляя эти значения в общую формулу корней, получим

1) если n=0, х = (- 1) 0 +0 = . Это число принадлежит заданному отрезку [0, ].

2) если n =1, х=(–1) 1 +== – + = . Это число принадлежит заданному отрезку [0, ].

3) если n =2, х =(- 1) 2 + = + = . Это число не принадлежит заданному отрезку [0, ]. Тем более не будут принадлежать заданному отрезку значения икс, которые получаются из общей формулы при n 2.

4) рассмотрим n = — 1, х =(- 1) — 1 — = – – = . Это число не принадлежит заданному отрезку [0, ], так как отрицательное. Тем более не будут принадлежать заданному отрезку значения икс, которые получаются из общей формулы при n 2 – 3у + 2 = 0. Корни этого уравнения 1 и 2.

Вернемся к переменной икс и получим два уравнения tg = 1 или tg = 2.

Так как уравнение tg x = a имеет решение для любого значения а и эти решения имеют вид х = arctg x a + πn, то для первого уравнения имеем: = arctg 1 + πn = + πn , значит, х = + 3πn(три пи на четыре плюс три пи эн).

Для второго уравнения имеем: =arctg2+πn , значит, х=3arctg2+3πn(сумма трех арктангенсов двух и трех пи эн).

Ответ: х = + 3πn, 3arctg2+3πn.

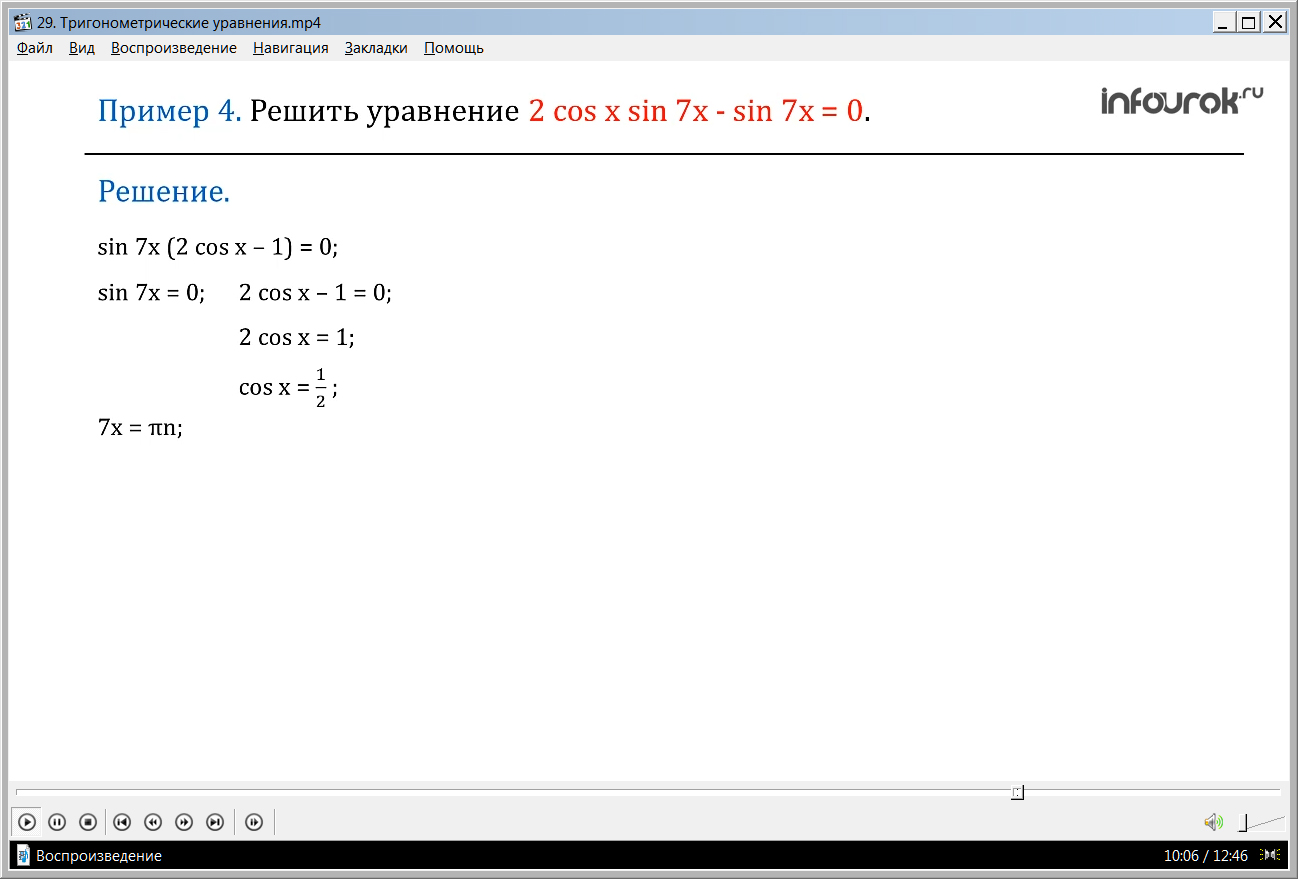
ПРИМЕР 4. Решить уравнение 2 cosхsin7x — sin 7x = 0.( два косинус икс на синус семи икс минус синус семи икс равно нулю)

Решение. Используем метод разложения на множители.

Вынесем за скобку sin 7x, получим sin 7x(2 cosх – 1) =0. Перейдем к совокупности уравнений:

Так как мы помним, что при а=0 х = πn,

то из первого уравнения находим, что 7х = πn, значит, х = .

Так как Решения уравнения cosx =a, при | а | 1, имеют вид:

х = arccosa + 2πn, а а=,

то из второго уравнения находим: х = arccos + 2πn,

А так как из определения арккосинуса числа а следует, что arccos это такое число, косинус которого равен

cos= , значит arccos = Подставив данное значение в найденное выражение х = arccos + 2πn, находим, что х = + 2πn.

ЗАМЕЧАНИЕ. При переходе от уравнения вида f₁(x) ∙ f₂(x) = 0 нужно быть очень внимательным.

Рассмотрим, например, уравнение ctgх(cosх – 1) =0.

1. Перейдем к совокупности уравнений:

Из уравнения ctg х= 0 находим по таблице значений котангенса: arcctg 0=, тогда х = + πn,

а из уравнения cos х =1 находим х .

Вспоминаем частные случаи:

Но включить в ответ второе решение нельзя, потому что при значениях х = 2πn множитель ctgх не имеет смысла, т.е. значения х = 2πn не принадлежат области определения уравнения (или по-другому области допустимых значений – ОДЗ). Значит х = 2πn — это посторонние корни.