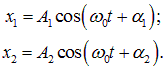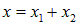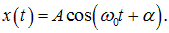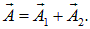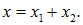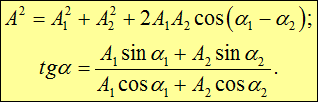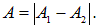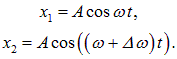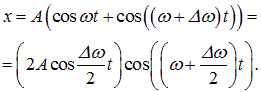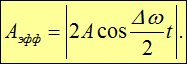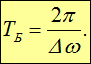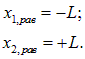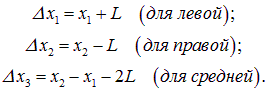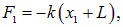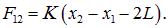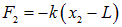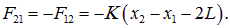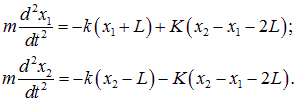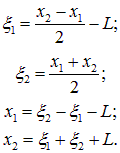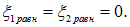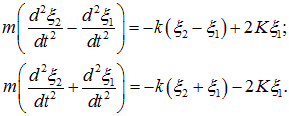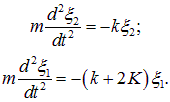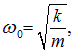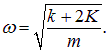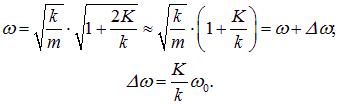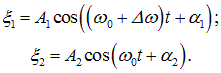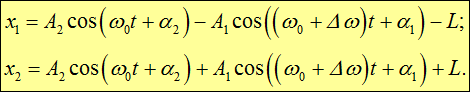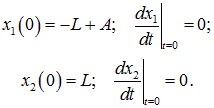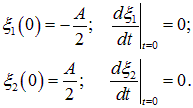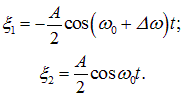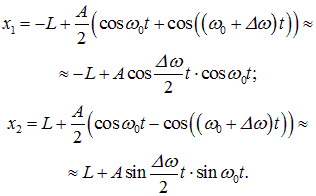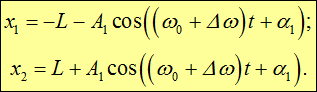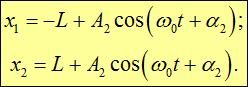При сложении одинаково направленных колебаний заданных уравнениями

При сложении одинаково направленных колебаний заданных уравнениями

КОЛЕБАНИЯ И ВОЛНЫ

Найти амплитуду А и начальную фазу φ₀ гармоничного колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями: X = 0,2 sіn (5t + π/2) и X = 0,03 sіn (5t + π//4).

Дано:

Решение:

Амплитуда результирующего колебания

Начальная фаза результирующего колебания

Ответ: ,

При сложении одинаково направленных колебаний заданных уравнениями

Вращение происходит против часовой стрелки, т. е. ω₀ > 0. За промежуток времени t вектор амплитуды повернется на угол rot и займет новое положение. Его проекция на опорную линию равна

Вращающийся вектор амплитуды полностью характеризует гармоническое колебание.

Проекция кругового движения на ось у также совершает гармоническое колебание y = A sin(ω₀t + φ). Таким образом, равномерное движение по окружности можно рассматривать как два колебательных гармонических движения, совершаемых одновременно в двух взаимно перпендикулярных направлениях. Этим представлением широко пользуются при сложении колебаний.

2.2.2. Сложение гармонических колебаний. Биения

Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль одной прямой.

Сложение колебаний будем проводить методом векторных диаграмм (рис. 2.2.2). Пусть колебания заданы уравнениями .

Рис. 2.2.2. Сложение гармонических колебаний одного направления x1 и х2) методом векторных диаграмм

Отложим из точки О вектор A1 под углом φ1 к опорной линии и вектор A2 под углом φ2. Оба вектора вращаются против часовой стрелки с одинаковой угловой скоростью ω, поэтому их разность фаз не

1.4. Сложение колебаний одного направления

Может случиться так, что осциллятор принимает участие в двух одинаково направленных колебаниях с разными амплитудами, частотами и начальными фазами. Рассмотрим сложение таких колебаний.

Сложение колебаний с одинаковыми частотами

Для простоты рассмотрим сначала случай, когда частоты складываемых колебаний одинаковы. Общие решения складываемых гармонических колебаний имеют вид:

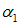
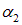
где x₁, x₂ — переменные, описывающие колебания, A₁, A₂ — их амплитуды, а , — начальные фазы. Результирующее колебание

удобно найти с помощью векторной диаграммы. Этот метод использует аналогию между вращением и колебательным процессом.

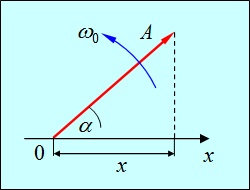
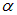
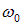
Возьмем общее решение (1.23) для гармонического колебания. Выберем ось 0x. Из точки 0 отложим вектор длиной A, образующий с осью 0x угол . Если привести этот вектор во вращение с угловой скоростью , то проекция конца этого вектора будет перемещаться по оси 0x от +A до –A, причем величина проекции будет изменяться по закону

Таким образом, проекция конца вектора на ось 0x будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени (рис. 1.12).

Рис. 1.12. Векторная диаграмма для общего решения (1.23)

Применим теперь эту технику к сложению колебаний (1.34). Представим оба колебания с помощью векторов А₁ и А₂ Возьмем их векторную сумму (рис. 1.13)

Рис. 1.13. Векторная диаграмма для сложения одинаково направленных колебаний одинаковой частоты

Проекция вектора А₁ на ось 0x равна сумме проекций соответствующих векторов

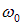
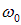
Таким образом, вектор А представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью , так что результирующее движение будет гармоническим колебанием с частотой , амплитудой A и начальной фазой a. Согласно теореме косинусов:

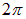
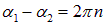
В частности, если фазы складываемых колебаний равны или отличаются на величину, кратную (то есть ), то амплитуда результирующего колебания равна сумме амплитуд

Если же складываемые колебания находятся в противофазе (то есть 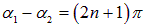), то

Биения

В этом разделе мы рассмотрим случай сложения одинаково направленных гармонических колебаний с разными частотами. На практике особый интерес представляет случай, когда складываемые колебания мало отличаются по частоте. Как мы увидим, в результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой, называемые биениями.

Биения — это периодическое изменение амплитуды колебаний, возникающее при сложении двух гармонических колебаний с близкими частотами.

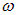
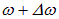
Для простоты рассмотрим случай, когда амплитуды складываемых колебаний равны A, а начальные фазы обоих колебаний равны нулю. Частоты складываемых колебаний равны, соответственно, и . Итак,

Складываем эти выражения и учитываем известную формулу тригонометрии:

Если 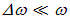то в аргументе второго косинуса мы можем пренебречь сдвигом частоты:

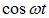
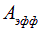
Кроме того, множитель в скобках меняется медленно по сравнению с . Поэтому результирующее колебание x можно рассматривать как модулированное гармоническое колебание с частотой w, эффективная амплитуда которого изменяется со временем по закону (1.40) (рис. 1.14):

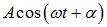
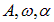
Подчеркнем, что в строгом смысле такое колебание не является гармоническим, и еще раз напомним, что, согласно определению, колебание гармоническое, если оно происходит по закону , причем все три его параметра: строго постоянны во времени.

Рис. 1.14. Биения при сложении колебаний с близкими частотами

Частота пульсаций амплитуды (ее называют частотой биений) равна разности частот складываемых колебаний. Период биений равен

Колебания двух связанных осцилляторов

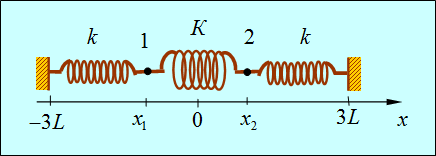
Приведем поучительный пример системы, в которой возникают биения. Рассмотрим два груза массой m, которые могут колебаться под действием двух одинаковых пружин с коэффициентами жесткости k. Пусть грузы соединены также мягкой пружиной с коэффициентом жесткости K<. Будем полагать длины всех пружин в нерастянутом состоянии одинаковыми и равными 2L (рис. 1.15).

Рис. 1.15. Пример связанных осцилляторов.
Колебания происходят вдоль оси 0х, сила тяжести не учитывается

Тогда в положении равновесия координаты грузов равны

При колебаниях координаты равны, соответственно, x₁(t), x₂(t). Удлинения пружин записываются как

Мы имеем дело с системой с двумя степенями свободы. Составим уравнения движения. На первый груз действуют сила со стороны пружины k, равная

и сила со стороны пружины K, равная

На второй груз действуют аналогичные силы

Соответственно, уравнения движения имеют вид

Эти уравнения не слишком похожи на первый взгляд на уравнения гармонических колебаний, потому что на колебания x₁ оказывают влияния колебания x₂ и наоборот. Поэтому преобразуем уравнения к новым переменным, уравнения для которых были бы независимыми (такие переменные называют нормальными координатами, а соответствующие им колебания — нормальными колебаниями (модами)). Именно, введем новые переменные x₁ и x₂:

Как легко убедиться, положениям равновесия соответствуют нулевые значения этих координат

В этих переменных уравнения (1.42) принимают вид:

Складывая и вычитая эти уравнения, приходим к паре независимых уравнений для введенных нормальных координат:

Первое уравнение описывает гармонические колебания с частотой

совпадающей с частотой колебаний пружинных маятников в отсутствие соединительной пружины К. Второе уравнение описывает колебания со сдвинутой частотой

Соответственно, мы получаем общее решение системы уравнений:

Общее решение для координат х₁ и х₂ колеблющихся точек следуют из (1.47) и (1.43):

Для примера рассмотрим случай, когда первая масса смещается на расстояние от положения равновесия и отпускается с нулевой начальной скоростью, а вторая масса остается в положении равновесия:

Этому соответствуют следующие начальные значения нормальных координат:

Такие начальные условия уже рассматривались выше. Соответствующие им решения имеют вид

Подставляя найденные амплитуды и начальные фазы в (1.48), получаем решения, описывающие колебания рассматриваемых масс около их положений равновесия:

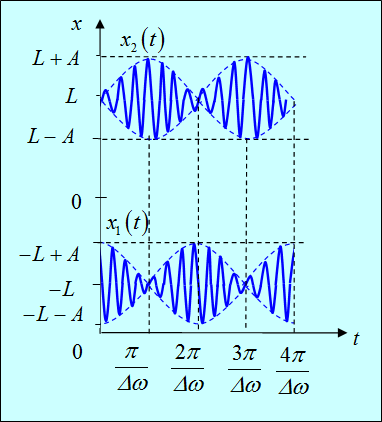
Графики функций x₁(t), x₂(t) показаны на рис. 1.16. Видна характерная картина биений.

Рис. 1.16. Биения в системе двух связанных осцилляторов

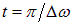
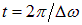
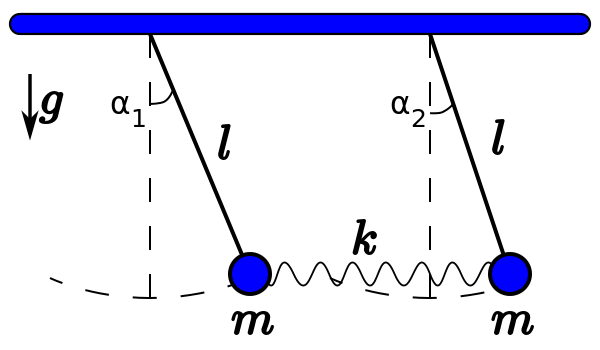
В начальный момент времени колеблется лишь первый груз. Затем начинает колебаться второй, а амплитуда колебаний первого уменьшается. Через время первый груз останавливается, а второй колеблется с максимально возможной амплитудой. Произошла «перекачка» энергии от первого маятника ко второму. Затем процесс «перекачки» энергии идет в обратном направлении и к моменту первый маятник колеблется с максимальной амплитудой, а второй покоится.

На рис. 1.17 демонстрируются биения в системе двух связанных математических маятников.

Рис. 1.17. Биения в системе связанных маятников

Выясним теперь физический смысл нормальных мод, соответствующих чисто гармоническим колебаниям системы. Если возбуждены колебания только первой из них (x₁), то A₂ = 0 и, как следует из общего решения (1.48),

Из (1.53) видно, что первая нормальная мода соответствует такому колебанию, когда оба груза смещаются на одинаковые расстояния от их положений равновесия, но в противоположные стороны, другими словами — они колеблются в противофазе. Скорости движения грузов также равны по величине и противоположны по направлению, так что центр масс грузов остается неподвижным. Колебания происходят под действием пружин с жесткостью k, к которым добавляется соединительная пружина с жесткостью К. Как следствие, частота таких колебаний больше частоты колебаний несвязанных осцилляторов

Возбуждение только второй (x₂) нормальной моды означает, что A₁ = 0:

В этом случае грузы смещаются из положения равновесия в одну сторону на одинаковые расстояния, другими словами – они колеблются синфазно. Скорости их также одинаковы по величине и направлению. Соединительная пружина колеблется вместе с грузами, но остается не растянутой и потому не оказывает влияния, так что частота колебаний совпадает с частотой колебаний несвязанных маятников.

В разобранном случае мы познакомились с нормальными модами и выяснили, что их частоты сдвигаются по сравнению с частотами колебаний несвязанных маятников. Любое другое колебательное движение системы можно представить как суперпозицию нормальных мод. Аналогичным образом можно рассмотреть цепочку из множества связанных друг с другом осцилляторов и изучить их нормальные колебания. Такая система представляет собой модель кристаллической решетки.