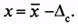Совокупные измерения
Совокупные измерения – измерения, в которых значения нескольких одновременно измеряемых однородных величин находят решением системы уравнений, которые связывают разные комбинации этих величин, измеряемые прямо или косвенно.
Систему уравнений совокупных измерений можно записать в следующем виде

где i=1,2,…, n; n>m. То есть характерной особенностью совокупных измерений, также как и совместных, является то обстоятельство, что число уравнений больше, чем число неизвестных.
Здесь 
Таким образом, в отличие от косвенных измерений, производятся измерения нескольких искомых величин, причем последние находятся в результате решения системы уравнений.
Легко заметить, что система уравнений (3.53) аналогична системе уравнений совместных измерений. Имеется, однако, принципиальное отличие совокупных измерений от совместных, прежде всего в постановке измерительной задачи: в результате совокупных измерений определяется не функциональная зависимость между величинами (как это делается при совместных измерениях), а сами величины, причем величины одноименные.
Несмотря на отличия, обработка экспериментальных данных при совместных и совокупных измерениях, производится практически одними и теми же приемами.
Классическим примером совокупных измерений является измерение емкости двух конденсаторов С1 и С2 по результатам измерения емкости каждого из них в отдельности, а также при параллельном и последовательном их соединении. Такой метод применяется для уменьшения систематической погрешности измерения, различной в разных точках диапазона измерения.
В этом случае, хотя каждое измерение выполняется с одним наблюдением, но в итоге для двух неизвестных будем иметь систему из четырех уравнений

Последнее уравнение системы – нелинейное, поэтому применим для этой системы метод линеаризации, рассмотренный для случая совместных измерений, и заключающийся в разложении всех уравнений системы в ряд Тейлора. В этом случае получаем следующие значения частных производных
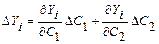


используя которые можно записать исходную систему линейных уравнений

Для решения этой системы необходимо выбрать точки разложения 


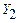
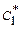

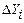

Подставляя эти невязки в уравнение (3.55), можно получить из нее систему нормальных уравнений (по МНК)

Решая систему, получаем 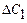

искомые 

Совокупные измерения широко распространены в метрологической практике, например, при калибровке мер или шкал приборов. В этом случае система уравнений совокупных измерений имеет вид

где 


m — количество значений величин, подлежащих определению;
n — количество комбинаций (уравнений).
При калибровке коэффициенты 
0 – если 
1 – если измеряется сумма нескольких величин, в которую входит 
-1 – если сумма нескольких величин сравнивается с 
Если число уравнений равно числу неизвестных, то система (3.57) решается однозначно, а действительные значения измеряемых величин и доверительные интервалы их погрешностей определяются методами обработки косвенных измерений. Однако, для уменьшения погрешностей калибровки производится сравнение большего числа комбинаций, чем количество определяемых значений величин. Тогда оценивание результатов измерений производится как при совместных измерениях. Для решения системы условных уравнений обычно применяют МНК. Этот метод, как уже было сказано, вытекает из принципа максимального правдоподобия и является оптимальным при следующих условиях:
— результаты измерения Y содержат независимые случайные погрешности с нулевыми математическими ожиданиями и одинаковыми дисперсиями;
— погрешности имеют нормальное распределение.
При выполнении этих условий получаемые оценки будут состоятельными, несмещенными и эффективными.
Аналогично рассмотренному в разделе 3.4, можно записать систему уравнений относительно невязок

Сумма их квадратов будет равна

Дифференцируя выражение (3.59) по параметрам 

преобразуя которую и применяя обозначение Гаусса, получаем нормальную систему уравнений относительно 

Решение этой системы с помощью определителей имеет вид

где D – главный определитель системы

а определитель 

Оценки СКО 

где 

Невязки 
Границы погрешности совокупных измерений определяют из выражения

где ts– коэффициент Стьюдента для (n-m) степеней свободы.
Примером совокупных измерений являются проводимые при калибровке набора из пяти гирь массой m1 = 5 кг, m2 = 2 кг, m3 = 2 кг, m4 = 1кг, m5 = 1кг по образцовой гире массой m0 = 10кг. В этом случае можно получить следующую систему из десяти уравнений:


Невязки di для этих уравнений получают, проводя сравнения гирь в перечисленных сочетаниях с помощью равноплечих весов, имеющих шкалу для отсчета разности масс.
Обработка результатов полученных совместных измерений осуществляется по формуле (3.63) — (3.67).
Контрольные вопросы, задачи, упражнения
1. Перечислите основные этапы измерений и их содержание.
2. Какие измерения называются прямыми? Каков физический смысл коэффициентов, входящих в уравнение прямых измерений?
3. Изложите порядок обработки прямых измерений с однократными наблюдениями.
4. Какова цель проведения прямых измерений с многократными наблюдениями? Какие задачи решаются в процессе достижения этой цели.
5. Изложите порядок обработки прямых измерений многократными наблюдениями.
6. Как производится суммирование систематических и случайных погрешностей при прямых измерениях?
7. Изложите порядок определения границ случайной погрешности при проведении прямых измерений с многократными наблюдениями.
8. Какие условия должны выполняться для обеспечения статистической однородности групп наблюдений?
9. Определите однородность и равнорассеянность двух групп наблюдений величины x и возможность их объединения. Рассчитайте оценки математического ожидания и СКО объединённых результатов наблюдений для доверительной вероятности 0,95.
| x1 | 2.606 | 2.419 | 2.117 | 1.814 | 1.627 |
| x2 | 1.52 | 1.581 | 1.797 | 2.128 | 2.491 |
| x1 | 1.627 | 1.813 | 2.115 | 2.418 | 2.606 |
| x2 | 2.788 | 2.934 | 2.881 | 2.642 | 2.283 |
10. Пользуясь принципом максимального правдоподобия, найдите эффективные оценки математического и дисперсии объединённых групп неравноточных наблюдений, если средние арифметические в группах распределены по нормальному закону.
11. Какие измерения называют косвенными? Как, имея уравнение косвенного измерения, записать выражение для его абсолютной погрешности?
12. Определите относительную методическую погрешность косвенного измерения напряжения на двух последовательно соединенных резисторах 10 кОм и 20 кОм по результатам измерения напряжения на каждом из них, если внутреннее сопротивление вольтметра составляет 100 кОм.
13. Результаты измерения напряжения U на двух последовательно соединенных резисторах определены посредством косвенных измерений на каждом из них. Значение U1 и U2 в одни и те же моменты времени приведены в таблице.
| U1 | 106.6 | 105.6 | 104.4 | 103.4 |
| U2 | 207.5 | 208.7 | 208.9 | 206.3 |
| U1 | 103.0 | 103.4 | 105.6 | 106.8 |
| U2 | 204.5 | 203.3 | 205.7 | 207.5 |
Определите значение оценки дисперсии результатов наблюдений 
14. Изложите алгоритм обработки результатов измерений с многократными наблюдениями аргументов.
15. В чем суть критерия ничтожных погрешностей и для чего он используется?
16. С помощью МНК определите параметра А и В зависимости 
 | ||||||
 | 9,2 | 10,4 | 11,7 | 12,9 | 14,2 | 15,4 |
 | 13,37 | 10,72 | 8,95 | 7,68 | 6,72 | 5,98 |
 | 0,38 | 0,92 | 1,51 | 2,15 | 2,84 | |
 | 21,68 | 12,71 | 9,72 | 8,23 | 7,33 | |
 | 0,2292 | 0,2841 | 0,3848 | 0,3228 | 0,3319 | |
 | 19,35 | 32,68 | 40,48 | 46,02 | 50,31 | |
 | 7,84 | 8,45 | 9,1 | 9,81 | 10,57 | 11,39 |
 | |||||
 | 16,7 | 17,9 | 19,2 | 20,4 | |
 | 5,39 | 4,9 | 4,49 | 4,15 | |
 | 3,55 | 4,3 | 5,03 | 5,87 | 6,69 |
 | 6,73 | 6,3 | 5,98 | 5,73 | 5,53 |
 | 0,3882 | 0,3488 | 0,3464 | 0,3493 | 0,3516 |
 | 53,82 | 56,78 | 59,35 | 61,62 | 63,64 |
 | 12,26 | 13,23 | 14,26 | 15,37 | 16,57 |
17. Приведите выражения для определения коэффициента корреляции. В каких пределах он изменяется? Что определяет?
18. Как производится проверка на допустимость линеаризации искомой величины от аргументов?
19. Почему уравнения исходной избыточной системы при совместных и совокупных измерениях называются условными?
20. Каковы условия применимости МНК?
21. Где в метрологической практике применяются совместные и совокупные измерения?
22. Изложите суть МНК.
23. Объясните основные методы линеаризации при определении параметров неполиномиальных зависимостей с помощью МНК.
Классификация видов измерений
Измерения различают по способу получения информации, по характеру изменений измеряемой величины в процессе измерений, по количеству измерительной информации, по отношению к основным единицам.
По способу получения информации измерения разделяют на прямые, косвенные, совокупные и совместные.
Прямые измерения – это непосредственное сравнение физической величины с ее мерой. Например, при определении длины предмета линейкой происходит сравнение искомой величины (количественного выражения значения длины) с мерой, т. е. линейкой.
Косвенные измерения – отличаются от прямых тем, что искомое значение величины устанавливают по результатам прямых измерений таких величин, которые связаны с искомой определенной зависимостью. Так, если измерить силу тока амперметром, а напряжение вольтметром, то по известной функциональной взаимосвязи всех трех величин можно рассчитать мощность электрической цепи.
Совокупные измерения – сопряжены с решением системы уравнений, составляемых по результатам одновременных измерений нескольких однородных величин. Решение системы уравнений дает возможность вычислить искомую величину.
Совместные измерения – это измерения двух или более неоднородных физических величин для определения зависимости между ними.
Совокупные и совместные измерения часто применяют в измерениях различных параметров и характеристик в области электротехники.
По характеру изменения измеряемой величины в процессе измерений бывают статистические, динамические и статические измерения.
Статистические измерения связаны с определением характеристик случайных процессов, звуковых сигналов, уровня шумов и т. д. Статические измерения имеют место тогда, когда измеряемая величина практически постоянна.
Динамические измерения связаны с такими величинами, которые в процессе измерений претерпевают те или иные изменения. Статические и динамические измерения в идеальном виде на практике редки.
По количеству измерительной информации различают однократные и многократные измерения.
Однократные измерения – это одно измерение одной величины, т. е. число измерений равно числу измеряемых величин. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями, поэтому следует проводить не менее трех однократных измерений и находить конечный результат как среднее арифметическое значение.
Многократные измерения характеризуются превышением числа измерений количества измеряемых величин. Преимущество многократных измерений – в значительном снижении влияний случайных факторов на погрешность измерения.
По используемому методу измерения – совокупности приемов использования принципов и средств измерений различают:
- метод непосредственной оценки;
- метод сравнения с мерой;
- метод противопоставления;
- метод дифференциальный;
- метод нулевой;
- метод замещения;
- метод совпадений.
По условиям, определяющим точность результата, измерения делятся на три класса: измерения максимально возможной точности, достижимой при существующем уровнетехники; контрольно-поверочные измерения, погрешность которых не должна превышать некоторое заданное значение; технические (рабочие) измерения, в которых погрешность результата измерения определяется характеристиками средств измерений.
по общим приемам получения результатов измерений — прямые, косвенные, совместные, совокупные.
Классификация измерений.
Цель измерения — получение значения величины в форме, наиболее удобной для пользования. С помощью измерительного прибора сравнивают размер величины, информация о котором преобразуется в перемещение указателя, с единицей, хранимой шкалой этого прибора.
Измерения весьма разнообразны и классифицировать их можно по различным признакам. В настоящее время принята следующая классификация:
по характеристике точности — равноточные, неравноточные;
по числу измерений в серии — однократные и многократные;
по отношению к изменению измеряемой величины — статические и динамические;
по метрологическому назначению — технические и метрологические;
по выражению результата измерений — абсолютные и относительные;
по общим приемам получения результатов измерений — прямые, косвенные, совместные, совокупные.
Равноточные измерения — ряд измерений какой-либо величины, выполняемых одинаковыми по точности средствами измерений в одних и тех же условиях. Если одно из этих условий не выполняется, то измерения называют неравноточными.
Однократное измерение — измерение, выполняемое один раз. Например, определение времени по часам. Если необходима большая уверенность в получаемом результате, то проводятся многократные измерения, результат которых получают из нескольких следующих друг за другом измерений. За результат многократного измерения обычно принимают среднее арифметическое значение из результатов однократных измерений, входящих в ряд.
Статическое измерение — измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения. Например, измерение длины детали при нормальной температуре. Если размер физической величины изменяется с течением времени, то такие измерения называют динамическими. Примером таких измерений может быть определение расстояния до поверхности земли со снижающегося самолета.
Технические измерения обычно используются в ходе контроля при изготовлении изделий, технологических процессов. Например, измерение давления пара в котле при помощи манометра. Обычно они выполняются с помощью рабочих средств измерений.
Метрологические измерения предназначаются для воспроизведения единиц физических величин или для передачи их размера рабочим средствам измерений. В ходе их выполнения используются эталоны или образцовые средства измерений.

Абсолютное измерение — измерение, приводящее к значению измеряемой величины, выраженному в ее единицах. При измерении длины детали штангенциркулем результат выражается в единицах измеряемых величин (в миллиметрах).
В относительных измерениях измеряется отношение величины к одноименной величине, играющей роль единицы или измерения величины по отношению к одноименной величине, принимаемой за исходную. Примером может служить измеритель скорости у сверхзвуковых самолетов, показывающий отношение скорости самолета к скорости звука или указатели расхода бензина в автомобилях.
Подробнее рассмотрим прямые, косвенные, совместные и совокупные измерения.
К прямым относятся измерения, результаты которых получают с помощью средств измерений, находящихся под воздействием данной измеряемой величины, проградуированной непосредственно в единицах этой величины. При проведении этих измерений, как правило, не требуется проведения каких-либо вычислений.
Математически прямое измерение может быть представлено в виде уже приводившейся формулы (1.1) Числовое значение X, характеризующее разряд величины Q выраженной в единицах [Q], определяется непосредственно по показаниям мер или измерительных приборов, предназначенных для измерений данной величины Q.
Примером прямых измерений могут быть измерения длины линейкой, времени при помощи часов, массы при помощи гирь на равноплечих весах, температуры — термометром, силы тока — амперметром и т. д.
Прямое измерение может также заключаться в однократном применении измерительного прибора с непосредственным отсчетом по нему результата, но может включать и несколько повторных наблюдений с вычислением результата как среднего из нескольких измерений. Для получения результата также может потребоваться умножение отсчета по шкале измерительного прибора на цену деления.
Косвенныминазывают измерения, при которых искомое значение величины находят на основании известной зависимости между этой величиной и величинами, определяемыми прямыми измерениями. Результат находят из решения уравнения, выражающего эту зависимость. Косвенное измерение можно описать уравнением
где Q — измеряемая величина; X, Y, Z…W — величины, размер которых определяется из прямых измерений. В этом уравнении (X, У, Z. ) представляют конкретные реализации величин, связанных с некоторым определенным объектом. Рассмотрим пример. Требуется измерить удельное электрическое сопротивление некоторого материала. Но так как приборов для прямых измерений удельного сопротивления нет, его можно измерить только косвенным методом.
Совокупными измерениями называют одновременные измерения нескольких одноименных величин, при которых искомое значение находят решением системы уравнений, получаемых в результате прямых измерений различных сочетаний этих величин.
Совместными называют производимые одновременно (прямые и косвенные) измерения двух и более разноименных величин. Целью таких измерений является, фактически, определение функциональной связи между величинами.
В метрологии, использующей теорию вероятностей, основными величинами являются отдельные значения случайных величин, а производными — мера их рассеивания (дисперсия) и др.
Понятие о методах измерений.Метод измерений — прием или совокупность приемов сравнения измеряемой величины с ее единицей в соответствии с реализованным принципом измерений.
Методы измерений классифицируют по нескольким признакам. По общим приемам получения результатов измерений различают: 1) прямой метод измерений; 2) косвенный метод измерений. Первый реализуется при прямом измерении, второй — при косвенном измерении, которые описаны выше.
По условиям измерения различают контактный и бесконтактный методы измерений.
Контактный метод измерений основан на том, что чувствительный элемент прибора приводится в контакт с объектом измерения (измерение температуры тела термометром). Бесконтактный метод измерений основан на том, что чувствительный элемент прибора не приводится в контакт с объектом измерения (измерение расстояния до объекта радиолокатором, измерение температуры в доменной печи пирометром).
Исходя из способа сравнения измеряемой величины с ее единицей, различают методы непосредственной оценки и метод сравнения с мерой.
При методе непосредственной оценки определяют значение величины непосредственно по отсчетному устройству показывающего СИ (термометр, вольтметр и пр.). Мера, отражающая единицу измерения, в измерении не участвует. Ее роль играет в СИ шкала, проградуированная при его производстве с помощью достаточно точных СИ.

Загрузка.
При методе сравнения с мерой измеряемую величину сравнивают с величиной, воспроизводимой мерой (измерение массы на рычажных весах с уравновешиванием гирями). Существует ряд разновидностей этого метода: нулевой метод, метод измерений с замещением, метод совпадений.
Вынесенные в заголовок учебного вопроса понятия призваны характеризовать качество измерений.
Под качеством измерений понимают совокупность свойств, обусловливающих получение результатов с требуемыми точностными характеристиками, в необходимом виде и в установленные сроки. Качество измерений характеризуется такими показателями, как точность, правильность и достоверность. Эти показатели должны определяться по оценкам, к которым предъявляются требования состоятельности, несмещенности и эффективности.
Истинное значение измеряемой величины отличается от среднего значения на величину систематической погрешности 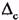
Если систематическая составляющая исключена, то 
Оценку x числовой характеристики закона распределения х изображаемую точкой на числовой оси, называют точечной оценкой. В отличие от числовых характеристик оценки являются случайными величинами. Причем их значение зависит от числа наблюдений п.
Состоятельной называют оценку, которая сводится по вероятности к оцениваемой величине, т.е.
Несмещенной является оценка, математическое ожидание которой равно оцениваемой величине, т.е.
Эффективной называют такую оценку, которая имеет наименьшую дисперсию
Перечисленным требованиям удовлетворяет среднее арифметическое х результатов п наблюдений.
Таким образом, результат отдельного измерения является случайной величиной. Тогда точность измерений — это близость результатов измерений к истинному значению измеряемой величины.
Если систематические составляющие погрешности исключены, то точность результата измерений Зσ характеризуется степенью рассеяния его значения, т. е. дисперсией. Как показано выше (см. формулу 2.4), дисперсия среднего арифметического а* в п раз меньше дисперсии отдельного результата наблюдения.
На рис. 2.9 заштрихованная площадь относится к плотности вероятности распределения среднего значения.
Рис. 2.9. Плотность распределения отдельного и суммарного результата измерения
Правильность измерений определяется близостью к нулю систематической погрешности.
Достоверность измерений зависит от степени доверия к результату и характеризуется вероятностью того, что истинное значение измеряемой величины лежит в указанных окрестностях действительного.
Следует отметить, что результаты измерений, не обладающие достоверностью, т. е. степенью уверенности в их правильности не представляют ценности. Например, датчик измерительной схемы может иметь весьма высокие метрологические характеристики, но влияние погрешностей от его установки, внешних условий, методов регистрации и обработки сигналов приведет к большой конечной погрешности измерений.
Наряду с такими показателями, как точность, достоверность и правильность, качество измерительных операций характеризуется также сходимостью и воспроизводимостью результатов. Эти показатели наиболее распространены при оценке качества испытаний и характеризуют точность испытаний.
Очевидно, что два испытания одного и того же объекта одинаковым методом не дают идентичных результатов. Объективной мерой их могут служить статистически обоснованные оценки ожидаемой близости двух или более числа результатов, полученных при строгом соблюдении методики испытаний. В качестве таких статистических оценок согласованности результатов испытаний принимаются сходимость и воспроизводимость.
Сходимость (повторяемость) — это близость результатов двух испытаний, полученных одним методом, на идентичных установках, в одной лаборатории. Воспроизводимость отличается от сходимости тем, что оба результата должны быть получены в разных лабораториях. При доверительной вероятности Р= 0,95 сходимость определяется как r=2,77σсх , а воспроизводимость — R = 2,77σв.
Здесь σсх и σв — стандартные отклонения результатов испытаний соответственно в условиях сходимости и воспроизводимости:
где х1 и х2 — результаты единичных испытаний в условиях сходимости; у1 и у2 — результаты единичных испытаний в условиях воспроизводимости; 
Отдельные стандарты задают значения r и R.
Прецизионность зависит только от случайных погрешностей и не имеет отношения к истинному или опорному значению измеряемой величины. Меру прецизионности обычно выражают в терминах неточности и вычисляют как стандартное отклонение результатов измерений. Меньшая прецизионность соответствует большему стандартному отклонению. Количественные значения мер прецизионности существенно зависят от регламентированных условий. Крайними случаями таких условий являются условия повторяемости и условия воспроизводимости.
Повторяемость — прецизионность в условиях повторяемости. В отечественных НД наряду с термином «повторяемость» используют термин «сходимость».
Условия повторяемости (сходимости) — условия, при которых независимые результаты измерений (или испытаний) получаются одним и тем же методом на идентичных объектах испытаний, в одной и той же лаборатории, одним и тем же оператором, с использованием одного и того же оборудования, в пределах короткого промежутка времени. В качестве мер повторяемости (а также воспроизводимости) в Стандарте 5725 используются стандартные отклонения.
http://be5.biz/ekonomika/m012/42.html
http://poisk-ru.ru/s5125t2.html