Приближения использующиеся для решения уравнения шредингера

Решение уравнения Шредингера для многоэлектронных атомов

Автор работы: Пользователь скрыл имя, 13 Октября 2013 в 00:54, реферат

Краткое описание

Уравнение Шрёдингера для атомов, содержащих более одного электрона, не может быть решено в аналитическом виде. В связи с этим рассматривают приближённые методы, наиболее существенным, из которых является метод самосогласованного поля. Идея метода заключается в том, что каждый электрон в атоме рассматривается как движущийся в самосогласованном поле, создаваемом ядром вместе со всеми остальными электронами.

Содержание

Введение…………………………………………………………………………….3
Многоэлектронные атомы…………………………………………………………4
Методы решения уравнения Шредингера для многоэлектронных атомов
1.1 . Метод самосогласованного поля Хартри…………………………………. 5
1.2. Принцип Паули и определители Слейтора. Метод Хартри – Фока………7
Вывод………………………………………………………………………………10
Литература………………………………………………………………………. 11

Прикрепленные файлы: 1 файл

сдать2.doc

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

РЕШЕНИЕ УРАВНЕНИЯ ШРЕДЕНГЕРА ДЛЯ МНОГОЭЛЕКТРОННЫХ АТОМОВ

Выполнила студентка 4 курса 2 группы естественно-географического

факультета отделения «Химия-биология»

Проверила доцент кафедры химии

Методы решения уравнения Шредингера для многоэлектронных атомов

1.2. Принцип Паули и определители Слейтора. Метод Хартри – Фока………7

Введение.

Построение самосогласованного поля может осуществляться либо методом последовательных приближений (изначально предложенным Хартри) или прямым вариационным методом.

Существенно, что вычисления методом самосогласованного поля весьма громоздки, особенно для сложных атомов. Для них применяется другой метод — метод Томаса — Ферми.

Обобщение метода Хартри — Фока, в котором учитываются волновые функции пар частиц, является метод Хартри — Фока — Боголюбова.

В атоме водорода электрон находится в силовом поле, которое создается только ядром. В многоэлектронных атомах на каждый электрон действует не только ядро, но и все остальные электроны. При этом электронные облака отдельных электронов как бы сливаются в одно общее многоэлектронное облако. Точное решение уравнения Шредингера для таких сложных систем связано с большими затруднениями и, как правило, недостижимо. Поэтому состояние электронов в сложных атомах и в молекулах определяют путем приближенного решения уравнения Шредингера.

Общим для всех приближенных методов решения этого уравнения является так называемое одноэлектронное приближение, т. е. предположение, что волновая функция многоэлектронной системы может быть представлена в виде суммы волновых функций отдельных электронов. Тогда уравнение Шредингера может решаться отдельно для каждого находящегося в атоме электрона, состояние которого, как и в атоме водорода, будет определяться значениями квантовых чисел n, l, m и s. Однако и при этом упрощении решение уравнения Шредингера для многоэлектронных атомов и молекул представляет весьма сложную задачу и требует большого объема трудоемких вычислений. В последние годы подобные вычисления выполняются, как правило, с помощью быстродействующих электронных вычислительных машин, что позволило произвести необходимые расчеты для атомов всех элементов и для многих молекул.

Исследование спектров многоэлектронных атомов показало, что здесь энергетическое состояние электронов зависит не только от главного квантового числа n, но и от орбитального квантового числа l. Это связано с тем, что электрон в атоме не только притягивается ядром, но и испытывает отталкивание со стороны электронов, расположенных между данным электроном и ядром. Внутренние электронные слои как бы образуют своеобразный экран, ослабляющий притяжение электрона к ядру, или, как принято говорить, экранируют внешний электрон от ядерного заряда. При этом для электронов, различающихся значением орбитального квантового числа l, экранирование оказывается неодинаковым.

В многоэлектронных атомах энергия электрона зависит не только от главного, но и от орбитального квантового числа. Главное квантовое число определяет здесь лишь некоторую энергетическую зону, в пределах которой точное значение энергии электрона определяется величиной l. В результате возрастание энергии по энергетическим подуровням происходит примерно в следующем порядке:

ls 2 \r_ij в уравнении , зависящей от координат двух электронов, выражающим, описывающим межэлектронного взаимодействия как функцию координат каждого отдельного электрона: V_эф.

Чтобы определить особые функции ѱ_i и особые значения оператора гамильтона надо знать потенциал V_эф.( ѱ_i), который зависит от искомых функций. Эта трудность устраняется в методе последовательных приближений. В качестве начальных волновых функций берут какие-либо пробные функции, например, функции водородоподобного атома.

Затем решают уравнение Шредингера и находят функции первого приближения усредненного потенциала. Обычно новые величины энергий межэлектронного взаимодействия сильно отличается от первоначальных, что связано с неточностью исходных функций. Поэтому находят функции следующего приближения и т.д.

Критерием получения достаточно хороших ѱ_i является совпадение с заданной точностью величин V_эф., рассчитанных для ѱ n и ѱ (n+1) т.е. потенциалы V_эф. должны быть согласованными с функциями ѱ_i . Это требование и определяет название метода самосогласованного поля.

Уравнение Шрёдингера

Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.

Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.

Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.

Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу — в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное — примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):

где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.

Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.

Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера — Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий — то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.

Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).

Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.

Уравнение Шредингера для кристалла

Возможные значения энергии электрона в кристалле можно найти из решения уравнения Шредингера для стационарных состояний, которое в общем случае имеет вид:

HY = EY, (1.31)

где H – оператор Гамильтона для кристалла, E – полная энергия кристалла, Y — волновая функция кристалла.

Волновая функция Ψ(x,t) обычно определяется из выражения для плотности вероятности нахождения частицы в точке x в момент времени t.

В общем случае волновая функция является комплексной величиной и имеет следующий вид:

(1.32)

Так как вероятность должна быть величиной действительной, то для нахождения плотности вероятности необходимо умножить Ψ(x,t) на комплексно сопряженную с ней функцию Ψ * (x,t). Комплексно-сопряженная волновая функция:

(1.33)

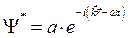
Квадрат амплитуды волновой функции характеризует вероятность (P) нахождения электрона в данной точке пространства, определяемой радиус-вектором .

(1.34)

или более точно:

Квадрат модуля волновой функции, умноженный на элемент объема есть вероятность обнаружить электрон в момент времени t в объеме , образующий бесконечно малую окрестность точки .

Уравнение Шредингера должно быть дополнено ограничениями, накладываемыми на волновую функцию:

— волновая функция должна быть конечной (так как вероятность не может быть больше 1), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).

— производные ¶Y/¶x, ¶Y/¶y, ¶Y/¶z должны быть непрерывны

— функция |Y| 2 должна быть интегрируема. Это условие в простейших случаях сводится к условию нормировки вероятности (т.к. электрон имеется, вероятность его существования где-то в пространстве — 100%-ная):

(1.40)

Рис. 1.40. Плотность вероятности нахождения электрона в пространстве.

Твердое тело представляет собой единую систему легких (электронов) и тяжелых (ядра) частиц. Наиболее полные сведения о свойствах такой системы, в том числе и об ее энергетическом спектре, можно получить решая уравнение Шредингера, соответствующее стационарным состояниям этой системы. Но, из-за того, что в кристалле имеет место большое число взаимодействий, уравнение Шредингера приобретает сложный вид:

(1.41)

В уравнение (2.3) входят следующие виды энергии:

1) Кинетическая энергия электронов: , где -постоянная Дирака ( = h/2 ), m-масса электрона, а — оператор Лапласа для i-го электрона;

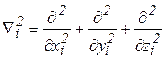
2) Кинетическая энергия ядер: , где -масса ядра;

3) Потенциальная энергия попарного взаимодействия электронов между собой: 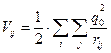, где -заряд электрона, здесь i ≠ j(!)

4) Потенциальная энергия попарного взаимодействия ядер между собой:

5) Потенциальная энергия взаимодействия электронов с ядрами: ,

где — координаты электронов и ядер соответственно;

6) Полная энергия кристалла E .

— собственная волновая функция кристалла, зависящая от координат всех электронов и атомных ядер.

Уравнение (21) содержит 3N(Z+1) независимых переменных, где N – число атомов в кристалле, Zq₀ – заряд ядра. Число атомов в 1 см 3 составляет примерно 5*10 22 и каждый атом содержит большое число электронов. Следовательно, волновая функция зависит от огромного числа (10 24 -10 25 ) независимых переменных (в кремнии: 3N(Z+1) = 3 · 5х10 22 · (14+1) = 2.25х10 24 переменных). Точное решение уравнения Шредингера невозможно даже для отдельных атомов, за исключением атома водорода. Поэтому задача сводится к нахождению приближений в рамках физически оправданных упрощающих предположений. Зонная теория, лежащая в основе современной физики полупроводников, базируется на следующих основных приближениях:

(а) Адиабатическое приближение (приближение Борна — Оппенгеймера)

В его основе лежит тот факт, что масса ядер много больше, чем масса электронов (даже если бы кристалл состоял из самых легких атомов – атомов водорода, то M = m_p = 1836 m_e). В равновесном состоянии средние значения кинетической энергии тех и других частиц одного порядка. Поэтому скорости движения электронов намного превосходят скорости ядер (для кремния, скорость электронов V_e превышает скорость ядра V_я в

230 раз). При каждом изменении положения ядер практически мгновенно устанавливается пространственное распределение электронов, соответствующее новому положению ядер. Это позволяет в первом приближении рассматривать движение электронов в потенциальном поле фиксированных ядер. При изучении движения ядер, напротив, следует учитывать не мгновенное положение электронов, а поле, создаваемое их средним пространственным распределением.

Таким образом суть адиабатического приближения состоит в том, что движение электронов и ядер можно считать независимым, происходящим без обмена энергией между электронной и ядерной подсистемами частиц.

Следствия:

а) Так как электронная и ядерная подсистемы независимы, то волновую функцию Y, как следует из теории вероятности, можно представить в виде произведения электронной Y_e и ядерной волновых функций:

(1.42)

б) Если допустить, что ядра покоятся, тогда кинетическая энергия ядер обращается в нуль.

в) Энергия взаимодействия электронов и ядер V_о принимает постоянное значение. Выбором начала отсчета энергии V_о можно обратить в нуль. Подстановка (1.42) в уравнение Шредингера (1.41) позволяет разделить уравнения Шредингера для ядер и для электронов и получить уравнение для электронов в виде:

(1.43)

где — координаты покоящихся ядер, E, — соответственно энергия и волновая функция электронов.

(б) Валентная аппроксимация.

Поскольку состояние внутренних атомных электронов мало изменяется в кристаллической решетке, то можно ограничиться рассмотрением только валентных электронов, а под подразумевать координаты не ядер, а атомных остатков. При этом уравнение (1.43) записывают только для валентных электронов, движущихся в потенциальном поле фиксированных атомных остатков.

Несмотря на проведенные упрощения, уравнение (1.43) не может быть решено в общем виде, так как по-прежнему имеем дело с многоэлектронной задачей. Чтобы свести многоэлектронную задачу к одноэлектронной, для этого сделаем ещё одно допущение.

(в) Одноэлектронное приближение (метод Хартри-Фока)

Его суть заключается в том, что энергию попарного взаимодействия электронов заменяют энергией взаимодействия каждого электрона с усредненным полем всех остальных электронов. Это поле получило название самосогласованного, так как оно не только определяет движение данного электрона, но и само зависит от его движения. Введение самосогласованного поля позволяет рассматривать электроны в кристалле как невзаимодействующие частицы, т.е. движущиеся независимо друг от друга. Это является основанием для представления электронов проводимости в виде идеального газа и в уравнении (1.43) двойную сумму заменить суммой а -суммой ,

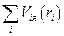
где — потенциальная энергия i-го электрона в поле всех остальных электронов, — потенциальная энергия i-го электрона в поле всех ядер.

После такой замены уравнение (1.43) распадается на сумму п одинаковых для всех электронов индивидуальных одноэлектронных уравнений вида

, (1.44)

где и Е— соответственно волновая функция и энергия электрона в кристалле.

Обозначив потенциальную энергию электрона в кристалле через функциюравную

(1.45)

уравнение (1.44) можно записать так:

,(1.46)

а для одномерного случая:

. (1.47)

Таким образом, в результате обоих приближений удалось свести задачу к обычному по форме уравнению Шредингера, но с другой функцией. В изолированном атоме, как известно, потенциальная фунция имеет вид гиперболы (см. рис. 1.38 и 1.41 (а)). В кристалле, соответственно, будет чередующийся ход таких гипербол, схематично изображенный на рис. 1.41. Обратите внимание, что наличие химических связей приводит к суперпозиции потенциалов, что сопровождается уменьшением средней амплитуды потенциального рельефа (рис. 1.41 (б) и (в))

Существуют различные способы рационального выбора вида функции V(r) для решения одноэлектронной задачи. Наиболее часто для этого используются состояние электрона, находящегося в потенциальном поле всех ионов решетки, заряд которых в среднем скомпенсирован зарядом валентных электронов.

Рис.1.41.Схематическое изображение потенциала одного атома (а), двух атомов, связанных химической связью (б), и периодического потенциала одномерной решётки (в).

Так как в кристалле атомы (атомные остатки, ионы) расположены строго периодически, то полный потенциал кристалла V(r) должен обладать трехмерной периодичностью. В общем случае, точный вид периодического потенциала V(r) неизвестен. Однако тот факт, что V(r) является периодической функцией, период которой совпадает с периодом кристаллической решетки, то есть:

где g – вектор трансляции решетки (на рис. 1.41 —g=n·a, где n – целое число), позволяет получить два фундаментальных результата:

Первый.Из условия трансляционной симметрии следует, что волновая функция электрона в точке rотличается от волновой функции электрона в точке r+g некоторым множителем С.

(1.48)

Из условия нормировки следует, что

(1.49)

Условию (1.49) можно удовлетворить, если положить

С = exp(i·k·g) (1.50)

Здесь k-постоянный вектор, характеризующий квантовое состояние электрона в кристалле, называется волновым вектором. Вектор трансляции g имеет размерность длины, k·g— безразмерное, следовательно и

На основании соотношений (1.47) и (1.49), можно показать, что волновая функция электрона в кристалле имеет вид:

, (1.51)

где — периодическая функция, — плоская волна, идущая в направлении вектора k.

Волны, описываемые соотношением (1.51), носят название волн Блоха. Волна Блоха представляет собой плоскую волну, модулированную периодической функцией , имеющей период решетки и зависящий от волнового вектора k. Волновой векторk задает направление распространение плоской волны. Физический смысл волнового вектора k – число длин волн, укладывающихся на отрезке 2p.

Выбор формы представления стационарной волновой функции электрона в кристалле в виде волны Блоха следует из периодичности кристаллической решетки, а именно, с учетом формул 1.48-1.50:

Где функция обладает трехмерной периодичностью кристаллической решетки т. к., если взять любой произвольный вектор трансляции кристаллической решетки q₁

Т.е.

Таким образом: стационарная волновая функция электронов в периодическом поле кристалла зависит от волнового вектора и имеет вид , где — плоская волна, бегущая в направлении , а функция координат — функция координат, зависящая от волнового вектора и имеющая периодичность решетки.

Второй результат является следствием неоднозначности волнового вектора k для электрона в кристалле. Чтобы показать это, рассмотрим трансляционное условие:

(1.52)

Это условие не нарушится, если волновой вектор k заменить на вектор k+2pК, где

. (1.53)

Где вектор К – вектор обратной решетки.

Следовательно, состояния, характеризуемые волновым вектором k и k+ 2pК физически эквивалентны. То есть энергия электронов, находящихся в этих двух= состояниях одинакова. Другими словами, и волновая функция и энергия электрона в кристалле являются периодическими функциями волнового вектора k с периодом 2pК:

(1.54)

(1.55)

Если в k -пространстве (или в P-пространстве) построить обратную решетку, растянутую в 2p раз, то есть решетку с векторами 2pb₁ , 2pb₂ , 2pb₃ (или , , ) то все k -пространство можно разделить на области, в которых имеются физически эквивалентные состояния. Эти области называются зонами Бриллюэна.

Многогранник минимального объема, построенный вокруг начала координат в k-пространстве, содержащей все возможные различные состояния, называют первой или основной зоной Бриллюэна. С помощью векторов обратной решетки любую точку k -пространства можно перевести в первую зону Бриллюэна.

Рис. 1.42. Первая зона Бриллюэна для кристалла с простой кубической (а), кубической объемно-центрированной (б) и кубической гране-центрированной (в).

источники:

http://elementy.ru/trefil/21/Uravnenie_Shryodingera

http://megapredmet.ru/1-49664.html