Приближенное дифференциальное уравнение оси изогнутой оси балки

Дифференциальное уравнение оси изогнутой балки

Для определения уравнения оси изогнутой балки воспользуемся законом Гука:

.

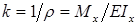
Выражение для кривизны некоторой кривой:

.

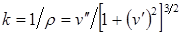
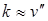
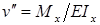
В пределах упругих деформаций квадрат угла поворота поперечного сечения балки ничтожно мал по сравнению с единицей. Поэтому (вторая производная от прогиба представляет собой кривизну изогнутой оси балки ( уравнение изгиба ) в рассматриваемом месте балки:.

Продифференцировав полученное уравнение дважды по z, получим дифференциальное уравнение оси изогнутой балки : .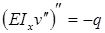

Интегрирование дифференциального уравнения оси изогнутой балки

Интегрируя дифференциальное уравнение оси изогнутой балки первый раз, получим выражение, дающее закон изменения поперечной силы по длине балки.

Второе интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения изгибающего момента.

Третье интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения углов поворота поперечных сечений.

Четвертое интегрирование дифференциального уравнения оси изогнутой балки определяет закон изменения прогибов балки по ее длине.

Постоянные интегрирования определяются из условий закрепления балки.

СОПРОМАТ ОН-ЛАЙН

Меню сайта

Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.

Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!

Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.

Лекции — теория, практика, задачи.

Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое.

Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).

Книги — разная литература по теме.

Базовый курс лекций по сопромату, теория, практика, задачи.

4. Изгиб. определение перемещений.

4.1. Дифференциальное уравнение изогнутой оси балки и его интегрирование.

При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки.

Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .

В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .

Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):

.

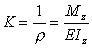
В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

.

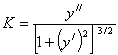
Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем

.

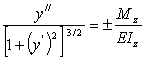
Это равенство называется дифференциальным уравнением упругой линии. При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

.

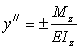
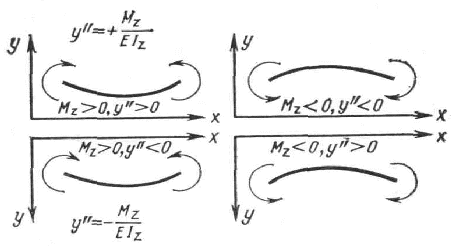
Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.

Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.

Интегрируя (8.29), находим сначала углы поворота сечений

,

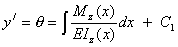
а после второго интегрирования – прогибы балки

.

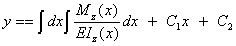
Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.

Дифференциальное уравнение оси изогнутой балки

Имеем закон Гука при изгибе: , где r(х) — радиус кривизны изогнутой оси балки в сечении х, М(х) — изгибающий момент в том же сечении, EJ — жесткость балки. Из высшей математики известно: — дифференциальное уравнение изогнутой оси балки. — тангенс угла между осью х и касательной к изогнутой оси. Эта величина очень мала (прогибы балки малы) Þ ее квадратом пренебрегают и угол поворота сечения приравнивают тангенсу. Приближенное дифференциальное ур-ние изогнутой оси балки: . Если ось y направлена вверх, то знак (+). В некоторых вузах ось y направляется вниз Þ(—). Интегрируя дифф. уравнение, получаем: — ур-ние углов поворота, интегрируем второй раз: — получаем ур-ние прогибов.

ИЛИ
Для определения уравнения оси изогнутой балки воспользуемся законом Гука:

.

Выражение для кривизны некоторой кривой:

.

В пределах упругих деформаций квадрат угла поворота поперечного сечения балки ничтожно мал по сравнению с единицей. Поэтому (вторая производная от прогиба представляет собой кривизну изогнутой оси балки (уравнение изгиба) в рассматриваемом месте балки: .

Продифференцировав полученное уравнение дважды по z, получимдифференциальное уравнение оси изогнутой балки: .

ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ОСИ ИЗОГНУТОЙ БАЛКИ

Интегрируя дифференциальное уравнение оси изогнутой балки первый раз, получим выражение, дающее закон изменения поперечной силы по длине балки.

Второе интегрирование дифференциального уравнения оси изогнутой балкиопределяет характер изменения изгибающего момента.

Третье интегрирование дифференциального уравнения оси изогнутой балкиопределяет характер изменения углов поворота поперечных сечений.

Четвертое интегрирование дифференциального уравнения оси изогнутой балки определяет закон изменения прогибов балки по ее длине.

Постоянные интегрирования определяются из условий закрепления балки

10.Определение прогибов и углов поворотапоперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

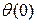
11.Косым изгибом называется вид нагружения, при котором плоскость действия изгибающего момента не проходит ни через одну из главных осей сечения.

Напряжения и перемещения при косом изгибе найдем, используя принцип независимости действия сил. Косой изгиб рассматривается при этом как одновременный изгиб в 2-х плоскостях zx и zy. Для этого изгибающий момент М_изг раскладывается на составляющие моменты осей х и у.

Нормальные напряжения в любой точке поперечного сечения могут быть вычислены как алгебраическая сумма напряжений, возникающих от моментов M_x и M_y:

a — угол отклонения плоскости действия M от вертикали.

Если в каждой точке сечения отложить по нормали вектор сигма, то концы векторов, как и при простом изгибе образуют плоскость. Уравнение нейтральной линии в сечении найдем, полагая сигма=0:

При косом изгибе нейтральная линия не перпендикулярна к плоскости изгибающего момента

14. Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент. Прочие силовые факторы (изгибающие моменты, нормальная и поперечные силы) равны нулю.

Расчётная схема закрученного образца:

— полный угол закручивания.

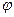
Берём элементарный участок:

— относительный угол поворота, приходящийся на единицу длины.

зависит от радиуса поперечного сечения круглого стержня.

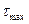
Внутренняя сила в точке К определяется

— полярный момент инерции поперечного сечения – геометрическая характеристика, зависящая от размеров поперечного сечения.

— зависимость при кручении.

15. Обобщённые силы и обобщенные перемещения

В механике мы различаем два самостоятельных силовых фактора — сосредоточенные силы Р, пару сил с моментом m (рис. 12.1, а). Иногда приходится иметь дело с группой сил и моментов. Назовём обобщённой силой Р группу сил или моментов, характеризуемых одним параметром или числом. На рис.12.1, б,в,г обобщёнными силами будут две силы Р, два момента m, распределённая нагрузка q.

А) б)

В) г)

Рис. 12.1

Производимая ими работа соответственно равна:

где а величина представляет собой площадь между исходной и изогнутой осями балки.

Обобщённым перемещениемназовём множители , стоящий в выражении работы при обобщённой силе и .

Таким образом, под обобщенной силой будем понимать любую нагрузку (сосредоточенные силы, сосредоточенные пары, распределенную линейную нагрузку, распределенную моментную нагрузку), а под обобщенным перемещением – тот вид перемещения, на котором обобщенная сила производит работу.

Обобщёнными силами могут быть не только внешние, но и внутренние:

Рассмотрим например статически неопределимую балку (рис. 12.2).

Рис. 12.2

Рассечём её на расстоянии z от левого конца и приложим к краям разреза по две нормальные силы N, две перерезывающие , два изгибающих момента , каждая из которых образует группу сил, характеризуемых одним числом, т.е. обобщённую силу.

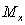
Возьмём две нормальные силы N. Они совершат работу:

Обобщённое перемещение представляет собой относительное расхождение краёв разреза. Аналогично можно рассмотреть две силы и два момента .

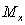
Обобщенные перемещения принято обозначать буквами или с двумя индексами. Первый индекс обозначает точку и направление перемещения, а второй указывает причину, вызвавшую искомое перемещение. Например, обозначает перемещение точки приложения силы F по направлению ее действия, вызванное этой же силой.

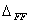
Для обозначения полного перемещения точки, вызванного несколькими обобщенными силами, при сохраняется только первый индекс.

Перемещение, вызванное безразмерной единичной силой или безразмерной единичной парой , обозначается символом и называется удельным. Потенциальная энергия бруса в общем случае нагружения.

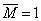
Общий случай нагружения бруса , когда в поперечных сечениях возникают нормальные и поперечные силы , изгибающие и крутящие моменты одновременно .

При разгрузке тела за счет потенциальной энергии производится работа.

Упругое тело является аккумулятором энергии.

Работа силы на упругом перемещении определяется половиной произведения наибольшего значения силы и перемещения ΔL .

Если бы между силой и перемещением не было прямой пропорциональности, вместо коэффициента ½ был бы получен какой –то другой коэффициент. В частности при постоянной силе он равен единице.

Исключая из полученного для U выражения ΔL, найдем

Энергия упругих деформаций стержня при изгибе определяется работой момента М на взаимном угловом перемещении dθ двух сечений.

Если нормальная сила N меняется вдоль оси стержня, то потенциальная энергия деформации должна определяться суммированием по участкам dz. Для элементарного участка dU = N 2 dz/2EF,а для всего стержня

Энергетическое соотношение широко используется при определении перемещения в сложных упругих системах.

17.Найдём работу которую совершают силы Р1 и Р2 в случайном приложении в различном порядке: А=1\2(Р1* ) +1\2(Р2 ;
А=1\2(Р2* ) +1\2(Р1 ; => Р2* А2=Р1* В1 — теорема Бетти
Работа первой силы на перемещение её точки приложено под действием второй силы равно работе второй силы на перемещение точки её приложения под действием первой силы.

18.Теорема Кастильяно не позволяет определить перемещения не в точках приложения сил. Если необходимо найти перемещение точки к которой не приложены внешние силы, то мы прикладываем в этой точке внешнюю силу Ф в инерциальное направление. Составим выражение для потенциальной энергии . Дальше по теореме Кастильяно находим производную получая соответственно . При этом считаем Ф=0. В поперечном сечении при приложении силы пропорциональной Ф. Будут возникать силовые факторы
Мк=Мкр+Мк1 * Ф где: Мкр — крутящий момент от заданной нагрузки; Мк1 — коэф. пропорц.
где где — искомое перемещение (линейное или угловое);

Мp, М1 — аналитические выражения изгибающих моментов соответственно от заданной и единичной cилы;

EJх — жесткость сечения балки в плоскости изгиба.

19. При вычислении интегралов вместо аналитических выражений моментов используются их эпюры. Т.е. значение можно найти по способу Верещагина, «перемножив» эпюры Мp и М1.

Перемножить две эпюры — значит площадь нелинейной эпюры изгибающих моментов умножить на ординату другой обязательно линейной эпюры, находящейся под центром тяжести первой, и результат разделить на жесткость (в случаях, когда на данном участке обе эпюры линейны, совершенно безразлично, на какой из них брать площадь, а на какой ординату).

где Ω — площадь произвольной фигуры; Мc — ордината прямолинейной эпюры, соответствующей центру тяжести площади Ω

20.Статично невизначені стержневі системи. Вибір основної системи: Под стержневой системою понимают конструкцію елементами которой является стержень. В случае если стержени работают на растяжение сжатие то такая конструкція називается фермой, если стержни работают на кручение или изгиб то такая конструкція називается рамой.Статически определимой системой називают системи в которих число ур. Равновесия равно числу неизвестних реакций связи, если число неизвестних реакцій свіязей більше числа ур. Равновесия то такая система назив.статически неопределимой, при етом разность между етими числами назив. степеню неопределимости системи.

22.Нерозрізні балки.Рівняння трьох моментів.Способ раскрития статической неопределимости основан на врезании дополнительних шарниров что как известно приводит к снижению статической неопределимости на число равное числу дополнительних шарниров.Число дополнительних условий также равно числу дополнительних шарниров. Теорема о 3 моментахпредпологает что дополнительние шарніри врезаются на лишних опорах, получим соотношение для неизвестних моментов которие возникают в данном случае этих дополнительних шарнірах: