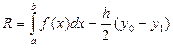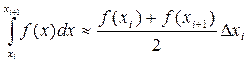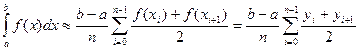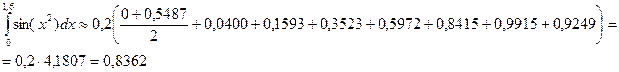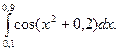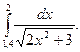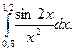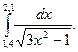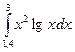Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений
Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ \begin
Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ \begin
Численные методы решения задачи Коши
Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
Идея численных методов решения задачи (3), (4) состоит из четырех частей:
1. Вводится расчетная сетка по переменной \( t \) (время) из \( N_t + 1 \) точки \( t_0 \), \( t_1 \), \( \ldots \), \( t_
2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.
3. Аппроксимируем производные конечными разностями.
4. Формулируем алгоритм, который вычисляет новые значения \( \pmb
Явный метод Эйлера
Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами \( t_n \) и \( t_
Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ \pmb^\prime (t_n) = \pmb
Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ \pmb^\prime(t) = \lim_ <\tau \to 0>\frac<\pmb(t+\tau) — \pmb(t)><\tau>. $$
В произвольном узле сетки \( t_n \) это определение можно переписать в виде: $$ \begin
Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение \( y^n \) для того, чтобы решить уравнение (5) относительно \( y^
При условии, что у нас известно начальное значение \( \pmb
Программная реализация явного метода Эйлера
Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом
При решении системы (векторный случай), u[n] — одномерный массив numpy длины \( m+1 \) (\( m \) — размерность задачи), а функция F должна возвращать numpy -массив размерности \( m+1 \), t[n] — значение в момент времени \( t_n \).
Таким образом численное решение на отрезке \( [0, T] \) должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.
Функция euler решения системы уравнений реализована в файле euler.py:
Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .
Неявный метод Эйлера
При построении неявного метода Эйлера значение функции \( F \) берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ \begin
Таким образом для нахождения приближенного значения искомой функции на новом временном слое \( t_
Для решения уравнения (8) можно использовать, например, метод Ньютона.
Программная реализация неявного метода Эйлера
Функция backward_euler решения системы уравнений реализована в файле euler.py:
Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .
Методы Рунге—Кутта
Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ \begin
Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ \begin
Многошаговые методы
В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах \( \pmb
Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ \begin
Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции \( \pmb
Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен \( m+1 \).
Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям \( \pmb
Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет \( m \)-ый порядок.
На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ \frac<\pmb
Жесткие системы ОДУ
При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке \( u = w \) передаются линейной системой $$ \begin
Пусть \( \lambda_i(t) \), \( i = 1, 2, \ldots, m \) — собственные числа матрицы $$ \begin
Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование \( A \)-устойчивых или \( A(\alpha) \)-устойчивых методов.
Метод называется \( A \)-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ \begin
Приближенное решение обыкновенных дифференциальных уравнений. Метод Эйлера
Практическое занятие №25
«Численное интегрирование с помощью формул прямоугольников, трапеций, Симпсона.
Приближенное решение дифференциальных уравнений с помощью формул Эйлера»
1. Цель: Выработать навыки и умения по применению методов приближённого
интегрирования – формул прямоугольников, трапеций и Симпсона, в решении
приближенными методами дифференциальных уравнений
Пояснения к работе
2.1 Краткие теоретические сведения:
Формула прямоугольников
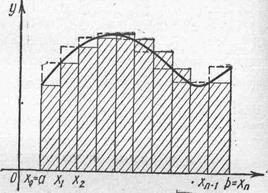
Известно, что не для всякой непрерывной функции ее первообразная выражается через элементарные функции. Кроме того, на практике сталкиваются с необходимостью вычислять интегралы от функций, заданных табличным или графическим способами, а так же интегралы от функций, первообразные которых выражаются через элементарные очень сложно, что требует большой вычислительной работы и с практической точки зрения нерационально. В этих случаях вычисление определенного интеграла по формуле Ньютона – Лейбница затруднительно, поэтому прибегают к различным методам приближенного интегрирования. Наиболее простым методом приближенного вычисления определенного интеграла является метод прямоугольников, основанный на непосредственном определении интеграла:
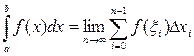
где 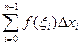
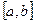
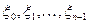
Вычисление определенного интеграла 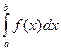
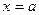
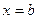
Для точности численного интегрирования нужно отрезок 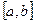

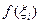
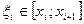
интеграла на отрезке 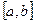
Практически удобно делить отрезок 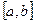
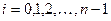
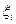
левыми 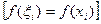
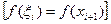
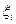
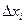
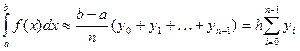
где 
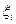
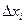

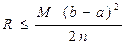
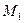
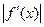
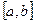
Пример 1. Используя формулу прямоугольников при 

Решение: разделим отрезок 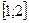
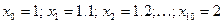

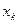 | 1 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2 |
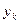 | 1.000 | 0.909 | 0.833 | 0.769 | 0.714 | 0.667 | 0.625 | 0.588 | 0.556 | 0.526 | 0.5 |
Тогда получим 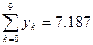
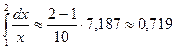
Оценим погрешность. Имеем 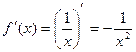
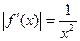
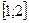
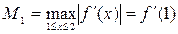

Так как допущенная погрешность влияет уже на второй знак после запятой, то третий знак следует округлить. Значит, 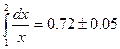
Лейбница, то получим 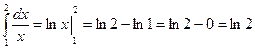
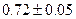

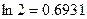
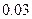
Формула трапеций
Приближенное значение определенного интеграла можно вычислить и иным способом.
Заменим на отрезке 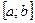
интеграла численно равным площади этой трапеции.
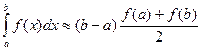
Это и есть формула трапеций для приближенного вычисления интеграла. Погрешность вычисления
для формулы трапеций оценивается так:
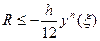
где точка 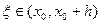
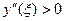
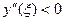
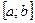
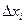
Для простоты вычислений удобно делить отрезок 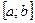
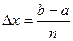
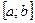
Эта формула называется общей формулой трапеций. Общую формулу трапеций можно переписать в более удобном виде:
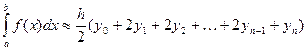

Пример 2.Вычислить интеграл 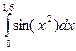
Решение: составим таблицу значений подынтегральной функции при 
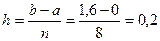
 | 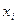 | 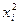  | 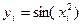 | 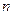 | 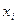 | 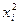 | 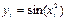 |
| 0,2 0,4 0,6 | 0,02 0,16 0,36 | 0,0000 0,0400 0,1593 0,3523 | 0, 1,0 1,2 1,4 1,6 | 0,64 1,0 1,44 1,96 2,56 | 0,5972 0,8415 0,9915 0,9249 0,5487 |
Используя формулу 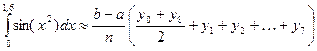
Находим:
Примечание. Если данный интеграл вычислить при 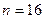
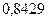
Формула Симпсона
Точность приближенного интегрирования заметно возрастает, если подынтегральную функцию 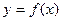
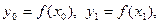
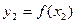
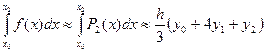
Соотношение (7) называется формулой Симпсона. Формула Симпсона обладает повышенной точностью и является точной не только для многочленов второй степени, но и третьей. Погрешность формулы Симпсона оценивается следующим образом:
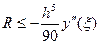
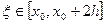
Для увеличения точности вычислений отрезок 
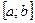
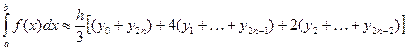
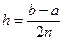
Соотношение (9) называется общей формулой Симпсона.
Пример 3. Вычислить по формуле Симпсона 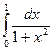
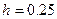
По формуле (9) имеем 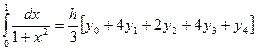
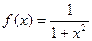
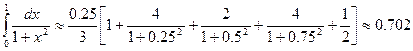
Приближенное решение обыкновенных дифференциальных уравнений. Метод Эйлера
Простейшим обыкновенным дифференциальным уравнением является уравнение первого порядка, разрешенное относительно производной:

Основная задача, связанная с этим уравнением, известна как задана Коши:найти решение уравнения (10) в виде функции у(х), удовлетворяющей начальному условию

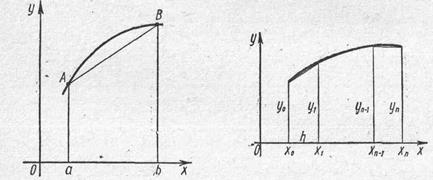
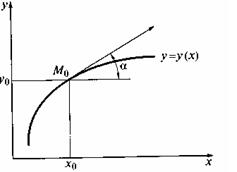
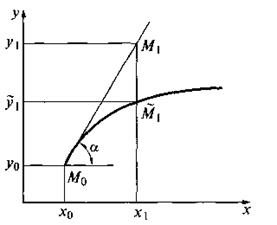
Геометрически это означает, что требуется найти интегральную кривую у = у(х), проходящую через
заданную точку M0(x0, .y0), при выполнении равенства (11) (см. рис.6). С численной точки зрения задача Коши выглядит следующим образом: требуется построить таблицу значений функции у=у(х), удовлетворяющей уравнению (10) и начальному условию (11) на отрезке [a;b]с некоторым шагом h. Обычно считается, что х0 = а, т.е. начальное условие задано в левом конце отрезка.
Простейшим из численных методов решения дифференциальных уравнений является метод Эйлера.В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.
Пусть дано уравнение (10) с начальным условием (11) (т.е. поставлена задача Коши). Решим вначале следующую задачу: найти простейшим способом приближенное значение решения в некоторой точке x1 = х0 + h, где h — достаточно малый шаг.
Заметим, что уравнение (10) совместно с начальным условием (11) задают направление касательной к искомой интегральной кривой в точке М0(х0, у0). Уравнение касательной имеет вид
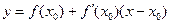
Двигаясь вдоль этой касательной (рис. 7), учитывая соотношения (10) и (12), получим приближенное значение решения в точке х1:
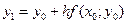
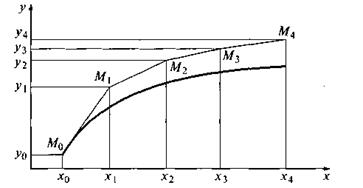
Располагая приближенным решением в точке М1 (х1,y1), можно повторить описанную ранее процедуру: построить прямую, проходящую через эту точку с угловым коэффициентом f (х1, y1) и по ней найти приближенное значение решения в точке х2 = х1 + h. Заметим, что в отличие от ситуации, изображенной на рис. 7, эта прямая не есть касательная к реальной интегральной кривой, поскольку точка M1, нам недоступна. Однако представляется интуитивно ясным, что если h достаточно мало, то получаемые приближения будут близки к точным значениям решения.
Продолжая эту идею, построим систему равноотстоящих точек
Получение таблицы значений искомой функции у(х) по методу Эйлера заключается в циклическом
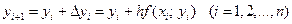
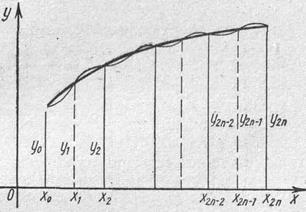
Геометрическая иллюстрация метода Эйлера приведена на рис. 8. Вместо интегральной кривой в реальности получается совокупность прямых (так называемая ломаная Эйлера).
Рис.8 Ломаная Эйлера
Методы численного интегрирования дифференциальных уравнений, в которых решение получается от одного узла к другому, называются пошаговыми. Метод Эйлера — простейший представитель семейства пошаговых методов.
Отметим, что оценка погрешности метода при таком элементарном рассмотрении невозможна даже на первом шаге. Кроме того, особенностью любого пошагового метода является то, что, начиная со второго шага исходное значение у, в формуле (13) само является приближенным, т.е. погрешность на каждом следующем шаге систематически возрастает.
Наиболее используемым эмпирическим методом оценки точности как метода Эйлера, так и других пошаговых методов приближенного численного интегрирования обыкновенных дифференциальных уравнений является способ двойного прохождения заданного отрезка — с шагом h и с шагом h/2. Совпадение соответствующих десятичных знаков в полученных двумя способами результатах дает эмпирические основание считать их верными (хотя полной уверенности в этом быть не может).
Одна из принципиальных трудностей всех пошаговых методов численного решения дифференциальных уравнений состоит в возможности столкнуться с неустойчивостью метода. Оценка погрешности неявно предполагает, что ломаная приближенного решения (см. рис. 8) хотя и не совпадает с интегральной кривой, но качественно на нее похожа. Чаще всего это именно так, но иногда (например, при неудачном выборе шага h) приближенное решение может быть качественно непохожим на точное (например, точное монотонно убывает, а приближенное монотонно возрастает).
Для эмпирического контроля того, не имеет ли места неустойчивость, следует численно интегрировать уравнение с несколькими, значительно отличающимися, значениями шага h, сравнивая качественно поведение решений.
Пример 4.Применяя метод Эйлера, составить таблицу значений решения дифференциального уравнения 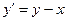
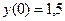
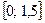
Для удобства вычислений составим таблицу.
1-й шаг: по начальным условиям заполним первую строку во 2-м и 3-м столбцах ;
2-й шаг: из уравнения 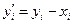
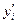
3-й шаг: содержимое столбца (4) умножаем на h (вычисляем 
записываем результат в столбец (5) этой же строки;
4-й шаг: к содержимом столбца (3) прибавляем содержимое столбца (5) этой же строки
(вычисляем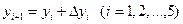
строки. Определяем хi+1 = xi + h и затем шаги 2-4 повторяем до тех пор, пока не будет пройден
весь отрезок 
| i | xi | yi | 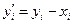 |  |
| (1) | (2) | (3) | (4) | (5) |
| 1,5000 | 1,5000 | 0,3750 | ||
| 0,25 | 1,8750 | 1,6250 | 0,4062 | |
| 0,50 | 2,2812 | 1,7812 | 0,4453 | |
| 0,75 | 2,7265 | 1,9765 | 0,4951 | |
| 1,00 | 3,2206 | 2,2206 | 0,5552 | |
| 1,25 | 3,7758 | 2,5258 | 0,6314 | |
| 1,50 | 4,4072 |
Пример 5. Решить методом Эйлера дифференциальное уравнение 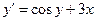
Решение: результаты вычислений с двумя знаками после запятой приведены в таблице:
| i | xi | yi | 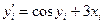 | 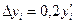 |
| (1) | (2) | (3) | (4) | (5) |
| 0,0 | 1,3 | 0,27 | 0,05 | |
| 0,2 | 1,35 | 0,82 | 0,16 | |
| 0,4 | 1,51 | 1,25 | 0,25 | |
| 0,6 | 1,76 | 1,61 | 0,32 | |
| 0,8 | 2,08 | 1,91 | 0,38 | |
| 1,0 | 2,46 |
Задание
Вариант 1
1.По формуле левых прямоугольников для n=12 вычислить значение интеграла: 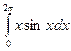
2. По формуле трапеций n=10 вычислить значение интеграла с тремя десятичными
знаками: 
3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками: 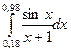
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
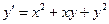
Сделайте ручную прикидку графика интегральной кривой на бумаге.
Вариант 2
1.По формуле левых прямоугольников для n=12 вычислить значение интеграла: 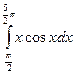
2.По формуле трапеций n=8 вычислить значение интеграла с тремя десятичными
знаками: 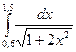
3.По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками: 
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
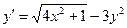
Сделайте ручную прикидку графика интегральной кривой на бумаге.
Вариант 3
1.По формуле правых прямоугольников для n=12 вычислить значение интеграла:
2.По формуле трапеций для n=10 вычислить значение интеграла с тремя десятичными
знаками:
3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками:
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
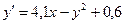
Сделайте ручную прикидку графика интегральной кривой на бумаге.
Вариант 4
1.По формуле правых прямоугольников для n=12 вычислить значение интеграла:
2. По формуле трапеций для n=10 вычислить значение интеграла с тремя десятичными знаками:
3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками:
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
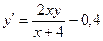
Сделайте ручную прикидку графика интегральной кривой на бумаге.
4. Контрольные вопросы:
1. Какие методы приближенного вычисления определенных интегралов вы знаете? Назовите
формулы для вычислений. Какой из них дает наиболее точный результат?
2. На чем основан метод Эйлера приближенно решения дифференциальных уравнений?
5. Содержание отчёта:
5.1 Наименование работы
5.4 Формулы для расчета
5.5 Необходимые расчеты. Анализ результатов расчетов
5.6 Выводы по работе
5.7 Ответы на контрольные вопросы
1. Колягин Ю.М. , Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах Учебное пособие — М.
Новая волна, 2005, ч.1, с.565-571;
2. Богомолов Н.В. «Практические занятия по математике» — Учебное пособие – М.:Высш. школа,
3. Лапчик М.П., Рагулина М.И., Хеннер Е.К. Элементы численных методов: учебник для студ. сред.
проф. образования -М.: Издательский центр «Академия», 2007, с.152-184
ЛЕКЦИЯ Приближенное решение обыкновенных дифференциальных уравнений: Метод Эйлера. — презентация
Презентация была опубликована 8 лет назад пользователемИван Ергин
Похожие презентации
Презентация на тему: » ЛЕКЦИЯ Приближенное решение обыкновенных дифференциальных уравнений: Метод Эйлера.» — Транскрипт:
1 ЛЕКЦИЯ Приближенное решение обыкновенных дифференциальных уравнений: Метод Эйлера
2 Дифференциальные уравнения устанавливают связь между независимыми переменными, искомыми функциями и их производными. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным. Постановка задачи
3 Например, структура движения потока в реакторе идеального перемешивания описывается обыкновенным дифференциальным уравнением: Здесь искомая функция (концентрация вещества) С(t) зависит от одной переменной t (времени).
4 Постановка задачи В том случае, если искомая функция зависит от нескольких переменных, дифференциальное уравнение будет уравнением в частных производных. Например, структуру потока в реакторе идеального вытеснения можно описать уравнением в частных производных: В этом уравнении функция С(t,l) зависит от времени (t) и длины аппарата (l).
5 Постановка задачи Обыкновенными дифференциальными уравнениями (ОДУ) называются уравнения, которые содержат одну или несколько производных от искомой функции y = y(x): где x – независимая переменная. Наивысший порядок n, входящей в уравнение производной, называется порядком дифференциального уравнения. Например: уравнение первого порядка; уравнение второго порядка
6 Постановка задачи Из общей записи дифференциального уравнения можно выразить производную в явном виде: Уравнение для производных имеет бесконечное множество решений. Для получения единственного решения необходимо указать дополнительные условия, которым должны удовлетворять искомые решения.
7 Постановка задачи В зависимости от вида таких условий рассматривают три типа задач, для которых доказано существование и единственность решений. Первый тип – это задачи с начальными условиями. Для таких задач кроме исходного дифференциального уравнения в некоторой точке x 0 должны быть заданы начальные условия, т.е. значения функции y (x) и её производных: y (x 0 ) = y 0 y’ (x 0 ) = y ‘ 0. y (n-1) (x 0 ) = y n-1 0.
8 Постановка задачи Второй тип задач – это, так называемые, граничные, или краевые, в которых дополнительные условия задаются в виде функциональных соотношений между искомыми решениями. Третий тип задач для обыкновенных дифференциальных уравнений – это задачи на собственные значения.
9 Постановка задачи Сформулируем задачу Коши. Дано обыкновенное дифференциальное уравнение (ОДУ) первого порядка, разрешенное относительно производной удовлетворяющее начальному условию
10 Постановка задачи Необходимо найти на отрезке [x 0,x n ] такую непрерывную функцию y = y(x), которая удовлетворяет дифференциальному уравнению и начальному условию т.е. найти решение дифференциального уравнения. Нахождение такого решения называют решением задачи Коши. Численное решение этой задачи состоит в построении таблицы приближенных значений y 1,y 2. y n решения уравнения y(x) в точках x 1,x 2. x n с некоторым шагом h.
11 Методы Рунге-Кутта Методы Рунге-Кутта обладают следующими отличительными свойствами: являются одноступенчатыми: чтобы найти значение функции в точке y i+1 нужна информация только о предыдущей точке (y i,x i ); согласуются с рядом Тейлора вплоть до членов порядка h k, где степень k определяет порядок метода; не требуют вычисления производных от f(x,y), а требуют вычисления самой функции.
12 Метод Эйлера (метод Рунге-Кутта первого порядка) Простейшим из численных методов решения дифференциальных уравнений является метод Эйлера. Это один из самых старых и широко известных и применяемых на в практике методов.
13 Метод Эйлера Пусть требуется найти приближенное решение дифференциального уравнения первого порядка с начальным условием y(x 0 )=y 0, т.е. необходимо решить задачу Коши.
14 Метод Эйлера В окрестности точки x 0 функцию y(x) разложим в ряд Тейлора который можно применить для приближенного определения искомой функции y(x). В точке x 0 +h при малых значениях h можно ограничиться двумя членами ряда, тогда, где O(h 2 ) – бесконечно малая величина порядка h 2. (1) (2)
15 Метод Эйлера Заменим производную y'(x 0 ), входящую в формулу (1), на правую часть уравнения (2) Приближенное решение в точке x 1 =x 0 +h можно вновь рассматривать как начальное условие и по формуле найти значение искомой функции в следующей точке x 2 =x 1 +h. В результате получен простейший алгоритм решения задачи Коши, который называется методом Эйлера.
16 Метод Эйлера Метод Эйлера можно представить в виде последовательного применения формул: для точки x 1 = x 0 +h, x 2 = x 1 + h, x i+1 = x i + h,
17 Метод Эйлера Таким образом, формула Эйлера в общем случае имеет вид: x i+1 = x i + h
18 Метод Эйлера Геометрически искомая функция y(x) заменяется ломаной линией, представляющей собой отрезки касательных к этой функции в узлах x 0, x 1. x n.
19 x0 x0 y=y 0 +y 0 ‘(x–x 0 ) y h x1 x1 y0y0 y1y1
20 Метод Эйлера Выведем формулы на основе геометрических аналогий. Предположим, что нам известна точка (x 0,y 0 ) на искомой интегральной кривой. Через точку (x 0,y 0 ) проведем касательную с тангенсом угла наклона (3) Уравнение касательной имеет вид:
21 Метод Эйлера Тогда в точке x 1 =x 0 +h, с учетом (3) получим решение: Ошибка решения в точке x=x 1 показана в виде отрезка.
22 Метод Эйлера Полученная формула является методом Рунге — Кутта первого порядка, т.к. она согласуется с разложением в ряд Тейлора вплоть до членов порядка h 1. Метод Эйлера имеет довольно большую погрешность вычисления: 0(h). Кроме того, он очень часто оказывается неустойчивым – малая ошибка (например, заложенная в исходных данных) увеличивается с ростом x.
http://lektsii.org/4-22486.html
http://www.myshared.ru/slide/616153/