Приближенное решение уравнений 3 метода

Приближенное вычисление корней в уравнениях

Приближенное вычисление корней в уравнениях

Приближённое решение уравнений :

1.1 Способ хорд (или способ линейной интерполяции).

1. Способ касательных (или способ Ньютона).
2. Комбинированный способ (комбинированное применение способов хорд и касательных).

Приближённое решение уравнений.

Если квадратные уравнения решали уже древние греки, то способы решения алгебраических уравнений третьей и четвёртой степени были открыты лишь в XVI веке. Эти классические способы дают точные значения корней и выражают их через коэффициенты уравнения при помощи радикалов различных степеней. Однако эти способы приводят к громоздким вычислениям и поэтому имеют малую практическую ценность.

В отношении алгебраических уравнений пятой и высших степеней доказано, что в общем случае их решения не выражаются через коэффициенты при помощи радикалов. Не выражаются в радикалах, например, корни уже такого простого по виду уравнения, как:

Сказанное, однако, не означает отсутствия в науке методов решения уравнения высших степеней. Имеется много способов приближенного решения уравнений — алгебраических и неалгебраических (или, как их называют, трансцендентных), позволяющих вычислять их корни с любой, заранее заданной степенью точности, что для практических целей вполне достаточно.

На простейших из таких способов мы и остановимся, причём речь будет идти о вычислении действительных корней.

Пусть нужно решить уравнение:

Если обратиться к рисунку, то каждый корень уравнения (1) представляет собой абсциссу точки пересечения графика функции y=f(х)

C осью Ох (рисунок №1)

С помощью графика функции или каким-нибудь иным способом обычно удаётся установить приблизительные значения корней. Это позволяет для каждого корня получить грубые приближения по недостатку и по избытку. Такого рода грубых приближений во многих случаях оказывается достаточно, чтобы, отправляясь от них, получить все значения корня с требуемой точностью. Об этом и пойдёт речь.

Итак, пусть корень Е уравнения (1) «зажат» между двумя его приближениями а и b по недостатку и по избытку а

Способ хорд (или способ линейной интерполяции).

Проведём хорду АВ (рисунок№3) и за первое приближённое значение корня примем абсциссу x1 точки С пересечения хорды с осью Ох.

Уравнение хорды имеет вид:

Поэтому в точке С:

Рассмотрение всех четырёх случаев, изображённых на рисунке №2, показывает, что точка x1 лежит между a и b с той стороны от Е, где f(х) имеет знак, противоположный знаку f«(х).

Остановим внимание на первом случае: f`(х)>0, f«(х)>0 (рисунок №3), — в остальных случаях рассуждение вполне аналогично. В этом первом случае x1 лежит между a и Е. С отрезком [x1, b] поступаем так же, как мы поступаем с отрезком [a, b] (рисунок №4). При этом для нового приближённого значения корня получаем:

x1 = x2-(b- x1)*f(x1)/f(b)-f(x1)

( в формуле (2) заменяем x1 на x2, а на x1 ); значение x2 оказывается между x1 и Е. Рассматриваем отрезок [x2, b] и находим новое приближённое x3, заключённое между x2 и Е и. т. д. В результате получим последовательность а 0

Найдём первое приближённое значение корня по формуле (2):

так как f(1,588)=-0,817 0

Следовательно, искомый корень с точностью до 0,01 равен 1,64.

1.2 Способ касательных (или способ Ньютона).

В том из концов дуги АВ (рисунок №5), в котором знаки f(х) и f«(х) совпадают, проводим касательную и за первое приближённое значение корня принимаем абсциссу х1` точки Д пересечения этой касательной с осью Ох. Обратимся вновь к первому случаю, соответствующему первому рисунку №2 (f`(x)>0, f«(x)>0), — в остальных случаях рассуждают опять-таки аналогично. Уравнение интересующей нас касательной имеет вид:

и поэтому в точке Д:

Из рисунка видно, что x1` лежит между Е и b. С отрезком [a, x1`] поступаем так же, как с отрезком [a, b] ( рисунок №5), и в результате для нового приближённого значения корня получим:

х2` = x1`- f( x1`)/ f`( x1`).

Значение х2` оказывается между Е и x1`. Рассматриваем отрезок [a, х2`] и находим новое приближение х3` и т. д. В результате получим последовательность:

все более точных приближённых значений корня, причём:

xn+1`= xn`- f(xn`)/ f`( xn`) (8)

Эта формула справедлива для всех четырёх случаев, изображённых на рисунке 32. Для оценки погрешностей полученных приближений можно опять воспользоваться формулой (5), как и в первом случае, легко устанавливается сходимость последовальности x1`, х2`, х3`,…,xn`,… к значению Е

Пример №2. Методом касательных найдём положительный корень уравнения

с точностью до 0,01.

В этом уравнении f(х)=х^4-2x-4, f`(х)=4х^3-2,а f«(х)=12x^2.Так как f(х) и f«(х) при х0 = 1,7 имеют один и тот же знак, а именно:

f(1,7)=0,952>0 и f«(1,7)>0, то применяем формулу:

x1`= х0- f(х0)/ f`( х0), где f`(1,7)=4*1,7^3-2=17,652. Тогда

Применяем второй раз способ касательных:

х2= x1- f(x1)/ f` (x1), где f(x1)= f(1,646)=0,048, f` (1,646) =15,838;

f(1,643)=0,004, f` (1,643)=15,740;

Следовательно, искомый корень с точностью до 0,01 равен 1,64.

1.3 Комбинированный способ

(комбинированное применение способов хорд и касательных).

Этот способ состоит в одновременном использовании способов хорд и касательных. Остановим своё внимание опять на случае, отвечающем первому рисунку №2. Значения x1 и x1`, вычисляем по прежним формулам, т. е. принимаем:

x1`=b-f(b)/f`(b), причём: x1 0 изображён на рисунке №7. Из этого рисунка видно, что уравнение имеет положительный единственный корень, лежащий на отрезке 1 0,f«(x)>0 т. е. знак производных сохраняется. Применяем комбинированный способ:

Формулы (10) дают:

При этом x1`- x1=0,012, т. е. точность недостаточна. Совершаем второй шаг:

При этом х2`- х2=0,00018, т. е. точность достаточна. Таким образом:

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

К вопросу о приближенных методах решения уравнений третьей степени Текст научной статьи по специальности « Математика»

Похожие темы научных работ по математике , автор научной работы — Бетехин Александр Сергеевич

Текст научной работы на тему «К вопросу о приближенных методах решения уравнений третьей степени»

ТОМСКОГО ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ПОЛИТЕХНИЧЕСКОГО Том 67, вып. 2 ИНСТИТУТА имени С. М. КИРОВА 1951 г,

К ВОПРОСУ О ПРИБЛИЖЕННЫХ МЕТОДАХ РЕШЕНИЯ УРАВНЕНИЙ ТРЕТЬЕЙ СТЕПЕНИ

А. С. БЕТЕХТИН Введение

При исследовании некоторых вопросов теоретического и инженерного порядка часто возникает необходимость в решении уравнений третьей степени.

Точное и сравнительно быстрое решение уравнения третьей степени возможно лишь тогда, когда оно путем соответствующих преобразований может быть представлено либо в виде (л; + а)3 = 0, либо в виде (х^а)9 = т, либо, наконец, в виде (х — а1)(х — Ь<)(к — г1)=0. В остальных же случаях приходится довольствоваться приближенными решениями с той или иной степенью точности.

Прежде чем перейти к рассматриваемому вопросу, полезно, хотя бы вкратце, остановиться на общеизвестных методах определения с заданной* степенью точности корней второй и третьей степени, а также корней алгебраических уравнений, так как эти методы в известной степени (главным образом, как контрольные методы) могут быть использованы и в предлагаемом нами методе решения уравнений третьей степени.

Способ извлечения квадратных и кубических корней, открытый индусскими математиками, до конца XVI века был почти неизвестен в Европе Только в конце XVI века через арабов, вероятно, из Испании он проник в Европу. В 1600 году этот метод был развит математиком Виетом, приспособившим его к вычислению корней алгебраических уравнений. Но в том виде, в каком он был предложен Виетом, этот метод на практике оказался настолько трудоемким, что вычисление при помощи его корней алгебраических уравнений один из математиков XVII века назвал „работой, недостойной христианина». Несмотря на это, он все же продержался около 80 лет, примерно до 1680 года.

В 1674 году Грегори и Дари почти одновременно и независимо друг от друга разработали метод определения квадратных корней, названный „принципом итерации». Этот принцип был в дальнейшем разработан Ньютоном и для определения корней алгебраических уравнений.

В применении к извлечению квадратных корней принцип итерации сводится к следующему:

„Пусть имеется число N и требуется найти его квадратный корень. Возьмем некоторое число х0 и составим при его помощи число хи удовлетворяю-

Э. Уиттекер и Р. Робинсон „Математическая обработка результатов наблюдений»

ОНТИ, 1935 г., стр. 77—78.

По х1 составляем также число хг,

удовлетворяющее уравнению х2 =—1^1-1—• По хг составляем уравне-

ние х% — — —) и т. д. Тогда последовательность чисел л*0, хи

2 \ х2/ х3. стремится к пределу ^М»1).

Пример. Найти У\0

Решение Полагая 10 и хп=\, имеем

= ^ (з^ + = (3,7 -Ь 2,7) = 3,2,

= -i- (3,2+ — (3,2 + 3,125) = 3,163,

— (3,163 +— (3,163+ 3,161555) = 3,1622775. 2 \ 3,163 / 2 V ^ ‘ ■

Последнее число и будет j/10 с точностью до 6-го десятичного знака. Нетрудно убедиться, что и при другом значении лг0 будет получен аналогичный результат. Так, при л0 — 2, atj = 3,5, лг2 = 3,18, xs = 3,16 и xt = 3,16228.

Метод Ньютона-Рефсона, предложенный Ньютоном (1685 г.) и Рефсо-ном (1690 г.) для вычисления корней алгебраических уравнений, сводится к следующему.

Если х0, хи хг, х3. —приближенные значения, последовательно стремящиеся к истинному значению корня f(x) = 0, то между х0, xv хг и т. д. должна существовать следующая зависимость:

Пример. Найти положительный корень уравнения л3 — 2х — 5=0. Решение. Первое приближенное значение корня этого уравнения будет, очевидно, = Оно меньше истинного, так как 23 Ьи Ь2 больше истинных значений х, и если последующие значения а, аи а2 и Ь, Ь^ Ьг выражаются через предыдущие так:

то степень точности вычисления х будет определяться числом одинаковых десятичных знаков у а и ft, at и bu ci2 и ft2.

Например, первое приближенное (преуменьшенное) значение корня уравнения Xs — 23,4 х — 8 — 0 будет a

V 23,4 = 4,793, второе — (преувеличенное) ft = у^ 23,4+= 5,006, ft—a = 5,006 — 4,793 = 0/213,

f (а) = — 9,05, f (ft) = + 0,02, ax = 4,793 —■ 0,2131″9»05* = 5,0055, /'(ft) =

= 44,58, fti = 5,006—__ 5 QQgg^ цисло одинаковых десятичных зна-

ков у ах и &t —три, т. е. для данной стадии расчета корень уравнения найден с точностью до тысячных долей. Истинное значение х = 5, ошиб^ ка 0,1%.

Переходя к поставленной нами задаче, следует отметить, что, кроме классического метода Кардана, не всегда дающего правильные решения,1) существует довольно много методов приближенного решения уравнений третьей степени: метод Ньютона, Гресрфе, Энке, „метод ложного поло* жения» и т. д. Имеется даже работа,2) пользуясь которой можно по коэффициентам при неизвестном (считая, что свободный член является коэ-фициентом при х°) найти все три корня уравнения*

Не входя в сравнительную оценку этих методов, укажем лишь, что определение при их помощи значения неизвестного с достаточной степенью точности является довольно громоздким и трудоемким процессом. Что же касается вышеупомянутой работы инж. В. С. Осипова, то она может быть использована для получения значений х, лежащих в определенных, сравнительно узких границах.

Предлагаемые ниже способы приближенного решения уравнений третьей степени, являясь простыми и несложными, позволяют сравнительно легко и быстро определить значение неизвестного с желаемой степенью точности. Они могут быть применены для решения любого вида уравнения третьей степени, если только это уравнение имеет хотя бы один вещественный корень—безразлично, положительный или отрицательный.

4) Военный инженер III ранга В. С. Осипов. Таблицы для решения кубических уравнений. Военно-инженерная академия РККА иденн В. В. Куйбышева, Москва, 1937 г. стр. 3. .

§ 1. Приближенное решение неполного уравнения третьей степени вида

Неполные уравнения третьей степени можно разделить на 8 групп отличающихся друг от друга либо знаками при лил2 при одинаковом знаке у свободного члена, либо знаками у свободного члена при одинаковых знаках у х и х2.

1. л3 — Ьх — с = 0 5. л3 — ах- — с — О

2. х3 —&х + с = 0 6. л3 — ах2 + с — О

3. +Ьх — с = 0 ‘ 7. х* + ах2 —с— О

4. + г = 0 8. х* + ах* + с = 0

Нет необходимости исследовать все 8 групп: уравнение, условно отнесенное нами к четвертой группе, простой заменой с на—с превратится в уравнение третьей группы, а уравнения последних четырех групп могут быть приведены к уравнениям одной из трех первых групп путем замены л

Переходим к решению уравнения, условно отнесенного к первой группе, т. е. уравнения х3—Ьх — с = 0. Пусть имеется уравнение

— Ь\Х -— с — О, Ь, то это будет означать, что значение х=*2г будет больше истинного, так как для компенсации величины хя — с необходимо отнять от нее не Ьх как это требуется уравнением (1а), а 3,5величину больщую, нежели Ьх. Если же 3,5значение х = 2г будет, очевидно, меньше истинного, т. е. будет найдено с недостатком.

Если й—разность между истинным значением х и х1 — равна 2 г, то, подставив в уравнение (1а) вместо х,х+й и решив его- относительно получим величину разницы между х1 и х. При этом величиной ¿3, как слишком малой по сравнению с другими величинами раскрытого уравнения С*1 + — За:,8 й-^-Ъхх Ф — Ф — ЬххА-Ьй — с —О х<А — Ьхх — с = О

3 хг Ф — (3 X!2 — Ь) й + (Ь1 — Ь)хг

01 куда легко определяется й> так как величины х^ Ь и Ьх можно считать швестными.

Если хг Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

деляем си т. е. величину свободного члена, при котором х2 = 2г2 = 2 У сх. Если то А*2 = 2г8 будет меньше истинного, так как для соблюдения

условия х3 — Ьх — ¿7=0 от х3 — Ьх требуется отнять величину с19 меньшую, нежели обусловленную уравнением (1а). В противном случае, т. е, при

В дальнейшем определение разницы между х и х2 производится так же, как и в предыдущем случае.

Пример. Найти вещественный корень уравнения л3 — 23,4л; — 8т=0

Решение. В данном случае 6 = 23,4 и с = 8,

Гак как Ьх то х: с, то х2 > х.

Определяем di из уравнения (х2 — rfi)3 — 23,4 (лг2 — rfj) — 8 = 0, которое, после соответствующих преобразований, примет вид:

Итак, х = х2 — ¿, = 5,17-0,17 = 5,00.

Очевидно, значение х = 5 ближе к истинному, чем х —5,02. Действительно, в первом случае, т. е. при х = 5,02, разница между грубо приближенным значением х = хх = 4 и истинным его значением (5) составляет 20% от истинной величины х, Поэтому пренебрежение величиной дало ошибку на 0,02 или 0,4%. Во втором же случае, т. е. при х —х% = 5,17, — х = 0,17 или 3,4% от величины х, и пренебрежение величиной 0,17* не сказалось на конечном результате. Итак, х = 5,00.

Два других корня заданного уравнения определяются из условия, что

их сумма, взятая с обратным знаком, равна х, а их произведение—,

Короче, говоря, они определятся из квадратного уравнения х2 5х +1,6 = 0, Решение его дает:

х’ = — 2,5 + /6,25—1,6 = — 2,5 + = — 0,34,

х* = — 2,5 — \/ 4,65 = — 2,5 — 2,16 = — 4,66.

§ 2. Приближенное решение уравнения вида

Найдем значения коэфициента при х или свободного члена, при кото-

рых будет соблюдено условие хх = 2 ги = 2 |/У или х2 = 2г2 = УИ£

Приняв в общем случае х = 2г = 2 Ус, будем иметь: 8г’л — Ь.2г = о,

Из последнего уравнения получаем, заменив с искомым с2:

В остальном методика решения рассматриваемого уравнения остается такой же, как и в случае уравнения х3— Ьх-с — 0. Пример. Найти корни уравнения хг — 42*+ 36 = 0. Решение (первый вариант). Находим значение коэфицйента Ьи при

Так как Ьх > Ь, то = 2 У с будет больше истинного. Находим 2Х =

= >/36 = 3,302 и х1 = 2г1 = 6,604.

Определяем разность между хх и х из выражения (4):

¿г-4,484 ^2,353 = 0, откуда

= 2,242— 5,024—2,353 =2,242-1,634 = 0,608. Итак, Л! =6,604 — 0,608 = 5,996.

Второй вариант. Находим значение сгл при котором л*2 = 2|/»с^:

>= у71^28,52 и л2 — 2 |/ 28,52 = 2-3,055 = 6,11.

Так как для соблюдения условия х3—42 х + 36 = 0 при лг2 = 6, 11 —х к х3 —42 х надо прибавить не 36, а только 28,52, величину меньшую с, то, очевидно, х2 тоже больше х.

Находим разность между и предполагаемым истинным значением х, для чего пользуемся уравнением

полученным путем совместного решения уравнений

В рассматриваемом — случае х2 = 6,-11, 6 = 42, с =36 и с2 =28,52, и уравнение (8) примет вид:

I п 11 ** \ ^ г —¿ОуОг Л

(Ръ—3,8194, + 0,4081 =0, откуда

¿.« 1,9095— 1/ 3,6475-0,4081 =1,9095-1,7999=0,1096.

Отсюда х = 6,И —0,1096 = 6,0004.

Итак, х лежит в пределах 5,996 6,0004.

Так как в первом варианте относительная ошибка, равная 0,608, почти в 6 раз больше, чем во втором, то наиболее близким к истинному значению будет 6,0004. Действительное значение х будет 6,0, в чем нетрудно убедиться, подставив это значение в уравнение л:3—42-«->- 36 ==г 0. Но даже значение х, полученное при первом варианте, отличается от истинного всего на 0,004 или на 0,066%. Это точность, вполне достаточная для технических расчетов.

Можно было бы, конечно, не прибегать ко второму варианту, а уточнить полученное при первом варианте значение л:, применив метод Ньютона-Рефсона. Тогда получили бы: /(*) = — 0,265, /'(*) — 65,855 и

л-у = 5,996 -I—0,265 = 5,996 4- 0,00402.

Итак, х = 6,00002. Очевидно, для расчетов было бы принято значение х = 6,0.

Другие корни уравнения определятся из уравнения х*-\-6х—6 = 0, которое получится, если хг—42х->-36 = 0 разделить на х—6. Эти корни бу-дут: х’ = — 3 + У1Ь и х» = — 3 — К15.

§ 3. Приближенное решение уравнения вида

В данном случае было бы нецелесообразно принимать х1=2]/

^ п0. скольку с компенсирует х3-\-Ьх\ поэтому значение хх получилось бы очень преувеличенным, и точность решения была бы невелика, так как раз-

тзость хх—х получилась бы со значительной ошибкой. В этих условиях

правильнее принять коэфициент при У с не 2, а. меньше 1, например, ОД т. е. принять

Тогда уравнение х] Ьх—с — 0 примет вид:

0,729г! +0,96^—^ = 0. тдег=1/ с

Из предыдущего уравнения следует, что для соблюдения условия

^=0,9Ус необходимо, чтобы

Итак, Ъх = 0,3^2 или более точно Ьх = 0,3011 £2. Если Ъх > Ь, то хх ж; 2) либо

определяются с2 и х2 = 0,9 ]/с2 и тоже находится разность ¿¿2 из выражения

причем знак4-У коэфициента при йг берется при а знак минус —

и противоположном случае.

Пример. Решить уравнение х*-\-5х—84 = 0.

Р е ш е н и е (первый вариант). Определяем Ьх и хх:

Ьг — 0,301122, или _ о,3011 У%А2 = 5,7753.

^ = /84 = 4,38 и л-! = 0,9.4,38 = 3,942. Так как Ьл > то хх __

йх — — 2,180 + /4,7520 + 0,2584 = — 2,180 + 2,238 = 0,058. Значение х будет: 3,942 + 0,058 = 4,000.

Второй вариант решения. Определяем с2, при котором

22 = Уб7,668 = 4,075, х2 — 0,9.4,075 = 3,6675.

Так как то х2 или Ъ% = 0,3011.112,92 = 34,0; о>

сюда = 0,9/1200 = 10,627.0,9 = 9,5643. Так как Ьх > Ь, то хх а х9 при аг х Можно также определить

затем хг = 2\Гс^ ъ9 наконец, поправку й2 из уравнения;

Знак + у коэфициента при й2 в случае х2 х в том слу^е,-е?ди с2> с. Пример. Найти положительный корень уравнения л;3— 11 л:2-— 1 44 = 0. Решение. Не приводя подробных вычислений, укажем лишь значения х, полученные при решении .этого уравненяя по первому « второму вариантам. .

1) = Ущ = 5,2415 = 2г = 10,483;

¿2 = 0,573 (из уравнения 18) и л: = 12,571—0,573 = 11,998.

Итак, х лежит в пределах 12,007-^-11,998. Нетрудно убедиться, что щетинное значение х будет 12. Наибольшая ошибка равна 0,007 или 0,06%.

Решим это же уравнение, заменив в нем х через В общем случае

уравнение х:1 — ах2 — ¿ = 0 после преобразования примет вид:

Применительно к данному примеру будем иметь:

V3 —»40,333 у — 242,6 = 0

Решение его дает: гх = /242,6 = 6,2367; Ъх = 3,5/242,б2 —136,14;

^=-.2^1 = 12,4734. Поправка йх (учитывая, что ух>у, так как ЬХ>Ь)= __4,990; у =12,4734 — 4,990 = 7,463; х = 7,463+-3,666= 11,129.

Ошибка равна 12,000—11,129 = 0,871 или 7,26%, т. е. во много раз €юльн&, при котором, при коэфициенте а, бу

дет соблюдено условие х^—2Усъ определится соотношением:

Вообще! же это уравнение решается аналогично предыдущему, причем поправки йх и й2 определяются из тех же уравнений, что и в предыдущем случае. Только в уравнении для й% знак перед свободным членок должен быть изменен на обратный.

Пример. Найти положительный корень уравнения л3— 13л2 + 242 = О.

Решени е(первыйвариант).^ = К242 =6,2317; хх = 2^= 12,4634;ах-=

= 14,021; а*>а —значит ¿^ = 1,510; л; = 12,463 —1,510 =

Второй вариант: = 5,7777;л2==2;г2^И,555;

съ Т ) — 192,9; с2 х;

й2 = 0,558; х = 11,555—0,558 = 10,997.

Истинное значение л = 11,0. Таким образом, ошибка в определении х лежит в пределах 0,047-н0,003 или в процентах 0,043—0,03%. Ошибка может быть еще уменьшена, если уточнить любое из найденных значений л,, пользуясь правилом Ньютона-Рефсона.

Определим х, приведя заданное уравнение к виду х’6 — Ьх-^с — 0.

Пусть х = у —значит

Поправка йх = 2,0397 найдется из уравнения

— ( 8,5912 — 56’3333 )^ + 83’°32-56’331 = 0 . \ 3.8,5912 > 3

Тогда у — 8,5912 — 2,0397 = 6,5515

и х = 5515 + 4,3333= 10,8848.

Истинное значение х, как уже указывалось выше, равно 11. Ошибка равна 11,0000—10,8848 = 0,1152 или около 1,05%. Таким образом и в атои^слу-чае решение уравнения, приведенного к виду хъ-

Ьх-\-с=. 0, [дает меньшую точность, нежели непосредственное решение уравнения

§ 7. Приближенное решение уравнения вида

Обозначив х через у — —, получим преобразованное уравнение в виде МЛН y* — bv±Ci = 0,

Затем преобразованное уравнение решаем по одному из способов, рас« мотренных выше. Но возможен и другой путь решения. Так как в данном уравнении х3 и ах2 имеют одинаковые знаки, та

X Примем jc = x1 = 0,8|/»^»1). Очевидно, в эти*1условиях коэфи» диент при х2 будет уже не равен а. Значение ко^фициента аи удовлетво*

ряющее рассматриваемому уравнению при хх = 0,8|/Т

^ определится из урав» зения:

Xi3 4-aiX, — с = 0, или 11

а и минус—при ах Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Уравнения этого вида не имеют положительных корней. Изменив на обратный знак у йечетной степени, получим уравнение л3 — ах2 — с = 0, уже расСйбФренное ракее. Цайдённый при решении этого уравнения пала» ^к^тельный корень надо взять с обратным знаком. Прймер. Найти корень уравнения х3 +’2,5 х2 4е 4,5 = 0.

Решение. Представляем данное уравнение в виде: х3 — 2,5л2 — 4,5.=№..

Примем хх = 2 1^4 5 = 2.1,651 =3,302. Согласно предыдущему (§5), ат =

= — — 7.1,651 _ 2,889. Так как ах > а, то хг больше истинного эначе

Поправку йх находим из выражения (16):

2-2’5) ^ | 1 точность самой поправки становится сомнительной! так как в эпш случае пренебрежение величиной (Р дает значительную ошибку при ои-

ределении й. Поэтому рациональнее прийймать х равным не 2\г’с

огя подобное допущение в пот^ебуе’т-ре^ення

уравнения третьей степени относительной. ^Действительно,7 йуст^; например, имеется уравнение х3— ¿>х —г = 0« Подставное него вместо х

т Vс и разделим все члены на с. Получим; т%с Ьту с__^ — о

Решение уравнения (24) проще, чем исходного, из которого оно получено..

» • • 1 В самом деле, представив уравнение (24) в виде /я2 = &Н—,

и рассматривая правую часть выражения (25), как бином, получим, ограничившись двумя членами бинома:

т — ЬЧъ-А—Ь 3 = 1/7?. —Г7=>

1 ^ 2 т ¥ 1 2тУьх

т* — тУ Ъх — —т^г = 0 (26)

Таким образом, приближенное решение кубического уравнения (24) сведется к решению квадратного уравнения (26)

Нетрудно убедиться, что знак перед корнем в числителе выражения (27в-^доя|кен«.6ы» как Щ ^ цошт быть отрицательным числом.

Пример. Решим данным методом уравнение

—23,4 х —8=== 0, уже решенное в§ 1.

Преобразованное уравнение примет вид:

тА — -23;4 т — 1 = 0, или тА — 5,85 т —1 = 0. —

В этом уравнении ¿>1 = 5,85,

5,85+^85^2^5^5 = 5,85 + ^34,2225 + 2,2,4187 2У

_ 5,85+V’39,0599 _ 5,85 + 6,250 _ Щ10 —

или 771 —— —г1^—;—;—:—■• ■ ■ -1 ‘ —— ди,

Так как лг = т|/Т>. то 8 данном случае х = 2,5У$ = 5,0, что и является истинным корнем рассматриваемого уравнения, В § 1 для х было полу- * чено значение 5,02, т. е. с ошибкой 0,4%.

Следует отметить, однако, что степень точности определения величины т из выражений (27) и (27а) в значительной мере зависит от абсолютной величины как это можно видеть из табл. 1.

Истинные значения т и вычисленные из выражения (27), как функции Ь1

вычисленные из Д т Дот в Н

истинные выражения (27)

0,309 1.1 1,2660 0,1660 15,10 ,

0,607 1,2 1.2804 0,0804 6,70

0,921 1.3 1,347 0,047 3,62

1,246 М 1,4296 0,0296 2,12

1,583 1.5 1,5186 0,0186 1,24

1,935 1.6 1,6136 0,0136 0,85

2 »302 1,7 1,7099 0,0099 0,58

2,684 ».8 1,8072 0,0072 0,40

3,084 1,9 1,90.^7 0,0057 0,30

3,500 2.0 2,0042 0,0042 0,21

3,934 2,1 2,1036 0,0036 0,17

4,385 2.2 2,2029 0,0029 0,13

5,343 2,4 2,4012 0,0012 0,05

С возрастанием Ьх растет и значение т и одновременно уменьшается расхождение между истинным и вычисленными значениями т. Действительно, из выражения т

следУет> 4X0 с в03Рас*

танием Ьх влияние его на величину подкоренного количества будет умень» шаться, и т будет приближаться к Это, впрочем, ясно и из урав-

нения т* — Ьхт —1=0: при достаточно большой величине Так, при &| = 100, разница между истинным и приближенными значениями т будет всего —-— (или 0,00345), т. е. всего 0,0345%. Другими ело-, , « 290

вами — при ¿>1>2,5 выражение (27) дает вполне достаточные для практики результаты.

Для уравнения вида х* — Ьх-\-с — 0 значение т получится из выражения, аналогичного выражению (27), а именно:

В табл. 2 приведены значения т истинные и вычисленные по формуле

(28), а также величина ошибки абсолютная и в процентах, т. е. т (истинные).

• Таблица 2 Истинные значения т и вычисленные по формуле (28), как функции

.Значения Ь. истинные вычисленные из Д т Дт в Н

2,1192 1,1 1,1646 0,0646 +5,87

2,733 1,2 1,2537 0,0537 4,46

2,4592 1.3 1,3282 0,0282 2,19

2,6743 1.4 1,4192 0,0192 1,37

2,9133 1,5 1,5135 0,0135 0,90

3,1850 1.6 1,6110 0,0110 0,69

3,4782 1,7 1,7083 0,0083 0,50

3,7944 1,8 1,8055 0,0055 0,31

4,1363 1,9 1,9047 0,0047 0,24

4,5000 2,0 2,0036 0,0036 0,18

5,2945 2,2031 0,0031 014

6,1766 2,4 2,4025 0,0025 0,10

6,6500 2,5 2,5013 ■ 0,0013 0,№2

Определив Ьх из выражения Ьх = ^

можно, пользуясь табл. 1 и

2 (в зависимости от типа уравнения), найти ближайшее значение т9 соответствующее найденному значению Ьх. Более же точно значение т можно найти следующим образом: решив уравнение (27) или (28), из табл. 1 или 2 находят границы, между которыми лежит т. Если, например, для уравнения тъ — Ьхт-\-\ = 0 получилось /«=1,55, то из табл. 2 видно, что возможная ошибка лежит в лределах 0,9-н-0,6994. В данном случае

она будет порядка 0,78%. Разделив найденное значение т на 1 + ,

получим значение, отличающееся от истинного на сотые доли процента, что более чем достаточно при решении технических вопросов. Например, при определении состава электровоза, допустимого нагревания электровозных двигателей, подобная точность даже излишня, так как погрешность в 1% является здесь вполне допустимой. . Для решения уравнения вида тъ-^-Ьхт—1=0 нельзя воспользоваться

уравнениями (27) или (28), так как выражение т2 = /Г—-

в конечном* счете все равно приводит к уравнению

третьей степени. Поэтому т приходится определять приближенно, поль зуясь табл. 3.

Значение т, как функции Ьх

0,05 19,9975 0,55 1,5157

0,075 13,3244 0,60 1,3066

0,10 9,9900 0,65 1,1160

0,15 6,6441 0,70 0,93«6

0,20 4,9600 0,75 0,7708

0,25 3,9375 0,80 0,6100

0,30 3,2433 0,85 0,4565

0,35 2,7346 0,90 0,3011

0,40 2,3400 0,95 0,1501

0,45. ‘ 2,01*07 1,00 0,0000

Если, »¿пример, Ьи найденное из уравнения Ьх — -, равно 3, то т

можно, принять равным

__ (3,0000 — 2,7346)0,05 = 0Д)26 = ^

§ 10. Решение полных уравнений третьей степени

Решение полного уравнения третьей степени может быть сведено к трем этапам: 1) превращение полного уравнения в неполное путем заме

ны х через у+—; 2) превращение полученного неполного уравнения 3

в уравнение вида т? — Ьхт — 1=0, /п3 — Ьхт +1=0 или т? + Ьхт— 1=0;

3) решение полученного уравнения относительно т и определение

Пример. Найти положительный корень уравнения

х3 — 6 лг2+ 10 х — 8 = 0.

-Если обозначить л: через у-\-% то данное уравнение можно предста вить в виде .у3 — 2у — 4 = 0, т. е. в виде уравнения, условно отнесенного

н I тпу. (Обозначив у —ту 4 и подставив это значение в полученное уравнение, будем иметь:

т] — 0,7937 т — 1=0, где 0,7937 = Ъх.

Г’В^ дальнейшем полученное уравнение можно решать либо по формуле (¿7),г-?лвбо. пользуясь табл. 1, найти т, соответствующее найденному зна-чению ^ Ввиду малого значения Ьи возможная величина ошибки при пользовании уравнением (27) окажется очень значительной, лежащей в пределах *6|7 -ь-3,62%. Поэтому лучше найти \м изтабл. 1 путем интерполирования! хотя , и в этом случае неизбежна ошибка, но значительно меньшая* чем при определении т из уравнения (27). Для рассматриваемого примера

ОТ== 1,2 4- ^7^070^ = 1,2+0,059- 1)26. 0,921 — 0,607

Тогда у = 1,26уг_4

= 2,0001. Примем у = 2. Тогда х=у + 2 = 4. Проверка полученного значения х по формуле Ныотона-Рефсоца дает для /(х) значение 0, что означает, что поправка равна нулю и значение получено с абсолютной точностью. Аналогично решаются полные уравнения третьей степени, приводимые к виду у* — 6у + с=0 или уг-\-Ьу — с = 0. В первом случае т определяется либо из уравнения (28), либо из табл. 2; во втором случае —из табл. 3, с последующей проверкой по формуле Ньютона-Рефсона.

1- Неполные уравнение третьей стеаени могут быть условно разделе-ны на 8 групп, котбрые в конечном счете могут быть сведены к 3 основным группам.

2. Решение уравнений 2 первых групп сводится к определению^ приближенного значения неизвестного, условно принимаемого равным удвоенному кубичному корню из. свободного члена, и отысканию поправки^ определяемой из уравнений.

3. При решении уравнений 3-ей группы условное значение неизвестного принимается равным 0,7-^-0,9 кубичных корней из свободного члена.

Величййа коэффициента переду^выбйрается такой, при которой разница между коэфициёнтами Ь и Ъх будет минимальной. ‘

4. Неполные кубическре, уравадн&я, , содержащие х2, могут быть решены либо методом, аналогичным методу, предложенному для решения первых трех групп уравнений, либо приведены к одной из этих групп

путем замены х через у —

В первом случде сложнее определение величины поправки но выше точность.

5. Вместо условного значения х = 2у с целесообразнее принимать

х=т у с • Величина т для первых двух групп уравнений определяется из выражений___

т=УА-+,/кгг» или т=^+, /»¿1 _ х:

2 V 4 Гьх 2 у 4 2 уь\\

причем, если Ь> 3,5, ошибка не превысит >0,5%-* В противном случае, найденное значение т необходимо уточнить либо с помощью фррмулы Ньюто-на-Рефсона,л и бос помощью табл. 1 и 2.

Для уравнений третьей груяпы величина т определяется из табл., 3 путем интерполирования, соответствеяно коэфициенту ,

Уравнения, содержащие х\ предварительно приводятся к уравнениям первых трех групп, длр которых определение величины- т указано выше

6. Предлагаемые два; способа приближениях решений Надоели баннеры? Вы всегда можете отключить рекламу.

Приближенное решение уравнений в электронных таблицах

Тип урока: Изучение и закрепление новых знаний.

Вид занятия: практическая работа с использованием компьютера.

Продолжительность занятия: два урока.

Цель: Научиться решать уравнения с заданной точностью на заданном отрезке.

• развитие исследовательской, познавательной деятельности учащихся;
• развитие умений использовать различные программные средства при решении одной задачи;
• развитие коммуникативных способностей учащихся.

Методы обучения: наглядный, исследовательский, практический.

1. Операционная система Windows;
2. Microsoft Excel из пакета Microsoft Office;
3. Microsoft Visual Basic 6.0.

1. Организационный момент.
2. Создание проблемной ситуации.
3. Использование графического метода для приближенного решения уравнений в электронных таблицах.
4. Изучение метода половинного деления при решении уравнений.
5. Моделирование листа электронных таблиц для приближенного решения уравнения методом половинного деления.
6. Моделирование проекта “Приближенное решение уравнения” на объектно-ориентированном языке Visual Basic 6.0.
7. Компьютерный эксперимент.
8. Анализ полученных результатов.
9. Подведение итогов урока.

1. Организационный момент.

2. Создание проблемной ситуации.

– Сегодня нам предстоит решить задачу нахождения приближенного корня уравнения cos(x)=x, используя различные программные средства. Запишите тему урока: “Приближенное решение уравнений разными инструментальными средствами.”

– Пока вы не знаете никаких математических приемов решения этого уравнения, но знаете программу, в которой можно приближенно решить его графическим способом. Какая это программа? (Microsoft Excel.)

3. Использование графического метода для приближенного решения уравнений в электронных таблицах.

– В чем смысл метода? (Нужно построить график функции y = cos(x)–x на некотором отрезке, абсцисса точки пересечения графика с осью OX является корнем уравнения cos(x)=x.)

– Что нужно определить для построения графика? (Отрезок, на котором существует корень.)

– Сделайте это математическим методом. (Множеством значений левой части уравнения, функции y = cos(x), является отрезок [-1; 1]. Поэтому уравнение может иметь корень только на этом отрезке.)

– Итак, найдите приближенный корень уравнения cos(x)=x на отрезке [-1; 1] с шагом, например, 0,1 в программе Microsoft Excel.

– Приближенный корень уравнения х=0,75. Однако это приближение не обладает высокой точностью. Для нахождения приближенного корня уравнения с указанной заранее точностью используются математические методы, в частности, метод половинного деления.

4. Изучение метода половинного деления при решении уравнений.

Рассмотрим непрерывную функцию f(х), такую, что корень данного уравнения является точкой пересечения графика этой функции с осью ОХ.

Идея метода половинного деления состоит в сведении первоначального отрезка [а; b], на котором существует корень уравнения, к отрезку заданной точности h.

Процесс сводится к последовательному делению отрезка пополам точкой с=(а+b)/2 и отбрасыванию половины отрезка ([a; c] или [c; b]), на которой корня нет. Выбирается тот отрезок, на концах которого функция принимает значения разных знаков, т.е. произведение этих значений отрицательно. Функция на этом отрезке пересекает ось абсцисс. Концам этого отрезка вновь присваивают обозначения a, b.

Это деление продолжается до тех пор, пока длина отрезка не станет меньше удвоенной точности, т.е. пока не выполнится неравенство (b-a)/2 = e

Практическая работа

Приближенное решение уравнений

Просмотр содержимого документа
«Практическая работа Приближенное решение уравнений»

Приближенное решение уравнений

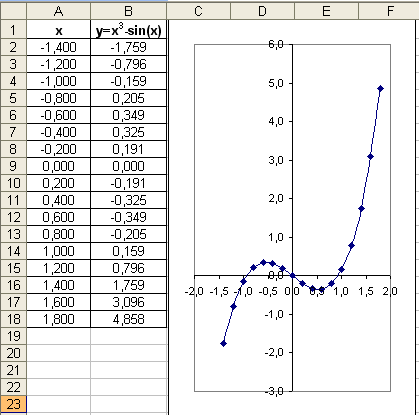
Создать компьютерную модель «Приближенное решение уравнений» с использованием электронных таблиц Microsoft Excel, которая позволяет найти корень уравнения x 3 = sin x приближенными методами (графическим и с помощью метода Подбор параметра).

Представить функцию в табличной форме, построить ее график, который позволит определить корни уравнения грубо приблизительно.

Представить заданное уравнение в табличной форме.

Для грубо приближенного определения корня построить диаграмму типа график. По графику грубо приближенно можно определить, что х=0,8.

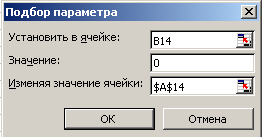
Для поиска решения с заданной точностью используем метод Подбор параметра. Точность подбора зависит от заданной точности представления чисел в ячейках таблицы (например, до трех знаков после запятой). Методом подбора параметра необходимо определить значение аргумента х (ячейка В14) равно нулю.

Выделить ячейку со значением функции В14 и ввести команду [Сервис-Подбор параметра…].

На панели Подбор параметра в поле Значение ввести требуемое значение функции (в данном случае 0).

В поле Изменяя значение ячейки ввести адрес ячейки $А$14, в которой будет производиться подбор значения аргумента, и щелкнуть по кнопке ОК.

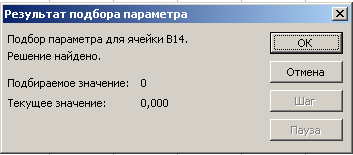
На панели Результат подбора параметра будет выведена информация а величине подбираемого и подобранного значений.

В ячейке аргумента А14 появится подобранное значение 0,929. Таким образом, корень уравнения х=0,929 найден с заданной точностью.

Аналогично определите второй корень уравнения.

Задание для самостоятельной работы. Создать компьютерную модель «Приближенное решение уравнений» с использованием электронных таблиц Microsoft Excel, которая позволяет найти корень уравнения х 3 = sin х графическим способом.

Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .

Описание презентации по отдельным слайдам:

Приближенное решение уравнений c помощью электронных таблиц MS EXСEL

1 способ графического решения уравнений с одним неизвестным Пусть дано уравнение f(x)=g(x). Приведем это уравнение к виду f(x)-g(x)=0 Введем функцию у=f(x)-g(x). Построим график этой функции Количество точек пересечения графика с осью абсцисс дает число корней уравнения Абсциссы точек пересечения и есть решения данного уравнения

2 способ графического решения уравнений с одним неизвестным Пусть дано уравнение f(x)=g(x). Введем функции у= f(x) и у =g(x). Построим графики этих функций в одной системе координат. Количество точек пересечения дает число корней уравнения. Абсциссы точек пересечения и есть решения данного уравнения.

Алгоритм использования команды Подбор параметра: Решить нужную задачу с каким – либо начальным значение параметра; Выбрать команду Подбор параметра в меню Сервис; В появившемся окне диалога Подбор параметра в поле Установить в ячейке указывается адрес ячейки, значение в которой нужно изменить (такая ячейка называется целевой); В поле Значение – то числовое значение, которое должно появиться в целевой ячейке; В поле Изменяя значение ячейки ввести ссылку на ячейку с параметром

Использование надстройки Подбор параметра для 1 способа По графику видно, что ближайший аргумент к точке пересечения оси Х с графиком функции равен -1,1. По таблице значений функции можно определить, что этот аргумент функции хранится в ячейке А5 Выделить ячейку В5 со значением функции и выполним команду Сервис-Подбор параметра…. В диалоговом окне в поле Значение: ввести требуемое значение функции (0). В поле Изменяя значение ячейки: ввести адрес $A$5, в который будет производится подбор значения аргумента. Кнопка ОК В ячейке аргумента A5 появится подобранное значение – 1,296. Корень уравнения найден с заданной точностью.

Графическое решение систем уравнений с двумя неизвестными Пусть дана система уравнений f(x,y)=0 и y(x,y)=0 1. Рассмотрим каждое из них в виде y=f(x) и y=u(x); 2. Построим эти кривые на одном графике; 3. Определим координаты точек их пересечения, что будет являться решением исходной системы уравнений.

х1≈-0,5 у1≈5 х2≈1,5 у2≈5

Домашнее задание: 1. § 1.3.4 Н.Д.Угринович «Информатика и ИКТ» 11 класс – вопросы 1,2 2. Практическое задание: решить графически систему уравнений

Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .

1 способ графического решения уравнений с одним неизвестным

Пусть дано уравнение

Приведем это уравнение к виду f(x) — g(x) =0 Введем функцию у= f ( x )- g ( x ). Построим график этой функции Количество точек пересечения графика с осью абсцисс дает число корней уравнения

Абсциссы точек пересечения и есть решения данного уравнения 2 способ графического решения уравнений с одним неизвестным

Пусть дано уравнение f(x)=g(x) .

Введем функции у= f ( x ) и у = g ( x ). Построим графики этих функций в одной системе координат. Количество точек пересечения дает число корней уравнения. Абсциссы точек пересечения и есть решения данного уравнения.

• Барсуков Сергей ВладимировичНаписать 1577 16.01.2015

Номер материала: 306027

Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .

16.01.2015 2520

16.01.2015 1574

16.01.2015 784

16.01.2015 489

16.01.2015 383

16.01.2015 572

16.01.2015 647

Не нашли то что искали?

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.