Приближенное решение уравнений на компьютере

Приближенное решение уравнений разными инструментальными средствами

Тип урока: Изучение и закрепление новых знаний.

Вид занятия: практическая работа с использованием компьютера.

Продолжительность занятия: два урока.

Цель: Научиться решать уравнения с заданной точностью на заданном отрезке.

Задачи:

развитие исследовательской, познавательной деятельности учащихся;
развитие умений использовать различные программные средства при решении одной задачи;
развитие коммуникативных способностей учащихся.

Методы обучения: наглядный, исследовательский, практический.

Оборудование:

компьютер;
локальная сеть;
проектор.

Программное обеспечение:

Операционная система Windows;
Microsoft Excel из пакета Microsoft Office;
Microsoft Visual Basic 6.0.

План урока:

Организационный момент.
Создание проблемной ситуации.
Использование графического метода для приближенного решения уравнений в электронных таблицах.
Изучение метода половинного деления при решении уравнений.
Моделирование листа электронных таблиц для приближенного решения уравнения методом половинного деления.
Моделирование проекта “Приближенное решение уравнения” на объектно-ориентированном языке Visual Basic 6.0.
Компьютерный эксперимент.
Анализ полученных результатов.
Подведение итогов урока.

1. Организационный момент.

2. Создание проблемной ситуации.

– Сегодня нам предстоит решить задачу нахождения приближенного корня уравнения cos(x)=x, используя различные программные средства. Запишите тему урока: “Приближенное решение уравнений разными инструментальными средствами.”

– Пока вы не знаете никаких математических приемов решения этого уравнения, но знаете программу, в которой можно приближенно решить его графическим способом. Какая это программа? (Microsoft Excel.)

3. Использование графического метода для приближенного решения уравнений в электронных таблицах.

– В чем смысл метода? (Нужно построить график функции y = cos(x)–x на некотором отрезке, абсцисса точки пересечения графика с осью OX является корнем уравнения cos(x)=x.)

– Что нужно определить для построения графика? (Отрезок, на котором существует корень.)

– Сделайте это математическим методом. (Множеством значений левой части уравнения, функции y = cos(x), является отрезок [-1; 1]. Поэтому уравнение может иметь корень только на этом отрезке.)

– Итак, найдите приближенный корень уравнения cos(x)=x на отрезке [-1; 1] с шагом, например, 0,1 в программе Microsoft Excel.

– Приближенный корень уравнения х=0,75. Однако это приближение не обладает высокой точностью. Для нахождения приближенного корня уравнения с указанной заранее точностью используются математические методы, в частности, метод половинного деления.

4. Изучение метода половинного деления при решении уравнений.

Рассмотрим непрерывную функцию f(х), такую, что корень данного уравнения является точкой пересечения графика этой функции с осью ОХ.

Идея метода половинного деления состоит в сведении первоначального отрезка [а; b], на котором существует корень уравнения, к отрезку заданной точности h.

Процесс сводится к последовательному делению отрезка пополам точкой с=(а+b)/2 и отбрасыванию половины отрезка ([a; c] или [c; b]), на которой корня нет. Выбирается тот отрезок, на концах которого функция принимает значения разных знаков, т.е. произведение этих значений отрицательно. Функция на этом отрезке пересекает ось абсцисс. Концам этого отрезка вновь присваивают обозначения a, b.

Это деление продолжается до тех пор, пока длина отрезка не станет меньше удвоенной точности, т.е. пока не выполнится неравенство (b-a)/2 = e

«Приближенное решение уравнений на языке Visual Basic».

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Приближенное решение квадратных уравнений на языке Visual Basic».

Цель работы – познакомиться с языками программирования, разработкой и исследованием моделей на компьютере.

На языке алгебры формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований алгебраических выражений, позволяющих выразить переменную величину с помощью формулы.

Для большинства уравнений приходится использовать методы приближенного решения с заданной точностью

Основные этапы работы:

• знакомство с языками программирования;

• знакомство с методами решения математических задач в программе Excel;

• содержательная постановка задачи;

Написанную программу планируется использовать на уроках математики в качестве учебного пособия.

Точные решения существуют только для некоторых уравнений определенного вида (линейные, квадратные, тригонометрические и др.), поэтому для большинства уравнений приходится использовать методы приближенного решения с заданной точностью (графические или численные).

Например, нельзя найти корень уравнения х3- cosx =0 путем равносильных алгебраических преобразований. Однако такие уравнения можно решать приближенно графическими и численными методами

Численные методы решения нелинейных уравнений.

1.1. Постановка задачи.

Пусть имеется уравнение вида

где f (x) — заданная алгебраическая или трансцендентная функция. ( Функция называется алгебраической , если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций — показательная, логарифмическая, тригонометрические, обратные тригонометрические.)

Решить уравнение — значит найти все его корни, то есть те значения x , которые обращают уравнение в тождество, или доказать, что корней нет.

Если алгебраическое или трансцендентное уравнение достаточно сложно, то довольно редко удается точно найти его корни. Кроме того, в некоторых случаях уравнение может содержать коэффициенты, известные лишь приблизительно, поэтому сама задача о точном нахождении корней теряет смысл. В таких случаях применяют численные (приближенные) методы решения.

Поставим задачу найти такое приближенное значение корня x _пр , которое мало отличается от точного значения корня x *, так что выполняется неравенство │ x* – x _пр │  , где  (эпсилон) – малая положительная величина – допустимая ошибка, которую мы можем заранее задать по своему усмотрению. Если корень найден с точностью  , то принято писать x * = x _пр ±  .

Будем предполагать, что уравнение (1) имеет лишь изолированные корни, т.е. для каждого корня существует окрестность, не содержащая других корней этого уравнения.

1.2. Этапы приближенного решения нелинейных уравнений.

Приближенное решение уравнения состоит из двух этапов:

Отделение корней , то есть нахождение интервалов из области определения функции f (x) , в каждом из которых содержится только один корень уравнения (1).

Уточнение корней до заданной точности.

Отделение корней можно проводить графически и аналитически.

Для того чтобы графически отделить корни уравнения (1), необходимо построить график функции . Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения (рис. 1).

ис. 1. Графическое отделение корней (1-ый способ).

На практике же бывает удобнее заменить уравнение (1) равносильным ему уравнением

, (2)

где и — более простые функции, чем . Абсциссы точек пересечения графиков функций и дают корни уравнения (2), а значит и исходного уравнения (1) (рис.2).

Рис 2. Графическое отделение корней (2-ой способ).

Пример 1. Отделить графически корень уравнения .

Решение. Для решения задачи построим график функции (рис. 3).

Рис. 3. График функции .

Из рисунка видно, что один из корней уравнения принадлежит отрезку , второй – отрезку . Так как рассматриваемое уравнение имеет третью степень, то должен существовать еще один корень на интервале .

Пример 2. Отделить графически корень уравнения .

Р
ешение. Преобразуем уравнение к виду и построим графики функций и (рис. 4).

Рис. 4. Графическое отделение корней.

Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку .

Аналитическое отделение корней основано на следующих теоремах.

Теорема 1. Если непрерывная функция принимает на концах отрезка значения разных знаков, т.е. , то на этом отрезке содержится по крайней мере один корень уравнения (1) (рис. 5).

Рис. 5. Существование корня на отрезке.

Теорема 2. Если непрерывная на отрезке функция принимает на концах отрезка значения разных знаков, а производная сохраняет знак внутри отрезка , то внутри отрезка существует единственный корень уравнения f (x) = 0 (рис. 6).

Рис. 6. Существование единственного корня на отрезке.

Пример 3. Подтвердить аналитически правильность нахождения отрезка изоляции корня уравнения .

Решение. Для отрезка имеем: ; Значит, . Следовательно, корень отделён правильно.

Уточнение корней до заданной точности заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Наиболее распространенными являются метод деления отрезка пополам , метод касательных (Ньютона), метод секущих (хорд) .

1.3. Уточнение корней методом деления отрезка пополам.

Метод деления отрезка пополам имеет другие названия: метод половинного деления, метод дихотомии, метод проб, метод бисекций.

Пусть корень уравнения f (x) = 0 отделен на отрезке , т.е. .

Алгоритм приближенного вычисления корня методом половинного деления.

ε – требуемая точность;

a , b – границы заданного интервала (границы поиска корня).

Результат: x _пр – приближенный корень уравнения f (x) = 0.

Шаг 1. Выбрать середину отрезка в качестве приближенного корня.

Шаг 2. Если , то c – искомый корень уравнения, на этом прекращаем вычисления. В противном случае перейти к шагу 3.

Шаг 3. Точный корень уравнения x * отличается от c не более чем на половину длины отрезка, т.е. не более чем на (полученная точность). Проверяем условие . Если условие не выполняется, т.е. полученная точность нас не устраивает (она больше, чем требуемая), то перейти к шагу 4; в противном случае прекратить вычисления, поскольку мы достигли требуемой точности, и приближенным корнем уравнения f (x) = 0 считать середину c отрезка .

Шаг 4. Определить интервал дальнейшего поиска корня. Из двух образовавшихся при делении отрезков переходим к той из его половин и , на концах которого функция принимает значения разных знаков.

Случай 1 (рис. 7). Корень на отрезке . , граница b сдвигается влево – заменить b на с : b := c .

С
лучай 2 (рис. 7). Корень на отрезке . , граница a сдвигается вправо – заменить a на с : a := c .

Рис. 7. Графическая иллюстрация метода половинного деления.

Перейти к шагу 1.

Алгоритм деления отрезка пополам довольно медленный, но зато абсолютно застрахован от неудач. Основное достоинство метода состоит в том, что его скорость сходимости не зависит от вида функции f (x). Данный метод не имеет дополнительных условий сходимости, кроме .

Так же есть методы хорд и касательных.

Графическое решение таких уравнений можно осуществить путем построения компьютерных моделей:

• построением графика функции в системе объектно-ориентированного программирования Visual Basic или Turbo Delphi

• в электронных таблицах Microsoft Excel или OpenOffice . org Calc путем построения диаграммы типа График

Найдем корень уравнения х3- cosx =0 приближенными методами (графическим и численным методом деления пополам числового отрезка аргумента)

Формальная модель задана уравнением, для нахождения корня уравнения разработаем компьютерную модель на языке Visual Basic .

1 Dim Graph1 As Graphics

Dim Pen1 As New Pen (Color.Black, 2)

Dim drawBrush As New SolidBrush (Color.Black)

Dim drawFont As New Font (“Arial”, 10)

Dim X , Y As Single

‘ Графическое решение уравнения

Private Sub Button1_Click(…)

Graph 1. Clear ( Color . White )

‘ Печать шкал математической системы координат в компьютерной системе координат

For X=-150 To 150 Step 50

Graph1.DrawString (X/100, drawFont,_

drawBrush, X+150, 50)

For Y=0 To 200 Step 50

Graph1.DrawString ((Y-150)/100, drawFont,_

drawBrush, 150, 200-Y)

‘ Преобразование компьютерной системы координат в математическую систему координат

Graph1.ScaleTransform(1, -1) ‘ поворот оси Y

Graph1.TranslaterTransform (150, -50) ‘ Сдвиг по осям X и Y

‘ Рисование осей математической системы координат

Graph1.DrawLine (Pen1, -150, 0, 300, 0) ‘ ось Х

Graph1.DrawLine (Pen1, 0, -150, 0, 50) ‘ ось Y

For X=-150 To 150 Step 50 ‘ засечки на оси Y

Graph1.DrawLine (Pen1, X, -5, X, 5)

For Y=-100 To 100 Step 50 ‘ засечки на оси Y

Graph1.DrawLine (Pen1, -5, Y, 5, Y)

For X=-1.5 To 1.5 Step 0.01

Graph1.DrawEllipse (Pen1, X*100, Y*100, 1, 1)

График функции пересекает ось Х один раз, следовательно, уравнение имеет один корень. По графику грубо приближенно можно определить, что х≈0.8 c м

Метод половинного деления

УТОЧНЕНИЕ КОРНЯ УРАВНЕНИЯ МЕТОДОМ ПОЛОВИННОГО ДЕЛЕНИЯ

При решении уравнения, как правило, заранее задается допустимая погрешность е приближенного значения корня E . В процессе уточнения корней требуется найти их приближенные значения, отличающиеся от точных не более чем на е .

Описанный выше способ табулирования может рассматриваться и как способ уточнения корня (хотя и крайне неэффективный). При этом можно либо постепенно уменьшать шаг табулирования, приближая его к значению е , либо сделать это сразу, полагая h = е . В любом случае получим b — а е . Тогда в качестве искомого значения корня можно выбрать середину этого отрезка, т.е. положить E = ( а + b )/2.

Гораздо более эффективным является так называемый метод половинного деления .

Пусть уравнение F(x)=0 имеет на отрезке [а; b] единственный корень, причем функция F ( x ) на этом отрезке непрерывна. Разделим отрезок [а; b] пополам точкой с = (а + b)/ 2. Если F ( c ) <> 0 (что практически наиболее вероятно), то возможны два случая: F ( x ) Меняет знак либо на отрезке [а; с] (рис. 2.6, а), либо на отрезке [a; b] (рис. 2.6, б). Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

Рис. 2.6. К решению уравнения F ( x ) методом половинного деления:

а — функция F ( x ) меняет знак на отрезке [а; с];

б — функция F ( x ) меняет знак на отрезке [c; b]

Метод половинного деления вполне можно использовать как метод решения уравнения с заданной точностью. Действительно, если на каком-то этапе процесса получен отрезок [а; b], содержащий корень, то, приняв приближенно х = (а + b)/2 , получим ошибку, не превышающую значения

(заметим, что речь в данном случае идет о погрешности метода). Метод половинного деления требует утомительных ручных вычислений, однако он легко реализуется с помощью программы на компьютере (блок-схему алгоритма см. на рис. 2.7). Отметим, что даже если на каком-то этапе деления отрезка пополам получится F ( c ) = 0, это не приведет к сбою алгоритма.

Рис. 2.7. Блок-схема алгоритма уточнения корня уравнения F ( x ) =0 на отрезке [ а; b ] с точностью е методом половинного деления

Использование метода половинного деления в написании программы.

Написание программы и составление интерфейса

Поместить на форму:

текстовые поля TextBox 1 и TextBox 2 для ввода числовых значений концов отрезка А и В;

текстовое поле TextBox 3 для ввода точности вычислений Р;

надпись Label 1 для вывода значений корня;

четыре надписи для вывода обозначений;

кнопку Button 2 для запуска обработчика событий

Ввести программный код, позволяющий вычислить корень уравнения методом половинного деления с использованием цикла с постусловием, который будет выполняться, пока выполняется условие (В-А)/2>P:

‘ численное решение уравнения

Dim A , B , C , P As Single

Private Sub Button2_Click(…)

If (A^3-Math.Cos(A) ) * (C^3-Math.Cos(C) )

Loop White (B-A)/2>P

Из графика функции видно, что корень находится на отрезке [0,5;1].Введем в текстовые поля значения концов числового отрезка, а также точность вычислений (например, 0,0001).

На надпись будет выведено значение корня: x ≈ 0,8654175

Точность вычисления корня зависит не только от параметров используемого численного метода, но и от типа переменной. В нашем случае имеет смысл говорить о математической точности результата, которая не может превышать точность числового метода, т.е. х≈0,8654.

Приближенное решение уравнений в электронных таблицах

Тип урока: Изучение и закрепление новых знаний.

Вид занятия: практическая работа с использованием компьютера.

Продолжительность занятия: два урока.

Цель: Научиться решать уравнения с заданной точностью на заданном отрезке.

развитие исследовательской, познавательной деятельности учащихся;
развитие умений использовать различные программные средства при решении одной задачи;
развитие коммуникативных способностей учащихся.

Методы обучения: наглядный, исследовательский, практический.

Операционная система Windows;
Microsoft Excel из пакета Microsoft Office;
Microsoft Visual Basic 6.0.

Организационный момент.
Создание проблемной ситуации.
Использование графического метода для приближенного решения уравнений в электронных таблицах.
Изучение метода половинного деления при решении уравнений.
Моделирование листа электронных таблиц для приближенного решения уравнения методом половинного деления.
Моделирование проекта “Приближенное решение уравнения” на объектно-ориентированном языке Visual Basic 6.0.
Компьютерный эксперимент.
Анализ полученных результатов.
Подведение итогов урока.

1. Организационный момент.

2. Создание проблемной ситуации.

3. Использование графического метода для приближенного решения уравнений в электронных таблицах.

– Что нужно определить для построения графика? (Отрезок, на котором существует корень.)

4. Изучение метода половинного деления при решении уравнений.

Практическая работа

Приближенное решение уравнений

Просмотр содержимого документа
«Практическая работа Приближенное решение уравнений»

Приближенное решение уравнений

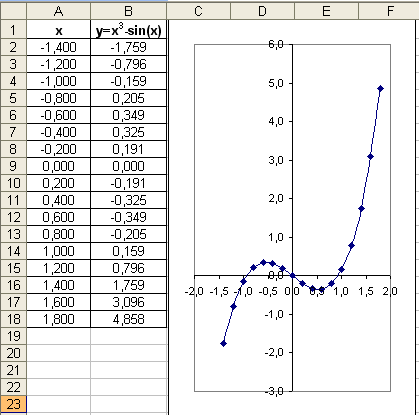
Создать компьютерную модель «Приближенное решение уравнений» с использованием электронных таблиц Microsoft Excel, которая позволяет найти корень уравнения x 3 = sin x приближенными методами (графическим и с помощью метода Подбор параметра).

Представить функцию в табличной форме, построить ее график, который позволит определить корни уравнения грубо приблизительно.

Представить заданное уравнение в табличной форме.

Для грубо приближенного определения корня построить диаграмму типа график. По графику грубо приближенно можно определить, что х=0,8.

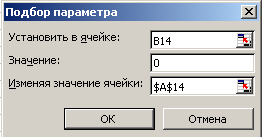
Для поиска решения с заданной точностью используем метод Подбор параметра. Точность подбора зависит от заданной точности представления чисел в ячейках таблицы (например, до трех знаков после запятой). Методом подбора параметра необходимо определить значение аргумента х (ячейка В14) равно нулю.

Выделить ячейку со значением функции В14 и ввести команду [Сервис-Подбор параметра…].

На панели Подбор параметра в поле Значение ввести требуемое значение функции (в данном случае 0).

В поле Изменяя значение ячейки ввести адрес ячейки $А$14, в которой будет производиться подбор значения аргумента, и щелкнуть по кнопке ОК.

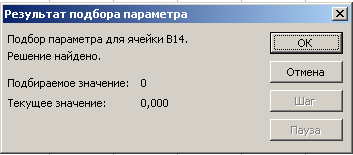
На панели Результат подбора параметра будет выведена информация а величине подбираемого и подобранного значений.

В ячейке аргумента А14 появится подобранное значение 0,929. Таким образом, корень уравнения х=0,929 найден с заданной точностью.

Аналогично определите второй корень уравнения.

Задание для самостоятельной работы. Создать компьютерную модель «Приближенное решение уравнений» с использованием электронных таблиц Microsoft Excel, которая позволяет найти корень уравнения х 3 = sin х графическим способом.

Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .

Описание презентации по отдельным слайдам:

Приближенное решение уравнений c помощью электронных таблиц MS EXСEL

1 способ графического решения уравнений с одним неизвестным Пусть дано уравнение f(x)=g(x). Приведем это уравнение к виду f(x)-g(x)=0 Введем функцию у=f(x)-g(x). Построим график этой функции Количество точек пересечения графика с осью абсцисс дает число корней уравнения Абсциссы точек пересечения и есть решения данного уравнения

2 способ графического решения уравнений с одним неизвестным Пусть дано уравнение f(x)=g(x). Введем функции у= f(x) и у =g(x). Построим графики этих функций в одной системе координат. Количество точек пересечения дает число корней уравнения. Абсциссы точек пересечения и есть решения данного уравнения.

Алгоритм использования команды Подбор параметра: Решить нужную задачу с каким – либо начальным значение параметра; Выбрать команду Подбор параметра в меню Сервис; В появившемся окне диалога Подбор параметра в поле Установить в ячейке указывается адрес ячейки, значение в которой нужно изменить (такая ячейка называется целевой); В поле Значение – то числовое значение, которое должно появиться в целевой ячейке; В поле Изменяя значение ячейки ввести ссылку на ячейку с параметром

Использование надстройки Подбор параметра для 1 способа По графику видно, что ближайший аргумент к точке пересечения оси Х с графиком функции равен -1,1. По таблице значений функции можно определить, что этот аргумент функции хранится в ячейке А5 Выделить ячейку В5 со значением функции и выполним команду Сервис-Подбор параметра…. В диалоговом окне в поле Значение: ввести требуемое значение функции (0). В поле Изменяя значение ячейки: ввести адрес $A$5, в который будет производится подбор значения аргумента. Кнопка ОК В ячейке аргумента A5 появится подобранное значение – 1,296. Корень уравнения найден с заданной точностью.

Графическое решение систем уравнений с двумя неизвестными Пусть дана система уравнений f(x,y)=0 и y(x,y)=0 1. Рассмотрим каждое из них в виде y=f(x) и y=u(x); 2. Построим эти кривые на одном графике; 3. Определим координаты точек их пересечения, что будет являться решением исходной системы уравнений.

х1≈-0,5 у1≈5 х2≈1,5 у2≈5

Домашнее задание: 1. § 1.3.4 Н.Д.Угринович «Информатика и ИКТ» 11 класс – вопросы 1,2 2. Практическое задание: решить графически систему уравнений

1 способ графического решения уравнений с одним неизвестным

Пусть дано уравнение

Приведем это уравнение к виду f(x) — g(x) =0 Введем функцию у= f ( x )- g ( x ). Построим график этой функции Количество точек пересечения графика с осью абсцисс дает число корней уравнения

Абсциссы точек пересечения и есть решения данного уравнения 2 способ графического решения уравнений с одним неизвестным

Пусть дано уравнение f(x)=g(x) .

Введем функции у= f ( x ) и у = g ( x ). Построим графики этих функций в одной системе координат. Количество точек пересечения дает число корней уравнения. Абсциссы точек пересечения и есть решения данного уравнения.

Барсуков Сергей ВладимировичНаписать 1577 16.01.2015

Номер материала: 306027

16.01.2015 2520

16.01.2015 1574

16.01.2015 784

16.01.2015 489

16.01.2015 383

16.01.2015 572

16.01.2015 647

Не нашли то что искали?

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

источники:

http://infourok.ru/priblizhennoe-reshenie-uravneniy-na-yazike-visual-basic-1998233.html

http://planshet-info.ru/kompjutery/priblizhennoe-reshenie-uravnenij-v-jelektronnyh