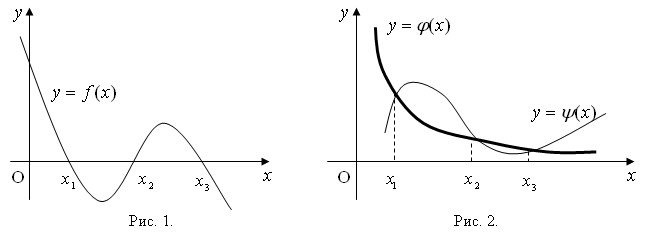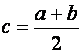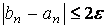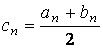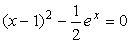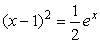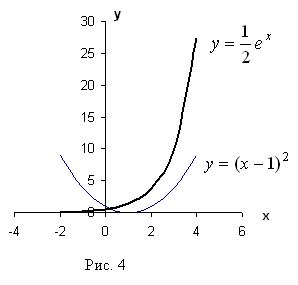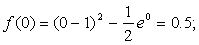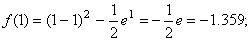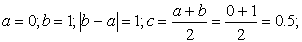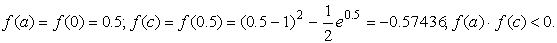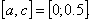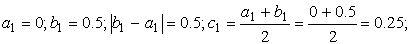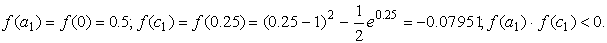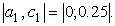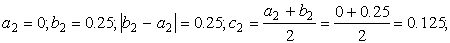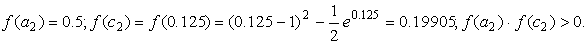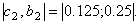Приближенное решение уравнений отделение корней

Приближенное решение уравнений отделение корней

1. Приближенное решение нелинейных уравнений

Пусть дано уравнение с одним неизвестным

, (1.1)

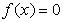
где f ( x ) — заданная алгебраическая или трансцендентная функция.

Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций — показательная , логарифмическая, тригонометрические, обратные тригонометрические.

Решить уравнение — значит найти все его корни, то есть те значения х , которые обращают уравнение в тождество, или доказать, что корней нет.

В общем случае не существует формул, по которым определяются точные значения корней уравнения (1.1). Для отыскания корней используют приближенные методы, при этом корни находятся с некоторой заданной точностью ε . Это означает, что если x — точное значение корня уравнения, а x ’ — его приближенное значение с точностью ε , то | x — x ’ | ≤ ε . Если корень найден с точностью ε , то принято писать x = x ± ε .

Будем предполагать, что уравнение (1.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.

Приближенное решение уравнения состоит из двух этапов:

1. Отделение корней, то есть нахождение интервалов из области определения функции f ( x ), в каждом из которых содержится только один корень уравнения (1).

2. Уточнение корней до заданной точности.

Отделение корней можно проводить графически и аналитически.

Для того , чтобы графически отделить корни уравнения (1.1), строят график функции y = f ( x ). Абсциссы точек его пересечения с осью Ox есть действительные корни уравнения (рис. 1). Практически бывает удобнее заменить уравнение (1.1) равносильным ему уравнением

, (1.2)

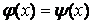
где Φ( x ) и Ψ( x ) — более простые функции, чем f ( x ). Абсциссы точек пересечения графиков функций y = Φ( x ) и y = Ψ( x ) дают корни уравнения (1.2), а значит и исходного уравнения (1.1) (рис.2).

Аналитическое отделение корней основано на следующей теореме: если непрерывная на отрезке [ a , b ] функция y = f ( x ) принимает на концах отрезка значения разных знаков, т.е. f ( a )· f ( b ) f ( x ) = 0; если при этом производная f ’ ( x ) сохраняет знак внутри отрезка [ a , b ], то корень является единственным.

Уточнение корней заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Рассмотрим самый простой из них — метод половинного деления.

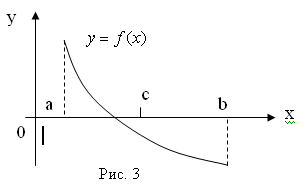
Пусть корень отделён и принадлежит отрезку [ a , b ]. Находим середину отрезка [ a , b ] по формуле

Если f ( c ) = 0, то с — искомый корень. Если f ( c ) ≠ 0, то в качестве нового отрезка изоляции корня [ a ₁ , b ₁ ] выбираем ту половину [ a , c ] или [ c , b ], на концах которой f ( x ) принимает значения разных знаков. Другими словами, если f ( a ) ∙ f ( c ) a , c ], если f ( a ) ∙ f ( c ) — отрезку [ c , b ]. Полученный отрезок снова делим пополам, находим c₁ ,

вычисляем f ( c ₁ ), выбираем отрезок [ a ₂ , b ₂ ] и т.д. Длина каждого нового отрезка вдвое меньше длины предыдущего, то есть за n шагов отрезок сократится в 2 n раз. Как только будет выполнено условие

то в качестве приближенного значения корня, вычисленного с точностью ε , можно взять

Пример . Пусть требуется решить уравнение

с точностью ε = 0,0001. Отделим корень графически. Для этого преобразуем уравнение к виду

и построим графики функций (рис. 4):

Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку [0; 1].

Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка [0; 1] имеем:

. Следовательно, корень отделён правильно.

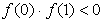
Уточнение корня выполним методом половинного деления.

Корень принадлежит отрезку

Корень принадлежит отрезку

Корень принадлежит отрезку

Лекция «Приближенные решения алгебраических и трансцендентных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

БИК Курс лекций по дисциплине «Численные методы»

для специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем

Раздел 2. Численные методы

2.1.1. Приближенные решения алгебраических и трансцендентных уравнений

Алгебраические и трансцендентные уравнения

Графический метод решения уравнений

1. Алгебраические и трансцендентные уравнения

При решении практических задач часто приходится сталкиваться с решением уравнений. Всякое уравнение с одним неизвестным можно представить в виде

( x )= g ( x ), (1)

где (х) и g (х) — данные функции, определенные на некотором числовом множестве X , называемом областью допустимых значений уравнения .

В общем случае нелинейное уравнение можно записать в виде:

F ( x ) определена и непрерывна на конечном или бесконечном интервале .

 Совокупность значений переменной х, при которых уравнение (1) превращается в тождество, называется решением этого уравнения, а каждое значение х : из этой совокупности называется корнем уравнения.

 Всякое число , обращающее функцию F ( x ) в нуль, т.е. такое, при котором F ( )=0, называется корнем уравнения (1).

 Число называется корнем k -той кратности, если при x =вместе с функцией F ( x ) равны нулю ее производные до ( k -1) порядка включительно:

F ( ) = F / () = … = F ( k -1) ( ) = 0.

Однократный корень называется простым.

 Решить уравнение – значит найти множество всех корней этого уравнения.

Оно может быть конечным или бесконечным.

 Два уравнения F ( x )=0 и G ( x =0) называются равносильными (эквивалентными), если всякое решение каждого из них является решением и для другого, то есть множества решений этих уравнений совпадают.

В зависимости от того, какие функции входят в уравнения (1) или (2), уравнения разделяются на два больших класса: линейные и нелинейные.

Нелинейные уравнения делятся, в свою очередь на: алгебраические и трансцендентные .

Уравнение (2) называется алгебраическим, если функция является алгебраической функцией. Путем алгебраических преобразований из всякого алгебраического уравнения можно получить уравнение в канонической форме:

где a ₀, a ₁, . , a _n — коэффициенты уравнения, а x -неизвестное. Показатель n называется степенью алгебраического уравнения.

Если функция F ( x ) не является алгебраической, то уравнение (1) называется трансцендентным.

В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений.

Решение уравнения с одним неизвестным заключается в отыскании корней, т. е. тех значений х, которые обращают уравнение в тождество. Корни уравнения могут быть вещественными и невещественными (комплексными).

Найти точные значения корней уравнения можно только в исключительных случаях, обычно, когда есть какая-либо простая формула для вычисления значения корней, выражающая их через известные величины.

Поскольку подавляющее большинство нелинейных уравнений с одной переменой не решаются путем аналитических преобразований (точными методами), на практике их решают только численными методами.

При решении многих практических задач точное решение уравнения не всегда является необходимым. Задача нахождения корней считается решенной, если корни вычислены с заданной степенью точности.

 Решить уравнение – это значит

установить, имеет ли оно корни,

и найти значение корней с заданной точностью.

 Задача численного нахождения действительных и комплексных корней уравнения (2) обычно состоит из двух этапов:

отделение корней, т.е. нахождение достаточно малых окрестностей рассматриваемой области, в которых находится одно значение корня,

и уточнение корней, т.е. вычисление корней с заданной степенью точности в некоторой окрестности.

Наиболее распространенными на практике численными методами решения уравнения (2) являются: метод половинного деления, метод хорд, метод касательных (Ньютона), комбинированный метод, метод простой итерации. Применение того или иного метода для решения уравнения (2) зависит от числа корней, задания исходного приближения и поведения функции F ( x ).

2. Графические методы решения уравнений

Одним из методов решения уравнений является графический. Точность такого решения невелика, однако с помощью графика можно разумно выбрать первое приближение, с которого начнется дальнейшее решение уравнения. Существуют два способа графического решения уравнений.

Первый способ. Все члены уравнения переносят в левую часть, т. е. представляют его в виде f (х) = 0. После этого строят график функции у = f ( x ), где f (х) – левая часть уравнения. Абсциссы точек пересечения графика функции у = f (х) с осью Ох и являются корнями уравнения, так как в этих точках у = 0 (рис. 1).

Рисунок 1

Второй способ. Все члены уравнения разбивают на две группы, одну из них записывают в левой части уравнения, а другую в правой, т. е. представляют его в виде f (х) = g (х).

После этого строят графики двух функций у = f (х) и у = g (х). Абсциссы точек пересечения графиков этих двух функций и служат корнями данного уравнения. Пусть точка пересечения графиков имеет абсциссу х₀, ординаты обоих графиков в этой точке равны между собой, т. е. f (х₀) = g (х₀). Из этого равенства следует, что х₀ – корень уравнения (рис. 2).

Рисунок 2

Пример 1. Решить графически уравнение х 3 — 2 x 2 + 2х — 1 = 0.

Первый способ. Построим график функции у = х 3 — 2 x 2 + 2х — 1 и определим абсциссы точек пересечения этого графика с осью Ох. Кривая пересекает ось Ох в точке х = 1, следовательно, уравнение имеет один корень (рис. 3). (Отметим, что алгебраическое уравнение третьей степени имеет или один действительный корень или три. Так как кривая пересекает ось абсцисс только в одной точке, то данное уравнение имеет только один действительный корень. Остальные два корня – комплексные.)

Рисунок 3 Рисунок 4

Второй способ. Представим данное уравнение в виде х 3 = 2 x 2 + 2х–1 и построим графики функций у = х 3 и у = 2 x 2 + 2х – 1. Найдем абсциссу точки пересечения этих графиков; получим х = 1 (рис. 4).

Пример 2. Найти приближенно графическим способом корни уравнения lg х — Зх + 5 = 0.

Перепишем уравнение следующим образом: lg х = Зх — 5.

Функции в левой и в правой части уравнения имеют общую область определения: интервал 0

Строим графики функций у = lg х и у = Зх — 5 (рис. 5). Прямая у = Зх-5 пересекает логарифмическую кривую в двух точках с абсциссами x ₁ 0,00001 и x ₂ 1,75. На рисунке трудно показать пересечение графиков этих двух функций в первой точке, однако, учитывая, что нижняя ветвь, логарифмической кривой неограниченно приближается к оси Оу, можно предполагать, что пересечение этих двух графиков произойдет вблизи точки пересечения графика функции у = Зх — 5 и оси Оу. Абсцисса точки пересечения приближенно равна 0,00001. Итак, корни уравнения x ₁ 0,00001 и x ₂ 1,75

Рисунок 5 Рисунок 6

Пример 3. Найти графически корни уравнения 2 х = 2х.

Решение. Строим графики функций у = 2 х и у = 2х. Эти графики пересекаются в двух точках, абсциссы которых равны х ₁ = 1 и х ₂ = 2. Данное урав­нение имеет два корня х ₁ = 1 и х ₂ = 2 (рис. 6).

Подводя итог вышеизложенному, можно рекомендовать для графического решения уравнения f (х) = 0, все корни которого лежат в промежутке [а, b ], следующую простую схему.

1. Представить указанное уравнение в виде (х) = g (х) с таким расчетом, чтобы функции у=(х) и у = g (х) были просты и удобны для исследования и построения.

2. На бумаге вычертить графики функций у =(х) и у = g (х) в промежутке [а, b ].

3. Если графики не пересекаются, то корней в данном промежутке нет. Если же графики пересекаются, то нужно определить точки их пересечения, найти абсциссы этих точек, которые и будут приближенными значениями корней рассматриваемого уравнения.

Первый этап численного решения уравнения (2) состоит в отделении корней, т.е. в установлении “тесных” промежутков, содержащих только один корень.

 Корень уравнения f (х) = 0 считается отделенным на отрезке [ a , b ] , если на этом отрезке уравнение f (х) = 0 не имеет других корней.

 Отделить корни – это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень.

Отделение корней можно произвести двумя способами – графическим и аналитическим.

Графический метод отделения корней. При графическом методе отделения корней поступают так же, как и при графическом методе решения уравнений.

Графический метод отделения корней не обладает большой точностью. Он дает возможность грубо определить интервалы изоляции к орня. Далее корни уточняются одним из способов, указанных ниже.

Аналитический метод отделения корней. Аналитически корни уравнения f(х) =0 можно отделить, используя некоторые свойства функций, изучаемые в курсе математического анализа.

Сформулируем без доказательства теоремы, знание которых необходимо при отделении корней.

1) Если непрерывная на отрезке функция F ( x ) принимает на его концах значения разных знаков, то уравнение (2) имеет на этом отрезке, по меньшей мере, один корень

2) Если функция F ( x ) к тому же еще и строго монотонна, то корень на отрезке единственный.

Рассмотрим примеры поведения некоторых функций:

Рисунок 7

Для отделения корней можно эффективно использовать ЭВМ.

Пусть имеется уравнение F ( x )=0, причем можно считать, что все корни находятся на отрезке , в которой функция F ( x ) отделена, непрерывна и F ( A )* F ( B ) F ( x ), начиная с точки X = A , двигаясь вправо с некоторым шагом h .

Как только обнаружится пара соседних значений F ( x ), имеющих разные знаки, и функция F ( x ) монотонна на этом отрезке, так соответствующие значения аргумента X (предыдущее и последующее) можно считать концами отрезка, содержащего корень.

Схема соответствующего алгоритма изображена ниже. Результатом решения поставленной задачи будут выводимые на дисплей в цикле значения параметров X ₁ и X ₂ (Концов выделенных отрезков).

Модуль 1. Модуль 1. Численные методы решения нелинейных уравнений. Нахождение арифметического корня натуральной степени с заданной точностью

Модуль 1. Модуль 1. Численные методы решения нелинейных уравнений. Нахождение арифметического корня натуральной степени с заданной точностью.

1. Численные методы решения нелинейных уравнений.

1.1. Постановка задачи.

1.2. Этапы приближенного решения нелинейных уравнений.

1.3. Уточнение корней методом деления отрезка пополам.

1.4. Уточнение корней методом касательных.

1.5. Уточнение корней методом хорд.

2. Нахождение арифметического корня натуральной степени с заданной точностью.

Литература.

1. Численные методы решения нелинейных уравнений.

1.1. Постановка задачи.

Пусть имеется уравнение вида

где f (x) — заданная алгебраическая или трансцендентная функция. (Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций — показательная, логарифмическая, тригонометрические, обратные тригонометрические.)

Решить уравнение — значит найти все его корни, то есть те значения x, которые обращают уравнение в тождество, или доказать, что корней нет.

Если алгебраическое или трансцендентное уравнение достаточно сложно, то довольно редко удается точно найти его корни. Кроме того, в некоторых случаях уравнение может содержать коэффициенты, известные лишь приблизительно, поэтому сама задача о точном нахождении корней теряет смысл. В таких случаях применяют численные (приближенные) методы решения.

Поставим задачу найти такое приближенное значение корня xпр, которое мало отличается от точного значения корня x*, так что выполняется неравенство │x* – xпр │ 0, m – натуральное.

Известен следующий рекуррентный (итерационный) процесс нахождения членов последовательности t0, t1, t2, …, где

, n = 0, 1, 2, … . (6)

При этом оказывается [4], что полученная последовательность сходится при любом t0>0 к точному значению и при том достаточно быстро.

Удобно в качестве t0 брать значение с одной верной значащей цифрой, которую легко найти подбором.

Итерационный процесс нахождения очередного приближения к величине корня прекращается, как только выполнится неравенство . При этом с точностью ε.

Пример 5. Найти с точностью ε = 0,000001 (или ε = 10-6).

Решение. Здесь a = 1,25, ε = 10-6. Пусть t0 = 1,1 (т. к. 1,12≈1,25). Из формулы (6) при m = 2 имеем:

, n = 0, 1, 2, … .

Значит . Так как требуется найти значение корня с точностью ε = 10-6, т. е. с шестью верными значащими цифрами после запятой, при вычислении t1 количество цифр после запятой берем с запасом (например, семь цифр).

Аналогично вычисляем t2 = 1,1180339…; . Продолжаем итерационный процесс: t3 = 1,1180339… . Итак, на третьем шаге (итерации) результат в требуемых знаках (шесть цифр после запятой) повторился, т. е. .

Значит, с точностью 10-6.

3. Практикум.

Численные методы решения нелинейных уравнений.

В заданиях данной группы нужно выбрать правильные ответы из приведенного списка. Обратите внимание, что правильный ответ может быть не единственным. Вам надо указать через запятую буквы соответствующие правильным высказываниям.

1. Какие из следующих функций являются трансцендентными?

2. Поиск корней методом половинного деления применим к функциям:

a) к многочленам любых степеней.

b) к непрерывным, но не дифференцируемым функциям.

c) к функциям, имеющим разрывы.

d) любым непрерывным.

3. Отметьте высказывания, относящиеся к поиску корней методом половинного деления:

a) Существуют уравнения, для которых есть только численное решение и нет аналитического.

b) Это самый быстрый метод поиска корней.

c) Это самый точный метод.

d) Это один из самых простых вычислительных методов поиска корней уравнения

e) Этот метод не требует дополнительных условий сходимости.

f) Этим методом можно искать корни многочленов любых степеней.

В заданиях данной группы нужно выбрать правильный ответ из приведенного списка. Обратите внимание, что правильный ответ должен быть единственным

4. Решить уравнение, значит

a) найти такие значения неизвестного, которые при подстановке в уравнение, обращают его в тождество;

b) доказать, что таких значений неизвестного, которые при подстановке в уравнение, обращают его в тождество нет;

c) найти такие значения неизвестного, которые при подстановке в уравнение, обращают его в тождество или доказать, что корней нет;

d) найти такие значения неизвестного, которые при подстановке в уравнение, обращают его в верное тождество и доказать, что корней нет.

5. Для какой из приведенных ниже функций y = f(x) уравнение f(x) = 0 не имеет корней

6. Отделение корней уравнения f(x)=0 – это

a) нахождение интервалов длиной ε из области определения функции y=f(x);

b) нахождение корней из области определения функции y=f(x);

c) нахождение интервалов с одним корнем вне области определения функции y=f(x);

d) нахождение интервалов из области определения, в каждом из которых содержится ровно один корень.

7. Какая из этих формул верна и применяется в методе деления отрезка пополам для определения достижения точности?

8. Какая из этих формул верна и применяется в методе деления отрезка пополам для определения X – приближённого значение корня на отрезке [a; b]?

9. Аналитическое отделение корней уравнения f(x) = 0 основано на теореме:

a) если функция f(x) непрерывна на [a, b], принимает на концах отрезка значения разных знаков, то на этом отрезке содержится хотя бы один корень;

b) если f ‘(x) существует и непрерывна, то на этом отрезке содержится хотя бы один корень;

c) если функция f(x) принимает на концах отрезка [a, b] значения разных знаков, то на этом отрезке содержится хотя бы один корень;

d) если f ‘(x) непрерывна и меняет знак на [а, b], то на этом отрезке содержится хотя бы один корень.

10. Необходимым условием сходимости метода касательных при решении уравнения у = f(x) является:

a) f(x) непрерывна на [a, b] и сохраняет на нем свой знак;

b) f ‘(x) существует и сохраняет знак;

c) f(x) и f ‘(x) непрерывны на [a, b] и сохраняют знак;

d) f(x) непрерывна и меняет знак на отрезке [a, b], f ‘(x) непрерывна и сохраняет знак на отрезке [a, b].

11. Укажите интервал изоляции корня уравнения .

12. Какому графику соответствуют условия , , , , ?

13. Известно, что уравнение имеет три корня. Минимальное количество начальных точек, определяющих отрезки изоляции корней, для полного решения методом половинного деления:

В заданиях данной группы нужно вписать числовой ответ или дополнить предложение.

14. Дано нелинейное уравнение x2sinx + 1 = 0 и начальное приближение x0 = 3,3. Первое приближение x1 в методе Ньютона равно (ответ округлить до трех знаков после запятой) ____________.

15. Дано уравнение x2sinx + 1 = 0. Известно, что на отрезке [3,2; 3,5] существует единственный корень уравнения. После выполнения одного шага методом деления отрезка пополам, отрезок станет равен _____________________________.