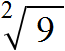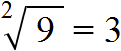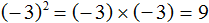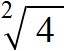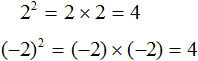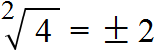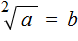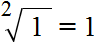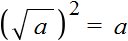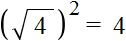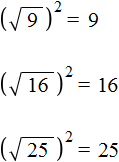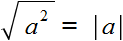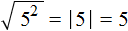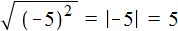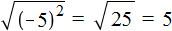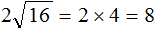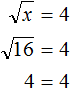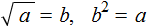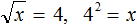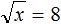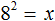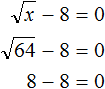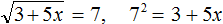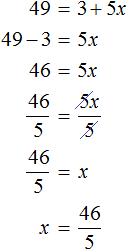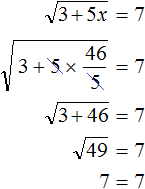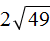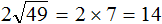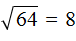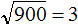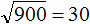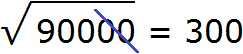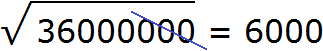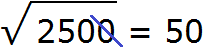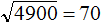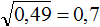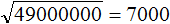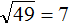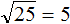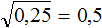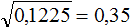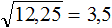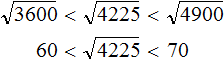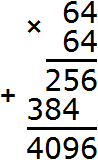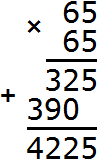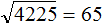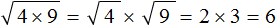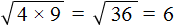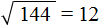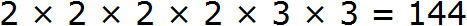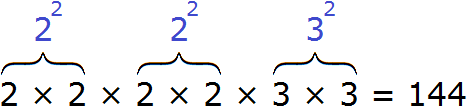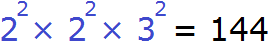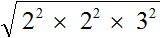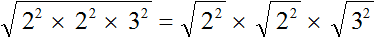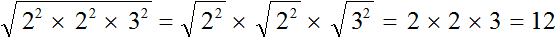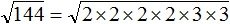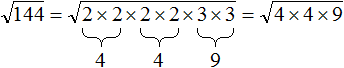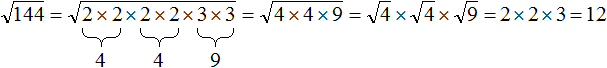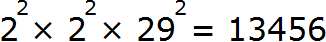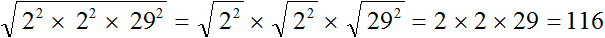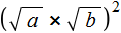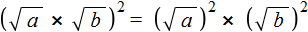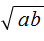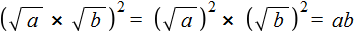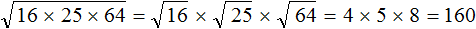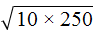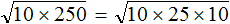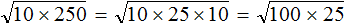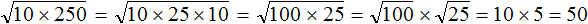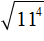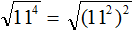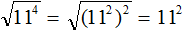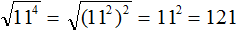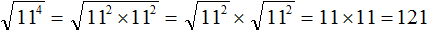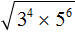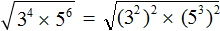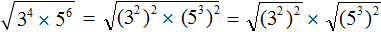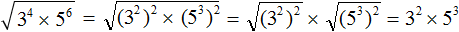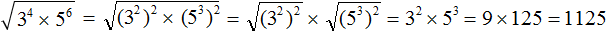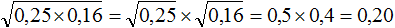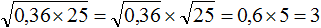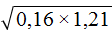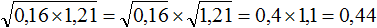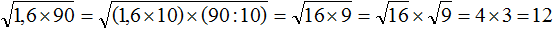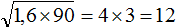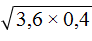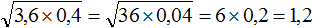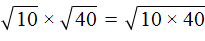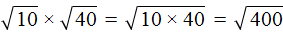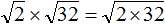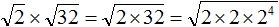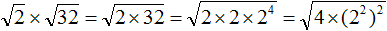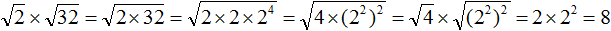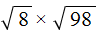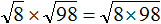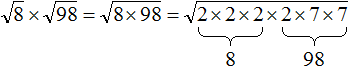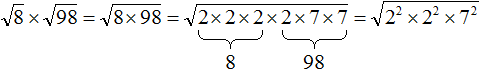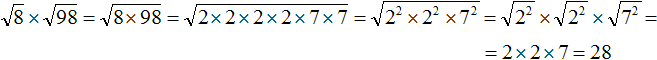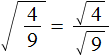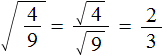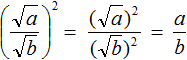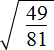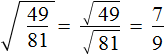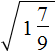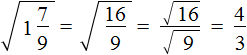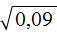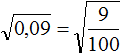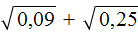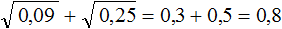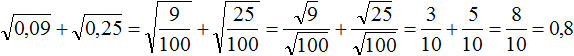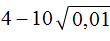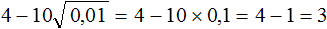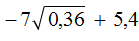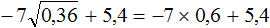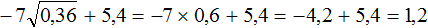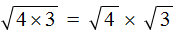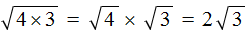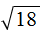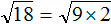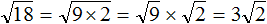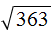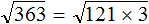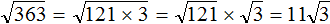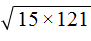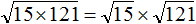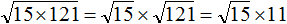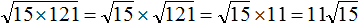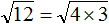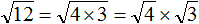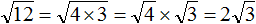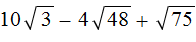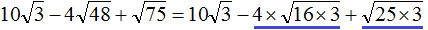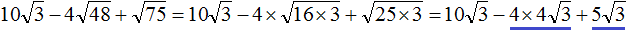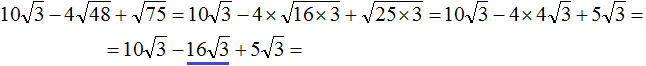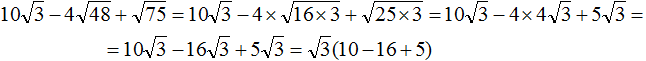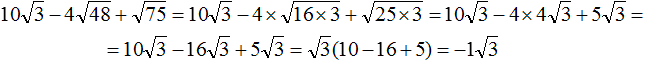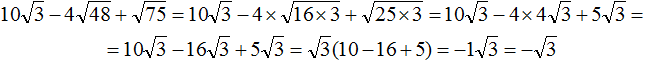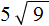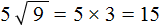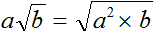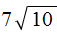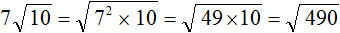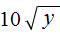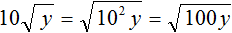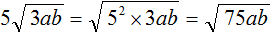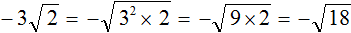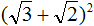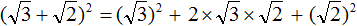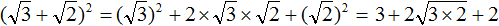Приближенное вычисление корней в уравнениях
Приближенное вычисление корней в уравнениях
- Приближённое решение уравнений :
1.1 Способ хорд (или способ линейной интерполяции).
- Способ касательных (или способ Ньютона).
- Комбинированный способ (комбинированное применение способов хорд и касательных).
Приближённое решение уравнений.
Если квадратные уравнения решали уже древние греки, то способы решения алгебраических уравнений третьей и четвёртой степени были открыты лишь в XVI веке. Эти классические способы дают точные значения корней и выражают их через коэффициенты уравнения при помощи радикалов различных степеней. Однако эти способы приводят к громоздким вычислениям и поэтому имеют малую практическую ценность.
В отношении алгебраических уравнений пятой и высших степеней доказано, что в общем случае их решения не выражаются через коэффициенты при помощи радикалов. Не выражаются в радикалах, например, корни уже такого простого по виду уравнения, как:
Сказанное, однако, не означает отсутствия в науке методов решения уравнения высших степеней. Имеется много способов приближенного решения уравнений — алгебраических и неалгебраических (или, как их называют, трансцендентных), позволяющих вычислять их корни с любой, заранее заданной степенью точности, что для практических целей вполне достаточно.
На простейших из таких способов мы и остановимся, причём речь будет идти о вычислении действительных корней.
Пусть нужно решить уравнение:
Если обратиться к рисунку, то каждый корень уравнения (1) представляет собой абсциссу точки пересечения графика функции y=f(х)
C осью Ох (рисунок №1)
С помощью графика функции или каким-нибудь иным способом обычно удаётся установить приблизительные значения корней. Это позволяет для каждого корня получить грубые приближения по недостатку и по избытку. Такого рода грубых приближений во многих случаях оказывается достаточно, чтобы, отправляясь от них, получить все значения корня с требуемой точностью. Об этом и пойдёт речь.
Итак, пусть корень Е уравнения (1) «зажат» между двумя его приближениями а и b по недостатку и по избытку а
Способ хорд (или способ линейной интерполяции).
Проведём хорду АВ (рисунок№3) и за первое приближённое значение корня примем абсциссу x1 точки С пересечения хорды с осью Ох.
Уравнение хорды имеет вид:
Поэтому в точке С:
Рассмотрение всех четырёх случаев, изображённых на рисунке №2, показывает, что точка x1 лежит между a и b с той стороны от Е, где f(х) имеет знак, противоположный знаку f«(х).
Остановим внимание на первом случае: f`(х)>0, f«(х)>0 (рисунок №3), — в остальных случаях рассуждение вполне аналогично. В этом первом случае x1 лежит между a и Е. С отрезком [x1, b] поступаем так же, как мы поступаем с отрезком [a, b] (рисунок №4). При этом для нового приближённого значения корня получаем:
x1 = x2-(b- x1)*f(x1)/f(b)-f(x1)
( в формуле (2) заменяем x1 на x2, а на x1 ); значение x2 оказывается между x1 и Е. Рассматриваем отрезок [x2, b] и находим новое приближённое x3, заключённое между x2 и Е и. т. д. В результате получим последовательность а 0
Найдём первое приближённое значение корня по формуле (2):
так как f(1,588)=-0,817 0
Следовательно, искомый корень с точностью до 0,01 равен 1,64.
1.2 Способ касательных (или способ Ньютона).
В том из концов дуги АВ (рисунок №5), в котором знаки f(х) и f«(х) совпадают, проводим касательную и за первое приближённое значение корня принимаем абсциссу х1` точки Д пересечения этой касательной с осью Ох. Обратимся вновь к первому случаю, соответствующему первому рисунку №2 (f`(x)>0, f«(x)>0), — в остальных случаях рассуждают опять-таки аналогично. Уравнение интересующей нас касательной имеет вид:
и поэтому в точке Д:
Из рисунка видно, что x1` лежит между Е и b. С отрезком [a, x1`] поступаем так же, как с отрезком [a, b] ( рисунок №5), и в результате для нового приближённого значения корня получим:
х2` = x1`- f( x1`)/ f`( x1`).
Значение х2` оказывается между Е и x1`. Рассматриваем отрезок [a, х2`] и находим новое приближение х3` и т. д. В результате получим последовательность:
все более точных приближённых значений корня, причём:
xn+1`= xn`- f(xn`)/ f`( xn`) (8)
Эта формула справедлива для всех четырёх случаев, изображённых на рисунке 32. Для оценки погрешностей полученных приближений можно опять воспользоваться формулой (5), как и в первом случае, легко устанавливается сходимость последовальности x1`, х2`, х3`,…,xn`,… к значению Е
Пример №2. Методом касательных найдём положительный корень уравнения
с точностью до 0,01.
В этом уравнении f(х)=х^4-2x-4, f`(х)=4х^3-2,а f«(х)=12x^2.Так как f(х) и f«(х) при х0 = 1,7 имеют один и тот же знак, а именно:
f(1,7)=0,952>0 и f«(1,7)>0, то применяем формулу:
x1`= х0- f(х0)/ f`( х0), где f`(1,7)=4*1,7^3-2=17,652. Тогда
Применяем второй раз способ касательных:
х2= x1- f(x1)/ f` (x1), где f(x1)= f(1,646)=0,048, f` (1,646) =15,838;
f(1,643)=0,004, f` (1,643)=15,740;
Следовательно, искомый корень с точностью до 0,01 равен 1,64.
1.3 Комбинированный способ
(комбинированное применение способов хорд и касательных).
Этот способ состоит в одновременном использовании способов хорд и касательных. Остановим своё внимание опять на случае, отвечающем первому рисунку №2. Значения x1 и x1`, вычисляем по прежним формулам, т. е. принимаем:
x1`=b-f(b)/f`(b), причём: x1 0 изображён на рисунке №7. Из этого рисунка видно, что уравнение имеет положительный единственный корень, лежащий на отрезке 1 0,f«(x)>0 т. е. знак производных сохраняется. Применяем комбинированный способ:
Формулы (10) дают:
При этом x1`- x1=0,012, т. е. точность недостаточна. Совершаем второй шаг:
При этом х2`- х2=0,00018, т. е. точность достаточна. Таким образом:
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
Приближенные методы извлечения квадратного корня (без использования калькулятора).
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Извлечение квадратного корня «вручную»
На примере возьмём число 223729. Для извлечения корня мы должны проделать следующие операции:
А) разбить число справа на лево на разряды по две цифры в разряде, ставя штрихи наверху- 223729→ 22’37’29’. Если бы это было число с нечётным числом цифр, как например, 4765983, то при разбиении к первой цифре слева надо приписать нуль, т.е. 4765983→04’76’59’83’.
Б) Навесить на число радикал и написать знак равенства:
22’37’29’→
После этого начинаем, собственно, вычислять корень. Это делается шагами, причём на каждом шаге обрабатывается один разряд исходного числа, т.е. две очередных цифры слева направо, и получается одна цифра результата.
Шаг 1 ― извлечение квадратного корня с недостатком из первого разряда:

Итог шага 1 есть первая цифра искомого числа:

Шаг 2 ― первую полученную цифру возводим в квадрат, приписываем под первым разрядом и ставим знак минус вот так:



И производим вычисление так, как это уже написано.
Шаг 3 ― приписываем справа к результату вычитания две цифры следующего разряда и слева от получившегося числа ставим вертикальную черту вот так:




После этого, воспринимая цифры, стоящие после знака =, как обычное число, умножаем его на 2 и приписываем слева от вертикальной черты пропуск, в котором ставим точку и под этой точкой тоже ставим точку:


Поставленная точка обозначает поиск цифры. Эта цифра будет второй в итоговом числе, т.е. встанет после цифры 4. Ищется она по следующему правилу:
Это наибольшая цифра k такая, что число 8 k , т.е. число, получающееся из 8 приписыванием цифры k , умноженное на k , не превосходит 637.
В данном случае это цифра 7, т.к. 87∙7=609 637. Итак, мы имеем:

Шаг 4 ― проведём горизонтальную черту и под ней запишем результат вычитания:
637 – 609 = 28. К числу 28 приписываем последний разряд исходного подкоренного числа и получим число 2829. Слева от него проводим вертикальную черту, умножаем теперь уже 47 на 2 и полученное число 94 приписываем слева от вертикальной черты, оставив место в виде точки для поиска последней цифры. Цифра 3 подходит в точности без остатка, так как 943∙3=2829, значит, это последняя цифра искомого числа, т.е. 


В принципе, если бы остаток получился ненулевой, можно было бы поставить после найденных цифр числа запятую, списать в качестве следующего разряда два десятичных знака числа, или два нуля, если таковые отсутствуют, и продолжать все более и более точно извлекать квадратный корень. Вот например:


Приближенные методы извлечения квадратного корня
(без использования калькулятора).
Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а 2 +b, где а 2 ближайший к числу х точный квадрат натурального числа а (а 2 ?х), и пользовались формулой 
Извлечем с помощью формулы (1) корень квадратный, например из числа 28:
Результат извлечения корня из 28 с помощью калькулятора 5,2915026. Как видим способ вавилонян дает хорошее приближение к точному значению корня.
Исаак Ньютон разработал метод извлечения квадратного корня, который восходил еще к Герону Александрийскому (около 100 г. н.э.). Метод этот (известный как метод Ньютона) заключается в следующем.
Пусть а1 — первое приближение числа 
Следующее, более точное приближение а2 числа 

Третье, еще более точное приближение 
(n+1)-е приближение 

Нахождение приближенного значения числа 


Указанный мною способ позволяет извлекать квадратный корень из большого числа с любой точностью, правда с существенным недостатком: громоздкость вычислений.
1. Пичугин Л.Ф. За страницами учебника алгебры.
Квадратный корень
Основные сведения
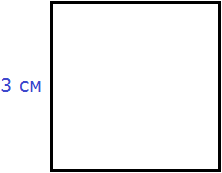
Чтобы найти площадь квадрата, нужно длину его стороны возвести во вторую степень.
Найдём площадь квадрата, длина стороны которого 3 см
S = 3 2 = 9 см 2
Теперь решим обратную задачу. А именно, зная площадь квадрата определим длину его стороны. Для этого воспользуемся таким инструментом как кóрень. Корень бывает квадратный, кубический, а также n-й степени.
Сейчас наш интерес вызывает квадратный корень. По другому его называют кóрнем второй степени.
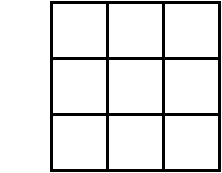
Для нахождения длины стороны нашего квадрата, нужно найти число, вторая степень которого равна 9. Таковым является число 3. Это число и является кóрнем.
Введём для работы с корнями новые обозначения.
Символ кóрня выглядит как 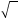
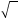
Под корнем располагáют подкореннóе выражение. В нашем случае подкоренным выражением будет число 9 (площадь квадрата)
Нас интересовал квадратный корень (он же корень второй степени), поэтому слева над корнем указываем число 2. Это число называют показателем корня (или степенью корня)
Получили выражение, которое читается так: « квадратный корень из числа 9» . С этого момента возникает новая задача по поиску самогó корня.
Если число 3 возвести во вторую степень, то получится число 9. Поэтому число 3 и будет ответом:
Значит квадрат площадью 9 см 2 имеет сторону, длина которой 3 см. Приведённое действие называют извлечéнием квадрáтного кóрня.
Нетрудно догадаться, что квадратным корнем из числа 9 также является отрицательное число −3. При его возведении во вторую степень тоже получается число 9
Получается, что выражение 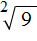
Вообще, квадратный корень имеет два противоположных значения: положительное и отрицательное.
Например, извлечём квадратный корень из числа 4
Это выражение имеет два значения: 2 и −2, поскольку при возведении этих чисел во вторую степень, получится один и тот же результат 4
Поэтому ответ к выражению вида 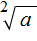
Запишем ответ к выражению 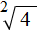
Определения
Дадим определение квадратному корню.
Квадратным корнем из числа a называют такое число b, вторая степень которого равна a .
То есть число b должно быть таким, чтобы выполнялось равенство b 2 = a . Число b (оно же корень) обозначается через радикал 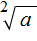
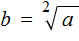
Например, квадратным корнем из числá 16 есть число 4, поскольку число 4 во второй степени равно 16
Корень 4 можно обозначить через радикал 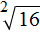

Также квадратным корнем из числá 16 есть число −4, поскольку число −4 во второй степени равно 16
Если при решении задачи интересует только положительное значение, то корень называют не просто квадратным, а арифметическим квадратным.
Арифметический квадратный корень из числá a — это неотрицательное число b (b ≥ 0) , при котором выполняется равенство b 2 = a .
В нашем примере квадратными корнями из числá 16 являются корни 4 и −4, но арифметическим из них является только корень 4.
В разговорном языке можно использовать сокращение. К примеру, выражение 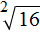
Не следует путать понятия корень и квадрат . Квадрат это число, которое получилось в результате возведения какого-нибудь числá во вторую степень. Например, числа 25, 36, 49 являются квадратами, потому что они получились в результате возведения во вторую степень чисел 5, 6 и 7 соответственно.
Корнями же являются числа 5, 6 и 7 . Они являются теми числами, которые во второй степени равны 25, 36 и 49 соответственно.
Чаще всего в квадратных корнях показатель кóрня вообще не указывается. Так, вместо записи 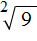
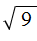
Квадратный корень из единицы равен единице. То есть справедливо следующее равенство:
Это по причине того, что единица во второй степени равна единице:
и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице:
Квадратный корень из нуля равен нулю. То есть справедливо равенство 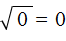
Выражение вида 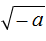
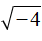
Если выражение вида 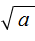
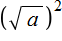
Например, выражение 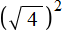
Это потому что выражение 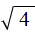
Корень из квадрата числá равен модулю этого числá:
Например, корень из числá 5, возведённого во вторую степень, равен модулю числá 5
Если во вторую степень возвóдится отрицательное число, ответ опять же будет положительным. Например, корень из числá −5 , возведённого во вторую степень, равен модулю числá −5. А модуль числа −5 равен 5
Действительно, если не пользуясь правилом 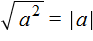
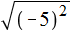
Не следует путать правило 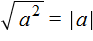
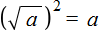
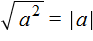
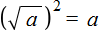
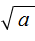
В некоторых учебниках знак корня может выглядеть без верхней линии. Выглядит это так:
Мéньшему числу соответствует мéньший корень, а бóльшему числу соответствует бóльший корень.
Например, рассмотрим числа 49 и 64. Число 49 меньше, чем число 64.
Если извлечь квадратные корни из этих чисел, то числу 49 будет соответствовать меньший корень, а числу 64 — бóльший. Действительно, √49 = 7 , а √64 = 8 ,
Примеры извлечения квадратных корней
Рассмотрим несколько простых примеров на извлечение квадратных корней.
Пример 1. Извлечь квадратный корень √36
Данный квадратный корень равен числу, квадрат которого равен 36. Таковым является число 6, поскольку 6 2 = 36
Пример 2. Извлечь квадратный корень √49
Данный квадратный корень равен числу, квадрат которого равен 49. Таковым является число 7, поскольку 7 2 = 49
В таких простых примерах достаточно знать таблицу умножения. Так, мы помним, что число 49 входит в таблицу умножения на семь. То есть:
Но 7 × 7 это 7 2
Пример 3. Извлечь квадратный корень √100
Данный квадратный корень равен числу, квадрат которого равен 100. Таковым является число 10 , поскольку 10 2 = 100
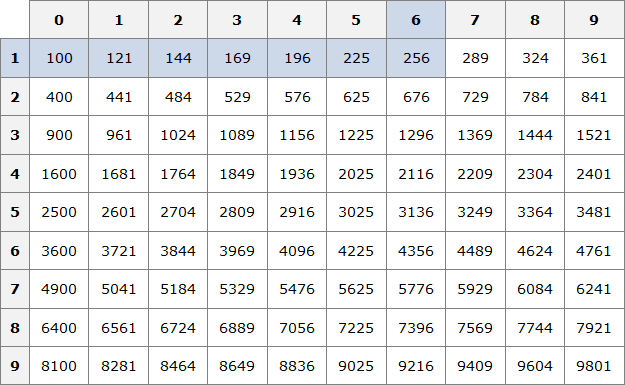
Число 100 это последнее число, корень которого можно извлечь с помощью таблицы умножения. Для чисел, бóльших 100, квадратные корни можно находить с помощью таблицы квадратов.
Пример 3. Извлечь квадратный корень √256
Данный квадратный корень равен числу, квадрат которого равен 256. Чтобы найти это число, воспользуемся таблицей квадратов.
Нахóдим в таблице квадратов число 256 и двигаясь от него влево и вверх определяем цифры, которые образуют число, квадрат которого равен 256.
Видим, что это число 16 . Значит √256 = 16 .
Пример 4. Найти значение выражения 2√16
В данном примере число 2 умножается на выражение с корнем. Сначала вычислим корень √16 , затем перемнóжим его с числом 2
Пример 7. Решить уравнение
В данном примере нужно найти значение переменной x, при котором левая часть будет равна 4.
Значение переменной x равно 16, поскольку 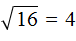
Примечание. Не следует путать корень уравнения и квадратный корень. Корень уравнения это значение переменной, при котором уравнение обращается в верное числовое равенство. А квадратный корень это число, вторая степень которого равна выражению, находящемуся под радикалом 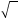
Подобные примеры решают, пользуясь определением квадратного корня. Давайте и мы поступим так же.
Из определения мы знаем, что квадратный корень 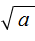
Применим равенство b 2 = a к нашему примеру 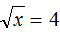
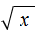
В выражении 4 2 = x вычислим левую часть, полýчим 16 = x . Поменяем левую и правую часть местами, полýчим x = 16 . В результате приходим к тому, что нашлось значение переменной x .
Пример 8. Решить уравнение
Перенесем −8 в правую часть, изменив знак:
Возведем правую часть во вторую степень и приравняем её к переменной x
Вычислим правую часть, полýчим 64 = x . Поменяем левую и правую часть местами, полýчим x = 64 . Значит корень уравнения 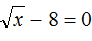
Пример 9. Решить уравнение
Воспользуемся определением квадратного корня:
Роль переменной b играет число 7, а роль переменной a — подкореннóе выражение 3 + 5x . Возведем число 7 во вторую степень и приравняем его к 3 + 5x
В выражении 7 2 = 3 + 5x вычислим левую часть полýчим 49 = 3 + 5x . Получилось обычное линейное уравнение. Решим его:
Корень уравнения 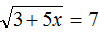
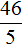
Пример 10. Найти значение выражения
В этом выражении число 2 умножается на квадратный корень из числа 49.
Сначала нужно извлечь квадратный корень и перемножить его с числом 2
Приближённое значение квадратного корня
Не каждый квадратный корень можно извлечь. Извлечь квадратный корень можно только в том случае, если удаётся найти число, вторая степень которого равна подкореннóму выражению.
Например, извлечь квадратный корень 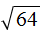
А извлечь квадратный корень 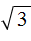
Зато можно извлечь квадратный корень из числа 3 приближённо. Извлечь квадратный корень приближённо означает найти значение, которое при возведении во вторую степень будет максимально близко к подкореннóму выражению.
Приближённое значение ищут с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и так далее.
Найдём значение корня 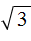
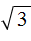
Для начала найдём ближайшее меньшее число, корень которого можно извлечь. Таковым является число 1. Корень из этого числа равен самому этому числу:
Аналогично находим ближайшее бóльшее число, корень которого можно извлечь. Таковым является число 4. Корень из этого числа равен 2
А √3 больше, чем √1 но меньше, чем √4. Запишем это в виде двойного неравенства:
Точные значения корней √1 и √4 известны. Это числа 1 и 2
Тогда очевидно, что значение корня √3 будет представлять собой десятичную дробь, потому что между числами 1 и 2 нет целых чисел.
Для нахождения приближённого значения квадратного корня √3 будем проверять десятичные дроби, располагающиеся в интервале от 1 до 2, возводя их в квадрат. Делать это будем до тех пор пока не полýчим значение, максимально близкое к 3. Проверим к примеру дробь 1,1
Получился результат 1,21, который не очень близок к подкореннóму выражению 3. Значит 1,1 не годится в качестве приближённого значения квадратного корня √3 , потому что оно малó.
Проверим тогда дробь 1,8
Получился результат 3,24, который близок к подкореннóму выражению, но превосходит его на 0,24. Значит 1,8 не годится в качестве приближенного значения корня √3 , потому что оно великó.
Проверим тогда дробь 1,7
Получился результат 2,89, который уже близок к подкореннóму выражению. Значит 1,7 и будет приближённым значением квадратного корня √3 . Напомним, что знак приближенного значения выглядит как ≈
Значение 1,6 проверять не нужно, потому что в результате получится число 2,56 , которое дальше от трёх, чем значение 2,89. А значение 1,8, как было показано ранее, является уже большим.
В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение можно получить ещё более точно. Для этого его следует находить с точностью до сотых.
Чтобы найти значение с точностью до сотых проверим десятичные дроби в интервале от 1,7 до 1,8
Проверим дробь 1,74
Получился результат 3,0276 , который близок к подкореннóму выражению, но превосходит его на 0,0276 . Значит значение 1,74 великó для корня √3 .
Проверим тогда дробь 1,73
Получился результат 2,9929 , который близок к подкореннóму выражению √3 . Значит 1,73 будет приближённым значением квадратного корня √3 с точностью до сотых.
Процесс нахождения приближённого значения квадратного корня продолжается бесконечно. Так, корень √3 можно находить с точностью до тысячных, десятитысячных и так далее:
√3 = 1,732 (вычислено с точностью до тысячных)
√3 = 1,7320 (вычислено с точностью до десятитысячных)
√3 = 1,73205 (вычислено с точностью до ста тысячных).
Ещё квадратный корень можно извлечь с точностью до целых. Приближённое значение квадратного корня √3 с точностью до целых равно единице:
Значение 2 будет слишком большим, поскольку при возведении этого числа во вторую степень получается число 4, которое больше подкоренного выражения. Нас же интересуют значения, которые при возведении во вторую степень равны подкореннóму выражению или максимально близки к нему, но не превосходят его.
В зависимости от решаемой задачи допускается находить значение, вторая степень которого больше подкоренного выражения. Это значение называют приближённым значением квадратного корня с избытком. Поговорим об этом подробнее.
Приближенное значение квадратного корня с недостатком или избытком
Иногда можно встретить задание, в котором требуется найти приближённое значение корня с недостатком или избытком.
В предыдущей теме мы нашли приближённое значение корня √3 с точностью до десятых с недостатком. Недостаток понимается в том смысле, что до значения 3 нам недоставало ещё некоторых частей. Так, найдя приближённое значение √3 с точностью до десятых, мы получили 1,7. Это значение является значением с недостатком, поскольку при возведении этого числа во вторую степень полýчим результат 2,89 . Этому результату недостаёт ещё 0,11 чтобы получить число 3. То есть, 2,89 + 0,11 = 3.
С избытком же называют приближённые значения, которые при возведении во вторую степень дают результат, который превосходит подкореннóе выражение. Так, вычисляя корень √3 приближённо, мы проверили значение 1,8. Это значение является приближённым значением корня √3 с точностью до десятых с избытком, поскольку при возведении 1,8 во вторую степень, получаем число 3,24 . Этот результат превосходит подкореннóе выражение на 0,24 . То есть 3,24 − 3 = 0,24 .
Приближённое значение квадратного корня √3 с точностью до целых тоже был найден с недостатком:
Это потому что при возведении единицы в квадрат получаем единицу. То есть до числа 3 недостаёт ещё 2.
Приближённое значение квадратного корня √3 с точностью до целых можно найти и с избытком. Тогда этот корень приближённо будет равен 2
Это потому что при возведении числа 2 в квадрат получаем 4. Число 4 превосходит подкореннóе выражение 3 на единицу. Извлекая приближённо квадратный корень с избытком желательно уточнять, что корень извлечен именно с избытком:
Потому что приближённое значение чаще всего ищется с недостатком, чем с избытком.
Дополнительно следует упомянуть, что в некоторых учебниках словосочетания «с точностью до целых», «с точностью до десятых», с «точностью до сотых» , заменяют на словосочетания «с точностью до 1» , «с точностью до 0,1» , «с точностью до 0,01» соответственно.
Так, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это значит что корень следует извлекать приближённо с точностью до сотых:
Пример 2. Извлечь квадратный корень из числа 51 с точностью до 1
Пример 3. Извлечь квадратный корень из числа 51 с точностью до 0,1
Пример 4. Извлечь квадратный корень из числа 51 с точностью до 0,01
Границы, в пределах которых располагаются корни
Если исходное число принадлежит промежутку [1; 100], то квадратный корень из этого исходного числа будет принадлежать промежутку [1; 10].
Например, пусть исходным числом будет 64 . Данное число принадлежит промежутку [1; 100] . Сразу делаем вывод, что квадратный корень из числа 64 будет принадлежать промежутку [1; 10] . Теперь вспоминаем таблицу умножения. Какое перемножение двух одинаковых сомножителей даёт в результате 64 ? Ясно, что перемножение 8 × 8 , а это есть 8 2 = 64 . Значит квадратный корень из числа 64 есть 8
Пример 2. Извлечь квадратный корень из числа 49
Число 49 принадлежит промежутку [1; 100] . Значит квадратный корень будет принадлежать промежутку [1; 10] . Этим корнем будет число 7 , поскольку 7 2 = 49
Пример 2. Извлечь квадратный корень из числа 1
Число 1 принадлежит промежутку [1; 100] . Значит квадратный корень будет принадлежать промежутку [1; 10] . Этим корнем будет число 1, поскольку 1 2 = 1
Пример 3. Извлечь квадратный корень из числа 100
Число 100 принадлежит промежутку [1; 100] . Значит квадратный корень будет принадлежать промежутку [1; 10] . Этим корнем будет число 10, поскольку 10 2 = 100
Понятно, что промежуток [1; 100] содержит ещё и числа, квадратные корни из которых не извлекаются. Для таких чисел корень нужно извлекать приближённо. Тем не менее, приближённый корень тоже будет располагаться в пределах промежутка [1; 10] .
Например, извлечём квадратный корень из числа 37 . Нет целого числа, вторая степень которого была бы равна 37 . Поэтому извлекать квадратный корень следует приближённо. Извлечём его к примеру с точностью до сотых:
Для облегчения можно находить ближайшее меньшее число, корень из которого извлекается. Таковым в данном примере было число 36 . Квадратный корень из него равен 6 . И далее отталкиваясь от числа 6 , можно находить приближённое значение корня √37 , проверяя различные десятичные дроби, целая часть которых равна 6 .
Квадраты чисел от 1 до 10 обязательно нужно знать наизусть. Ниже представлены эти квадраты:
1 2 = 1
2 2 = 4
3 2 = 9
4 2 = 16
5 2 = 25
6 2 = 36
7 2 = 49
8 2 = 64
9 2 = 81
10 2 = 100
И обратно, следует знать значения квадратных корней этих квадратов:
Если к любому числу от 1 до 10 в конце дописать ноль (или несколько нулей), и затем возвести это число во вторую степень, то в полученном числе будет в два раза больше нулей.
Например, 6 2 = 36 . Допишем к числу 6 один ноль, полýчим 60 . Возведём число 60 во вторую степень, полýчим 3600
А если к числу 6 дописать два нуля, и возвести это число во вторую степень, то полýчим число, в котором четыре нуля. То есть в два раза больше нулей:
Тогда можно сделать следующий вывод:
Если исходное число содержит знакомый нам квадрат и чётное количество нулей, то можно извлечь квадратный корень из этого числа. Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа.
Например, извлечём квадратный корень из числа 900 . Видим, что в данном числе есть знакомый нам квадрат 9 . Извлекаем из него корень, получаем 3
Теперь из исходного числа записываем половину от количества нулей. В исходном числе 900 содержится два нуля. Половина этого количества нулей есть один ноль. Записываем его в ответе после цифры 3
Пример 2. Извлечём квадратный корень из числа 90000
Здесь опять же имеется знакомый нам квадрат 9 и чётное количество нулей. Извлекаем корень из числа 9 и записываем половину от количества нулей. В исходном числе содержится четыре нуля. Половиной же этого количества нулей будет два нуля:
Пример 3. Извлечем квадратный корень из числа 36000000
Здесь имеется знакомый нам квадрат 36 и чётное количество нулей. Извлекаем корень из числа 36 и записываем половину от количества нулей. В исходном числе шесть нулей. Половиной же будет три нуля:
Пример 4. Извлечем квадратный корень из числа 2500
Здесь имеется знакомый нам квадрат 25 и чётное количество нулей. Извлекаем корень из числа 25 и записываем половину от количества нулей. В исходном числе два нуля. Половиной же будет один ноль:
Если подкореннóе число увеличить (или уменьшить) в 100, 10000 то корень увеличится (или уменьшится) в 10, 100 раз соответственно.
Например, 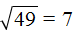
И наоборот, если в равенстве 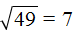
Пример 2. Увеличим в равенстве 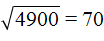
Пример 3. Уменьшим в равенстве 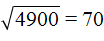
Эта закономерность позволяет извлечь квадратный корень из десятичной дроби, если в данной дроби после запятой содéржатся две цифры, и эти две цифры образуют знакомый нам квадрат. В таких случаях данную десятичную дробь следует умножить на 100 . Затем извлечь квадратный корень из получившегося числа и уменьшить подкореннóе число в сто раз.
Например, извлечём квадратный корень из числа 0,25 . В данной десятичной дроби после запятой содержатся две цифры и эти две цифры образуют знакомый нам квадрат 25.
Умнóжим десятичную дробь 0,25 на 100, полýчим 25. А из числа 25 квадратный корень извлекается легко:
Но нам изначально нужно было извлечь корень из 0,25, а не из 25. Чтобы исправить ситуацию, вернём нашу десятичную дробь. Если в равенстве 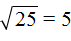
Обычно в таких случаях достаточно уметь передвигáть запятую. Потому что сдвинуть в числе запятую вправо на две цифры это всё равно что умножить это число на 100 .
В предыдущем примере в подкоренном числе 0,25 можно было сдвинуть запятую вправо на две цифры, а в полученном ответе сдвинуть её влево на одну цифру.
Например, извлечем корень из числа 0,81. Мысленно передвинем запятую вправо на две цифры, полýчим 81. Теперь извлечём квадратный корень из числа 81, полýчим ответ 9. В ответе 9 передвинем запятую влево на одну цифру, полýчим 0,9. Значит, 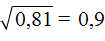
Это правило работает и в ситуации, когда после запятой содержатся четыре цифры и эти цифры образуют знакомый нам квадрат.
Например, десятичная дробь 0,1225 содержит после запятой четыре цифры. Эти четыре цифры образуют число 1225 , квадратный корень из которого равен 35 .
Тогда можно извлечь квадратный корень и из 0,1225 . Умнóжим данную десятичную дробь на 10000 , полýчим 1225 . Из числа 1225 квадратный корень можно извлечь с помощью таблицы квадратов:
Но нам изначально нужно было извлечь корень из 0,1225 , а не из 1225 . Чтобы исправить ситуацию, в равенстве 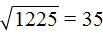
Эта же закономерность будет работать и при извлечении корней из дробей вида 12,25 . Если цифры из которых состоит десятичная дробь образуют знакомый нам квадрат, при этом после запятой содержится чётное количество цифр, то можно извлечь корень из этой десятичной дроби.
Умнóжим десятичную дробь 12,25 на 100 , полýчим 1225 . Извлечём корень из числа 1225
Теперь в равенстве 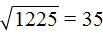
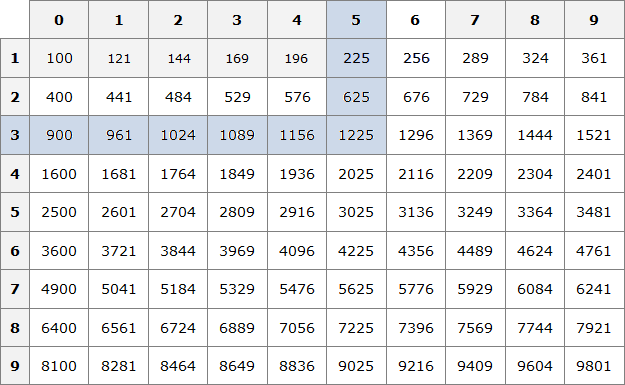
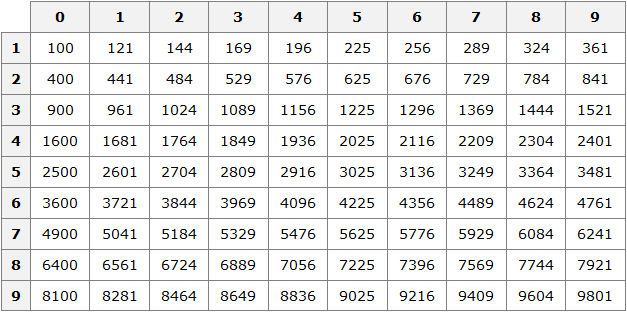
Если исходное число принадлежит промежутку [100; 10000], то квадратный корень из этого исходного числа будет принадлежать промежутку [10; 100].
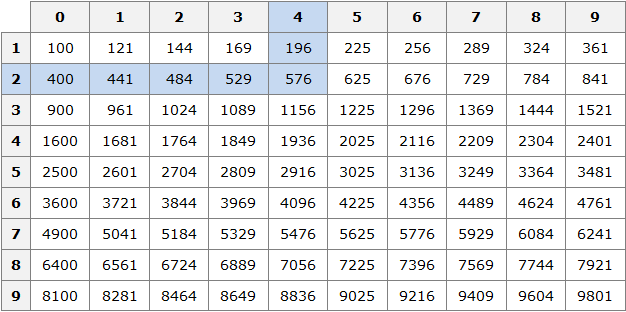
В этом случае применяется таблица квадратов:
Например, пусть исходным числом будет 576. Данное число принадлежит промежутку [100; 10000] . Сразу делаем вывод, что квадратный корень из числа 576 будет принадлежать промежутку [10; 100] . Теперь открываем таблицу квадратов и смотрим какое число во второй степени равно 576
Видим, что это число 24. Значит 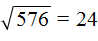
Пример 2. Извлечь квадратный корень из числа 432 .
Число 432 принадлежит промежутку [100; 10000] . Значит квадратный корень следует искать в промежутке [10; 100] . Открываем таблицу квадратов и смотрим какое число во второй степени равно 432. Обнаруживаем, что число 432 в таблице квадратов отсутствует. В этом случае квадратный корень следует искать приближённо.
Извлечем квадратный корень из числа 432 с точностью до десятых.
В таблице квадратов ближайшее меньшее число к 432 это число 400. Квадратный корень из него равен 20. Отталкиваясь от числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20.
Проверим, например, число 20,8. Для этого возведём его в квадрат:
Получилось число 432,64 которое превосходит исходное число 432 на 0,64. Видим, что значение 20,8 великó для корня √432 . Проверим тогда значение 20,7
Значение 20,7 годится в качестве корня, поскольку в результате возведения этого числа в квадрат получается число 428,49 , которое меньше исходного числа 432 , но близко к нему. Значит √432 ≈ 20,7 .
Необязательно запоминать промежутки чтобы узнать в каких границах располагается корень. Можно воспользоваться методом нахождения ближайших квадратов с чётным количеством нулей на конце.
Например, извлечём корень из числа 4225 . Нам известен ближайший меньший квадрат 3600 , и ближайший больший квадрат 4900
Извлечём квадратные корни из чисел 3600 и 4900. Это числа 60 и 70 соответственно:
Тогда можно понять, что квадратный корень из числа 4225 располагается между числами 60 и 70 . Можно даже найти его методом подбора. Корни 60 и 70 исключаем сразу, поскольку это корни чисел 3600 и 4900 . Затем можно проверить, например, корень 64 . Возведём его в квадрат (или умнóжим данное число само на себя)
Корень 64 не годится. Проверим корень 65
Получается 4225. Значит 65 является корнем числа 4225
Тождественные преобразования с квадратными корнями
Над квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований.
Квадратный корень из произведения
Квадратный корень из произведения это выражение вида 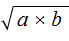
Например, выражение 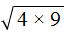
Чтобы извлечь такой квадратный корень, нужно по отдельности извлечь квадратные корни из множителей 4 и 9, представив выражение 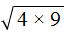
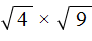
Конечно, можно не прибегать к таким манипуляциям, а вычислить сначала подкореннóе выражение 4 × 9 , которое равно 36 . Затем извлечь квадратный корень из числа 36
Но при извлечении квадратных корней из больших чисел это правило может оказаться весьма полезным.
Допустим, потребовалось извлечь квадратный корень из числа 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12
Но предстáвим, что таблицы квадратов под рукой не оказалось. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются.
Итак, разлóжим число 144 на простые множители:
Получили следующее разложение:
В разложéнии содержатся четыре двойки и две тройки. При этом все числа, входящие в разложение, перемнóжены. Это позволяет предстáвить произведения одинаковых сомножителей в виде степени с показателем 2.
Тогда четыре двойки можно заменить на запись 2 2 × 2 2 , а две тройки заменить на 3 2
В результате будем иметь следующее разложение:
Теперь можно извлекáть квадратный корень из разложения числа 144
Применим правило извлечения квадратного корня из произведения:
Ранее было сказано, что если подкореннóе выражение возведенó во вторую степень, то такой квадратный корень равен модулю из подкореннóго выражения.
Тогда получится произведение 2 × 2 × 3 , которое равно 12
Простые множители представляют в виде степени для удобства и короткой записи. Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители.
Так, разложив число 144 на простые множители, мы получили разложение 2 × 2 × 2 × 2 × 3 × 3 . Это разложение можно записать под кóрнем как есть:
затем перемнóжить некоторые сомножители так, чтобы получились числа, квадратные корни из которых извлекаются. В данном случае можно дважды перемнóжить две двойки и один раз перемнóжить две тройки:
Затем применить правило извлечения квадратного корня из произведения и получить окончательный ответ:
С помощью правила извлечения квадратного корня из произведения можно извлекать корень и из других больших чисел. В том числе, из тех чисел, которых нет в таблице квадратов.
Например, извлечём квадратный корень из числа 13456 . Этого числа нет в таблице квадратов, поэтому воспользуемся правилом извлечения квадратного корня из произведения, предварительно разложив число 13456 на простые множители.
Итак, разложим число 13456 на простые множители:
В разложении имеются четыре двойки и два числа 29. Двойки дважды предстáвим как 2 2 . А два числа 29 предстáвим как 29 2 . В результате полýчим следующее разложение числа 13456
Теперь будем извлекать квадратный корень из разложения числа 13456
Итак, если a ≥ 0 и b ≥ 0 , то 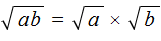
Докажем равенство 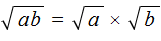
Согласно определению, квадратным корня из числа a есть число b , при котором выполняется равенство b 2 = a .
В нашем случае нужно удостовериться, что правая часть равенства 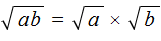
Итак, выпишем правую часть равенства 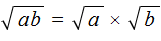
Теперь воспользуемся правилом возведения в степень произведения. Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень:
Ранее было сказано, что если выражение вида 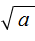
Значит равенство 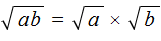
Правило извлечения квадратного корня из произведения работает и в случае, если под кóрнем располагается более двух множителей. То есть справедливым будет следующее равенство:
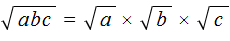
Пример 1. Найти значение квадратного корня
Запишем корень 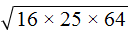
Пример 2. Найти значение квадратного корня
Предстáвим число 250 в виде произведения чисел 25 и 10 . Делать это будем под знáком корня:
Теперь под кóрнем образовалось два одинаковых множителя 10 и 10. Перемнóжим их, полýчим 100
Далее применяем правило извлечения квадратного кóрня из произведения и получáем окончательный ответ:
Пример 3. Найти значение квадратного корня
Воспользуемся правилом возведения степени в степень. Степень 11 4 предстáвим как (11 2 ) 2 .
Теперь воспользуемся правилом извлечения квадратного кóрня из квадрата числа:
В нашем случае квадратный корень из числа (11 2 ) 2 будет равен 11 2 . Говоря простым языком, внешний показатель степени 2 исчезнет, а внутренний останется:
Далее возводим число 11 во вторую степень и получаем окончательный ответ:
Этот пример также можно решить, воспользовавшись правилом извлечения квадратного корня из произведения. Для этого подкореннóе выражение 11 4 нужно записать в виде произведения 11 2 × 11 2 . Затем извлечь квадратный корень из этого произведения:
Пример 4. Найти значение квадратного корня
Перепишем степень 3 4 в виде (3 2 ) 2 , а степень 5 6 в виде (5 3 ) 2
Далее используем правило извлечения квадратного кóрня из произведения:
Далее используем правило извлечения квадратного кóрня из квадрата числа:
Вычислим произведение получившихся степеней и полýчим окончательный ответ:
Сомножители, находящиеся под корнем, могут быть десятичными дробями. Например, извлечём квадратный корень из произведения
Запишем корень 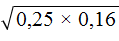
Пример 6. Найти значение квадратного корня
Пример 7. Найти значение квадратного корня
Если первый сомножитель умножить на число n , а второй сомножитель разделить на это число n , то произведение не изменится.
Например, произведение 8 × 4 равно 32
Умнóжим сомножитель 8 скажем на число 2 , а сомножитель 4 раздéлим на это же число 2. Тогда получится произведение 16 × 2 , которое тоже равно 32 .
Это свойство полезно при решении некоторых задач на извлечение квадратных корней. Сомножители подкореннóго выражения можно умнóжить и разделить так, чтобы корни из них извлекались.
Например, извлечём квадратный корень из произведения 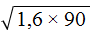
Проанализировав подкореннóе выражение 1,6 × 90 , можно заметить, что если первый сомножитель 1,6 умножить на 10 , а второй сомножитель 90 разделить на 10 , то полýчится произведение 16 × 9 . Из такого произведения квадратный корень можно извлечь, пользуясь правилом извлечения квадратного корня из произведения.
Запишем полное решение данного примера:
Процесс умножения и деления можно выполнять в уме. Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче:
Пример 9. Найти значение квадратного корня
Умнóжим первый сомножитель на 10 , а второй раздéлим на 10 . Тогда под кóрнем образуется произведение 36 × 0,04 , квадратный корень из которого извлекается:
Если в равенстве 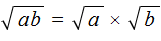
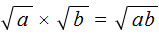
Например, узнáем чему равно значение выражения 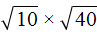
Квадратные корни из чисел 10 и 40 не извлекаются. Воспользуемся правилом 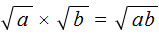
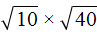
Теперь найдём значение произведения, находящегося под корнем:
А квадратный корень из числа 400 извлекается. Он равен 20
Сомножители, располагáющиеся под корнем, можно расклáдывать на множители, группировáть, представлять в виде степени, а также перемножáть для получения новых сомножителей, корни из которых извлекаются.
Например, найдём значение выражения 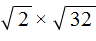
Воспользуемся правилом
Сомножитель 32 это 2 5 . Предстáвим этот сомножитель как 2 × 2 4
Перемнóжим сомножители 2 и 2, полýчим 4. А сомножитель 2 4 предстáвим в виде степени с показателем 2
Теперь воспóльзуемся правилом 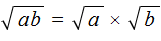
Пример 12. Найти значение выражения
Воспользуемся правилом
Сомножитель 8 это 2 × 2 × 2 , а сомножитель 98 это 2 × 7 × 7
Теперь под кóрнем имеются четыре двойки и две семёрки. Четыре двойки можно записать как 2 2 × 2 2 , а две семёрки как 7 2
Теперь воспользуемся правилом 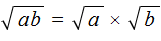
Квадратный корень из дроби
Квадратный корень вида 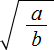
Например, квадратный корень из дроби 
Вычислим квадратные корни в числителе и знаменателе:
Значит, квадратный корень из дроби 
Докáжем, что равенство 
Возведём правую часть во вторую степень. Если в результате полýчим дробь 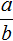

Пример 1. Извлечь квадратный корень
Воспользуемся правилом извлечения квадратного корня из дроби:
Пример 2. Извлечь квадратный корень
Переведём подкореннóе выражение в неправильную дробь, затем воспользуемся правилом извлечения квадратного корня из дроби:
Пример 3. Извлечь квадратный корень
Квадратным корнем из числа 0,09 является 0,3 . Но можно извлечь этот корень, воспользовавшись правилом извлечения квадратного корня из дроби.
Предстáвим подкоренное выражение в виде обыкновенной дроби. 0,09 это девять сотых:
Теперь можно воспользоваться правилом извлечения квадратного корня из дроби:
Пример 4. Найти значение выражения
Извлечём корни из 0,09 и 0,25, затем сложим полученные результаты:
Также можно воспользоваться правилом извлечения квадратного корня из дроби:
В данном примере первый способ оказался проще и удобнее.
Пример 5. Найти значение выражения
Сначала вычислим квадратный корень, затем перемнóжим его с 10. Получившийся результат вычтем из 4
Пример 6. Найти значение выражения
Сначала найдём значение квадратного корня 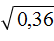
Теперь вычислим получившееся выражение. Согласно порядку действий, сначала надо выполнить умножение, затем сложение:
Вынесение множителя из-под знака корня
В некоторых задачах может быть полезным вынесение множителя из-под знака корня.
Рассмотрим квадратный корень из произведения 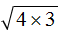
В нашем примере квадратный корень извлекается только из множителя 4. Его мы извлечём, а выражение 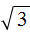
Это и есть вынесение множителя из-под знака корня.
На практике подкореннóе выражение чаще всего требуется разложить на множители.
Пример 2. Вынести множитель из-под знака корня в выражении
Разлóжим подкореннóе выражение на множители 9 и 2. Тогда полýчим:
Теперь воспользуемся правило извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 9. Множитель 2 остáвим под кóрнем:
Пример 3. Вынести множитель из-под знака корня в выражении
Разлóжим подкореннóе выражение на множители 121 и 3. Тогда полýчим:
Теперь воспользуемся правилом извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 121. Выражение √3 остáвим под корнем:
Пример 4. Вынести множитель из-под знака корня в выражении
Воспользуемся правилом извлечения квадратного корня из произведения:
Квадратный корень извлекается только из числа 121. Извлечём его, а выражение √15 оставим без изменений:
Получается, что множитель 11 вынесен из-под знака корня. Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √ 15 и 11 местами:
Пример 5. Вынести множитель из-под знака корня в выражении
Разлóжим подкореннóе выражение на множители 4 и 3
Воспользуемся правилом извлечения квадратного корня из произведения:
Извлечём корень из числа 4, а выражение √3 остáвим без изменений:
Пример 6. Упростить выражение
Предстáвим второе слагаемое 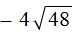
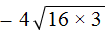
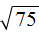
Теперь в выражениях 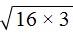
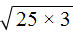
Во втором слагаемом 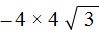
Замечáем, что получившемся выражении квадратный корень √3 является общим множителем. Вынесем его за скобки:
Вычислим содержимое скобок, полýчим −1
Если множителем является −1, то записывают только минус. Единица опускается. Тогда полýчим окончательный ответ −√3
Внесение множителя под знак корня
Рассмотрим следующее выражение:
В этом выражении число 5 умнóжено на квадратный корень из числа 9. Найдём значение этого выражения.
Сначала извлечём квадратный корень, затем перемнóжим его с числом 5.
Квадратный корень из 9 равен 3. Перемнóжим его с числом 5. Тогда полýчим 15
Число 5 в данном случае было множителем. Внесём этот множитель под знак корня. Но сделать это нужно таким образом, чтобы в результате наших действий значение исходного выражения не изменилось. Проще говоря, после внесения множителя 5 под знак корня, получившееся выражение по-прежнему должно быть равно 15.
Значение выражения не изменится, если число 5 возвести во вторую степень и только тогда внести его под корень:
Итак, если данó выражение 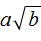
Пример 1. Внести множитель под знак корня в выражении
Возведём число 7 во вторую степень и внесём его под знак корня:
Пример 2. Внести множитель под знак корня в выражении
Возведём число 10 во вторую степень и внесем его под знак корня:
Пример 3. Внести множитель под знак корня в выражении
Вносить под знак корня можно только положительный множитель. Ранее было сказано, что выражение вида 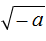
Однако, если перед знаком кóрня располагается отрицательный множитель, то минус можно оставить за знáком корня, а самó число внести под знак корня.
Пример 4. Внести множитель по знак корня в выражении
В этом примере под знак корня внóсится только 3. Минус остаётся за знáком корня:
Пример 5. Выполнить возведéние в степень в следующем выражении:
Воспользуемся формулой квадрата суммы двух выражений:
Роль переменной a в данном случае играет выражение √3 , роль переменной b — выражение √2 . Тогда полýчим:
Теперь необходимо упростить получившееся выражение.
Для выражений 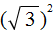
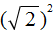
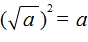
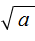
А в выражении 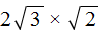
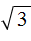
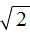
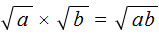
Приведём подобные слагаемые. В данном случае можно сложить слагаемые 3 и 2. А в слагаемом 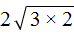
http://infourok.ru/priblizhennie-metodi-izvlecheniya-kvadratnogo-kornya-bez-ispolzovaniya-kalkulyatora-1171721.html
http://spacemath.xyz/kvadratnyj-koren/