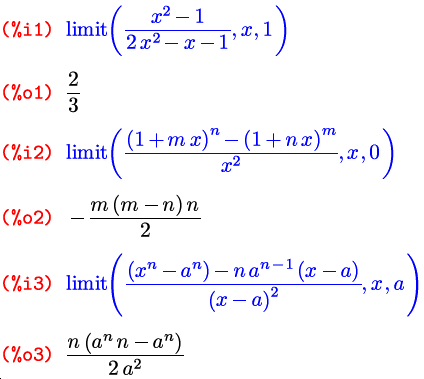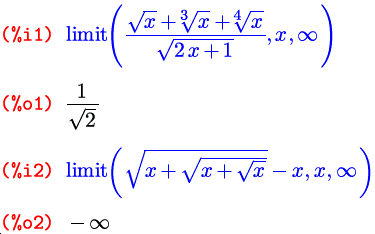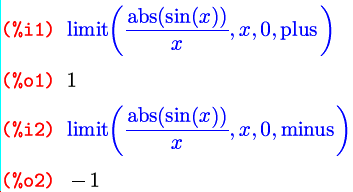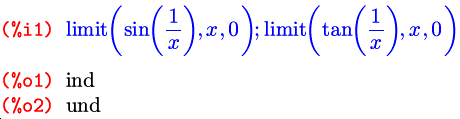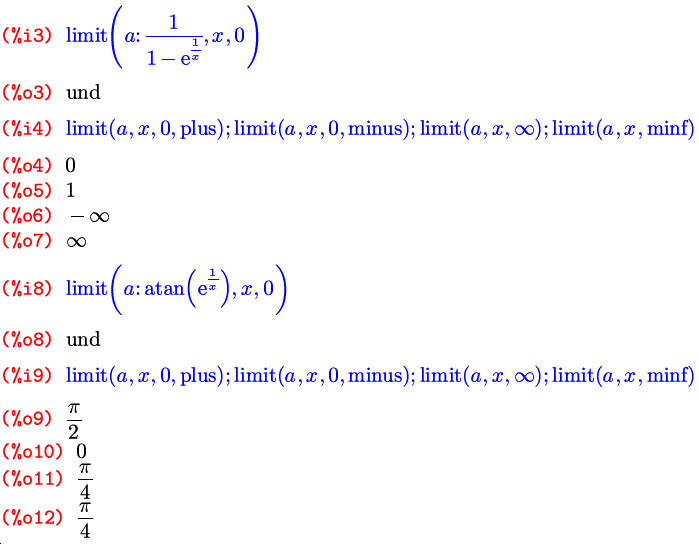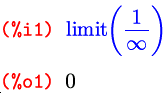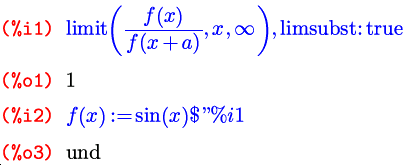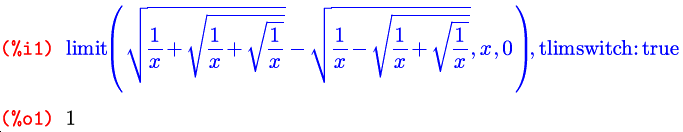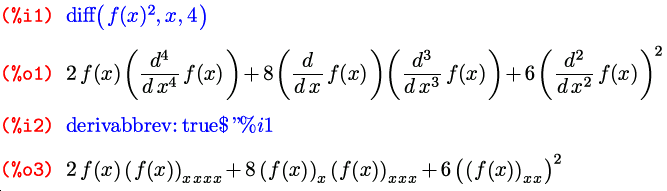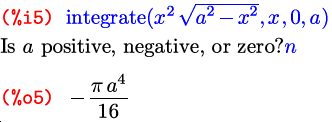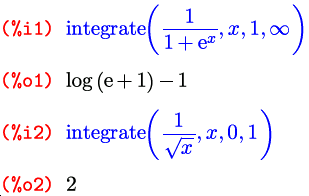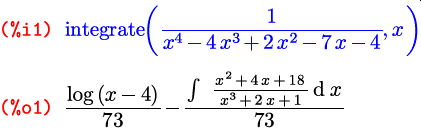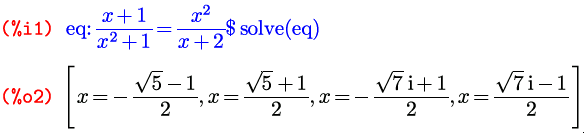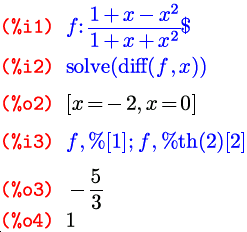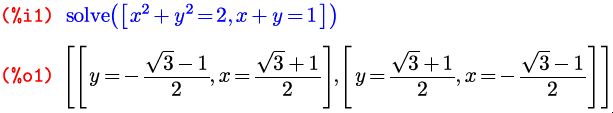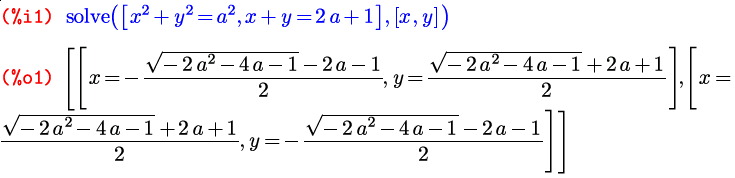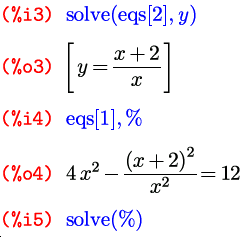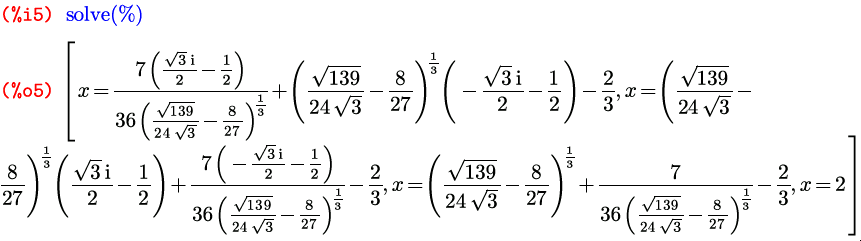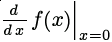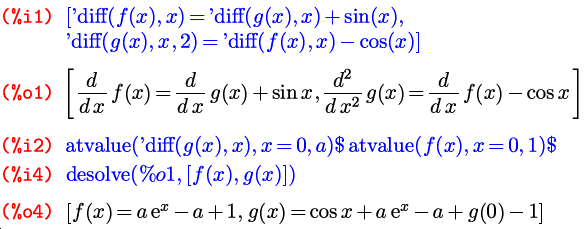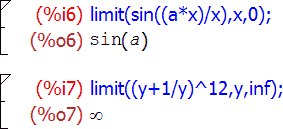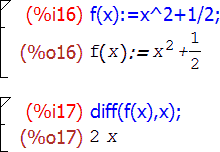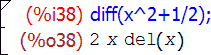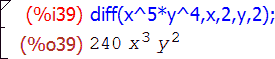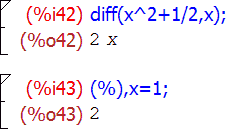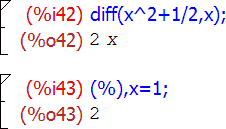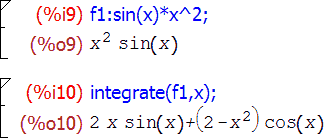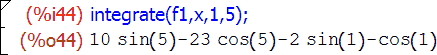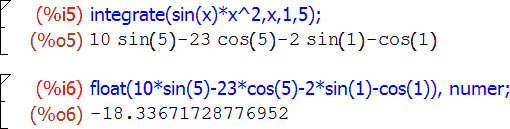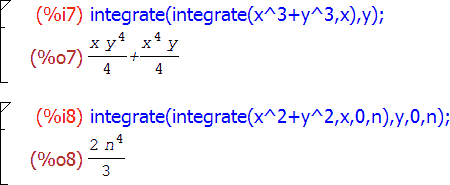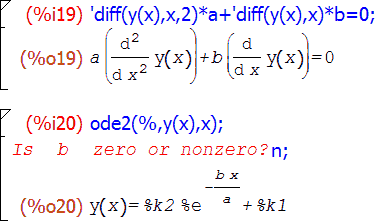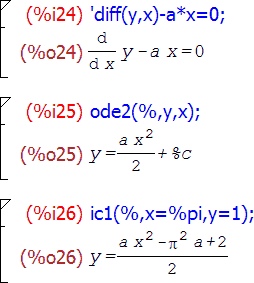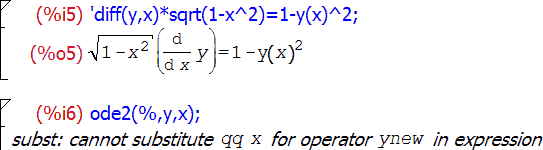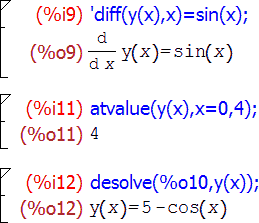Приближенное значение корней уравнения maxima

«Компьютерная математика с Maxima Руководство для школьников и студентов Е.А. Чичкарёв Москва ALT Linux 2012 УДК 519.67 ББК 22.1 Ч-72 Компьютерная математика с Maxima: . »

Глава Реализация некоторых численных методов 8.1 Программирование методов решения нелинейных уравнений в Maxima Необходимость отыскания корней нелинейных уравнений встречается в целом ряде задач: расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.

Пусть дано нелинейное уравнение f (x) = 0, и необходимо решить это уравнение, т. е. найти его корень x.

Если функция имеет вид многочлена степени m, f (x) = a0 xm + a1 xm1 + a2 xm2 +. + am1 x + am, где ai коэффициенты многочлена, i = 1, m, то уравнение f (x) = 0 имеет m корней (основная теорема алгебры).

Если функция f (x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x, то уравнение f (x) = 0 называется трансцендентным уравнением. Такие уравнения обычно имеют бесконечное множество решений.

Как известно, не всякое уравнение может быть решено точно. В первую очередь это относится к большинству трансцендентных уравнений.

8.1. Программирование методов решения нелинейных уравнений Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.

Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности. Для этого используются приближенные (численные) методы решения.

Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a, b], в котором лежит уточняемый корень уравнения.

Процесс определения интервала изоляции [a, b], содержащего только один из корней уравнения, называется отделением этого корня.

Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f (x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a, b] и на его концах имеет различные знаки, т.е. f (a)·f (b) 0, то между точками a и b имеется хотя бы один корень уравнения f (x) = 0. Если при этом функция f (x) на отрезке [a, b] монотонна, то указанный корень единственный.

Процесс определения корней алгебраических и трансцендентных уравнений состоит из двух этапов:

• отделение корней, т.е. определение интервалов изоляции [a, b], внутри которого лежит каждый корень уравнения;

• уточнение корней, т.е. сужение интервала [a, b] до величины равной заданной степени точности.

Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:

• метод половинного деления (метод дихотомии);

• метод простых итераций;

• метод Ньютона (метод касательных);

• модифицированный метод Ньютона (метод секущих);

• метод хорд и др.

8.1.1 Метод половинного деления Рассмотрим следующую задачу: дано нелинейное уравнение f (x) = 0, необходимо найти корень уравнения, принадлежащий интервалу [a, b], с заданной точностью.

Для уточнения корня методом половинного деления последовательно осуществляем следующие операции:

• вычисляем значение функции f (x) в точках a и t = (a + b)/2;

• если f (a) · f (t) 0, то корень находится в левой половине интервала [a, b], поэтому отбрасываем правую половину интервала и • если условие f (a) · f (t) 0 не выполняется, то корень находится в правой половине интервала [a, b], поэтому отбрасываем левую половину интервала [a, b] за счёт присваивания a = t.

В обоих случаях новый интервал [a, b] в 2 раза меньший предыдущего.

Процесс сокращения длины интервала неопределённости циклически повторяется до тех пор, пока длина интервала [a, b] не станет равной либо меньшей заданной точности, т.е. |b a|.

Реализация метода половинного деления в виде функции Maxima представлена в следующем примере:

• собственно функция bisect, в которую передаётся выражение f, определяющее уравнение, которое необходимо решить (%i1) bisect(f,sp,eps):=block([a,b],a:sp[1],b:sp[2],p:0, while abs(b-a)eps do ( fa:float(subst(a,x,f)), fc:float(subst(c,x,f)), (%o1) bisect (f, sp, eps) := block([a, b], a : sp1, b : sp2, p : 0, 8.1. Программирование методов решения нелинейных уравнений • последовательность команд, организующая обращение к bisect и результаты вычислений (%i2) f:exp(-x)-x$ a:-1$ b:2$ eps:0.000001$ xrez:bisect(f,[-2,2],eps)$ print(«Решение «,xrez,» Невязка «,subst(xrez,x,f))$ Решение 0.56714344024658 Невязка 2. (%o2) 2. В представленном примере решается уравнение ex x = 0. Поиск корня осуществляется на отрезке [2, 2] с точностью 0.000001.

Следует отметить особенность программирования для Maxima, заключающуюся в том, что решаемое уравнение задаётся в виде математического выражения (т.е. фактически текстовой строки). Числовое значение невязки уравнения вычисляется при помощи функции subst, посредством которой выполняется подстановка значений x = a или x = c в заданное выражение. Вычисление невязки после решения осуществляется также путём подстановки результата решения xrez в выражение f.

8.1.2 Метод простых итераций В ряде случаев весьма удобным приёмом уточнения корня уравнения является метод последовательных приближений (метод итераций).

Пусть с точностью необходимо найти корень уравнения f (x) = 0, принадлежащий интервалу изоляции [a, b]. Функция f (x) и ее первая производная непрерывны на этом отрезке.

Для применения этого метода исходное уравнение f (x) = 0 должно быть приведено к виду x = (x).

В качестве начального приближения может быть выбрана любая точка интервала [a, b].

Далее итерационный процесс поиска корня строится по схеме:

320 Глава 8. Реализация некоторых численных методов В результате итерационный процесс поиска реализуется рекуррентной формулой. Процесс поиска прекращается, как только выполняется условие |xn xn1 | или число итераций превысит заданное число N.

Для того, чтобы последовательность x1, x2. xn приближалась к искомому корню, необходимо, чтобы выполнялось условие сходимости | (x)| 1.

Пример реализации метода итераций представлен ниже:

(%i1) f:exp(-x)-x$ beta:0.1$ x1:1$ x0:0$ eps:0.000001$ p:0$ while abs(x1-x0)eps do (x0:x1, p:p+1, x1:float(x0+beta*(subst(x0,x,f))))$ print(«Число итераций «,p,» «,»Решение «,float(x1), » Невязка «,float(abs(x1-x0)))$ Число итераций 67 Решение 0. Невязка 9. 8.1.3 Метод Ньютона (метод касательных) Рассмотренные ранее методы решения нелинейных уравнений являются методами прямого поиска. В них для нахождения корня используется нахождение значения функции в различных точках интервала [a, b].

Метод Ньютона относится к градиентным методам, в которых для нахождения корня используется значение производной.

Рассмотрим нелинейное уравнение f (x) = 0, для которого необходимо найти корень на интервале [a,b] с точностью.

Метод Ньютона основан на замене исходной функции f (x), на каждом шаге поиска касательной, проведённой к этой функции. Пересечение касательной с осью X дает приближение корня.

Выберем начальную точку x0 = b (конец интервала изоляции). Находим значение функции в этой точке и проводим к ней касательную, пересечение которой с осью X дает первое приближение корня x1 :

8.1. Программирование методов решения нелинейных уравнений В результате, итерационный процесс схождения к корню реализуется рекуррентной формулой Процесс поиска продолжаем до тех пор, пока не выполнится услоf (xn ) Метод обеспечивает быструю сходимость, если выполняется условие: f (x0 ) · f (x0 ) 0, т.е. первую касательную рекомендуется проводить в той точке интервала [a, b], где знаки функции f (x0 ) и ее кривизны f (x0 ) совпадают.

Пример реализации метода Ньютона в Maxima представлен ниже:

(%i1) newton(f,x0,eps):=block([df,xn,xn0,r,p], xn0:x0, df:diff(f,x), while abs(r)eps do ( p:p+1, xn:xn0-float(subst(xn0,x,f)/subst(xn0,x,df)), print(«x0,x1 «,xn0,xn),r:xn-xn0, xn0:xn Последовательность команд для обращения к функции newton и результаты вычислений представлены в следующем примере:

(%i2) f:exp(-x)-x$ eps:0.000001$ xrez:newton(f,1,eps)$ print(«Решение «,xrez[1],» Число итераций «,xrez[2], » Невязка «,subst(xrez[1],x,f))$ x0, x1 1. x0, x1 0.53788284273999 0. x0, x1 0.56698699140541 0. x0, x1 0.56714328598912 0. Решение 0.56714329040978 Число итераций 4 Невязка 0. Особенности приведённого примера промежуточная печать результатов и возвращаемое значение в виде списка, что позволяет одновременно получить как значение корня, так и необходимое для достижения заданной точности число итераций. Существенному уменьшению числа итераций способствует и аналитическое вычисление производной.

322 Глава 8. Реализация некоторых численных методов 8.1.4 Модифицированный метод Ньютона (метод В этом методе для вычисления производных на каждом шаге поиска используется численное дифференцирование по формуле:

Тогда рекуррентная формула метода Ньютона приобретёт вид:

Реализация данного метода в Maxima представлено ниже:

(%i1) secant(f,sp,eps):=block([x0,x1,d,y,r], x0:sp[1],x1:sp[2], p:0, r:x1-x0, d:float(subst(x0,x,f)), while abs(r)eps do ( p:p+1, y:float(subst(x1,x,f)), r:r/(d-y)*y, (%i2) f:exp(-x)-x$ eps:0.000001$ xrez:secant(f,[-2,2],eps)$ print(«Решение «,xrez,» Невязка «,subst(xrez,x,f))$ Решение 0.56714329040978 Невязка 1. Особенности программирования для Maxima, использованные в этом примере, аналогичны приведённым выше в примере, касающемся метода половинного деления.

8.1.5 Метод хорд Метод основан на замене функции f (x) на каждом шаге поиска хордой, пересечение которой с осью X дает приближение корня.

При этом в процессе поиска семейство хорд может строится:

а) при фиксированном левом конце хорд, т.е. z = a, тогда начальная точка x0 = b;

8.2. Численное интегрирование б) при фиксированном правом конце хорд, т.е. z = b, тогда начальная точка x0 = a.

В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:

Процесс поиска продолжается до тех пор, пока не выполнится условие Метод обеспечивает быструю сходимость, если f (z) · f ”(z) 0, т.е.

хорды фиксируются в том конце интервала [a, b], где знаки функции f (z) и ее кривизны f ”(z) совпадают.

8.2 Численное интегрирование Задача численного интегрирования состоит в замене исходной подинтегральной функции f (x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией (x). Такой функцией обычно является полином (кусочный Таким образом где R = r(x)dx априорная погрешность метода на интервале инa тегрирования, а r(x) априорная погрешность метода на отдельном шаге интегрирования.

8.2.1 Обзор методов интегрирования Методы вычисления однократных интегралов называются квадратурными (для кратных интегралов кубатурными), и делятся на следующие группы:

• Методы Ньютона-Котеса. Здесь (x) полином различных степеней. Сюда относятся метод прямоугольников, трапеций, Симпсона.

• Методы статистических испытаний (методы Монте-Карло).

Здесь узлы сетки для квадратурного или кубатурного интегрирования выбираются с помощью датчика случайных чисел, ответ носит вероятностный характер. В основном применяются для вычисления кратных интегралов.

• Сплайновые методы. Здесь (x) кусочный полином с условиями связи между отдельными полиномами посредством системы коэффициентов.

• Методы наивысшей алгебраической точности. Обеспечивают оптимальную расстановку узлов сетки интегрирования и выбор веb 8.2.2 Метод прямоугольников Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени отрезком, параллельным оси абсцисс.

Формулы метода прямоугольников можно получить из анализа разложения функции f (x) в ряд Тейлора вблизи некоторой точки x = xi :

Рассмотрим диапазон интегрирования от xi до xi + h, где h шаг интегрирования. Вычислим интеграл от исследуемой функции 8.2. Численное интегрирование на этом промежутке:

таким образом, на базе анализа ряда Тейлора получена формула правых (или левых) прямоугольников и априорная оценка погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма степень при величине шага в формуле априорной оценки погрешности. В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид ·h f (xi ) = f (x)dx. Полученная оценка справедлива при наa личии непрерывной производной подинтегральной функции f (x).

8.2.3 Метод средних прямоугольников Здесь на каждом интервале значение функции считается в средней Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:

Пример функции Maxima, реализующей метод средних прямоугольников, представлен ниже:

(%i1) intpr(f,n,a,b):=block([h,i,s,_x],h:(b-a)/n, _x:a+h/2, s:0, for i:1 thru n do (s:s+float(subst(_x,x,f)),_x:_x+h),s:s*h)$ (%i2) intpr(x^2,100,-1,1);

(%o2) 0. 8.2.4 Метод трапеций Аппроксимация в этом методе осуществляется полиномом первой степени. На единичном интервале В случае равномерной сетки (h = const) Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников. Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удаётся далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.

Пример реализации метода трапеций в виде функции приведен ниже:

(%o1) x (%i2) inttrap(f,n,a,b):=block([h,i,s],h:(b-a)/n, s:(float(subst(a,x,f))+float(subst(b,x,f)))/2, for i:1 thru n-1 do (s:s+float(subst(a+i*h,x,f))), s:s*h)$ (%i3) inttrap(f,100,-1,1);

8.2. Численное интегрирование (%o3) 0. Подинтегральная функция задаётся в виде выражения Maxima.

Выражение, определяющее подинтегральную функцию, можно задавать и непосредственно при обращении к методу, как в следующем примере:

(%o4) 0. 8.2.5 Метод Симпсона При использовании данного метода подинтегральная функция f (x) заменяется интерполяционным полиномом второй степени P (x) параболой, проходящей через три соседних узла. Рассмотрим два шага интегрирования (h = const = xi+1 xi ), то есть три узла x0, x1, x2, через которые проведем параболу, воспользовавшись уравнением Ньютона:

Воспользовавшись полученным соотношением, вычислим интеграл по данному интервалу:

Для равномерной сетки и чётного числа шагов n формула Симпсона принимает вид:

рывности четвёртой производной подинтегральной функции.

Реализация метода Симпсона средствами Maxima представлена в следующем примере:

(%i1) intsimp(f,n,a,b):=block([h,h2,i,_x,s],h:(b-a)/n, h2:h/2, s:(float(subst(a,x,f))+float(subst(b,x,f)))/2+ for i:1 thru n-1 do (_x:_x+h, s:s+2*float(subst(_x+h2,x,f))+float(subst(_x,x,f))), (%i2) intsimp(x^2,100,-1,1);

(%o2) 0. 8.3 Методы решения систем линейных уравнений 8.3.1 Общая характеристика и классификация методов Рассмотрим систему линейных алгебраических уравнений (сокращенно СЛАУ):

f = (f1, f2. fm )T заданный вектор. Будем предполагать, что определитель матрицы A отличен от нуля, т.е. решение системы (8.1) существует.

Методы численного решения системы (8.1) делятся на две группы:

прямые методы ( точные ) и итерационные методы.

8.3. Методы решения систем линейных уравнений Прямыми методами называются методы, позволяющие получить решение системы (8.1) за конечное число арифметических операций.

К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.

Итерационные методы (методы последовательных приближений) состоят в том, что решение системы (8.1) находится как предел последовательных приближений x(n) при n, где n номер итерации.

При использовании методов итерации обычно задается некоторое малое число и вычисления проводятся до тех пор, пока не будет выполнена оценка x(n) x. К этим методам относятся метод Зейделя, Якоби, метод верхних релаксаций и т.д.

Следует заметить, что реализация прямых методов на компьютере приводит к решению с погрешностью, т.к. все арифметические операции над переменными с плавающей точкой выполняются с округлением. В зависимости от свойств матрицы исходной системы эти погрешности могут достигать значительных величин.

8.3.2 Метод Гаусса Запишем систему (8.1), в развернутом виде

Метод Гаусса состоит в последовательном исключении неизвестных из этой системы. Предположим, что a11 = 0. Последовательно умножая первое уравнение на и складывая с i-м уравнением, исключим x1 из всех уравнений кроме первого. Получим систему

330 Глава 8. Реализация некоторых численных методов где Аналогичным образом из полученной системы исключим x2. Последовательно, исключая все неизвестные, получим систему треугольного вида

Описанная процедура называется прямым ходом метода Гаусса. Заl) метим, что ее выполнение было возможно при условии, что все ai,i, l = 1, 2. m1 не равны нулю. Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.

Эта процедура получила название обратный ход метода Гаусса.

Метод Гаусса может быть легко реализован на компьютере. При выполнении вычислений, как правило, промежуточные значения матрицы A не представляют интереса. Поэтому численная реализация метода сводится к преобразованию элементов массива размерности m (m + 1), где m + 1-й столбец содержит элементы правой части системы.

Для контроля ошибки реализации метода используются, так называемые, контрольные суммы. Схема контроля основывается на следующем очевидном положении. Увеличение значения всех неизвестных на единицу равносильно замене данной системы контрольной системой, в которой свободные члены равны суммам всех коэффициентов соответствующей строки. Создадим дополнительный столбец, хранящий сумму элементов матрицы по строкам. На каждом шаге реализации прямого хода метода Гаусса будем выполнять преобразования и 8.3. Методы решения систем линейных уравнений над элементами этого столбца, и сравнивать их значение с суммой по строке преобразованной матрицы. В случае не совпадения значений счет прерывается.

Один из основных недостатков метода Гаусса связан с тем, что при его реализации накапливается вычислительная погрешность.

Для систем порядка m число действий умножения и деления близm ко к и быстро растет с величиной m.

Для того, чтобы уменьшить рост вычислительной погрешности применяются различные модификации метода Гаусса. Например, метод Гаусса с выбором главного элемента по столбцам, в этом случае на каждом этапе прямого хода строки матрицы переставляются таким образом, чтобы диагональный угловой элемент был максимальным.

При исключении соответствующего неизвестного из других строк деление будет производиться на наибольший из возможных коэффициентов и, следовательно, относительная погрешность будет наименьшей.

Пример реализации метода Гаусса в Maxima приведен в функции ниже (применен метод без выбора главного элемента):

(%i1) gauss(a0,b0,n):=block([a,b,i,j,k,d], a:copymatrix (a0), b:copymatrix(b0), x:copymatrix(b0), for j:i+1 thru n do (a[k,j]:a[k,j]-a[i,j]*d), b[i,1]:b[i,1]-a[i,j]*x[j,1]), x[i,1]:b[i,1]/a[i,i] Пример обращения к функции, реализующей метод Гаусса:

(%o2) 1 3 1 (%o3) 6 (%o4) Проверка вычислений показывает, что перемножение матрицы A на вектор решения zz дает вектор, совпадающий с вектором правых частей bb.

(%o5) 6. Существует метод Гаусса с выбором главного элемента по всей матрице. В этом случае переставляются не только строки, но и столбцы. Использование модификаций метода Гаусса приводит к усложнению алгоритма увеличению числа операций и соответственно к росту времени счета.

Выполняемые в методе Гаусса преобразования прямого хода, приведшие матрицу A системы к треугольному виду позволяют вычислить определитель матрицы Метод Гаусса позволяет найти и обратную матрицу. Для этого необходимо решить матричное уравнение где E – единичная матрица. Его решение сводится к решению m систем у вектора (j) j–я компонента равна единице, а остальные компоненты равны нулю.

8.3. Методы решения систем линейных уравнений 8.3.3 Метод квадратного корня Метод квадратного корня основан на разложении матрицы A в произведение где S верхняя треугольная матрица с положительными элементами на главной диагонали, S T транспонированная к ней матрица.

Пусть A матрица размером m m. Тогда Из условия (8.2) получаются уравнения Так как матрица A симметричная, не ограничивая общности, можно считать, что в системе (8.3) выполняется неравенство i j. Тогда (8.3) можно переписать в виде В частности, при i = j получится Далее, при i j получим 334 Глава 8. Реализация некоторых численных методов По приведённым формулам находятся рекуррентно все ненулевые элементы матрицы S.

Обратный ход метода квадратного корня состоит в последовательном решении двух систем уравнений с треугольными матрицами.

Решения этих систем находятся по рекуррентным формулам:

Всего метод квадратного корня при факторизации A = S T S треm бует примерно операций умножения и деления и m операций извлечения квадратного корня.

Пример функции, реализующей метод квадратного корня:

(%i1) holetsk(a0,b0):=block([L,Lt,x,y,i,j,k,n], n:length(a0), L:zeromatrix(n,n), for k:1 thru j-1 do (s:s+L[i,k]*L[j,k]), L[i,j]:1/L[j,j]*(a0[i,j]-s) for k:1 thru i-1 do (s:s+L[i,k]^2), L[i,i]:sqrt(a0[i,i]-s) ),Lt:transpose(L), y:zeromatrix(n,1), x:zeromatrix(n,1), 8.3. Методы решения систем линейных уравнений for k:1 thru i-1 do (s:s+L[i,k]*y[k,1]), y[i,1]:(b0[i,1]-s)/L[i,i] for k:n thru i+1 step -1 do (s:s+Lt[i,k]*x[k,1]), x[i,1]:(y[i,1]-s)/Lt[i,i] Тест данной функции (решение системы Ax = B, B матрица n1, A квадратная симметричная матрица nn, результат решения вектор n 1):

(%i2) A:matrix([4,1,1],[1,4,1],[1,1,4])$ B:matrix([1],[1],[1])$ Результаты вычислений:

(%o5) 8.3.4 Корректность постановки задачи и понятие При использовании численных методов для решения тех или иных математических задач необходимо различать свойства самой задачи и свойства вычислительного алгоритма, предназначенного для ее решения.

Говорят, что задача поставлена корректно, если решение существует и единственно и если оно непрерывно зависит от входных данных.

Последнее свойство называется также устойчивостью относительно входных данных.

Корректность исходной математической задачи еще не гарантирует хороших свойств численного метода ее решений и требует специального исследования.

Известно, что решение задачи (8.1) существует тогда и только тогда, когда det A = 0. В этом случае можно определить обратную матрицу A1 и решение записать в виде x = A1 f.

Исследование устойчивость задачи (8.1) сводится к исследованию зависимости ее решения от правых частей f и элементов aij матрицы A. Для того чтобы можно было говорить о непрерывной зависимости вектора решений от некоторых параметров, необходимо на множестве m-мерных векторов принадлежащих линейному пространству H, ввести метрику.

В линейной алгебре предлагается определение множества метрик lp норма x часто используемые метрики соответственно записываются в следующем виде:

8.3. Методы решения систем линейных уравнений Обычно рассматривают два вида устойчивости решения системы (8.1):

• по правым частям;

• по коэффициентам системы (8.1) и по правым частям.

Наряду с исходной системой (8.1) рассмотрим систему с возмущенными правыми частями где f = f + f возмущенная правая часть системы, а x = x + x возмущенное решение.

Можно получить оценку, выражающую зависимость относительной погрешности решения от относительной погрешности правых частей где MA = A · A1 число обусловленности матрицы A (в современной литературе это число обозначают как cond(A)). Если число обусловленности велико (MA 10k, k 2), то говорят, что матрица A плохо обусловлена. В этом случае малые возмущения правых частей системы (8.1), вызванные либо неточностью задания исходных данных, либо вызванные погрешностями вычисления существенно влияют на решение системы.

Если возмущение внесено в матрицу A, то для относительных возмущений решения имеет место следующая оценка:

В Maxima матричные нормы вычисляются посредством функции mat_norm. Синтаксис вызова: mat_norm(M, type), где M матрица, type тип нормы, type может быть равен 1 (норма A 1 ), inf (норма A ), f robenius (норма A 2 ).

Пример вычисления указанных видов нормы в Maxima:

338 Глава 8. Реализация некоторых численных методов (%i2) mat_norm(A,1);

(%o2) (%i3) mat_norm(A,inf);

(%o3) (%i4) mat_norm(A,frobenius);

(%o4) Вычислим число обусловленности для плохо и хорошо обусловленных матриц:

(%o2) 1. (%i3) A1:invert(A);

99.99999999999992 99. 98.99999999999992 99. (%i4) nrA1:mat_norm(A1,frobenius);

(%o4) 199. (%i5) MA:nrA*nrA1;

(%o5) 398. Таким образом, для плохо обусловленной матрицы число обусловленности достигает почти 400.

Аналогичным путём (с использованием нормы Фробениуса) для матрицы B = число обусловленности составило M B = 2.

8.4. Итерационные методы 8.3.5 О вычислительных затратах Один из важных факторов предопределяющих выбор того или иного метода при решении конкретных задач, является вычислительная эффективность метода. Учитывая, что операция сложения выполняется намного быстрее, чем операция умножения и деления, обычно ограничиваются подсчетом последних. Для решения СЛАУ методом Гаусса без выбора главного элемента требуется умножений и делений, решение СЛАУ методом квадратного корня требует + + и m операций извлечения корней. При больших значениях размерности m, можно сказать, что вычислительные 8.4 Итерационные методы В приближенных или итерационных методах решение системы линейных алгебраических уравнений является пределом итерационной последовательности, получаемой с помощью этих методов. К ним относятся: метод простой итерации, метод Зейделя и др. Итерационные методы выгодны для системы специального вида, со слабо заполненной матрицей очень большого вида порядка 103. 105.

Для итерационных методов характерно то, что они требуют начальных приближений значений неизвестных, решение ищется в виде последовательности, постепенно улучшающихся приближений, и кроме того, итерационный процесс должен быть сходящимся. В вычислительной практике процесс итерации обычно продолжается до тех пор, пока два последовательных приближения не совпадут в пределах заданной точности.

8.4.1 Матричная формулировка итерационных методов решения систем линейных уравнений При использовании СКМ Maxima вполне обосновано использование и матричной формулировки итерационных методов.

Рассмотрим решение системы Ax = f (A квадратная матрица, f вектор правых частей, x вектор неизвестных). Обозначим 340 Глава 8. Реализация некоторых численных методов A = L + D + U, где L нижняя треугольная матрица с нулевыми диагональными элементами; D диагональная матрица; U верхняя треугольная матрица с нулевыми диагональными элементами.

Для решения этой системы рассмотрим итерационный процесс где det(Hi ) = 0, или где Pi = I Pi A оператор i-го шага итерационного процесса;

Итерационный процесс сходящийся, если последовательность сходится к решению x при любом x0.

Если матрица не зависит от номера итерации, итерационный процесс называется стационарным:

Необходимым и достаточным условием сходимости стационарного процесса является выполнение условия (P ) 1, где (P ) спектральный радиус матрицы P (наибольшее по модулю собственное число матрицы P ).

С использованием введённых обозначений метод простой итерации (метод Якоби) даётся формулой:

а метод Гаусса–Зейделя формулой:

Рассмотрим поэлементные расчетные соотношения для методов Якоби и Гаусса Зейделя.

Все элементы главной диагонали матрицы I = D1 A равны нулю, остальные элементы равны, i, j = 1, n. Свободный член уравнеaii ния (8.4) равен.

8.4. Итерационные методы вается в виде xk+1 = Cxk + E, где Cij = ; k = 0, 1. i, j = 1, n;

Для метода Гаусса–Зейделя xk+1 = (D + L)1 U xk + (D + L)1 f, или (D + L)xk+1 = U xk + b, xk+1 = Bxk+1 + Exk + e, где Рассмотрим решение конкретной системы уравнений Ax = b методом Якоби:

Вычисляем элементы матрицы B и вектора e:

Вычислим значения x по формуле xk+1 = Bxk + e. Для решения использована следующая последовательность команд Maxima:

преобразование заданных матриц (%i1) A:matrix([8,-1,2],[1,9,3],[2,-3,10])$ b:matrix([8],[18],[5])$ A0:matrix([A[1,1],A[1,1],A[1,1]], B:-A/A0+diagmatrix(3,1)$ e:b/matrix([A[1,1]],[A[2,2]],[A[3,3]])$ x:e$ 342 Глава 8. Реализация некоторых численных методов собственно вычисление решения (%i7) xt:float(B.x+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ xt:float(B.xt+e)$ float(r); /* оценка сходимости*/ float(A.x1-b); /* оценка невязки*/ 1. (%o18) 1.3018148195786949 6. 2. (%o19) 1.738702477211973 3. 8.4.2 Метод простой итерации Для решения системы линейных алгебраических уравнений (8.1) итерационным методом её необходимо привести к нормальному виду:

Стационарное итерационное правило получаем, если матрица B и вектор g не зависят от номера итерации: xk+1 = P xk + g. Нестационарное итерационное правило получаем если матрица B или вектор g изменяются с ростом номера итерации: xk+1 = Pk xk + g k.

Стационарное итерационное правило обычно называют методом простой итерации. Предел итерационной последовательности является точным решением системы (8.5) или (8.1).

Для того, чтобы метод простой итерации сходился при любом начальном приближении, необходимо и достаточно, чтобы все собственные значения матрицы В были по модулю меньше единицы.

8.4. Итерационные методы В силу того, что проверить сформулированное выше условие достаточно сложно на практике применяют следующие достаточные признаки:

• для того чтобы метод простой итерации сходился, достаточно, чтобы какая-либо норма матрицы P была меньше единицы;

• для того чтобы метод простой итерации сходился, достаточно, чтобы выполнялось одно из следующих условий:

Для определения скорости сходимости можно воспользоваться следующей теоремой: если какая-либо норма матрицы P, согласованная с данной нормой вектора, меньше единицы, то имеет место следующая оценка погрешности метода простой итерации:

где x точное решение системы (8.1).

Другими словами, условие сходимости выполняется, если выполняется условие доминирования диагональных элементов матрицы исn i,j= В этом случае легко можно перейти от системы вида (8.1) к системе (8.5). Для этого разделим i–ое уравнение системы на ai,i и выразим 344 Глава 8. Реализация некоторых численных методов т.е. для матрицы P будет выполнено одно из условий сходимости, где Пример реализации метода простой итерации средствами Maxima с печатью промежуточных результатов представлен в скрипте ниже:

(%i1) iterpr(a0,b0,x,n,eps):=block([a,b,x0,i,j,s,sum,p], a:copymatrix (a0), b:copymatrix(b0), x0:copymatrix(x), sum:0, p:p+1, print(«p= «,p,» x= «,float(x)), for j:1 thru n do (s:s-a[i,j]*x0[j,1]), s:s/a[i,i], x[i,1]:x0[i,1]+s, sum:sum+abs(s) x0:copymatrix(x) float(x))$ 8.4.3 Метод Зейделя В методе Зейделя система (8.1) также приводится к системе (8.5).

Но при вычислении последующей компоненты вектора используются уже вычисленные компоненты этого вектора.

Итерационная формула метода в скалярной форме записывается следующим образом:

Установим связь между методом Зейделя и методом простой итерации. Для этого матрицу B представим в виде суммы двух матриц:

8.4. Итерационные методы Итерационная формула метода Зейделя в матричной форме записывается в виде:

т.е. метод Зейделя эквивалентен методу простой итерации с матрицей Исходя из полученной аналогии методов Зейделя и простой итерации, можно сформулировать следующий признак сходимости метода Зейделя: для того чтобы метод Зейделя сходился, необходимо и достаточно, чтобы все собственные значения матрицы (E H) F по модулю были меньше единицы.

Другими словами, чтобы метод Зейделя сходился, необходимо и достаточно, чтобы все корни уравнения по модулю были меньше единицы, т.к.

Сформулируем достаточный признак сходимости: для того, чтобы метод Зейделя сходился, достаточно, чтобы выполнилось одно из условий:

При использовании метода Зейделя итерационный процесс сходится к единственному решению быстрее метода простых итераций.

Пример реализации метода Зейделя:

(%i1) seidel(a0,b0,x,n,eps):=block([a,b,i,j,s,sum,p], a:copymatrix (a0), b:copymatrix(b0), sum:0, p:p+1, print(«p= «,p), for j:1 thru n do (s:s-a[i,j]*x[j,1]), s:s/a[i,i], x[i,1]:x[i,1]+s, sum:sum+abs(s) float(x))$ Пример решения простой системы методом Зейделя:

p=1p=2 p=3p=4p=5p= 1. (%o5) 0. 2. 8.5. Решение обыкновенных дифференциальных уравнений 8.5 Решение обыкновенных дифференциальных 8.5.1 Методы решения задачи Коши Среди задач, с которыми приходится иметь дело в вычислительной практике, значительную часть составляют различные задачи, сводящиеся к решению обыкновенных дифференциальных уравнений.

Обычно приходится прибегать к помощи приближенных методов решения подобных задач. В случае обыкновенных дифференциальных уравнений в зависимости от того, ставятся ли дополнительные условия в одной или нескольких точках отрезка изменения независимой переменной, задачи обычно подразделяются на одноточечные (задачи с начальными условиями или задачи Коши) и многоточечные. Среди многоточечных задач наиболее часто в прикладных вопросах встречаются так называемые граничные задачи, когда дополнительные условия ставятся на концах рассматриваемого отрезка.

В дальнейшем ограничимся рассмотрением численных методов решения задачи Коши. Для простоты изложения методов решения задачи будем рассматривать случай одного обыкновенного дифференциального уравнения первого порядка.

Пусть на отрезке x0 x L требуется найти решение y(x) дифференциального уравнения удовлетворяющее при x = x0 начальному условию y(x0 ) = y0.

Будем считать, что условия существования и единственности решения поставленной задачи Коши выполнены.

На практике найти общее либо частное решение задачи Коши удается для весьма ограниченного круга задач, поэтому приходится решать эту задачу приближенно.

Отрезок [x0, L] накрывается сеткой (разбивается на интервалы) чаще всего с постоянным шагом h (h = xn+1 xn ), и по какомуто решающему правилу находится значение yn+1 = y(xn+1 ). Таким образом, результатом решения задачи Коши численными методами является таблица, состоящую из двух векторов: x = (x0, x1. xn ) вектора аргументов и соответствующего ему вектора значений искомой функции y = (y0, y1. yn ).

Численные методы (правила), в которых для нахождения значения функции в новой точке используется информация только об одной (предыдущей) точке, называются одношаговыми.

Численные методы (правила), в которых для нахождения значения функции в новой точке используется информация о нескольких (предыдущих) точках, называются многошаговыми.

Из общего курса обыкновенных дифференциальных уравнений широкое распространение получил аналитический метод, основанный на идее разложения в ряд решения рассматриваемой задачи Коши.

Особенно часто для этих целей используется ряд Тейлора. В этом случае вычислительные правила строятся особенно просто.

Приближенное решение ym (x) исходной задачи ищут в виде Здесь y (0) (x0 ) = y(x0 ), y (1) (x0 ) = y (x0 ) = f (x0, y0 ), а значения y (x0 ), i = 2, 3. m находят по формулам, полученным последовательным дифференцированием заданного уравнения:

Для значений x, близких к x0, метод рядов (8.7) при достаточно большом значении m дает обычно хорошее приближение к точному решению y(x) задачи (8.6). Однако с ростом расстояния |x x0 | погрешность приближения искомой функции рядом возрастает по абсолютной величине (при одном и том же количестве членов ряда), и правило (8.7) становится вовсе неприемлемым, когда x выходит из области сходимости соответствующего ряда (8.7) Тейлора.

Если в выражении (8.7) ограничиться m = 1, то для вычисления новых значений y(x) нет необходимости пересчитывать значение производной, правда и точность решения будет невысока.

При использовании системы компьютерной алгебры более естественным выглядит метод последовательных приближений Пикара.

8.5. Решение обыкновенных дифференциальных уравнений Рассмотрим интегрирование единичного дифференциального уравdy нения = f (x, y) на отрезке [x0, x] с начальным условием y(x0 ) = y0.

При формальном интегрировании получим:

Процедура последовательных приближений метода Пикара реализуется согласно следующей схеме В качестве примера рассмотрим решение уравнения y = y, при y(0) = 1, x0 = 0:

(%i1) rp:-y$ y0:1$ x0:0$ /*rp-правая часть уравнения */ (%i4) y1:y0+integrate(subst(y0,y,rp),x,x0,x);

/* y1 — первое приближение */ (%o4) 1 x (%i5) y2:y0+integrate(subst(y1,y,rp),x,x0,x);

/* y2 — второе приближение */ (%i6) y3:y0+integrate(subst(y2,y,rp),x,x0,x);

(%i7) expand(%); /* Очевидное решение рассматриваемого ОДУ экспонента y=exp(-x).

350 Глава 8. Реализация некоторых численных методов 8.5.2 Метод рядов, не требующий вычисления производных правой части уравнения Естественно поставить задачу о таком усовершенствовании приведенного выше одношагового метода, которое сохраняло бы основные его достоинства, но не было бы связано с нахождением значений производных правой части уравнения где xn+1 = xn + h.

Чтобы выполнить это условие (последнее), производные y (i) (x), i = 2, 3. m, входящие в правую часть уравнения (8.9), можно заменить по формулам численного дифференцирования их приближенными выражениями через значение функции y и учесть, что y (x) = f [x, y(x)].

8.5.2.1 Метод Эйлера В случае m = 1 приближенное равенство (8.9) не требует вычисления производных правой части уравнения и позволяет с погрешностью порядка h2 находить значение y(xn + h) решения этого уравнения по известному его значению y(xn ). Соответствующее одношаговое правило можно записать в виде Это правило (8.10) впервые было построено Эйлером и носит его имя. Иногда его называют также правилом ломаных или методом касательных. Метод Эйлера имеет относительно низкий порядок точh2 на одном шаге. Практическая оценка погрешности приности ближенного решения может быть получена по правилу Рунге.

Пример реализации метода Эйлера средствами Maxima приведён в следующем примере:

(%i1) euler1(rp,fun,y0,x0,xend,h):=block([OK,_x,_y,_y1,rez], _x:x0, _y:y0, rez:[_y], OK:-1, eps:0.1e-7, if ((_x+hxend) or (abs(_x+h-xend)eps)) 8.5. Решение обыкновенных дифференциальных уравнений _y1:makelist(float(_y[i]+h*subst([fun[i]=_y[i],x=_x], rp[i])),i,1,length(_y)),rez:append(rez,[_y1]), Правые части решаемых дифференциальных уравнений передаются в функцию euler1 в списке rp. По умолчанию предполагается, что список имён зависимых переменных f un, имя независимой переменной x. Начальные значения независимой и зависимых переменных список y0 и скалярная величина x0, граница интервала интегрирования величина xend, шаг интегрирования h.

Следующий пример обращение к функции euler1. Приведено решение системы из трёх дифференциальных уравнений на интервале [0, 1] с шагом h = 0.1:

С начальными условиями y(0) = 1.0; v(0) = 1.0; z(0) = 0, решением уравнений данной системы будут функции:

(%o2) [[1, 1, 0], [0.8, 0.5, 0.03], [0.64, 0.25, 0.09], [0.512, 0.125, 0.18], [0.4096, 0.0625, 0.3], [0.32768, 0.03125, 0.45], [0.262144, 0.015625, 0.63], [0.2097152, 0.0078125, 0.84], [0.16777216, 0.00390625, 1.08], [0.134217728, 0.001953125, 1.35], [0.1073741824, 9.7656249999999913 10 4, 1.65]] Проверить решение можно сравнивая графики точного решения и множества вычисленных приближенных значений. Пример последовательности команд, позволяющих выделить отдельные компоненты 352 Глава 8. Реализация некоторых численных методов решения системы ОДУ и построить график точного и приближенного решения третьего уравнения системы, представлен ниже (точные решения списки yf, vf, zf ; приближенные решения списки yr, vr, zr; список значений независимой переменной xg).

(%i3) rez:euler1([-2*y,-5*v,3*x],[y,v,z],[1,1,0],0,1.0,0.1)$ n:length(rez)$ yr:makelist(rez[k][1], k, 1, n)$ vr:makelist(rez[k][2], k, 1, n)$ zr:makelist(rez[k][3], k, 1, n)$ xg:makelist(0.1*(k-1),k,1,n)$ yf:makelist(exp(-2*xg[k]), k, 1, n)$ vf:makelist(exp(-5*xg[k]), k, 1, n)$ zf:makelist(3*xg[k]^2/2, k, 1, n)$ plot2d ([[discrete, xg,zr],[discrete, xg,zf]], Уменьшение шага h приводит к уменьшению погрешности решения (в данном примере шаг 0.1).

8.5.2.2 Метод Рунге-Кутта Изложим идею метода на примере задачи Коши:

Интегрируя это уравнение в пределах от x до x + h (0 h 1), получим равенство которое посредством последнего интеграла связывает значения решения рассматриваемого уравнения в двух точках, удаленных друг от друга на расстояние шага h.

Для удобства записи выражения (8.11) используем обозначение y = y(x + h) y(x) и замену переменной интегрирования t = x + h.

8.5. Решение обыкновенных дифференциальных уравнений Окончательно получим:

В зависимости от способа вычисления интеграла в выражении (8.12) получают различные методы численного интегрирования обыкновенных дифференциальных уравнений.

Рассмотрим линейную комбинацию величин i, i = 0, 1. q, которая будет являться аналогом квадратурной суммы и позволит вычислить приближенное значение приращения y:

где Метод четвертого порядка для q = 3, являющийся аналогом широко известной в литературе четырехточечной квадратурной формулы трех восьмых, имеет вид где Особо широко известно другое вычислительное правило типа Рунге-Кутта четвертого порядка точности:

354 Глава 8. Реализация некоторых численных методов где Метод Рунге-Кутта имеет погрешность четвертого порядка ( h4 ).

Функция Maxima, реализующая метод Рунге-Кутта 4-го порядка, приведена в следующем примере (с печатью промежуточных результатов):

(%i1) rk4(rp,fun,y0,x0,xend,h):=block( [OK,n,h1,_x,_y,_k1,_k2,_k3,_k4,rez], _x:x0, _y:y0, rez:[_y], OK:-1, h1:h, n:length(_y), if (_x+h1=xend) then (h1:xend-_x, OK:1), _k1:makelist(float(h1*subst([fun[i]= float(_y[i]),x=float(_x)],rp[i])),i,1,n), _k2:makelist(float(h1*subst([fun[i]= float(_y[i]+_k1[i]/2),x=float(_x+h1/2)], _k3:makelist(float(h1*subst([fun[i]= float(_y[i]+_k2[i]/2),x=float(_x+h1/2)], _k4:makelist(float(h1*subst([fun[i]= float(_y[i]+_k3[i]),x=float(_x+h1)],rp[i])), _y1:makelist(float(_y[i]+ (_k1[i]+2*_k2[i]+2*_k3[i]+_k4[i])/6),i,1,n), Пример обращения к функции rk4 представлен следующей последовательностью команд (решалась та же система, что и при тестировании метода Эйлера):

8.5. Решение обыкновенных дифференциальных уравнений x= 0.1 y= [0.81873333333333,0.60677083333333,1.015] x= 0.2 y= [0.67032427111111,0.36817084418403,1.06] x= 0.3 y= [0.54881682490104,0.22339532993458,1.135] x= 0.4 y= [0.44933462844064,0.13554977050718,1.24] x= 0.5 y= [0.3678852381253,0.082247647208783,1.375] x= 0.6 y= [0.30119990729446,0.04990547343658,1.54] x= 0.7 y= [0.24660240409888,0.030281185705008,1.735] x= 0.8 y= [0.20190160831589,0.018373740284549,1.96] x= 0.9 y= [0.16530357678183,0.011148649703906,2.215] x= 1.0 y= [0.13533954843051,0.0067646754713805,2.5] Приложения Таблица 1: Сокращённый список основных функций Maxima Функция или Краткое описание переменная ’, ’’,, % простейшие команды, см. стр. addcol Функция добавляет столбец к матрице, см.

addrow Функция добавляет строку к матрице, см.

algsys Функция решает полиномиальные системы уравнений. Допускаются системы из одного уравнения с одной неизвестной. Кроме того, допускаются недоопределенные системы, см. стр. 88– allroots Функция, которая находит и печатает все (в том числе и комплексные) корни полиномиального уравнения с действительными antidi Функция выполняет интегрирование выражений с произвольными функциями, перед 8.5. Решение обыкновенных дифференциальных уравнений Функция или Краткое описание переменная append Функция позволяет склеивать два списка, arrayinfo Функция печатает информацию о массиве его вид, число индексов, размер, см.

arrays Переменная содержит список имен массивов первого и второго видов, определенных array Функция определяет массив с данным именем, определенным количеством индексов и assume Функция вводит информацию о переменной atvalue Функция позволяет задать значение функции и ее производных при некоторых значениях аргументов, см. стр. augmented_lagran- Функция осуществляет минимизацию ФНП gian_method с ограничениями, см. стр. либо до конца файла, либо до синтаксической ошибки, либо до некорректной операции, см. стр. Функция или Краткое описание переменная bс2 Функция позволяет учесть краевые условия cabs Функция возвращает модуль комплексного carg Функция возвращает фазу комплексного cfdisrep Функция преобразует список (как правило результат выполнения функции cf) в собственно цепную дробь, см. стр. cf Функция Создает цепную дробь, аппроксимирующую данное выражение. Выражение должно состоять из целых чисел, квадратных корней целых чисел и знаков арифметических операций. Возвращаемый результат список, см. стр. cfdirep Функция преобразует список в собственно changevar реализует замену переменных в интеграле, charpoly Функция является до некоторой степени избыточной она вычисляет характеристический полином матрицы (корни этого полинома собственные значения матрицы), closele Функция прекращает вывод в файл, см.

COl Функция выделяет заданный столбец матрицы, см. стр. 43– 8.5. Решение обыкновенных дифференциальных уравнений Функция или Краткое описание переменная combine Функция объединяет слагаемые с идентичным знаменателем, см. стр. 50– compile Функция сначала транслирует функцию Maxima на язык LISP, а затем компилирует эту функцию LISP’a до двоичных кодов conjugate Функция для вычисления комплексносопряжённых выражений, см. стр. 80– cons Функция позволяет добавлять элемент в contrib_ode Функция решает дифференциальные уравнения (больше возможностей, чем у ode2), copylist Функция создаёт копию списка, см. стр. create_list Функция создаёт список, см. стр. copymatrix Функция Создаёт копию матрицы, см.

cspline Функция строит сплайн-интерполяцию, см.

dene Функция позволяет преобразовать выражение в функцию, см. стр. demoivre Функция заменяет все экспоненты с мнимыми показателями на соответствующие тригонометрические функции, см. стр. 80– denom Функция выделяет знаменатель, см. стр. depends Функция позволяет декларировать, что переменная зависит от одной или нескольких Функция или Краткое описание переменная desolve Функция решает дифференциальные уравнения и системы дифференциальных уравнений методом преобразования Лапласа, determinant Функция вычисляет детерминант матрицы, di Функция выполняет дифференцирование, display2d Переменная включает или выключает display Функция печатает значения своих аргументов вместе с их именем, каждое в отдельной disp Функция печатает значения своих аргументов, причем каждое значение печатается в divide Функция позволяет вычислить частное и draw2d строит двумерные графики, см. стр. 248– draw3d строит трёхмерные графики, см. стр. 248– echelon Функция преобразует матрицу к верхней eigenvalues Функция аналитически вычисляет собственные значения матрицы, см. стр. 83– 8.5. Решение обыкновенных дифференциальных уравнений Функция или Краткое описание переменная eigenvectors Функция аналитически вычисляет собственные значения и собственные вектора eliminate Функция исключает из системы уравнений указанные переменные. Оставшиеся уравнения приводятся к виду с нулевой правой endcons Функция позволяет добавлять элемент в конец списка, см. стр. ev Функция является основной функцией, обрабатывающей выражения, см. стр. 50– expand Функция раскрывает скобки, см. стр. 50– exponentialize Функция приводит комплексное выражение express Функция преобразует дифференциальные factor Функция представляет в виде произведения некоторых сомножителей заданное выражение, см. стр. 50– factorsum Функция факторизует отдельные слагаемые в выражении, см. стр. 50– llarray Функция позволяет заполнять одноиндексные массивы третьего вида из списка, см.

nd_root Функция находит корень уравнения на заданном интервале методом деления отрезка rst Функция выделяет первый элемент списка, Функция или Краткое описание переменная oat Функция конвертирует любые числа в выражениях в числа машинной точности, см.

fourier Функция позволяет вычислить коэффициенты ряда Фурье, см. стр. foursimp Функция позволяет упростить коэффициенты ряда Фурье, см. стр. fullratsimp Функция вызывает функцию ratsimp до тех пор, пока выражение не перестанет меняться, 57– genmatrix Функция возвращает матрицу заданной gfactorsum Функция представляет в виде сомножителей слагаемые выражения с комплексными gfactor Функция представляет в виде сомножителей выражение с комплексными числами, gradef Функция определяет результат дифференцирования функции по своим аргументам, gramschmidt Функция вычисляет ортонормированную ic1 Функция позволяет учесть начальное условие в решениях дифференциальных уравнений первого порядка, см. стр. 8.5. Решение обыкновенных дифференциальных уравнений Функция или Краткое описание переменная ic2 Функция позволяет учесть начальные условия в решениях дифференциальных уравнений второго порядка, см. стр. ident Функция возвращает единичную матрицу ilt Функция реализует обратное преобразование Лапласа, см. стр. 144– imagpart Функция возвращает действительную integrate Функция выполняет интегрирование заданного выражения по указанной переменной (неопределенная константа не добавляется). Можно также указать пределы интегрирования в этом случае вычисляется invert функция выполняет обращение матрицы, join функция выполняет компоновку списков, lagrange Функция строит интерполяцию полиномом lambda создает лямбда-выражение (безымянную функцию). Лямбда-выражение может использоваться в некоторых случаях как Функция или Краткое описание переменная laplace Функция реализует прямое преобразование ldisplay Функция печатает значения своих аргументов вместе с их именем и метками %t, см.

ldisp Функция печатает значения своих аргументов вместе с метками %t, см. стр. length Функция возвращает длину списка, см.

lhs Функция выделяет левую часть уравнения, limit функция осуществляет вычисление пределов, см. стр. linearinterpol Функция строит линейную интерполяцию, linsolve Функция решает системы линейных и полиномиальных уравнений. Допускаются недоопределенные системы, см. стр. 88– listarray Функция печатает содержимое массивов load Функция загружает тот или иной файл:

load(somele); Тип загрузки зависит от типа файла (макрос Maxima, программа на 8.5. Решение обыкновенных дифференциальных уравнений Функция или Краткое описание переменная logcontract Функция компактифицирует логарифмы в make_array Функция создает массивы третьего вида, содержимое которых печатается автоматически, см. стр. makelist Функция позволяет создавать списки, см.

matrix Функция возвращает матрицу, заданную matrixmap Функция для заполнения матрицы значениями некоторой функции, см. стр. 43– mattrace Функция вычисляет след матрицы (сумму max перебирает свои аргументы и находит максимальное число, см. стр. member Функция возвращает true, если ее первый аргумент является элементом заданного списка, и f alse в противном случае, см.

min перебирает свои аргументы и находит минимальное число, см. стр. minor вычисляет миноры матрицы, см. стр. 83– mnewton Функция находит корень системы уравнений многомерным методом Ньютона. Для использования функции необходимо сначала загрузить пакет mnewton, см. стр. Функция или Краткое описание переменная multthru Функция умножает каждое слагаемое в сумме на множитель, причем при умножении скобки в выражении не раскрываются, newton Функция находит корень указанной функции методом Ньютона, см. стр. nroots Функция, которая возвращает количество уравнения с действительными коэффициентами, которые локализованы в указанном ode2 Функция решает дифференциальные уравнения первого и второго порядков, см.

odelin Функция решает однородные линейные pade Функция аппроксимирует отрезок ряда plog представляет основную ветвь комплексного plot2d, wxplot2d строит двумерные графики, см. стр. 67– plot3d, wxplot3d строит трёхмерные графики, см. стр. 67– 8.5. Решение обыкновенных дифференциальных уравнений Функция или Краткое описание переменная polarform Функция приводит комплексное выражение polyfactor Переменная определяет форму выдачи powerseries Функция строит разложение в степенной print печатает значения всех своих аргументов в product Функция реализует цикл умножения, см.

properties Функция печатает свойства переменной, см.

radcan Функция упрощает выражения со вложенными степенями и логарифмами, см.

ratepsilon Переменная задает точность преобразования действительного числа в рациональное, ratexpand Функция раскрывает скобки в выражении.

ratfac Переменная включает или выключает частичную факторизацию выражений при сведении их к CRE. Изначально установлено значение f alse, см. стр. 57– ratsimpexpons Переменная управляет упрощением показателей степени в выражениях, см. стр. 57– Функция или Краткое описание переменная ratsimp Функция приводит все куски (в том числе не является дробно-рациональной функцией, к каноническому представлению, производя упрощения, которые не делает функция rat. Повторный вызов функции может ratsubst Функция Реализует синтаксическую подстановку для рациональных выражений, ratvars Функция позволяет изменить алфавитный порядок главности переменных, принятый по умолчанию, см. стр. 57– rat Функция приводит выражение к каноническому представлению и снабжает его меткой /R/. Она упрощает любое выражение, рассматривая его как дробнорациональную функцию, т.е. работает с арифметическими операциями и с возведением в целую степень, см. стр. 57– realpart Функция возвращает действительную read основная функция для считывания вводимых пользователем выражений, см. стр. read_matrix, функция для ввода массивов чисел, см.

realroots Функция выдает действительные корни полиномиального уравнения с действительными коэффициентами, см. стр. 88– 8.5. Решение обыкновенных дифференциальных уравнений Функция или Краткое описание переменная rectform Функция Приводит комплексное выражение к алгебраической форме, см. стр. 80– remarray Функция уничтожает массив или массивы, remove Функция удаляет свойство переменной, см.

residue Функция позволяет вычислять вычеты на rest Функция выделяет остаток после удаления reverse Функция меняет порядок элементов в списке на обратный, см. стр. rhs Функция выделяет правую часть уравнения, см. стр. 88– romberg Функция численно находит определенный rk Функция реализует метод Рунге-Кутта решения ОДУ, см. стр. row Функция выделяет заданную строку матрицы, см. стр. 43– save сохраняет текущие значения рабочей области в файл, см. стр. solve Функция решает уравнения и системы sort Функция упорядочивает элементы списка, Функция или Краткое описание переменная sublist Функция составляет список из тех элементов исходного списка, для которых заданная логическая функция возвращает значение true.

submatrix Функция выделяет из матрицы подматрицу, 43– subst Функция Реализует синтаксическую подстановку, см. стр. Sum Функция реализует цикл суммирования, taylor Функция Возвращает разложение функции tlimit Функция отличается от функции limit только алгоритмом она использует разложение выражения в ряд Тейлора, см.

totalfourier Функция позволяет вычислить построить translate Функция транслирует функцию Maxima на transpose Функция транспонирует матрицу, см.

trigexpand Переменная управляет работой функции trigexpand Функция раскладывает все тригонометрические функции от сумм в суммы произведений тригонометрических функций, см.

8.5. Решение обыкновенных дифференциальных уравнений Функция или Краткое описание переменная trigreduce Функция свертывает все произведения тригонометрических функций в тригонометрические функции от сумм, см. стр. 61– trigsimp Функция только применяет к выражению trirat Функция пытается свести выражение с тригонометрическими функциями к некому универсальному каноническому виду (в общем, пытается упростить выражение), см.

uniteigenvectors Функция отличается от функции eigenvectors тем, что возвращает нормированные на единицу собственные writele Функция начинает запись выходных данных Maxima в указанный файл, см. стр. write_matrix, функция для вывода массивов чисел, см.

zeromatrix Функция возвращает матрицу заданной ’’ Две одиночные кавычки ’’a вызывают дополнительное вычисление в момент обработки a, см. стр. ’ Одиночная кавычка ’ предотвращает вычисление, см. стр. Таблица 2: Перечень основных пакетов расширения Maxima Наименование Краткое описание функций пакета пакета augmented_lagran- Минимизация функции нескольких переgian менных с ограничениями методом неопределённых множителей Лагранжа (используется совместно с lbfgs) bode Построение диаграмм Боде (узкоспециальный пакет) contrib_ode Дополнительные функции для аналитического решения обыкновенных дифференциальных уравнений descriptive Описательная статистика, оценка параметров распределения (генеральной совокупности) по выборке (см. стр. 261–270) distrib Пакет, содержащий функции для расчёта draw Интерфейс Maxima-Gnuplot. Предназначен для подготовки иллюстраций полиграфического качества Dynamics Различные функции, в т.ч. графические, относящиеся к моделированию динамических систем и фракталов 8.5. Решение обыкновенных дифференциальных уравнений Наименование Краткое описание функций пакета пакета позволяющую оперировать с производящими функциями последовательностей (узкоспециальный пакет) graphs Пакет, включающий функции для работы с grobner Функции для того, чтобы работать с базисом Грёбнера (Groebner) Impdi вычисление производных неявных функций implicit_plot Графики неявных функций interpol Пакет, включающий функции интерполяции (линейной, полиномами Лагранжа, lapack Функции пакета Lapack для решения задач Lbfgs пакет минимизации функций нескольких lindstedt Пакет, рассчитанный на интерпретацию lsquares Функции для оценки параметров различных зависимостей методом наименьших makeOrders Пакет включает одну функцию для операций с полиномами mnewton Метод Ньютона для решения систем нелинейных уравнений Наименование Краткое описание функций пакета пакета numericalio Чтение и запись файлов (преимущественно opsubst Пакет содержит одну функцию opsubst, позволяющую выполнять замену в выражениях (по возможностям мало отличается от orthopoly Пакет, содержащий функции для операций с ортогональными полиномами (Лежандра, plotdf Пакет, позволяющий строить поле направлений для решения автономных систем (интересный, но довольно узкоспециальный romberg Пакет, включающий ряд функций для численного интегрирования simplex Пакет, предназначенный для решения задач линейного программирования solve_rec Пакет, содержащий функции для упрощения рекуррентных выражений stats Пакет, включающий функции для статистической проверки гипотез (о равенстве stirling Расчёт гамма-функции stringproc Пакет, включающий функции для обработки строк unit Пакет, включающий функции для операций 8.5. Решение обыкновенных дифференциальных уравнений Наименование Краткое описание функций пакета пакета zeilberger Функции для гипергеометрического суммирования Таблица 3: Список основных математических констант, доступных в Maxima Обозначение в Математическое содержание Maxima inf положительная бесконечность (на действительной оси) minf отрицательная бесконечность (на действительной оси) innite бесконечность (на комплексной плоскости) false, true логические (булевы) величины Таблица 4: Список основных математических функций, доступных в Maxima Обозначение в Математическое содержание Maxima acosh обратный гиперболический косинус asinh обратный гиперболический синус atanh обратный гиперболический тангенс ceiling округление до целого с избытком oat преобразование к формату с плавающей 8.5. Решение обыкновенных дифференциальных уравнений Обозначение в Математическое содержание Maxima Литература [1] Документация по текущей версии пакета: http://maxima.

sourceforge.net/docs/manual/en/maxima.html [2] В. А. Ильина, П. К. Силаев. Система аналитических вычислений Maxima для физиков-теоретиков. М.:МГУ им. М. В. Ломоносова, 2007. 113 с. http://tex.bog.msu.ru/numtask/max07.ps [3] Статьи Тихона Тарнавского http://maxima.sourceforge.net/ ru/maxima-tarnavsky-1.html [4] http://www.pmtf.msiu.ru/chair31/students/spichkov/ maxima2.pdf (Методическое пособие по изучению математического пакета Maxima) Математический практикум с применением пакета Maxima. (PDF) [5] Н. А. Стахин. Основы работы с системой аналитических (символьных) вычислений MAXIMA (ПО для решения задач аналитических (символьных) вычислений). Москва: Федеральное агентство по образованию, 2008 86 с.

[6] Книга по Maxima (электронное руководство) http://maxima.

[7] Книга Gilberto E. Urroz http://www.neng.usu.edu/cee/faculty/ gurro/Maxima.html [8] В. З. Аладьев. Системы компьютерной алгебры: Maple: искусство программирования / В. З. Аладьев. М.: Лаборатория базовых знаний, 2006. 792 с.

[9] А. Н. Васильев. Mathcad 13 на примерах / А. Н. Васильев. СПб.:

БХВ-Петербург, 2006. 528 с.

Глава 8. Литература [10] Е. М. Воробъев. Введение в систему символьных, графических и численных вычислений Mathematica 5 / Е. М. Воробъев. М.:

ДИАЛОГ-МИФИ, 2005. 368 с.

[11] В. Н. Говорухин. Введение в Maple. Математический пакет для всех / В. Н. Говорухин, В. Г. Цибулин. М.: Мир, 1997. 208 с.

[12] Д. А. Гурский. Вычисления в MathCAD / Д. А. Гурский. Мн.:

Новое знание, 2003. 814 с.

[13] Д. А. Гурский. Mathcad для студентов и школьников. Популярный самоучитель / Д. А. Гурский, Е. Турбина. СПб.: Питер, [14] В. П. Дьяконов. Maple 9 в математике, физике и образовании / В. П. Дьяконов. М.: СОЛОН-Пресс, 2004. 688 с.

[15] В. П. Дьяконов. Справочник по MATHCAD PLUS 7.0. PRO / В. П. Дьяконов. М.: СК Пресс, 1998. 352 с.

[16] В. Ф. Очков. Mathcad 12 для студентов и инженеров / В. Ф. Очков. СПб.: БХВ-Петербург, 2005. 464 с.

[17] А. И. Плис. MATHCAD 2000. Математический практикум для экономистов и инженеров / А. И. Плис, Н. А. Сливина. М.: Финансы и статистика, 2000. 656 с.

[18] А. М. Половко. Derive для студента / А. М. Половко. СПб.:

БХВ-Петербург, 2005. 352 с.

[19] А. М. Половко. Mathcad для студента / А. М. Половко, И. В. Ганичев. СПб.: БХВ-Петербург, 2006. 336 с.

[20] О. А. Сдвижков. Математика на компьютере: Maple 8 / О. А. Сдвижков. М.: СОЛОН-Пресс, 2003. 176 с.

[21] Новые информационные технологии: Учеб. пособие / Под ред.

В. П.,Дьяконова; Смол. гос. пед. ун-т. Смоленск, 2003.

Ч. 3: Основы математики и математическое моделирование / В. П. Дьяконов, И. В. Абраменкова, А. А. Пеньков. 192 с.: ил.

[22] Р. В. Майер. Решение физических задач с помощью пакета MathCAD [Электронный ресурс] / Р. В. Майер. Глазов: ГГПИ, 2006. 37 c. http://maier-rv.glazov.net/math/math1.htm [23] Б. Я. Советов, С. А. Яковлев. Моделирование систем.

[24] П. Эйкхофф. Основы идентификации систем управления.

[25] В. Дьяконов, В. Круглов. Matlab: Анализ, идентификация и моделирование систем. СПб.:Питер,2001. 444 с.

[26] В. К. Морозов, Г. Н. Рогачёв. Моделирование информационных и динамических систем. М.: ИЦ Академия, 2011. 384 с.

[27] А. В. Антонов. Системный анализ. Учеб. для вузов. М.: Высш.

Предметный указатель арифметические операции, 29 необходимое условие, алгебраическая форма, 78 интегрирование экспоненциальная форма, 81 changevar, тригонометрическая форма, дифференциальные уравнения, ряды однородные уравнения, 164 степенной ряд, уравнение Бернулли, 168 точки разрыва, компьютерная алгебра, 10 динамические системы, алгоритмы компьютерной ал- аттрактор, характеристический полином, программирование ортогонализация, 87 простейшие команды, Предметный указатель reverse, точность вычислений, тригонометрические выражения, trigexpand, trigrat, trigreduce, уравнения обратная матрица, решение, allroots, linsolve, realroots, ввод-вывод файловые матрицы, в консоли, oat, kill, wxMaxima, Компьютерная математика с Maxima: Руководство для Оформление обложки: А. Осмоловская Подписано в печать 10.05.12. Формат 60×90/16.

Гарнитура Computer Modern. Печать офсетная. Бумага офсетная.

Усл. печ. л. 24,0. Уч.-изд. л. 18,22. Тираж 999 экз. Заказ Адрес для переписки: 119334, Москва, 5-й Донской проезд, д.15, Телефон: (495) 662-38-83. E-mail: sales@altlinux.ru

«1 Научная деятельность МГТУ МАМИ традиционно ориентирована на автомобиле- и тракторостроение, смежные отрасли промышленности. За последние десятилетия внедрено более 600 научно-технических разработок университета. Ряд разработок отмечен государственными и правительственными премиями, наградами международных выставок. Большинство разработок защищено авторскими правами. Материал каталога изложен в трех тематических разделах: Конструкторские разработки, Технология, оборудование и материалы и. »

«Все ЕТКС в одном месте! Документ скачен с сайта ALLETKS.RU. Навещайте наш сайт почаще! Единый тарифно-квалификационный справочник работ и профессий рабочих Выпуск 5 Раздел Геологоразведочные и топографо-геодезические работы (утв. постановлением Минтруда РФ от 17 февраля 2000 г. N 16) Содержание Введение Раздел Геологоразведочные и топографо-геодезические работы Алфавитный указатель профессий рабочих Введение Настоящий выпуск Единого тарифно-квалификационного справочника работ и профессий. »

«МИНИСТЕРСТВО СЕЛЬСКОГО И ВОДНОГО ХОЗЯЙСТВА ТАШКЕНТСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ 5630100 – направление Механизация сельского хозяйства ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА на тему: Усовершенствование рабочего органа для сбора с кустов остатков урожая хлопка Руководитель ВКР, доцент Горлова И. Г. Выполнил : студент IV курса 85гр. Тайманова.А.К. ВКР рассмотрена и допущена к защите: Зав. кафедрой ЭМТП и ТС Декан факультета МСХ Халилов Р.Д. _ доц. Фармонов Э.Т. _2013 год 2013 год Ташкент. »

«ТЕХНИЧЕСКИЙ БЮЛЛЕТЕНЬ Регулирующие клапаны Valtek Mark One FCD VLRUTB0001-30 11/09 (Вместо FCD-VLATB001) Регулирующие клапаны Valtek Mark One FCD VLRUTB0001 – 11/09 Корпус клапана в сборе Поршневой привод с большим перестановочным усилием: Три стандартных типоразмера соответствуют большинству возможных условий Возвратная эксплуатации. Вид действия пружина легко изменить с прямого на обратный. Приводы имеют повышенную жесткость и обеспечивают высокую стабильность характеристик и O малый. »

«Мезенцев С.А. КАК ОЗДОРОВИТЬ ЧЕЛОВЕКА, МЕДИЦИНУ И ОБЩЕСТВО (Стратегия выживания и система особой заботы о жизни и здоровье человека и общества) ПОЯСНЕНИЯ ПО ЭЛЕКТРОННОЙ ВЕРСИИ КНИГИ 1. Электронная версия данной книги редуцирована примерно на 2/3 от того объёма информации, который есть в её полиграфическом прототипе. Это уменьшение объёма необходимо для экономии времени пользователей при их знакомстве с данной работой с помощью электронной почты. В связи с этим оно коснулось и текстовой части. »

«Информационные технологии в криминалистике ПРИЗНАКИ МОНТАЖА И ДРУГИЕ ИЗМЕНЕНИЯ В ЦИФРОВЫХ ФОНОГРАММАХ И ФОТОГРАФИЯХ И.Ю.Фетняев(Государственный экспертно-криминалистический центр МВД Республики Беларусь) Развитие и широкое распространение компьютерных средств обработки и монтажа цифровых записей, доступность детальной информации о выполнении таких действий на сегодняшний день привели к ситуации, когда создание поддельной фонограммы или фотографии может оказаться простой задачей даже для. »

«РАЗРАБОТЧИК ИП БОГДАНОВ А.А. УТВЕРЖДАЮ: Администрация муниципального образования Удаченский сельсовет Глава _Шинкарёв С.И. М.П. СХЕМА ВОДОСНАБЖЕНИЯ И ВОДООТВЕДЕНИЯ МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ УДАЧЕНСКИЙ СЕЛЬСОВЕТ АХТУБИНСКОГО РАЙОНА АСТРАХАНСКОЙ ОБЛАСТИ НА ПЕРИОД С 2014 ПО 2024 ГГ. 2014г. 1 Содержание. ВВЕДЕНИЕ 7 ПАСПОРТ СХЕМЫ 1.ВОДОСНАБЖЕНИЕ 1.1Технико-экономическое состояние централизованных систем водоснабжения. 1.1.1Система и структура водоснабжения с делением территорий на эксплуатационные. »

«TRUCKNOLOGY® GENERATION A (TGA) Издание 2012 Bepcия 1.1 Издатель MAN Truck & Bus AG ( д а л ее по т екс т у им енуемый MAN) О тдел SMTST D a c h a u e r S t r. 667 D — 80995 Mnchen E- M a il: esc@man.eu Фа кс: + 4 9 ( 0 ) 8 9 15 8 0 4 2 6 4 www.manted.de МAN сохраняет за собой право внесения технических изменений, основанных на дальнейших конструкторских разработках. © 2012 MAN Truck & Bus Aktiengesellschaft Перепечатка, размножение или перевод данного руководства, в том числе его отдельных. »

«1 Примечание сетевого публикатора. Сканировал книгу не я, сканы, низкого качества, взяты в сети В книге было много фотографий, их пришлось убрать т.к. разобрать на них ничего нельзя. Подписи к фотографиям я оставил, они выделены желтым фоном. Схемы, т.е. штриховые рисунки, я оставил, т.к. на них все же можно что-то разобрать. 2 N. P. BECHTEREVA MAGIC SPELL OF THE BRAIN & LABYRINTHS OF LIFE St.Petersburg Notabene Publishers 1999 Н. П. БЕХТЕРЕВА МАГИЯ МОЗГА И ЛАБИРИНТЫ ЖИЗНИ Санкт-Петербург. »

«novdocx (ru) 12 May 2009 Приложение User Application: руководство пользователя Novell® Модуль обеспечения правами доступа на основе ролей Identity Manager 3.7 18 сентября 2009 r. www.novell.com Модуль обеспечения правами доступа на основе ролей Identity Manager: руководство пользователя novdocx (ru) 12 May 2009 Юридическая информация Компания Novell, Inc. не дает никаких гарантий или обещаний относительно содержания или возможностей использования данной документации, особо оговаривая отказ от. »

«Экосистемы, их оптимизация и охрана. 2011. Вып. 5. С. 11–20. Флора и фауна УДК 581.526.65 (477) ИЗУЧЕНИЕ СЕГЕТАЛЬНОЙ РАСТИТЕЛЬНОСТИ УКРАИНЫ С ПОЗИЦИЙ ЭКОЛОГО-ФЛОРИСТИЧЕСКОГО ПОДХОДА: ИСТОРИЯ, СОВРЕМЕННОЕ СОСТОЯНИЕ, ПЕРСПЕКТИВЫ Багрикова Н. А. Никитский ботанический сад – Национальный научный центр НААНУ, Ялта, nbagrik@ukr.net Представлен исторический обзор синтаксономических исследований сегетальной растительности Украины с позиций метода Браун-Бланке за период 1981–2011 годы. Ключевые слова. »

«ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЁВА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ) ТЕЛЕФОННЫЙ СПРАВОЧНИК СГАУ 2012 САМАРА Содержание Ректорат 1 4 Общественны е организации 2 7 Учебны е институты и филиалы 3 Факультеты. Приёмная комиссия 4 Кафедры 5 Научны е подразделения 6 НИИ Центры ОНИЛ НИЛ НИГ НГ СКБ НОЦ Общие университетские подразделения 7. »

«НАШИ РЕЗУЛЬТАТЫ И РЕКОМЕНДАЦИИ ЦЕНТРАЛЬНЫЙ ФЕДЕРАЛЬНЫЙ ОКРУГ УРОЖАЙНОСТЬ 2013-2014 КУКУРУЗА ПОДСОЛНЕЧНИК ВВЕДЕНИЕ КАЧЕСТВО MASAdOuR SeMeNceS : МЫ пРЕДЛАгАЕМ ВАМ эЛИТНУю гЕНЕТИКУ, пРОВЕРЕННУю И АДАпТИРОВАННУю ДЛя ВАШЕгО РЕгИОНА Masadour Semences ставит перед собой единственную основную цель: предоставлять Вам элитную генетику и высококачественные семена, адаптированные к условиям Вашего региона! Прежде чем выпустить продукт на рынок, его качество проверяется более чем в 250 точках испытаний в. »

«ПРИМЕРНАЯ ПРОГРАММА ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ по направлению ТЕХНОЛОГИЯ. ТЕХНИЧЕСКИЙ ТРУД ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Статус документа Примерная программа по направлению Технология. Технический труд составлена на основе федерального компонента государственного стандарта основного общего образования. Примерная программа позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного. »

«Издание ГПНТБ России день за днем предоставляет своим читателям информацию о событиях, связанных с деятельностью крупнейшей научно-технической библиотеки страны, которые произошли в течение последних месяцев. В первом номере приводится хроника событий в период с октября по декабрь 2009 г. Дайджест рассказывает (с иллюстрациями) о международной деятельности библиотеки: конференциях, выставках, встречах с издательствами, проводимых библиотекой, участии сотрудников ГПНТБ России в наиболее значимых. »

«ВЫСШЕЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ Б. А. БУЗОВ, Г. П. РУМЯНЦЕВА МАТЕРИАЛЫ ДЛЯ ОДЕЖДЫ Рекомендовано Учебно методическим объединением вузов России по образованию в области технологии, конструирования изделий легкой промышленности в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальностям Технология швейных изделий и Конструирование швейных изделий и направлению Технология, конструирование и материалы изделий легкой промышленности 1 УДК 687.1(075.8) ББК. »

«MultiSync EA244WMi Руководство пользователя Алфавитный указатель Предупреждение, Внимание Информация о регистрации Рекомендации по эксплуатации Содержимое Краткое руководство по началу работы Органы управления Технические характеристики Характеристики Устранение неисправностей Функция Автояркость ControlSync Дисплеи, сертифицированные TCO 6 Информация производителя о потребляемой энергии и утилизации ПРЕДУПРЕЖДЕНИЕ ВО ИЗБЕЖАНИЕ ВОЗГОРАНИЯ ИЛИ ПОРАЖЕНИЯ ЭЛЕКТРИЧЕСКИМ ТОКОМ НЕ ПОДВЕРГ АЙТЕ. »

«148 современников. Анализ творчества. Сост., Жизнеописание, примечания Н.Н. Заболоцкого. М., 1995. 3 — Тихвинская Л.И. Кабаре и театры миниатюр в России. 1908-1917. М., 9 1995. СФЕРА РАЗУМА В.И. ВЕРНАДСКОГО И СОКРОВЕННАЯ ЗЕМЛЯ А.П. ПЛАТОНОВА КАБарщт Очевидно, наступил момент, когда можно окончательно отбросить снисходительную улыбку при рассмотрении научно-философских концепций А. Платонова, принимая его как писателя-философа, равно­ го Ф.М. Достоевскому и Л.Н. Толстому. Это необходимо сделать. »

«МЕТОДИКА ОЦЕНКИ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ ПРИ ПРЕДОСТАВЛЕНИИ МЕР ГОСУДАРСТВЕННОЙ ПОДДЕРЖКИ Воронеж 2011 1 СПИСОК ИСПОЛНИТЕЛЕЙ Научный руководитель, Туровец О.Г. д.э.н., профессор (подпись, дата) Ответственный исполнитель, Родионова В.Н. д.э.н., профессор (подпись, дата) Исполнители темы: к.э.н., доцент Дударева О.В. д.э.н., профессор Гунина И.А. к.э.н., доцент Шишкин И.А. СОДЕРЖАНИЕ 1. Общие положения 2. Методика оценки инвестиционных проектов при предоставлении мер государственной поддержки № 3. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ (РОСТЕХРЕГУЛИРОВАНИЕ) ФГУП “РОССИЙСКИЙ НАУЧНО-ТЕХНИЧЕСКИЙ ЦЕНТР ИНФОРМАЦИИ ПО СТАНДАРТИЗАЦИИ, МЕТРОЛОГИИ И ОЦЕНКЕ СООТВЕТСТВИЯ” (ФГУП “СТАНДАРТИНФОРМ”) Рег. № 3395 ОРГАНИЗАЦИЯ ПО ПРОДОВОЛЬСТВИЮ И СЕЛЬСКОМУ ХОЗЯЙСТВУ ООН МЕЖДУНАРОДНЫЕ СТАНДАРТЫ ПО ФИТОСАНИТАРНЫМ МЕРАМ РУКОВОДСТВО ПО УСТАНОВЛЕНИЮ И ПРИЗНАНИЮ ЭКВИВАЛЕНТНОСТИ ФИТОСАНИТАРНЫХ МЕР GUIDELINES FOR DETERMINATION AND RECOGNITION OF EQUIVALENCE OF PHYTOSANITARY MEASURES. »

© 2014 www.kniga.seluk.ru — «Бесплатная электронная библиотека — Книги, пособия, учебники, издания, публикации»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Тихон Тарнавский. Maxima. Алгебра и начала анализа

Из встроенного функционала Maxima в первую очередь стоит обратить внимание на несколько групп функций: работу с пределами, дифференцирование, интегрирование, поиск решений уравнений — как «просто», так и дифференциальных.

«Предельничаем»…

Собственно полноценных функций для нахождения предела существует в Maxima аж одна. Но зато какая! Она может принимать три различных варианта списка аргументов, и кроме того, на ее действие влияют еще и три флага. Но давайте по порядку. Зовут эту функции вполне соответственно ее действию: limit ; и в самом стандартном варианте ее вызов выглядит как limit(выражение, переменная, точка) , то есть то, что в математической записи выглядит как lim _{x → a} f ( x ), в контексте Maxima запишется как limit(f(x), x, a) :

Maxima может искать пределы не только в конечных точках, но и на бесконечности. Среди стандартных обозначений программы существуют универсальные названия для разных бесконечностей: плюс-бесконечность записывается через inf (от слова infinity, как нетрудно догадаться), минус-бесконечность — через minf (от minus infinity); для комплексных чисел бесконечность, как известно, одна, и она (комплексная бесконечность) обозначается полным словом infinity . При работе с пределами все три обозначения могут как использоваться при вводе, так и возникать в виде найденного значения предела; отдельно здесь надо отметить один момент касательно работы с интерфейсом к Maxima в редакторе TeXmacs: символы inf и minf при выводе здесь отображаются в своей традиционной математической нотации, то есть как ∞ и −∞; символ вместо inf можно, кроме того, использовать еще и при вводе.

Второй вариант вызова функции limit() — это расширенная версия первого: limit(выражение, переменная, точка, направление) , для поиска односторонних пределов. Для предела справа в качестве «направления» указывается plus , для предела слева — minus :

Пределы справа и слева еще иногда называют соответственно пределами сверху и снизу. Хотя правильнее в таком случае говорить полностью: «предел при x , стремящемся к a сверху», в том числе чтобы не создавать путаницы с верхним и нижним пределами, которые суть совершенно другое.

Кроме упомянутых выше бесконечностей, на выходе возможно появление и еще двух обозначений, на случай, если заданный предел не существует: ind (от слова indefinite — неопределенный) и und (от слова undefined — опять же неопределенный). В документации первое из этих обозначений описано как indefinite but bounded (не определен, но ограничен), что дает предположить, что функция, не имеющая предела, при этом ограничена либо в окрестности предельной точки, либо на всей прямой. Какое из этих предположений имелось в виду, мне так и не удалось понять, потому как на практике ни одно из них не соответствует действительности. Вывода ind мне не удалось добиться ни на одной функции, радикально отличающейся от «канонической» (в том смысле, что фигурирующей в стандартном примере из комплекта) функции sin(1/x) .

Здесь все правильно, tan(1/x) не ограничена в окрестности нуля. А вот дальше начинаются чудеса:

Как видите, первая функция имеет конечные односторонние пределы в нуле, а вторая ограничена вообще на всей оси — и тем не менее… Но это, думаю, не столь критично: главное, что наличие любого из этих символов в качестве вывода дает нам понять, что искомого предела не существует.

Функция limit() в третьем варианте — limit(выражение) — предназначена уже не для поиска собственно пределов, а для упрощения выражений, содержащих символы inf и minf :

Выражения такого рода могут возникать, к примеру, при подстановках в формулы результатов вычисления каких-то других пределов или интегралов.

Такая способность — принимать различные списки аргументов — не является в Maxima чем-то особенным; она свойственна очень многим встроенным функциям, как и различное действие в зависимости от значений разнообразных переключателей. Это достаточно удобно: не нужно запоминать много разных имен функций (для поиска пределов, к примеру, используется исключительно функция limit ); для вычисления производных, в том числе и частных, — функция diff (с которой мы уже бегло ознакомились в первой статье и сейчас продолжим это знакомство); для нахождения интегралов, как определенных, так и неопределенных — функция integrate (с которой мы тоже сегодня познакомимся). Имена наиболее часто используемых функций запомнить несложно, а о дополнительных ключах или флагах, в случае чего, можно прочитать во встроенной справке, набрав ? имя-функции .

Об этих самых ключах к функции limit и осталось рассказать. Первый ключ называется lhospitallim и задает максимальное количество применений правила Лопиталя; название ключа и происходит от фамилии ученого, давшей название самому правилу, которая в оригинале пишется как L’Hospital. Напомню, правило это гласит, что в случае неопределенности вида 0/0 или можно продифференцировать числитель и знаменатель — и предел от этого не изменится. Ограничитель количества применений этого правила нужен для того, чтобы избежать зацикливаний, которые могут случиться для бесконечно дифференцируемых функций, у которых в данной точке равны нулю либо бесконечности все производные. По умолчанию значение lhospitallim равно четырем, и мне не удалось сходу придумать пример, когда этого не хватает — ведь функция поиска предела использует не только правило Лопиталя, но и другие соотношения; и для всех заданных мною соотношений двух функций с корнями выше четвертого порядка в искомой точке предел был успешно найден и при умолчательном значении.

Второй ключ к функции limit — это флаг limsubst , который, будучи выставлен в true , позволяет этой функции производить подстановки внутрь неизвестных выражений. По умолчанию этот флаг равен false , что исключает ошибки вроде такой:

И, наконец, последний дополнительный параметр — еще один флаг, по имени tlimswitch . По умолчанию он тоже выключен, а если его включить, функция limit будет, при невозможности найти предел другими способами, пытаться его найти путем разложения подпредельной функции в ряд Тейлора в окрестности заданной точки:

Но в случае поиска односторонних пределов, в тех точках, где они не равны между собой, то есть полного предела не существует, этим флагом нужно пользоваться с осторожностью: при его включении функция limit может вернуть в качестве полного предела один из односторонних:

Реально у этой функции в точке ноль только предел справа равен единице; а предел слева — нулю.

И последнее: почему я употребил в начале по отношению к функции limit() слово «полноценная». Потому что кроме нее существует еще одна «недофункция» — tlimit() ; она представляет собой фактически просто-напросто вызов самой функции limit() с поднятым флагом tlimswitch , то есть пытается при необходимости разложить «подпредельную» функцию в ряд Тейлора вне зависимости от реального значения этого флага. Другими словами вызов tlimit(аргументы) полностью аналогичен записи limit(аргументы) , tlimswitch:true ; только чуть короче. И аргументы она может принимать точно такие же.

…дифференцируем и интегрируем

О функции diff я кое-что уже рассказывал в первой статье, и здесь это «кое-что» только напомню. В двух упомянутых тогда вариантах вызова эта функция принимала один либо два аргумента. С двумя, diff(выражение, переменная) , она возвращает производную от «выражения» по заданной переменной; с одним, diff(выражение) — полный дифференциал заданного выражения. Другими словами, запись diff(f, x) равнозначна математическому обозначению d f /d x , а diff(f) — d f .

Но это еще не все. Кроме одного либо двух, эта функция может также принимать любое нечетное число агрументов вида diff(выражение, переменная, порядок, переменная, порядок, …) и возвращает при этом производную либо смешанную частную производную от выражения заданных порядков по заданным переменным. К примеру, diff(f, x, 3) означает d 3 f /d x 3 , а diff(f, x, 1, y, 2, z, 1) — d 4 f /d x d y 2 d z . Единственный флаг, имеющий прямое отношение к самой функции diff — это флаг derivabbrev, который влияет на отображение производных в ячейках вывода Maxima. По умолчанию он равен false , и производные обозначаются в виде дробей с буквой d; если же его выставить в true , производные будут отображаться в сокращенном виде, с переменными дифференцирования записанными в виде индексов:

Кроме того, функция diff используется еще и для обозначения производных в дифференциальных уравнениях. Но об этом чуть позже, а сейчас перейдем к интегрированию.

Основная функция интегрирования называется, как я уже говорил, integrate и имеет два варианта вызова: для нахождения неопределенного и определенного интегралов. Первый выглядит как integrate(выражение, переменная) , второй — как integrate(выражение, переменная, нижний-предел, верхний-предел) :

Вы, наверное, обратили внимание еще на один момент в ячейках %i4 – %o4 . Когда в выражении используется какой-либо независимый символ, результат, вообще говоря, может зависеть от значения этого символа. Если при этом о возможных значениях символа ничего не известно, то Maxima задаст вам один или несколько вопросов об этом значении, и решение будет искать в зависимости от ваших ответов на них. Так, в этом примере значение определенного интеграла напрямую зависит от знака параметра a:

Кроме обычных определенных интегралов Maxima умеет искать также и несобственные интегралы, то есть такие, у которых неограничена либо область интегрирования, либо подынтегральная функция; и делается это все той же функцией integrate :

В случае, если искомый интеграл не сходится, будет выдано сообщение об ошибке, говорящее о том, что интеграл расходящийся:

В случае, если интеграл не может быть найден, он либо целиком возвращается в несовершенном виде, либо упрощается частично и на выходе получается некоторая формула, включающая в несовершенном виде интеграл той части подынтегрального выражения, которую проинтегрировать не удалось:

Кроме функций diff и integrate , в Maxima есть еще много разнообразных возможностей, связанных с производными и интегралами, в частности, функции для численного расчета значений определенных интегралов, а также инструменты, применимые при работе с дифференциальными и интегральными уравнениями. И разнообразны они настолько, что для того, чтобы рассмотреть подробно и с примерами их все, не хватило бы всего этого цикла. А более тезисно, хотя и на английском языке, они описаны в документации. Посему с этой темой на этом прекращаем и движемся дальше.

Решайте, сударь!

А дальше мы рассмотрим уравнения и их системы, и даже не столько рассмотрим, сколько порешим… то есть, конечно, порешаем. Уравнения и системы уравнений решаются в Maxima тоже одной и той же функцией, и тоже уже вам слегка знакомой по первой статье: это функция solve . Но прежде чем рассмотреть ее подробнее, нужно сказать пару слов о списках, или векторах, в Maxima; поскольку именно в виде списков solve возвращает корни, да и принимает параметры в случае решения системы уравнений, а не одного уравнения.

Синтаксис списков в Maxima весьма прост; это перечисление элементов в квадратных скобках: [элемент1, элемент2, …, элементN] . Особенность — не в синтаксисе. Основное достоинство Maximaльных списков в том, что их элементами могут быть совершенно любые выражения: символы, арифметические выражения, вызовы функций, присвоения, уравнения, другие списки… Додумать можете сами. Поэтому списки и во встроенных функциях применяются достаточно широко. Функция solve в своем простейшем варианте, для решения одиночного уравнения, в качестве аргументов никаких списков, напомню, не принимает (а принимает либо уравнение и символ, относительно которого его надо решать, либо только уравнение, если символ в нем всего один). А вот в качестве результата она уже и в таком варианте возвращает список, состоящий из всех корней заданного уравнения:

Как видите, функция solve находит все комплексные корни уравнения, а не только действительные.

К элементу списка можно обратиться с помощью тех же квадратных скобок, указав в них номер элемента после имени списка. Напомню, что равенство, переданное в качестве дополнительного параметра функции ev, означает подстановку переменной в вычисляемое выражение. Вот так мы можем осуществить проверку решения, подставив корень из выданного списка в исходное уравнение:

Точно таким же образом можно обратиться и к любому другому элементу списка:

Вообще говоря, в качестве первого аргумента функции solve можно задавать не только уравнение, а вообще любое выражение. При этом «корни выражения» (не являющегося уравнением) ищутся в том самом смысле, в каком эта фраза понимается в математике: корни выражения — это те значения переменной, на которых выражение обращается в ноль. Возможность такой записи позволяет, к примеру, легко найти критические точки любой непрерывной функции (а заодно и вычислить значения функции в этих точках):

В этом примере есть еще два важных момента. Первый — функция %th() . Она, как видно из контекста, вызывается как %th(n) и возвращает n -ю с конца ячейку вывода. Это, так же как и обозначения % и _ , удобно, чтобы не обращать внимания на номера ячеек, и кроме того, применимо в командных файлах Maxima, которые могут загружаться в том числе и прямо из интерактивной сессии (с помощью функции load ) — и тогда просто заранее неизвестно, начиная с какой ячейки данный файл загружен. И второй момент: здесь проиллюстрировано, что в Maxima операция индексирования списка доступна не только по отношению к именам переменных, но и к вызовам функций; другими словами, если функция возвращает список значений, мы можем выбрать одно конкретное из них, написав его номер в квадратных скобках прямо после вызова функции.

Вернемся к функции solve . А именно, перейдем теперь к решению систем уравнений. Для этого существует такой вариант записи: solve([уравнение1, уравнение2, …], [переменная1, переменная2, …]) ; либо сокращенный, аналогично варианту для одиночного уравнения: если количество уравнений и количество неизвестных равны, список неизвестных можно не писать: solve([уравнение1, уравнение2 …]) (не забудьте квадратные скобки, иначе Maxima примет его за вариант с одним уравнением).

Здесь возвращается список из нескольких списков, каждый из которых соответствует одному решению системы. В качестве подстановок можно использовать как такие списки целиком (например, в данном контексте, %o1[1] ), так и отдельные их элементы (например, %o1[1][1] ).

В случае, когда уравнений меньше, чем неизвестных, solve поступит точно так же, как и в случае одного уравнения с несколькими символами: все неуказанные будет воспринимать как параметры:

Если solve не находит точных решений, она может, как и integrate , вернуть уравнение или систему уравнений в некотором упрощенном виде, а может и самостоятельно попытаться решить систему численно:

В таком случае, если вам все же нужны точные значения корней (в аналитической записи), либо если они не найдены даже в числах, можно попробовать решить уравнения по очереди, выражая одно неизвестное через другое:

И подставляя в оставшиеся уравнения:

Теперь можем подставить обратно — и найти значения второй неизвестной, например, для первого и последнего корней из последнего списка:

Функция solve имеет довольно большое количество различных переключателей, из которых может пригодиться в своем не-умолчательном значении в первую очередь один: solveradcan . Умолчание здесь равно false , а выставив этот флаг в true , мы заставим solve , помимо его умолчательного поведения, применять radcan — функцию по упрощению показательных, логарифмических и степенных (с рациональными степенями) функций. Это делает работу функции solve более медленной (потому по умолчанию этот режим и выключен), но в некоторых случаях может помочь разрешить проблемы, которые без этого ключа приведут к невозможности найти точное решение.

И снова дифференцируем и интегрируем

Помимо «просто» уравнений, Maxima позволяет также решать и обыкновенные дифференциальные уравнения первого и второго порядка. Функций, непосредственно занимающихся решением таких уравнений, существует две. Первая из них занимается поиском частных решений линейных дифференциальных уравнений и систем таких уравнений; зовут ее desolve , от слов differential equation solve. Эта функция принимает два аргумента, первый из которых — уравнение либо список уравнений, а второй — соответственно одна переменная или список переменных. Если не заданы значения функций и/или их производных в нуле, то в найденном решении они просто отображаются в виде f(0) или

задать эти значения позволяет функция atvalue(выражение, переменная = точка, значение) ; то есть, в данном случае atvalue(f(x), x=0, значение) или atvalue(‘diff(f(x)), x=0, значение) . Производные в уравнениях и системах, решаемых с помощью этой функции, должны быть записаны непременно в виде ‘diff(f(x), x) , а не просто ‘diff(f, x) , а сами функции, соответственно, тоже в виде f(x) , а не f — нужно продемонстрировать зависимость функции от ее аргумента.

И конечно же, точно так же как для обычных уравнений и систем, здесь мы тоже можем проверить решение с помощью подстановки, но только надо еще дополнительно задать принудительное вычисление производных, так как в уравнениях они фигурируют в несовершенной форме:

Вторая функция из этой группы называется ode2 и предназначена она для решения обыкновенных дифференциальных уравнений первого и второго порядка; ее название происходит от фразы ordinary differential equations of 1st or 2nd order. Пишется она так: ode2(уравнение, зависимая-переменная, независимая-переменная) . Здесь уже независимая переменная указывается в списке параметров функции явно, и потому обозначения вида y(x) не нужны: и функция, и переменная обозначаются просто одиночными буквами. Также в отличие от предыдущей функции, ode2 ищет не частное, а общее решение. Произвольная константа в решении уравнения первого порядка обозначена через %c ; в решении уравнения второго порядка таких констант, естественно, две, и обозначаются они как %k1 и %k2 .

В дополнение к функции ode2 существуют три функции для поиска частных решений на основе полученных общих. Иначе говоря, эти функции, получая конкретные условия относительно значения функции-решения в заданной точке, находят исходя из этих значений соответствующие им величины интегральных констант. Одна из этих функций предназначена для обработки решения дифференциального уравнения первого порядка. Она называется ic1 (i от initial value — начальное значение; c от constant — константа; 1 от 1 st order — первого порядка) и принимает три аргумента: первый — само решение, в том виде, в котором его находит функция ode2 ; второй — значение независимой переменной ( x -координаты), третий — значение функции (зависимой переменной, у ) при этом значении x и возвращает частное решение, проходящее через точку с заданными координатами ( x , y ):

И две функции работают с решениями уравнений второго порядка. Так как в общем решении уравнения второго порядка фигурируют две независимые константы, то эти функции задают уже по два условия для поиска частного решения. Первая функция выглядит как ic2(общее решение, x, функция-в-точке-x, производная-в-точке-x) . Расшифровка названия аналогична предыдущей функции. Действует тоже аналогично ей, а в качестве второго условия задает значение производной в той же заданной точке:

И последняя функция называется bc2 (b от boundary value — граничное значение; а дальше все как в предыдущей). Ее аргументы: первым, как и в двух остальных вариантах, идет само общее решение, возвращенное функцией ode2 ; после него идут две пары значений: x ₀, y ₀, x ₁, y ₁, задающие две точки, через которые должен проходить график функции-решения:

Касательно дифференциальных уравнений все этими функциями и заканчивается, никаких дополнительных ключей к ним не предназначено.

В следующий раз мы поговорим о средствах построения графиков функций и о средствах автоматизации: условных операторах, циклах и управляющих условиях, налагаемых на различные символы и выражения.

Вопросы о Maxima или этого сайта: Списки рассылки

Математическая система Maxima

Операции математического анализа

Суммы

Для нахождения сумм предназначена функция sum. Синтаксис функции:

Sum(выражение, переменная, нижняя граница изменения переменной, верхняя граница изменения переменной)

Если присвоить последнему аргументу значение системной переменной положительной бесконечности «inf», то это станет признаком отсутствия верхней границы и будет рассчитываться бесконечная сумма. Так же бесконечная сумма будет рассчитываться, если присвоить аргументу «нижний предел изменения переменной» значения системной переменной отрицательной бесконечности «minf». Эти же значения используется и в других функциях математического анализа.

Произведения

Для нахождения конечных и бесконечных произведений используется функция product. Она имеет такие же аргументы, что и в функции sum.

Пределы

Для нахождения пределов используется функция limit.

limit(выражение, переменная, точка разрыва)

Если аргументу «точка разрыва» присвоить значение «inf», то это будет признаком отсутствия границы.

Для вычисления односторонних пределов используется дополнительный аргумент, который имеет значение plus для вычисления пределов справа и minus — слева.

Например, выполним исследование непрерывности функции arctg(1/(x — 4)). Эта функция неопределенна в точке x = 4. Вычислим пределы справа и слева:

Как видим, точка x = 4 является точкой разрыва первого рода для данной функции, поскольку существуют границы слева и справа, которые равняются соответственно -PI/2 и PI/2.

Дифференциалы

Для нахождения дифференциалов используется функция diff. Синтаксис функции:

diff(выражение, переменная1, порядок производной для переменной1 [,переменная2, порядок производной для переменной2,…])

где выражение — это функция, которая дифференцируется, второй аргумент является переменной, по которой нужно брать производную, третий (необязательный) — порядок производной (по умолчанию — первый порядок).

Вообще обязательным для функции diff является только первый аргумент. В таком случае функция возвращает дифференциал выражения. Дифференциал соответствующей переменной обозначается через del(имя переменной):

Как видим из синтаксиса функции, пользователь имеет возможность определить одновременно несколько переменных дифференцирования и задать порядок для каждой из них:

Если использовать параметрическую функцию, то форма записи функции изменяется: после имени функции записываются символы «:=», а обращение к функции осуществляется через ее имя с параметром:

Производная может быть вычислена в заданной точке. Это осуществляется так:

Функция diff используется также и для обозначения производных в дифференциальных уравнениях, о чем идет речь ниже.

Интегралы

Для нахождения интегралов в системе используется функция integrate. Для нахождения неопределенного интеграла в функции используются два аргумента: имя функции и переменная, по которой происходит интегрирование. Например:

В случае неоднозначного ответа Maxima может задать дополнительный вопрос:

Ответ должен содержать текст из вопроса. В данном случае, если значение переменной y больше «0», это будет «positive» (положительное), а иначе — «negative» отрицательное). При этом допускается ввод только первой буквы слова.

Для нахождения определенного интеграла в функции следует указать дополнительные аргументы: пределы интеграла:

Maxima допускает задания и бесконечных пределов интегрирования. Для этого для третьего и четвертого аргументов функции используются значения «-inf» и «inf»:

Для нахождения приближенного значения интеграла в численном виде, как отмечалось ранее, следует выделить результат в ячейке вывода, вызывать на ней контекстное меню и выбрать из него пункт «To Float» (преобразовать в число с плавающей точкой).

Способна система вычислять и кратные интегралы. Для этого функции integrate вкладываются одна в другую. Ниже приводятся примеры вычисления двойного неопределенного интеграла и двойного определенного интеграла :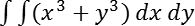

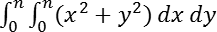
Решения дифференциальных уравнений

По своим возможностями в части решения дифференциальных уравнений Maxima ощутимо уступает, например, Maple. Но Maxima все же позволяет решать обычные дифференциальные уравнения первого и второго порядков, а также их системы. Для этого — в зависимости от цели — используют две функции. Для общего решения обычных дифференциальных уравнений используется функция ode2, а для нахождения решений уравнений или систем уравнений по начальным условиям — функция desolve.

Функция ode2 имеет такой синтаксис:

ode2(уравнение, зависимая переменная, независимая переменная);

Для обозначения производных в дифференциальных уравнениях используется функция diff. Но в этом случае с целью отображения зависимости функции от ее аргумента она записывается в виде ‘diff(f(x), x), а сама функция — f(x).

Пример. Найти общее решение обычного дифференциального уравнения первого порядка y’ — ax = 0.

Если значение правой части уравнения равняется нулю, то ее вообще можно опускать. Естественно, правая часть уравнения может содержать выражение.

Как видим, во время решения дифференциальных уравнений Maxima использует постоянную интегрирования %c, которая с точки зрения математики является произвольной константой, определяемой из дополнительных условий.

Осуществить решение обычного дифференциального уравнения можно и другим, более простым для пользователя, способом. Для этого следует выполнить команду Уравнения > Solve ODE (Решить обычное дифференциальное уравнение) и в окне «Решить ОДУ» ввести аргументы функции ode2.

Maxima позволяет решать дифференциальные уравнения второго порядка. Для этого также применяют функцию ode2. Для обозначения производных в дифференциальных уравнениях используется функция diff, в которой добавляют еще один аргумент — порядок уравнения: ‘diff(f(x), x, 2). Например решение обычного дифференциального уравнения второго порядка a·y» + b·y’ = 0 будет иметь вид:

Совместно с функцией ode2 можно использовать три функции, применение которых позволяет найти решение при определенных ограничениях на основании общего решения дифференциальных уравнений, полученного функцией ode2:

1. ic1(результат работы функции ode2, начальное значение независимой переменной в виде x = x₀, значение функции в точке x₀ в виде y = y₀). Предназначена для решения дифференциального уравнения первого порядка с начальными условиями.
2. ic2(результат работы функции ode2, начальное значение независимой переменной в виде x = x₀, значение функции в точке x₀ в виде y = y₀, начальное значение для первой производной зависимой переменной относительно независимой переменной в виде (y,x) = dy₀). Предназначена для решения дифференциального уравнения второго порядка с начальными условиями
3. bc2(результат работы функции ode2, начальное значение независимой переменной в виде x = x₀, значение функции в точке x₀ в виде y = y₀, конечное значение независимой переменной в виде x = x_n, значение функции в точке x_n в виде y = y_n). Предназначена для решения краевой задачи для дифференциального уравнения второго порядка.

Подробно с синтаксисом этих функций можно ознакомиться в документации к системе.

Выполним решение задачи Коши для уравнения первого порядка y’ — ax = 0 с начальным условием y(п) = 1.

Приведем пример решения краевой задачи для дифференциального уравнения второго порядка y»+y=x с начальными условиями y(o) = 0; y(4)=1.

Следует иметь в виду, что достаточно часто система не может решить дифференциальные уравнения. Например при попытке найти общее решение обычного дифференциального уравнения первого порядка 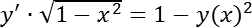получаем:

В таких случаях Maxima или выдает сообщение об ошибке (как в данном примере) или просто возвращает значение «false».

Другой вариант решения обычных дифференциальных уравнений первого и второго порядков предназначен для поиска решений с начальным условиями. Он реализуется с помощью функции desolve.

desolve(дифференциальное уравнение, переменная);

Если осуществляется решение системы дифференциальных уравнений или есть несколько переменных, то уравнение и/или переменные подаются в виде списка:

desolve([список уравнений], [переменная1, переменная2. ]);

Так же как и для предыдущего варианта, для обозначения производных в дифференциальных уравнениях используется функция diff, которая имеет вид ‘diff(f(x), x).

Начальные значения для переменной предоставляются функцией atvalue. Эта функция имеет такой синтаксис:

atvalue(функция, переменная = точка, значение в точке);

В данном случае предусматривается, что значения функций и (или) их производных задаются для нуля, потому синтаксис функции atvalue имеет вид:

atvalue(функция, переменная = 0, значение в точке «0»);

Пример. Найти решение дифференциального уравнения первого порядка y’=sin(x) с начальным условием.

Заметим, что и при отсутствии начального условия функция также сработает и выдаст результат:

Это позволяет осуществить проверку решения для конкретного начального значения. Действительно, подставляя в полученный результат значение y(0) = 4, как раз и получаем y(x) = 5 — cos(x).

Функция desolve дает возможность решать системы дифференциальных уравнений с начальными условиями.

Приведем пример решения системы дифференциальных уравнений 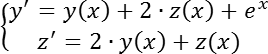с начальными условиями y(0) = 0; z(0) = 1.

Обработка данных

Статистический анализ

Система дает возможность рассчитать основные статистические описательные статистики, с помощью которых описываются наиболее общие свойства эмпирических данных. К основным описательным статистикам относят среднюю, дисперсию, стандартное отклонение, медиану, моду, максимальное и минимальное значение, размах вариации и квартили. Возможности Maxima в этом плане несколько скромны, но большинство этих статистик с ее помощью рассчитать достаточно просто.

Самым простым способом расчета статистических описательных статистик является использование палитры «Statistics» (Статистика).

Панель содержит ряд инструментов, сгруппированных в четыре группы.

1. Статистические показатели (описательные статистики):
   • mean (средняя арифметическая);
   • median (медиана);
   • variance (дисперсия);
   • deviation (среднее квадратичное отклонение).
2. Тесты.
3. Построение пяти типов графиков:
   • гистограмма (Histogram). Используется в первую очередь в статистике для изображения интервальных рядов распределения. Во время ее построения по оси ординат откладывают части или частоты, а на оси абсцисс — значения признака;
   • диаграмма рассеяния (диаграмма корреляции, поле корреляции, Scatter Plot) — график по точкам, когда точки не соединяются. Используется для отображения данных для двух переменных, одна из которых является факторной, а другая — результативной. С ее помощью осуществляется графическое представление пар данных в виде множества точек («тучи») на координатной плоскости;
   • ленточная диаграмма (Bar Chart) — график в виде вертикальных столбцов;
   • секторная, или круговая, диаграмма (Pie Chart). Такая диаграмма разделена на несколько сегментов-секторов, площадь каждого из которых пропорциональна их части;
   • коробочная диаграмма (коробка с усами, шкатулка с усами, Box Plot, box-and-whisker diagram). Именно она чаще всего используется для изображения статистических данных. Информация такого графика является очень содержательной и полезной. Он одновременно отображает несколько величин, которые характеризуют вариационный ряд: минимальное и максимальное значение, среднюю и медиану, первый и третий квартиль.
4. Инструменты для считывания или создания матрицы. Для использования инструментов палитры необходимо иметь начальные данные в виде матрицы — одномерного массива. Его можно создать в документе с текущей сессией и в дальнейшем подставлять его название как входные данные в окнах инструментов палитры аналогично решению уравнений с помощью панели общих математических действий (General Math). Можно и непосредственно задавать в данные в окнах ввода входных данных. В этом случае они вводятся в принятом в системе виде, то есть в квадратных скобках и через запятую. Понятно, что первый вариант является значительно лучшим, поскольку он требует только одноразового введения данных.

Кроме панели, все статистические инструменты могут быть использованы также и с помощью соответствующих функций.