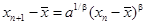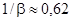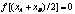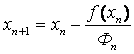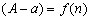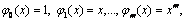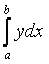Курсовая работа: Приближённые методы решения алгебраического уравнения
| Название: Приближённые методы решения алгебраического уравнения Раздел: Рефераты по математике Тип: курсовая работа Добавлен 02:58:05 24 марта 2008 Похожие работы Просмотров: 3709 Комментариев: 35 Оценило: 4 человек Средний балл: 3.5 Оценка: неизвестно Скачать | |||||||
 |
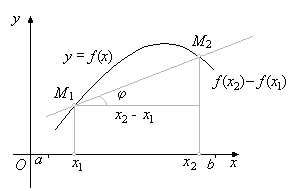
рис 2.3 геометрическая иллюстрация условия Липшица.
рис 3.3 геометрическая иллюстрация cвязи условия Липшица с предположением о дифференцируемости функции.
Предположим, что функция f(x) имеет на отрезке [a, b] ограниченную производную:
| f ¢(x)| £ m; тогда она удовлетворяет условию Липшица с постоянной a=m. Для доказательс- тва этого утверждения воспользуемся формулой конечных приращений Лагранжа:
где x1 , x2 , — произвольные точки отрезка [a, b] x, — некоторая точка отрезка [x1 , x2 ]. Возьмём модуль обеих частей равенства (4.3) и заменим в правой части | f ‘(x)| на m. В результате по- лучим неравенство (4.3) с a=m. Рис.2.3 даёт геометрическую иллюстрацию установленного свойства. Согласно формуле Лагранжа (5.3) каждой секущей графика функции y = f(x) мож- но поставить в соответствие параллельную её касательную. Поэтому наибольший тангенс угла наклона касательных, и его можно оценить той же константой m: |k| £ m.
Познакомившись с условием Липшица, перейдём к изучению итерационной последовательности, предполагая, что уравнение имеет корень x=c. Существование этого корня можно установить с помощью качественного предварительного исследования уравнения с применением теоремы о существовании корня непрерывной функции.
Теорема о существовании корня непрерывной функции
Если функция f(x) непрерывна на отрезке [a, b] и принимает на его концах значения разных знаков, то на этом отрезке существует, по крайней мере, один корень уравнения f(x).
Теорема о сходимости итерационной последовательности
Пусть с – корень уравнения (2.3) и пусть функция j(x) удовлетворяет на некотором отрезке [c-d, c+d] (d>0) условию Липшица с постоянной a 2 |x0 -c| £ a 2 d
Точка x2 опять принадлежит отрезку [c-d, c+d] и расположена ближе к точке c, чем точка x1 , т.е. мы приблизились к c.
По индукции легко доказать, что последующие итерации также существуют и удовлетворяют неравенствам.
Отсюда следует, что:

Остаётся доказать, что корень x=c (1.3) является единственным решением уравнения на отрезке [c-d, c+d]. Действительно, допустим, что существует ещё один корень x=c1 .
Примем c1 за нулевое приближение и будем строить итерационную последователь- ность (2.3). Тогда с учётом (7.3) получим xn =c1 (n=0, 1, 2, …). С другой стороны, по доказанному 
Сходимость итерационной последовательности к корню уравнения (1.3) может быть использована для приближённого определения корня с любой степенью точности. Для этого нужно только провести достаточное количество итераций.
4. Быстрота сходимости процесса итераций
Используем теперь производную функции j(x) для оценки скорости сходимости итераций при решении уравнения х=j(x). Нужно оценить скорость, с которой убывают погрешности an =x-xn приближённых значений х1 , … , хn , … корня x.
Можно заметить, что справедливы равенства x=j(x) и хn+ 1 =j(хn ). Из них вытекает, что:
Но по формуле Лагранжа имеем:
где cn — точка лежащая между точками x и хn . Поэтому:
Из равенства (1.4) вытекает следующий вывод:
Пусть x – корень уравнения x=j (x) — лежит на отрезке [a, b]. Если на этом отрезке выполняется неравенство |j ¢(x)| n ·|a1 | (2.4)
В самом деле, из равенства (1.4) имеем:
Но точка c1 лежит на отрезке [a, b] (рис.1.4), и потому:
Тем самым наше утверждение доказано.
Так само при 0 n ·|a1 |.
Точно так же можно доказать, что если на отрезке [a, b] выполнено неравенство:
то процесс итераций расходится.
Особенно быстро сходится процесс последовательных приближений, если в точке x производная функции j(x) обращается в нуль. В этом случае по мере приближения к x, значение j ¢(x) стремится к нулю. Так как:
то сходимость процесса ускоряется по мере приближения к точке x.
Однако то же самое можно наблюдать в методе Ньютона, при замене f(x)=0 на 


5. Метод касательных (метод Ньютона)
Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x):
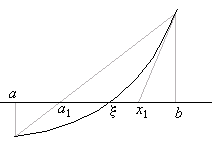
Графики функции f(x) и её касательной близки около точки касания, поэтому естественно ожидать, что точка x1 пересечения касательной с осью Ox будет расположена недалеко от корня c (рис. 1.5)
Для определения точки имеем уравнение:
Повторим проделанную процедуру: напишем уравнение касательной к графику функции f(x) при x=x1 и найдём для неё точку пересечения x2 с осью Ox (см. рис.1.5) x2 =x1 – f (x1 )/ f ¢(x1 ). Продолжая этот процесс, получим последовательность
Построение последовательности
При исследовании этой последовательности, как и последовательности метода итераций, встают два вопроса:
Можно ли процесс вычисления чисел xn продолжать неограниченно, т. е. будут ли числа xn принадлежать отрезку [a, b] ?
Если процесс (3.5) бесконечен, то как ведёт себя последовательность
При анализе этих вопросов предположим, что корень x=c является внутренней точкой отрезка [a, b] (a 0, | f ¢¢(x)|£M, xÎ[a, b], (4.5)
и докажем следующую теорему.
Теорема о сходимости метода касательных.
Если функция f(x) удовлетворяет условиям, сформулированным п.1., то найдётся такое d: 0 2 /(2M)
Тогда в силу (8.5) для данного e можно указать такое d: 0 ас, так как ас 2 — b — 1 = 0 (3.7)
Только положительный корень b квадратного уравнения (3.6) соответствует убыванию ошибки, т. е. сходящемуся процессу. Следовательно, в методе секущих

в то время как в методе Ньютона ошибка убывает быстрей (соответствуя b=2). Но в методе на каждой итерации надо вычислять и функцию, и производную, а в методе секущих – только функцию. Поэтому при одинаковом объёме вычисления в методе секущих можно сделать вдвое больше итераций и получить более высокую точность. Что является более приемлемым при численных расчётах на ЭВМ, чем метод касательных.
В знаменателе формулы (1.7) стоит разность значений функции. Вдали от корня это несущественно; но вблизи корня, особенно корня высокой кратности, значения функции малы и очень близки. Возникает потеря значащих цифр, приводящая к «разболтке» счёта. Это ограничивает точность, с которой можно найти корень; для простых корней это ограничение невелико. Приводить к общему знаменателю уравнение (1.7) не следует: может увеличится потеря точности в расчётах.
От «разболтки» страхуются так называемым приёмом Гарвика. Выбирают не очень малое e, ведут итерации до выполнения |xn + 1 -xn | 0, a f(x), a > x > b
В частности, если х0 корень уравнения (1.1): f(x0 ) = 0, отсюда следует, что
C (3.8) и (4.8) получаем:
поэтому из (5.8) следует x1 0, a 0,

Если случайно окажется, что точка а3 , вычисленная по формуле (1.9), лежит за пределами отрезка [a, b], то на следующем шаге надо вместо этой точки взять ближайший к ней конец этого отрезка (рис. 1.9, б). Оказывается, что сходимость усовершенствованного метода хорд гораздо быстрее, чем у обычного. Именно, если x — корень уравнения f(x)=0, то:
|an + 1 | S , где
10. Комбинированный метод решения уравнений
При решении уравнений часто комбинируют методы хорд и Ньютона. Если график функции y=f(x) обращён вогнутостью вверх, то находят точки а1 и х1 по формулам:


Если же график функции y=f(x) обращён вогнутостью вниз, то точку а1 находят по формуле (1.10), а точку х1 – по формуле:

Как видно из рис.1.10 а) и б), корень x уравнения f(x)=0 лежит обычно между полученными точками а1 и х1 . Применяя снова к этим точкам формулы метода хорд и метода Ньютона, получают новую пару точек а2 и х2 и т. д.
Таким путём получают две последовательности точек а1 , а2 , а3 , …, an , … и x1 , x2 , x3 , … , xn , …, приближаются с разных сторон к искомому корню x. Преимущество описанного метода состоит в том, что при нём получаются приближённые значения как с избытком так и с достатком.
11. Заключительные замечания
Ситуация, когда одну и ту же задачу можно решить многими способами, является довольно типичной. В таких случаях естественно возникает необходимость сравнения их между собой.
При оценке эффективности численных методов существенное значение имеют различные свойства:
простота организации вычислительного процесса и контроля над точностью;
Наиболее универсальным является метод деления пополам (дихотомии): он только требует непрерывности функции. Остальные методы накладывают более сильные ограничения. Во многих случаях это преимущество метода вилки может оказаться существенным.
С точки зрения организации вычислительного процесса все виды численного нахождения корней уравнения очень просты. Однако и здесь метод деления пополам обладает некоторым преимуществом. Вычисления можно начинать с любого отрезка [a, b], на концах которого непрерывная функция f(x) принимает значения разных знаков. Процесс будет сходится к корню уравнения f(x)=0, причём на каждом шаге он даёт для корня двустороннюю оценку, по которой легко определить достигнутую точность. Сходимость же метода итераций или касательных зависит от того, насколько удачно выбрано нулевое приближение.
Исследование методов приближенного решения уравнений
Работа посвящена исследованию методов приближенного решения уравнений. Рассмотрены следующие методы приближенногорешения уравнений: метод половинного деления, метод хорд, метод касательных, комбинированный метод, построены компьютерные модели всех изученных методов на языке программирования Free Pascal. Модели позволили провести сравнительный анализ изученных методов и выбрать среди них оптимальный.
Скачать:
| Вложение | Размер |
|---|---|
| start_v_nauku.docx | 161.16 КБ |
Предварительный просмотр:
Городская научно – практическая конференция
Исследование методов приближенного решения уравнений
Секция: современное программирование
Автор: Сергеева Мария Сергеевна,
11 «Б» класс, МБОУ «Средняя общеобразовательная школа № 27»
Руководитель: Сергеева Светлана Александровна
Учитель информатики 1 категории,
МБОУ «Средняя общеобразовательная школа № 27»
- Теоретическая часть 4
- Метод половинного деления 5
- Метод хорд 7
- Метод касательных 8
- Комбинированный метод хорд и касательных 9
- Практическая часть 11
- Компьютерная модель построения графика функции на языке программирования Free Pascal 11
- Компьютерная модель метода половинного деления 13
- Компьютерная модель метода хорд 14
- Компьютерная модель метода касательных 15
- Компьютерная модель комбинированного метода хорд и касательных 16
- Сравнительный анализ методов 17
С термином «уравнение» мы знакомимся еще в начальной школе, а задача «решить уравнение», вероятно, является наиболее часто встречающейся задачей не только на уроках математики.
На уроке алгебры при решении уравнений возникают ситуации, когда путем алгебраических преобразований уравнение решить невозможно. Для решения данной проблемы, существуют методы приближенного решения уравнений.
Актуальность темы обоснована тем, что с развитием компьютерной техники методы решения уравнений, основанные на большом количестве повторов, получают возможность широкого применения.
Цель : нахождение оптимального метода приближенного решения уравнения.
- Изучить методы приближенного решения уравнения:
- метод половинного деления
- метод хорд
- метод касательных
- комбинированный метод
- Создать компьютерные модели приближенного решения уравнений с помощью всех методов на языке программирования Free Pascal.
- Провести сравнительный анализ методов.
Нелинейные уравнения можно разделить на 2 класса — алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.) называются трансцендентными.
Методы решения нелинейных уравнений делятся на две группы:
- точные методы;
- итерационные методы (за счет последовательных приближений получить решение уравнения с необходимой точностью).
Точные методы решения уравнений основываются на поиске равносильных преобразований алгебраических выражений, например, перенос слагаемых из одной части уравнения в другую с противоположным знаком, деление обеих частей уравнения на одинаковое число не равное 0, а также точные способы решений позволяют записать корни уравнения в виде некоторого конечного соотношения (формулы). Точные решения существуют только для некоторых уравнений определенного вида (линейные, квадратные, тригонометрические и др.), поэтому для большинства уравнений приходится использовать методы приближенного решения с заданной точностью (графические или численные). В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение выше четвертой степени.
Точные методы решения Приближенные методы решения
Например, уравнение x3+cos x=0 нельзя решить путем равносильных алгебраических преобразований. Но это уравнение можно решать приближенно графическими и численными методами.
Решение уравнения проводят численно в два этапа. На первом этапе производится отделение корней — поиск интервалов, на которых содержится только по одному корню. Второй этап решения связан с уточнением корня на выбранном интервале (определением значения корня с заданной точностью). Далее будут рассмотрены несколько численных методов и приведены алгоритмы нахождения корней уравнений.
Отделение корней уравнения может проводиться графически, т.е. путем построения графика функции y=f(x). Для уравнения вида f (x) = 0 , где f(x) – некоторая непрерывная функция, корень (или корни) этого уравнения являются точкой (или точками) пересечения графика функции с осью абсцисс.
Решение уравнений с заданной точностью
Метод половинного деления
f(x)=0,
где f(x) — непрерывная функция
Отделение корней уравнения можно осуществить путем построения компьютерных моделей:
- построение графика функции с помощью одного из языков программирования (в данном случае Free Pascal);
- построение графика функции в электронных таблицах Microsoft Excel путем построения диаграммы типа График .
При построении графика функции корни уравнения можно получить лишь с небольшой степенью точности. Поэтому, чтобы эти значения получить с любой заданной степенью точности, необходимо применять методы, которые позволяют «уточнять» найденные значения.
Рассмотрим методы уточнения корней и их основные идеи. Отметим следующий момент: при прочих равных условиях, тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден за меньшее число раз вычисления функции f(x).
1.1. Метод половинного деления
Самый простой из них – метод половинного деления, или иначе метод дихотомии. Метод дихотомии получил свое название от древнегреческого слова διχοτομία, что в переводе означает деление надвое. Его мы используем довольно часто. Допустим, играя в игру «Угадай число», где один игрок загадывает число от 1 до 100, а другой пытается его отгадать, руководствуясь подсказками «больше» или «меньше». Логично предположить, что первым числом будет названо 50, а вторым, в случае если оно меньше — 25, если больше — 75. Таким образом, на каждом этапе неопределенность неизвестного уменьшается в 2 раза. Т.е. даже самый невезучий в мире человек отгадает загаданное число в данном диапазоне за 7 предположений вместо 100 случайных утверждений.
Алгоритм метода половинного деления основан на теореме Больцано — Коши о промежуточных значениях непрерывной функции и следствии из неё.
Теорема Больцано — Коши: если непрерывная функция принимает два значения, то она принимает любое значение между ними.
Следствие (теорема о нуле непрерывной функции): если непрерывная функция принимает на концах отрезка положительное и отрицательное значения, то существует точка, в которой она равна 0.
Приближенные методы решения конечных уравнений
1. Погрешность результата численного решения задачи. Источники погрешности. Абсолютная и относительная погрешность.
Число а называют приближенным, если оно мало отличается от точного числа А и заменяет его в вычислениях. Приближенные числа удобно представлять в виде десятичной дроби, оценивая их значения по числу значащих цифр.
Значащими именуют цифры приближенного числа, начиная с пер вой, отличной от нуля, слева, и кончая последней, за точность которой можно поручиться.
Например, числа 34,537, 0,00362 и 7,002 имеют пять, три и четыре значащих цифры соответственно.
Точные числа А могут иметь цифр больше, чем это необходимо. В этих случаях точные числа заменяют приближенными, пользуясь пра вилом их округления. Округлить число до заданного разряда или до требуемого количе ства значащих цифр означает сохранить требуемое количество цифр (отсчитывается слева) при отбрасывании остальных.
Например, 6,426281 = 6,43 означает округление до сотых или до трех значащих цифр.
При округлении числа стремятся получить минимальную погрешность, руководствуясь следующим правилом: если первая из отбрасываемых цифр меньше 5, то все последующие цифры зачеркивают, если же она больше или равна 5 (см. пример выше), то отбрасываемые циф ры заменяют единицей более высокого разряда.
Разность между точным значением числа А и его приближенным значением 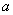

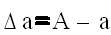
Как видно из (1.1), погрешность 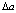
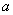
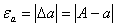
Поскольку точное значение числа А обычно неизвестно, то неиз вестна и абсолютная погрешность 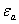
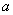
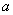
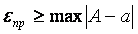
Заметим, что 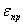
Абсолютная погрешность 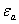
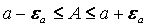
2. Методы решения конечных уравнений
Пусть имеем уравнение
на заданном сегменте [а, b]. Предположим также, что функция f(x) кусочно-непрерывна и имеет кусочно-непрерывную производную.
Функцию (4.20) называют алгебраическим уравнением n-й степени, если f(х) можно представить соответствующим полиномом, т.е.
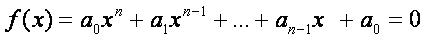
Если же в f ( x ) входят элементарные (тригонометрические, показатель ные, логарифмические и т.п.) функции, то имеем трансцендентное уравнение.
Алгебраические и трансцендентные уравнения обобщают термином «конечные» уравнения.
Всякое значение х = £, обращающее функцию (1.20) в нуль, т.е. такое, что f(£) = 0, называют корнем уравнения f ( x ) = 0. Способ опре деления указанного корня именуют решением уравнения. Некоторые из корней уравнения (1.20) могут совпадать (повторяться). В этом случае имеют кратные корни. При k совпадающих корнях имеют корень k -й кратности. Если k = 1, то имеют простой корень. Число £ является кор нем k -й кратности, если при x : = £ обращаются в нуль как функция f(£) , так и все ее производные до (k-1)-го порядка включительно:
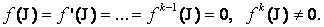
Численное решение конечных уравнений (приближенное определе ние значений корней) удобно проводить по следующей методике. Сначала выявляют достаточно малые промежутки для каждого из корней (простого или кратного) уравнения, т.е. выполняют процедуру отделения корней. Затем находят в этих промежутках значения корней с заданной точностью, обеспечивая тем самым уточнение корней. Отделение корней можно проводить графически и аналитически.
При графическом способе исходное уравнение (1.20) представляют в форме
получая два графика:
Поскольку для корней уравнения (1.20)
то их численные значения получают по абсциссам точек пересечения этих графиков. В частном случае при f2(х) = 0 график функции у2 = f2(х)=0 совпадает с осью абсцисс и тогда искомые корни конечного уравнения (1.20) получают по точкам пересечения графика f(х) = f1(х) с этой осью.
Аналитические методы отделения корней конечных уравнений используют различные способы упрощенного аналитического решения задачи. Наибольший практический интерес имеют две следующие разновидности. В первой осуществляется переход от искомого к более простому уравнению, имеющему приблизительно те же самые значения корней. Зачастую это достигается исключением из исходного уравне ния членов с малыми значениями коэффициентов. Вторая разновид ность основана на непосредственном применении свойств непрерывных функций (известных теорем) для конкретизации различных вспомога тельных процедур: определения числа корней для алгебраических урав нений, анализа промежутков с корнями, косвенного нахождения некото рых корней и т.п.
Что же касается процедуры уточнения корней, то она проводится как при графических, так и при аналитических способах по единой методике, заключающейся в оценке точности найденных корней (для действительных значений) посредством неравенств
где ak и bk — начало и конец интервала, в котором располагается k -й корень £ k функции f( x ) .
Тогда в качестве первого приближенного значения для k-го корня можно принять, например, центр интервала
В этом случае для абсолютной погрешности 8и (см. разд. 4.3) имеем
При необходимости получить более высокую точность удобно применять итерационные методы, заключающиеся в следующем. Подставляют приближенное значение k -го корня (1.27) в исходное уравнение (1.20) и, принимая f (£ k 1 ) = bk 1 или f (£ k 1 ) = ak 1 , находят второе значение этого корня в более узком интервале
Повторяя эту процедуру многократно, можно выполнить уточнение корня с любой заданной точностью
3. Метод половинного деления
Если вид исходной функции f (х) достаточно сложный, то вычисление f ‘( x ) в методе касательных может заметно усложнить алгоритм 1.2.
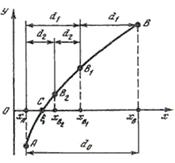
Для решения таких уравнений на ЭВМ особенно удобен метод половинного деления. В этом методе также требуется, чтобы ординаты анализируемой функции f ( x ) =0 имели на границах сегмента [ хA , хB] разные знаки (рис. 1.7),
Для нахождения корня, принадлежащего промежутку
( хB1 — хA ) . делим его пополам, исследуя исходную функцию в средней точке х = хB1 . Здесь возможны следующие случаи:
совпадение значения корня х = x с абсциссой точки хB1 , т.е.
откуда искомый корень
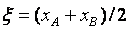
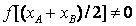
В этом варианте нужно выбрать ту из половин промежутка, н a концах которой фунция f(х) имеет противоположные знаки, т.е. где . выполняется условие (1.45).
На рис. 1.7 этому условию удовлетворяет промежуток
Продолжая указанную про цедуру половинного деления, по лучаем в общем случае бес конечную последовательность вложенных один в другой отрез ков
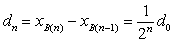
В пределе при 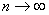
соотно шение (1.48) имеет общий предел, совпадающий со значением корня х = x . Тогда абсолютная точность расчета корня методом половинного деления
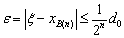
Метод половинного деления отли чается несколько худшей сходимо стью, чем метод касательных, и поэтому требует больших вычислени й. Однако он в отличие от метода хорд легко реализуем на ЭВМ.
Сущность метода также основана на последовательном приближении к искомому корню конечного уравнения
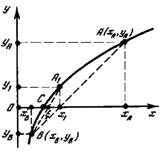
f (х) = 0. Однако в отличие от метода касательных здесь на каждом шаге итерационного процесса участок истинной кривой у = f ( x ) заменяют соответствующей хордой.
 |
Расчетная формула.
На рис. 1.6 показан график функции у = f ( x ) вблизи корня x , которому соответствует точка пересечения дуги ВА с осью абсцисс.
Задавая два значения хA и хB, которым соответствуют разные знаки фунции f ( x ), например:
соединяют эти точки хордой ВА.
Уравнение прямой ВА можно записать
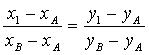
При y 1 = 0 получаем значение точки пересечения х1 этой прямой (хорды) с осью абсцисс, т.е.
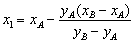
Откуда после несложных пре образований получают
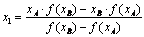
Выявив знак функции f ( x 1 ) в най денной точке х1 (см. рис. 1.6), заменяют соответствующее по знаку значе нение х A или хB в (1.41) новой более точной величиной х1. Так, например, для случая, анализируемого на рис. 1.6 , в (1.40) требуется заменить х A значением х1, получая уже для хор ды BА1 второе приближение корня
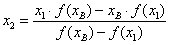
Продолжая эту процедуру, получают для (n+1)-го приближения
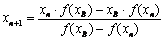
Как видно из рис. 1.6, сходящаяся последовательность значений x k ( k = 1, 2, . n+1) обеспечивает получение корня xk = x с любой точ ностью.
При разработке машинных алгорит мов расчетное соотношение (1.42) преобразуют к более удобному для итерационных формул виду, т.е.
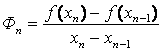
В этом случае условие сходимости решения можно записать
5. Метод касательных
Метод касательных широко используют при машинных способах уточнения корней алгебраических и трансцендентных уравнений из-за удобства обеспечения итерационного процесса и хорошей сходимости решения.
При выделении интервала (а, b), в котором ищется действительный корень уравнения,
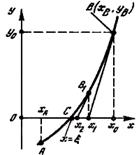 |
исходят из следующего предположения. Если на границах некоторого интервала непрерывная функция f(х) принимает значения разных знаков, то в этом интервале уравнение f(х) = 0 имеет хотя бы один корень.
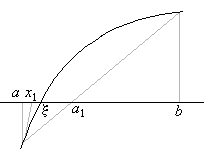
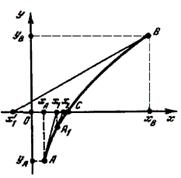
Сущность метода заключается в последовательном приближении к искомому корню конечного уравнения f(х) = 0 за счет взаимосвязанного смещения соответствующих касательных. Для уяснения метода на рис. 1.4 показан график функции y = f ( x ), пересекающей ось Ох в точке С, абсцисса которой х = x является корнем уравнения f(х) = 0 .
Пусть АВ (см. рис. 1.4) — дуга кривой у = f (х) вблизи корня и обращена выпуклостью к оси Ох. Проведем через точку В с координатами (хв, ув) касательную к кривой. В этом случае угловой коэффициент касательной будет равняться производной от функции f (х) в точке касания В:
Тогда уравнение этой касательной, т.е. прямой Bx 1 , можно записать как
где х1 — абсцисса точки пересечения касательной с осью.
Полагая xB = х0 и решая (1.32) относительно х1, получаем первое приближение для корня
Абсциссе x 1 будет соответствовать новое значение функции у1= f ( x 1 ), определяемое координатами точки В1. Проводя касательную из точки В1 и повторяя многократно описанную процедуру, получаем итерационную формулу Ньютона
Она позволяет шаг за шагом находить более точные значения простых корней алгебраических или трансцендентных уравнений f ( x ) = 0. При этом величины x0, xt x 2 . образуют сходящуюся к иско мому корню х = x последовательность (см. рис. 1.4).
 |
Заметим, что при использовании фор мулы Ньютона может иметь место недопустимый процесс расхождения решения. Например, на рис. 1.5 представлен график функции у = f ( x ), обращенной к оси Ох вогнутостью.
Пусть по аналогии с предыдущим случаем (см. рис. 1.4) здесь также исходной является точка В. Нетруд но заметить, что касательная Вх1’ не может обеспечить решения за дачи. В то же время, если выбрать за исходную точку А, получим сходящуюся последовательность значений xA , х1, х2,….
Для проверки правильности выбора начального значения х0 , обес печивающего схождение вычислительного процесса, следует руковод ствоваться соотношением
где f ’’( x 0 ) — вторая производная анализируемой функции в выбранной исходной точке х0 .
Таким образом, простой корень алгебраических или трансцендентны x уравнений f ( x ) = 0 можно вычислить по формуле Ньютона (1.33) с любой сколь угодной точностью, если нулевое приближение х0 взято настолько близко к корню х = x , что в интервале ( x , х0 ):
а) наклон кривой у = f ( x ) не равняется нулю.т.е.
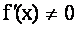
б) кривая у = f ( x ) не имеет точек перегиба, т.е.
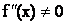
Для расчета корней с точностью до e итерационный процесс следу ет прекратить при выполнении условия
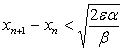
где a — наименьшее значение f ‘( x ) на сегменте [ xA , xB ]; b — наи большее значение | f «( x )| на этом же сегменте. Условию (1.35) будет отвечать неравенство
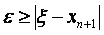
По формуле Ньютона можно находить и кратные корни, если использовать (4.36), но уже для производной от функции f ( x ), т.е. в общем случае
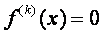
•где k =1, 2. — порядок кратности корня для уравнения (1.20).
6. Метод простой итерации для решения конечных уравнений
Пусть имеем уравнение
на заданном сегменте [а, b]. Предположим также, что функция f(x) кусочно-непрерывна и имеет кусочно-непрерывную производную.
Функцию (4.20) называют алгебраическим уравнением n-й степени, если f(х) можно представить соответствующим полиномом, т.е.
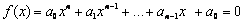
Если же в f ( x ) входят элементарные (тригонометрические, показатель ные, логарифмические и т.п.) функции, то имеем трансцендентное уравнение.
Алгебраические и трансцендентные уравнения обобщают термином «конечные» уравнения.
Всякое значение х = £, обращающее функцию (1.20) в нуль, т.е. такое, что f(£) = 0, называют корнем уравнения f ( x ) = 0. Способ опре деления указанного корня именуют решением уравнения. Некоторые из корней уравнения (1.20) могут совпадать (повторяться). В этом случае имеют кратные корни. При k совпадающих корнях имеют корень k -й кратности. Если k = 1, то имеют простой корень. Число £ является кор нем k -й кратности, если при x : = £ обращаются в нуль как функция f(£) , так и все ее производные до (k-1)-го порядка включительно:
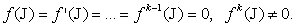
Численное решение конечных уравнений (приближенное определе ние значений корней) удобно проводить по следующей методике. Сначала выявляют достаточно малые промежутки для каждого из корней (простого или кратного) уравнения, т.е. выполняют процедуру отделения корней. Затем находят в этих промежутках значения корней с заданной точностью, обеспечивая тем самым уточнение корней. Отделение корней можно проводить графически и аналитически.
При графическом способе исходное уравнение (1.20) представляют в форме
получая два графика:
Поскольку для корней уравнения (1.20)
то их численные значения получают по абсциссам точек пересечения этих графиков. В частном случае при f2(х) = 0 график функции у2 = f2(х)=0 совпадает с осью абсцисс и тогда искомые корни конечного уравнения (1.20) получают по точкам пересечения графика f(х) = f1(х) с этой осью.
Аналитические методы отделения корней конечных уравнений используют различные способы упрощенного аналитического решения задачи. Наибольший практический интерес имеют две следующие разновидности. В первой осуществляется переход от искомого к более простому уравнению, имеющему приблизительно те же самые значения корней. Зачастую это достигается исключением из исходного уравне ния членов с малыми значениями коэффициентов. Вторая разновид ность основана на непосредственном применении свойств непрерывных функций (известных теорем) для конкретизации различных вспомога тельных процедур: определения числа корней для алгебраических урав нений, анализа промежутков с корнями, косвенного нахождения некото рых корней и т.п.
Что же касается процедуры уточнения корней, то она проводится как при графических, так и при аналитических способах по единой методике, заключающейся в оценке точности найденных корней (для действительных значений) посредством неравенств
где ak и bk — начало и конец интервала, в котором располагается k -й корень £ k функции f( x ) .
Тогда в качестве первого приближенного значения для k-го корня можно принять, например, центр интервала
В этом случае для абсолютной погрешности 8и (см. разд. 4.3) имеем
При необходимости получить более высокую точность удобно применять итерационные методы, заключающиеся в следующем. Подставляют приближенное значение k -го корня (1.27) в исходное уравнение (1.20) и, принимая f (£ k 1 ) = bk 1 или f (£ k 1 ) = ak 1 , находят второе значение этого корня в более узком интервале
8. Общая формулировка задачи приближения функций
Введем понятие обобщенного многочлена:
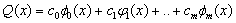
где f k (х) , k = 0, 1, 2, . m — система непрерывно дифференцируемых функций; ck , k = 0,1. т — постоянные коэффициенты.
Задача о приближении формулируется следующим образом: данную функцию f ( x ) требуется приближенно заменить (аппроксимировать) обобщенным полиномом Q ( x ) так, чтобы отклонение f ( x ) от Q ( x ) на заданном множестве Х = было наименьшим. Это можно достичь надлежащим подбором коэффициентов (2.7). Тогда многочлен Q ( x ) называют аппроксимирующим.
Если множество Х состоит из отдельных точек, то имеют точечное приближение, если же Х является отрезком
a £ х £ b , то получают интегральное приближение.
На практике используют систему функций < f k (х) > с целыми неотрицательными степенями переменной х, т.е.
тогда функция Q ( x ) отображается обычным многочленом:
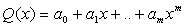
9. Интерполяционная формула Лагранжа.
Полагая т= п, можно найти коэффициенты
а i , i = 0, 1, 2, . п интерполяционного многочлена Q ( x ) системы уравнений
которая имеет единственное решение. Заметим, что в правой части система (2.10) имеет значения заданной функции f ( x ) в узлах интерполяции, т.е. у i = f ( x ).
Многочлен Q ( x ) = Ln ( x ), коэффициенты которого находят из решения (2.10), называют интерполяционной формулой Лагранжа:

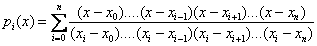
Если функция f ( x ), подлежащая интерполяции, достаточное число раз дифференцируема, то погрешность интерполяции можно рассчитать по формуле
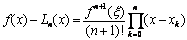
где x , — некоторое число в интервале интерполяции и зависящее от x .
10. Численное интегрирование Формула Ньютона-Котеса
Пусть для заданной функции требуется вычислить определенный интеграл
1. Выбираем шаг h = ( b — а)/п и разбиваем сегмент [а, b ] на п равных частей посредством равноотстоящих точек
2. Заменяем функцию у соответствующим интерполяционным многочленом Ln ( x ) Лагранжа (см. разд. 2.3) и получаем
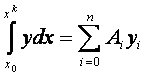
где А i , — некоторые коэффициенты.
3. Обращаясь к (2.11), с учетом обозначений
Интерполяционный многочлен Лагранжа можно записать
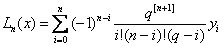
4. Подставив полученное значение Ln ( x ) в (2.38) вместо у и выполнив замену переменных в интеграле, имеем
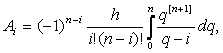
Тогда для коэффициентов Котеса Hi , получаем
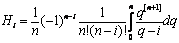
6. Формулу Ньютона-Котеса можно в этом случае представить так:
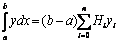
http://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2012/02/09/issledovanie-metodov-priblizhennogo-resheniya
http://pedstudent.narod.ru/chis_m/otv1.htm



 . Согласно неравенству (2.1) пределы с1 и с2 удовлетворяют неравенству с1 £ с2 . Итак, an £ с1 0, то чтобы её достигнуть достаточно сделать число шагов N, не превышающее log2 [(b-a)/e]: N>log2 [(b-a)/e].
. Согласно неравенству (2.1) пределы с1 и с2 удовлетворяют неравенству с1 £ с2 . Итак, an £ с1 0, то чтобы её достигнуть достаточно сделать число шагов N, не превышающее log2 [(b-a)/e]: N>log2 [(b-a)/e]. , c=j(c) (3.3)
, c=j(c) (3.3) , что означает непрерывность функции f(x).
, что означает непрерывность функции f(x).