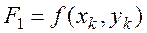Приближенные методы решения линейных уравнений

Итерационные методы решения системы линейных алгебраических уравнений

В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.

Общие сведения об итерационных методах или методе простой итерации

Метод итерации — это численный и приближенный метод решения СЛАУ.

Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .

Рассмотрим систему A x = b .

Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.

Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.

Метод Якоби

Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.

Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:

b i j = — a i j / a i i , i , j = 1 , 2 . . . , n

Элементы (компоненты) вектора d вычисляются по следующей формуле:

d i = b i / a i i , i = 1 , 2 , . . . , n

Расчетная формула метода простой итерации:

x ( n + 1 ) = B x ( x ) + d

Матричная запись (координатная):

x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b

Критерий окончания в методе Якоби:

x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε

В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:

x ( n + 1 ) — x ( n ) ε

Решить СЛАУ методом Якоби:

10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10

Необходимо решить систему с показателем точности ε = 10 — 3 .

Приводим СЛАУ к удобному виду для итерации:

x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1

Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.

В таком случае, первая итерация имеет следующий внешний вид:

x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01

Аналогичным способом вычисляются приближения к решению:

x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111

Находим норму матрицы В , для этого используем норму B ∞ .

Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:

x ( n + 1 ) — x ( n ) ε

Далее вычисляем нормы разности векторов:

x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .

Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.

x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .

Метод Зейделя

Метод Зейделя — метод является модификацией метода Якоби.

Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.

x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +

+ . . . + b i m x m ( n ) + d i

За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.

Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.

Решим 3 системы уравнений:

2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1

Приведем системы к удобному для итерации виду:

x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .

Отличительная особенность, условие сходимости выполнено только для первой системы:

Вычисляем 3 первых приближения к каждому решению:

1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109

Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.

2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129

Итерационный процесс разошелся.

Решение: x 1 = 1 , x 2 = 2

3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2

Итерационный процесс зациклился.

Решение: x 1 = 1 , x 1 = 2

Метод простой итерации

Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:

x = x — τ ( A x — b ) , τ — итерационный параметр.

Расчетная формула имеет следующий внешний вид:

x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .

Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .

Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .

τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .

Приближённые методы решения СЛАУ

Лекция 1

Приближённые методы решения СЛАУ

А) Метод простых итераций.(Метод последовательных приближений).

Пусть дана система n линейных уравнений с n неизвестными:

(1)

или где — заданные числа; .

Задаются произвольно n-чисел – нулевое приближение искомой функции.

Далее подставляем в правую часть системы (1) нулевое приближение и

находим первое приближение.

, (2)

Затем по 1-ому приближению находят 2-ое, 3-е и т.д.

В результате для k-ого приближения получаем формулу:

, (2’)

Таким образом мы получили последовательность векторов

Х (0) ,Х (1) ,…, Х (К) , к=1,2,…

Если любая из таких последовательностей <Х_i (к) > сходится некоторому пределу x_i k = c_i , ,то данный вектор с_i, является решением сист. (1)

В равенстве (2’) перейдем к пределу при k→∞ при замене х_i на с_i.

Теорема(достаточные условия сходимости простой итерации):

Пусть выполняется хотя бы одно из следующих условий (нормы матрицы):

а) Если максимум суммы модулей коэффициентов при неизвестных (по строкам) меньше 1:

б) Если максимум суммы модулей коэффициентов при неизвестных (по столбцам) меньше 1:

в) Если сумма всех элементов в квадрате меньше 1.

Если выполняется хотя бы одно, тогда справедливы утверждения:

1)система (1) имеет единственное решение (С₁. С_n);

2)последовательность , где i = определяется по формуле (2), при любом начальном приближении сходится к соответствующим компонентам точного решения. i =

3)для приближенного равенства верны оценки (x₁ ( k ) ,…x_n ( k ) ) 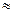(C_1,…C_n),

а’) есливыполняется условие а), то

б’) если выполняется условие б), то

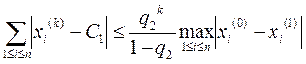
в’) если выполняется условие в), то

Замечания:

1)Если нет никакой информации о точном решении СЛАУ, то за начальное приближение выбираем столбец свободных коэффициентов. (из приведенной матрицы);

2)остановка вычислений производной по заданной величине абсолютной погрешности и приведенным в теореме оценкам.

Б) Метод Зейделя.

Этот метод является модификацией МПИ и заключается в том, что при вычислении (к+1) приближения неизвестного х_i (i>1), используются уже вычисленные ранее (к+1) приближения неизвестных х₁, х₂,…, х_i_-1

Рассмотрим систему: 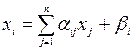i=1,n

Пусть матрица α удовлетворяет одному из условий теоремы:

Если, а) j. Аналогично, матрица называется нижнетреугольной, если все элементы выше главной диагонали (i

Прямой ход.

Это основной этап решения системы уравнений с помощью метода Гаусса. Его суть состоит в приведении исходной расширенной матрицы системы к верхнетреугольной матрице с помощью эквивалентных преобразований (добавление к строке любой линейной комбинации других строк и перестановка строк, т.е. уравнений). Формулы прямого хода соответствуют последовательному выражению переменных из уравнений и подстановке их в последующие уравнения, т.е. их фактическому исключению из последующих уравнений системы. При этом шагом считается исключение одной переменной из всех последующих уравнений системы.

Рассмотрим k-ый шаг прямого хода. На k-ом шаге матрица системы имеет вид:

Осталось n-k+1 неизвестных. Чтобы удалить х(k) из последней строчки, например, надо из нее вычесть k-ую строчку с таким коэффициентом, чтобы получить на месте а_nk ноль. Для этого коэффициент должен быть равен c_nk=a_nk/a_kk. Элемент а_kk называется разрешающим элементом k-ого шага и должен быть отличен от 0.

Формулы прямого хода

c_mk=a_mk/a_kk где 1

,откуда получаем:

Лекция 2.

Выбор шага

1. Пусть требуется вычислить интеграл с точностью ε. Используя формулу соответствующего остаточного члена R, выбирают h таким образом, чтобы выполнялось неравенство .

2. Двойной пересчёт. ( Правило Рунге).

Лекция 4

ЧИСЛЕННОЕ РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ И НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

Если алгебраическое или трансцендентное уравнение достаточно сложное, то его корни сравнительно редко удаётся найти точно. Поэтому большое значение приобретают способы приближённого нахождения корней уравнения и оценки степени их точности.

Процесс нахождения приближённых значений корней уравнения:

f(x) = 0, (1)

где функция f(x) определена и непрерывна в некотором конечном или

бесконечном интервале a n раз. Таким образом, число итераций n в данном методе зависит от предварительно заданной точности ε и от длины исходного отрезка и не зависит от вида функции f(x). Это является важным преимуществом метода половинного деления по сравнению с другими методами. Метод, однако, медленно сходится при задании высокой точности расчёта.

Метод хорд.

Пусть на отрезке [a,b] функция f(x) непрерывна и принимает на концах отрезка значения разных знаков, а производные f ′(x) и f ″(x) сохраняют постоянный знак на интервале (a,b). Тогда возможны четыре случая расположения дуги кривой (рис.4).

Рис.4.

В методе хорд за очередное приближение берём точку пересечения с осью Х прямой (рис.5), соединяющей точки (a,f(a)) и (b,f(b))

Причём одна из этих точек фиксируется − та, для которой знаки f(x) и f ″(x) одинаковы.

Для рис.5 неподвижным концом хорды является х =a.

Уравнение хорды АВ:

Точка пересечения хорды с осью Х (у=0): .

Теперь корень находится на отрезке [a,c₁]. Заменяем b на с₁.

Рис.5. Иллюстрация метода хорд.

Применяя метод хорд к этому отрезку, получим:

Продолжим и т.д., получим: (2) Условие окончания вычислений:

│с_n₊₁ − c_n│ 0, то приближённое значение корня находят по формуле (2), если f′(x)∙f″(x) ( n ) ) = 0 или .

Определение: Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

у′-2ху 3 +5=0—— уравнение первого порядка,

у″+ky′-by-sinx=0—— уравнение второго порядка.

Задача Коши (для уравнения первого порядка):

у′ = f(x, y) (1) найти решение y = y(x),

удовлетворяющее начальному условию: у(х₀)=у₀. (1*).

Т.е. найти интегральную кривую, проходящую через точку М(х₀, у₀).

Если f(x,y) непрерывна в области R: |x-x₀| ( n ) =f(x,y,y′,…,y ( n -1) ) задача Коши состоит в нахождении решения у = у(х), удовлетворяющего начальным условиям:

у(х₀) = у₀, у′(х₀) = у′₀, …, у ( n -1) (x₀) = y ( n -1) ₀ ― заданные числа.

Функция у = f(x, C₁, C₂,…, C_n), где С₁,…, С_n― произвольные постоянные, называется общим решением ОДУ или общим интегралом.

Эти постоянные можно определить с помощью начальных условий. Решение ДУ при заданных начальных условиях называется его частным решением.

Определение: задача называется краевой, если указывается интервал интегрирования [a,b] и ставятся дополнительные условия для значений функции у и её производных на концах этого интервала.

Процесс познания закономерностей и стремление создать детальную картину исследуемых явлений приводит к более сложной количественной оценке, отражающей эти явления, а именно к функции многих переменных, зависящих как от пространственных координат, так и от времени u = f(x₁, x₂,…, x_n, t).

Определение: Дифференциальным уравнением с частными производными называется уравнение, связывающее независимую переменные х₁, х₂, …, х_n, t, искомую функцию

u = f (х₁, х₂, …, х_n, t) и её частные производные:

Постановка задачи.

Дано дифференциальное уравнение первого порядка: у′ = f(x,y) (1).

Требуется найти решение этого уравнения на отрезке [x₀, x_max], удовлетворяющее начальным условиям: у(х₀) = у₀ (2).

В вычислительной практике более предпочтительным являются численные методы нахождения приближённого решения в фиксированных точках: х₀ 1 и b₀ = 0 ― явными многошаговыми.

― при r > 1 и b₀ ≠ 0 ― неявными многошаговыми.

Многошаговость нарушает однородность вычислительного процесса, используя для получения недостающей информации другие вычислительные схемы ( например, одношаговые).

А) Метод Эйлера.

х	x₀	x₁	…	х_n
y	y₀	y₁	…	y_n

Для решение Д.У.(1) с Н.У. (2) на отрезке [x₀, x_max] по методу Эйлера, таблица приближённых значений у(х) для равноотстоящих узлов:

Абсолютная погрешность формулы (4) на каждом шаге имеет порядок h 2

(5)

Формула (4) означает, что на отрезке [x_k, x_k₊₁] интегральная кривая y = y(x) приближённо заменяется прямолинейным отрезком, выходящим из точки М(х_k;у_k) с угловым коэффициентом f(х_k;у_k). В качестве приближения искомой интегральной кривой получаем ломаную линию с вершинами в точках М₀(х₀;у₀), М₁(х₁;у₁),…, М_n(х_n;у_n). Первое звено касается истинной интегральной кривой в точке М₀(х₀;у₀).

Метод Эйлера может быть применён к решению системы ОДУ и ДУ высших порядков. Последние должны быть предварительно приведены к системе ОДУ первого порядка.

Пусть задана система ОДУ первого порядка: (6)

Приближённые значения у(х_i) ≈ y_i_, z(х_i) ≈ z_i вычисляются по формулам:

(8)

Метод Эйлера обладает двумя существенными недостатками:

1) малой точностью (метод первого порядка точности);

2) систематическое накопление ошибок.

В) Модификации метода Эйлера.

1 ый усовершенствованный метод Эйлера.

Сначала вычисляют промежуточные значения:

(9)

А затем полагают: (10)

2 o й усовершенствованный метод Эйлера.

Сначала определяют «грубые приближения»: (11)

И приближённо полагают: (12)

Локальная погрешность на i-ом шаге: 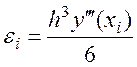. Оценка погрешности в точке х_n может быть получена с помощью двойного просчёта (с шагом h и h/2):

(13)

С.) Метод Рунге-Кутта. (4 го порядка)

Наиболее знаменитым из методов Рунге-Кутта является классический метод 4 го порядка

(14)

(15)

Грубая оценка погрешности (двойной просчёт): (16)

Где у(х_i) – точное решение, у * _i – приближённое решение с шагом h/2, y_i – … с шагом h _.

Для оценки правильности выбора шага h используют равенство:

(17)

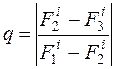
q должно равняться нескольким сотым, иначе h уменьшается.

D). Метод Рунге–Кутта 3-го порядка

Многошаговые методы.

(используют информацию о нескольких предыдущих точках)

Д ) Алгоритм Адамса.

Пусть дано дифференциальное уравнение: у′ = f(x, y) (1)

с начальными условиями: у(х₀) = у₀ (1*)

Требуется найти решение уравнения (1) на отрезке [a,b].

Разобьём отрезок [a,b] на n равных частей точками х_i = х₀ + ih (i =0, 1, …, n).

1 ый этап: стартовая процедура. Используют какой-либо одношаговый метод того же порядка точности до тех пор, пока не будет получено достаточно значений для работы многошагового метода.

2 ой этап: рекурсивной процедуры. Определение: у_k, y_k₊₁,…, y_n основано на интегрировании интерполяционного многочлена Ньютона.

Рабочие формулы явных методов Адамса (2-го, 3-го, 4-го порядков).

(2)

(3)

(4)

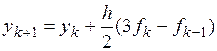
Формулы (2)-(4) называются экстраполяционными и на практике используются в качестве прогноза.

Для улучшения точности или коррекции результата применяют неявные методы (используют ещё ненайденные значения: у_k₊₁, y_k₊₂,…).

(5)

(6)

(7)

Формулы (5)-(7) называются интерполяционными.

Для грубой оценки точности (двойной просчёт):

Лекция 1

Приближённые методы решения СЛАУ

А) Метод простых итераций.(Метод последовательных приближений).

Пусть дана система n линейных уравнений с n неизвестными:

(1)

или где — заданные числа; .

Задаются произвольно n-чисел – нулевое приближение искомой функции.

Далее подставляем в правую часть системы (1) нулевое приближение и

находим первое приближение.

, (2)

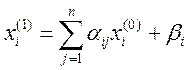
Затем по 1-ому приближению находят 2-ое, 3-е и т.д.

В результате для k-ого приближения получаем формулу:

, (2’)

Таким образом мы получили последовательность векторов

Х (0) ,Х (1) ,…, Х (К) , к=1,2,…

В равенстве (2’) перейдем к пределу при k→∞ при замене х_i на с_i.

Теорема(достаточные условия сходимости простой итерации):

Пусть выполняется хотя бы одно из следующих условий (нормы матрицы):

а) Если максимум суммы модулей коэффициентов при неизвестных (по строкам) меньше 1:

б) Если максимум суммы модулей коэффициентов при неизвестных (по столбцам) меньше 1:

в) Если сумма всех элементов в квадрате меньше 1.

Если выполняется хотя бы одно, тогда справедливы утверждения:

1)система (1) имеет единственное решение (С₁. С_n);

3)для приближенного равенства верны оценки (x₁ ( k ) ,…x_n ( k ) ) 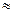(C_1,…C_n),

а’) есливыполняется условие а), то

б’) если выполняется условие б), то

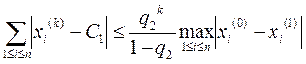
в’) если выполняется условие в), то

Замечания:

Б) Метод Зейделя.

Рассмотрим систему: 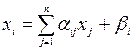i=1,n

Пусть матрица α удовлетворяет одному из условий теоремы:

Если, а) j. Аналогично, матрица называется нижнетреугольной, если все элементы выше главной диагонали (i

Точные и приближенные методы решения систем уравнений

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Электронный образовательный курс «Точные и приближенные методы решения систем уравнений» — это электронный ресурс, который содержит полный комплекс учебно-методических материалов, необходимых для освоения данной темы согласно учебному плану в рамках образвательной программы.

Курс обеспечивает все виды работ в соответствии с программой дисциплины, включая практикум, средства для контроля усвоения качества материала.

Основные цели создания электронного образовательного курса:

Повышение качества обучения при релизации образовательных программ с применением электронного обучения и дистационных образовательных технологий.

Оптимизация деятельности педагогического состава,работующего с применением электронного обучения и дистационных образовательных технологий.

Создание электронной информационно-образовательной среды, позволяющей осуществлять индивидуальный подход в образзовательном процессе.

Задачи создания электронного образовательного курса:

Соответствие единым требованиям к структре, отдельным элементам ЭОК и технологиям обучения в системе дистационного образования Ipsilon

Обеспечение образовательного поцесса учебно-методическими и контрольноизерительными материалами по теме «Точные и приближенные методы решения систем уравнений», реализуемой в системе дистанционного образования Ipsilon

Постоянное совершенствование и обновление комплекса учебно-методических материалов по данной теме.

Изучение данной темы является разделом традиционным и важным во всех периодах школьного образования. Данная работа актуальна с точки зрения освоения материала, для практического знания математики не только в курсе школьной программы, но и в углубленном изучении, а так же для практического применения.

Цель считается достигнутой, если ученик на уровнях:

а) имеет понятие о системах уравнений; б) решает системы методом подстановки, алгебраического сложения; в) сравнивает решение однотипных систем базового уровня сложности

а)правильно воспроизводит и использует термины, полученные знания в работе с различными методами решения систем уравнений ; б) имеет представление о системах однородных уравнений, выделяет базис доказательства; в) обобщает решение однотипных задач одного типа, составляет приемы их решения с помощью подсказки.

а) самостоятельно использует полученные знания; б)владеет матричным методом; в)разбирается и самостоятельно решает все виды систем, различными методами.

Цель 1 : контроль усвоения теоретических знаний при работе: а) с основными определениями; б) с методами решения систем уравнений; в) с типами и классами предлагаемых задач.

Цель считается достигнутой, если ученик на уровнях:

а) воспроизводит схему определения понятий и формулирует определения систем; приводит примеры; перечисляет методы решения; вставляет пропущенные в определении слова; раскрывает термин понятия; подводит объект под понятие; б) решает задачи базового уровня сложности.

а) формулирует определение систем уравнений, приводит контрпримеры; умеет доказывать и разбирается в методах решения; б) выполняет доказательство на своей модели; заполняет пустую готовую схему доказательства; называет базис доказательства; воспроизводит план доказательства; в) решает задачи среднего уровня сложности.

а) Работает с предоставленными задачами конкретного уровня, формулирует определение методов Гусса, Крамера и т.д. б) описывает основную идею доказательства; указывает на особенности методов; в) решает задачи повышенного уровня сложности.

Цель 2 : применение знаний и интеллектуальных умений при решении геометрических и учебных задач.

Цель считается достигнутой, если ученик на уровнях:

решает задачи своего уровня сложности: по готовым задачам определяет каким методом необходимо решить данную систему, по неполному условию находит и обосновывает применение метода, по условию без требования, решает системы, используя помощь.

Цель 3 : формирование коммуникативных умений через включение в групповую работу; взаимопомощь, рецензирование ответов, организацию взаимоконтроля и взаимопроверки на всех уровнях.

Цель считается достигнутой, если ученик:

а) работая в группе, ведет активную работу,оказывает помощь, анализирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием, организует взаимоконтроль; б) оказывает помощь работающим на предыдущих уровнях; в) составляет контрольную работу в соответствии со своим уровнем освоения темы.

Цель 4: формирование организационных умений (целеполагание, планирование, реализация плана, саморегуляция универсальных познавательных действий).

Цель считается достигнутой, если ученик:

формулирует цели своей учебной деятельности; б) выбирает задачи и решает их; в) осуществляет самопроверку; г) составляет контрольную работу для своего уровня усвоения; д) оценивает свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; е) делает выводы о дальнейших действиях, планирует коррекцию учебной познавательной деятельности.

Успешное освоение данного электронного образовательного курса окажет помощь при сдаче Основного государственного экзамена (ОГЭ) и Единого государственного экзамена (ЕГЭ).

Структура электронного образовательного курса

Предлагается следующий порядок изучения данного электронного курса. Сначала необходимо ознакомиться с модулем «Историческая справка». Данный модуль носит ознакомительный характер, поэтому можно сразу приступить к изучению модуля «Теоретическая часть». Этот модуль достаточно объемный, поэтому на его изучение отводится несколько дней. Учащиеся должны будут ознакомится с основными определениями, освоить различные методы решения систем таких как: метод подстановки, метод алгебраического сложения, метод введения новых переменных, метод замены переменных, далее ученик переходит на изучение более сложного методического материала, знакомится с системами однородных уравнений а также с матричным методом.

Далее учащимся после модуля «Теоретическая часть» предлагаются контрольные вопросы. Правильный ответ на каждый вопрос оценивается в полбалла. Вопросов всего 15, поэтому об успешном прохождении модуля можно будет говорить, набрав от 5 до 7,5 баллов (10-15 вопроса).

После изучения данных разделов можно браться за решение задач базового уровня сложности – это модуль 4. Каждая задача данного уровня будет оцениваться в 1 балл. Модуль считается успешно пройденным, если учащийся набрал от 5 до 7 баллов. Такое количество баллов можно приравнять к оценке «5». Если учащийся набрал от 4 до 5 баллов, это говорит о менее успешном освоении модуля и приравнивается к оценке «4», от 2 до 4 баллов – это оценка «3». Наконец, если набрано менее 7 баллов, значит, есть необходимость снова вернуться к изучению теоретической части.

После того как ученик освоил базовый уровень сложности, он переходит к модулю 5 «Тренировочные задачи среднего уровня сложности». Там также предлагаются 10 заданий, каждое из которых оценивается в 2 балла. Общее количество баллов, которое можно набрать на данном этапе составляет 14 баллов. Модуль считается успешно пройденным, если учащийся набирает от 10-14 баллов. Минимальное количество баллов которое может получить учащимся по прохождению данного теста составляет 6 баллов (3 задания)

Соответственно, 6 – 8 баллов – это оценка «3», 8 – 10 баллов – это оценка «4», 10-14 баллов – это оценка «5». Перевод в оценку необходим для самоконтроля, поэтому, если учащийся набрал менее 6 баллов, он получает оценку «2» и ему необходимо снова обратиться к теоретическому материалу.

Если ученик заинтересован на более углубленное изучение данной темы, ему рекомендуется вернуться в модуль 2″Теоретическая часть» и ознакомится с матричным методом решения систем уравнений. После изучения и освоения материала, предлагается приступить к модулю 6 «Тренировочные задачи повышенного уровня сложности». Таких заданий так же предлагается 7 и правильное решение каждой оценивается в 3 балла. Максимальное количество баллов, которое возможно набрать, составляет- 21 балл (7 заданий). Если учащийся набирает менее 9 баллов, говорит о том. что ему необходимо вернуться в модуль 2″Теоретический материал».

На освоение данного электронного образовательного курса в среднем можно затратить неделю. Но это касается учащихся 9-х классов, освоивших темы, необходимые для решения некоторых задач среднего и повышенного уровней сложности. Необходимо учитывать уровень знаний учащихся, и в каком классе предлагается прохождение данного курса.

Термин «С истема уравнений» — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.

Существует множество методов решения системы уравнений. Подход зависит от типа системы. Так, решение систем линейных уравнений полностью исследовано: у них найдены аналитические методы ( метод Крамера ) и предложено несколько численных как точных (простейший — метод Гаусса ), так и приближённых ( метод итераций ).

Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.

Габриель Крамер ( нем. Gabriel Cramer , 31 июля 1704 , Женева , Швейцария — 4 января 1752 , Баньоль-сюр-Сез, Франция ) -швейцарский математик, ученик и друг Иоганна Бернулли , один из создателей линейной алгебры .

И звестная теорема линейной алгебры, которая называется правилом Крамера, дает решение системы линейных уравнений в терминах определителей. Крамер опубликовал ее в книге “Введение в анализ алгебраических кривых” («Introduction à l’analyse des lignes courbes algébraique», 1750 год). В этой фундаментальной работе, в которой теория алгебраических кривых описана на основании ньютоновских принципов, впервые доказано, что кривая степени задается заданием ее точек. Для доказательства этого факта Крамера рассмотрел систему линейных уравнений, которую и решил новым методом, получившим название “метода Крамера”.

Иоганн Карл Фридрих Гаусс ( нем. Johann Carl Friedrich Gauß ; 30 апреля 1777 , Брауншвейг — 23 февраля 1855 , Гёттинген ) — немецкий математик , механик , физик , астроном и геодезист . Считается одним из величайших математиков всех времён, «королём математиков». Лауреат медали Копли (1838), иностранный член Шведской (1821) и Российской (1824) Академий наук, английского Королевского общества .

С именем Гаусса связаны фундаментальные исследования почти во всех основных областях математики: в алгебре , теории чисел , дифференциальной и неевклидовой геометрии , математическом анализе , теории функций комплексного переменного, теории вероятностей, а так же в аналитической и небесной механике, астрономии, физике и геодезии. «В каждой области глубина проникновения в материал, смелость мысли и значительность результата были поражающими. Гаусса называли „королём математиков»

Определение. Системой m линейных уравнений с n неизвестными называется система вида

где a _ij и b _i ( i =1,…, m ; b =1,…, n ) – некоторые известные числа, а x ₁ ,…,x _n – неизвестные. В обозначении коэффициентов a _ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы .

Числа, стоящие в правых частях уравнений, b ₁ . b _m называются свободными членами.

Определение. Совокупность n чисел c ₁ . c _n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c ₁ . c _n вместо соответствующих неизвестных x ₁ . x _n .

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

Система может иметь единственное решение.

Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.

И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x ₁ + x ₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной . В противном случае, т.е. если система не имеет решений, то она называется несовместной .

Рассмотрим методы нахождения решений системы.

2.Численные методы решения уравнений

2.1 Метод подстановки

Этот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений с двумя переменными х и у.

Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у.

1. Выразить у через х из одного уравнения системы.
2. Подставить полученное выражение вместо у в другое уравнение системы.
3. Решить полученное уравнение относительно х.
4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.
5. Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге.

Переменные х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой [1].

Пример 1. Решим систему уравнений

1) Выразим х через у из первого уравнения системы: х = 5 — 3у.
2)Подставим полученное выражение вместо х во второе уравнение системы: (5 -3у) у=2.
3)Решим полученное уравнение:

4) Подставим поочередно каждое из найденных значений у в формулу

Если то
5) Пары (2; 1) и решения заданной системы уравнений.

2.2 Метод алгебраического сложения

Этот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода рассмотрим на следующем примере.

Пример 2. Решим систему уравнений

Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения:

Вычтем второе уравнение системы из ее первого уравнения:

В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой:

Эту систему можно решить методом подстановки. Из второго уравнения находим . Подставив это выражение вместо у в первое уравнение системы, получим

Осталось подставить найденные значения х в формулу .

Таким образом, мы нашли два решения системы:

2.3 Метод введения новых переменных

С методом введения новой переменной при решении рациональных уравнений с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах [2].

Пример 3. Решим систему уравнений

Введем новую переменную . Тогда первое уравнение системы можно будет переписать в более простом виде: Решим это уравнение относительно переменной t:

Оба эти значения удовлетворяют условию , a потому являются корнями рационального уравнения с переменной t. Но значит, либо

, откуда находим, что х = 2у, либо ,

Таким образом, с помощью метода введения новой переменной нам удалось как бы «расслоить» первое уравнение системы, достаточно сложное по виду, на два более простых уравнения:

Далее каждое из двух полученных простых уравнений нужно поочередно рассмотреть в системе с уравнением х 2 — у 2 = 3, о котором мы пока не вспоминали. Иными словами, задача сводится к решению двух систем уравнений:

Надо найти решения первой системы, второй системы и все полученные пары значений включить в ответ. Решим первую систему уравнений:

Воспользуемся методом подстановки, тем более что здесь для него все готово: подставим выражение 2 у вместо х во второе уравнение системы. Получим:

Так как х = 2у, то находим соответственно х ₁ = 2, х ₂ = 2. Тем самым получены два решения заданной системы: (2; 1) и (-2; -1).

Решим вторую систему уравнений:

Снова воспользуемся методом подстановки: подставим выражение 2х вместо у во второе уравнение системы. Получим:

Это уравнение не имеет корней, значит, и система уравнений не имеет решений. Таким образом, в ответ надо включить только решения первой системы.

Метод введения новых переменных при решении систем двух уравнений с двумя переменными применяется в двух вариантах. Первый вариант: вводится одна новая переменная и используется только в одном уравнении системы. Именно так обстояло дело в примере 3.Второй вариант: вводятся две новые переменные и используются одновременно в обоих уравнениях системы. Так будет обстоять дело в примере 4.

Пример 4 . Решим систему уравнений

Введем две новые переменные:

Учтем, что тогда

Это позволит переписать заданную систему в значительно более простом виде, но относительно новых переменных а и b:

Применим для решения этой системы метод алгебраического сложения:

Так как а = 1, то из уравнения а + 6 = 2 находим: 1 + 6 = 2; 6=1. Таким образом, относительно переменных а и b мы получили одно решение:

Возвращаясь к переменным х и у, получаем систему уравнений, т.е.

Применим для решения этой системы метод алгебраического сложения:

Так как то из уравнения 2x + y = 3 находим:

Таким образом, относительно переменных х и у мы получили одно решение:

Метод разложения на множители.

Метод разложения на множители алгебраических систем двух уравнений с двумя неизвестными заключается в следующем. Если в алгебраической системе

то всякое решение системы уравнений

является решением совокупности систем

Пример 1. Решим систему

Заметим, что множитель так как в этом случае правая часть второго уравнения системы также обратилась бы в нуль. Следовательно, система (*) равносильна системе

Решим второе уравнение:

Выразив x из первого уравнения и подставив во второе, получили уравнения для нахождения y . В первое уравнение системы вместо y подставляем найденное значение и находим значения x

Теперь рассмотрим методы решения систем уравнений.

Метод исключения одной из неизвестных.

Метод исключения неизвестных позволяет последовательно сводить решение данной системы к решению системы (или совокупности систем), содержащей на одну переменную меньше. Этот метод последовательного исключения основан на очевидном утверждении, что система уравнений

равносильна системе уравнений

и аналогично для большего числа переменных.

Пример 2 . Решим систему

Левые части уравнений системы содержат одни и те же комбинации неизвестных. Умножим уравнения на подходящие множители с тем, чтобы исключить из системы одно из неизвестных. Из системы исключим сложив второе уравнение с первым, умноженным на -3. В результате получаем уравнение .

Решим данное уравнение путем замены.

Пусть xy = t , тогда ,

Таким образом, исходная система распадается на системы:

В первом случае находим x 2 =1. Если x=1 то y=2 , а если x=-1 , то y=-2 .

Во втором случае, исключая , получаем x 2 =-209 . Поэтому вторая из двух последних систем не имеем действительных решений.

Метод алгебраических преобразований уравнений системы.

Уравнения системы можно складывать, вычитать, умножать на число, перемножать, делить, соблюдая при этом возможность выполнения таких операций. Заметим, что следствие системы, получаемое в результате алгебраических преобразований, содержит все решения исходной системы, и, кроме того, оно может содержать лишние корни.

1) если следствие не имеет решений, то и исходная система не имеет решений;

2) если решениями следствия окажутся действительными числа, то их нужно подставить в исходную систему и проверить, являются ли они ее корнями;

3) если решениями следствиями окажутся алгебраические выражения, то их нужно рассматривать совместно с уравнениями исходной системы. В этом случае получим равносильную систему или совокупность систем [3].

Пример 3. Решим систему

2.4 Метод замены переменных

Метод замены неизвестных основан на следующем утверждении.

Пусть дана система уравнений

и пусть система

имеет k различных решений

Тогда система (7) равносильна совокупности k систем

Пример 4 . Решим систему

Произведем замену. Пусть . Тогда

Складывая уравнения, получим

Преобразуем первое уравнение:

2.5 Системы однородных уравнений

Определение : Система двух уравнений с двумя переменными вида

называется однородной (левые части обоих уравнений однородные многочлены степени n от двух переменных).

Однородные системы решаются комбинацией двух методов: линейного преобразования и введения новых переменных.

Пример 5. Решим систему

Решение . Первое уравнение системы однородное (напомним, что уравнение вида f(x,y)=0 где f(x,y) — однородный многочлен — называется однородным уравнением). Заметим, что если положить y=0 то из однородного уравнения 3x 2 +xy-2y 2 =0 находим x=0. Но пара чисел (0;0) не удовлетворяет второму уравнению системы, поэтому y≠0 и, следовательно, обе части однородного уравнения 3x 2 +xy-2y 2 =0 можно разделить на y 2 (это не приведёт к потере корней).

Получим и , откуда находим, что или , т.е. x= — y или .

Типичные ошибки при решении систем и методы их устранения.

При решении некоторых систем иногда происходит потеря корней в ответе или появляются посторонние корни. Основная причина этого заключается в том, что осуществляются правдоподобные рассуждения, но теряется контроль над равносильностью переходов от одной системы к другой. Для того чтобы избежать подобных ошибок, нужно знать природу их появления и на определенном этапе решения произвести необходимые преобразования, проверку решения и т.д.

В качестве таких примеров рассмотрим решение нескольких систем нелинейных уравнений.

Пример 1. Решим систему уравнений

Неправильное решение . Вычтем из первого уравнения системы второе уравнение. Получим откуда x =11.

В этом случае корень уравнения, полученный после эквивалентного преобразования (вычли второе уравнение из первого), не проверили. Чтобы избежать подобной ошибки, необходимо после вычитания одного уравнения из другого решать систему уравнений, в которой обязательным является наличие уравнения, полученное после вычитания и одного из первоначальных уравнений.

Выполним эквивалентные преобразования:

Таким образом, при решении системы уравнений, необходимо записать такое же количество уравнений, которое было в условии, чтобы не получить посторонний корень.

Правильный ответ: .

Пример 2 . Решим систему уравнений

Решение . Выполним тождественное преобразование: разделим первое уравнение системы на второе уравнение, получим:

Решая систему методом подстановки, получим множество решений: <(3;0); (0;3)>.

Система (13) получена из системы (12) делением на число, отличное от нуля, поэтому системы (12) и (13) эквивалентны.

При решении систем нелинейных уравнений необходимо помнить о том, что такое тождественное преобразование как деление одного уравнения на другое не всегда приведет к правильному решению, так как может произойти потеря корня. Покажем это на следующем примере.

Пример 3 . Решим систему уравнений

Но в этом случае произошла потеря решения <(2;0)>. Это произошло потому, что при делении не было наложено условие . Рассматривая условие , получаем х = 2.

Значит, метод деления одного уравнения на другое не безупречен, т.е.
к системе
можем потерять решения.

2.6 Матричный метод

Основные понятия при работе с матричным методом.

Определение. Матрица – это система элементов (функций, чисел и др. величин), которые расположены в виде прямоугольной таблицы. Общий вид записи матрицы представлен ниже:

Произвольный элемент матрицы обозначается через a _ij (элемент i -й строки и j -го столбца). Тем, кто знаком с основами алгоритмизации и программирования, будет проще, если сравнить матрицу с двумерным массивом данных (в частном случае с одномерным массивом). Матрица имеет размерность, определяемую количеством строк и столбцов.

Основными действиями над матрицами являются:

сравнение (для матриц одинаковой размерности):

сложение и вычитание (для матриц одинаковой размерности):

умножение (количество столбцов первой матрицы равно количеству строк второй матрицы):

источники:

http://lektsia.com/4xd11.html

http://infourok.ru/tochnie-i-priblizhennie-metodi-resheniya-sistem-uravneniy-3823393.html