Приближенные методы решения уравнений численные методы

Численные методы решения уравнений

Нахождение корней уравнений — одна из наиболее часто встречающихся задач. Вместе с тем не всегда есть возможность найти аналитическое решение уравнения. В первую очередь это относится к большинству трансцендентных уравнений, т.е. уравнений, в которых неизвестная х находится под знаком трансцендентной функции, например, x 2 — sin 5x = 0.

Доказано также, что не имеют аналитического решения алгебраические уравнения степени выше четвертой:

Для поиска корней таких уравнений используются численные (приближенные) методы, которые по своей сути являются способами уточнения корней 4.

В общем случае запись нелинейного уравнения имеет вида

Задача решения нелинейного уравнения состоит из двух этапов:

1) локализация корней, т.е. определение интервала изоляции (интервала неопределенности), в котором расположен корень;

2) определение с заданной точностью точности ε приближенного значения корня.

Для локализации корней можно воспользоваться следующей теоремой.

Теорема: Если непрерывная функция y=f(x) на концах отрезка [a, b] принимает значения разных знаков, т.е. f(a)·f(b)

и вычисляется значение функции f(d).

Далее делается выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Для чего проверяется условие

Блок-схема метода половинного деления представлена на рисунке 12.

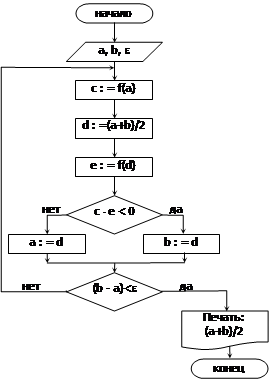Рисунок 12 — Блок-схема алгоритма поиска корней уравнения методом половинного деления

Метод хорд

Идея метода хорд заключается в том, что кривая y=f(x) на участке [a, b] заменяется хордой и в качестве приближенного значения корня х * =x_n принимается точка пересечения оси абсцисс с хордой (рисунок 13).

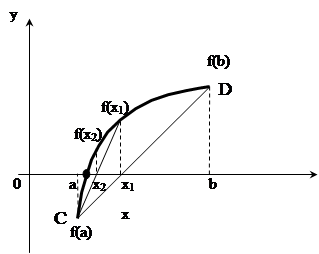Рисунок 13 – Графическая интерпретация метода хорд

Запишем уравнение хорды, проходящей через точки С с координатами (a, f(a)) и D – (b, f(b)):

.

Абсцисса точки пересечения хорды с осью ОХ находится из этого выражения при y=0, т.е.

.

Выполнив преобразования, получаем выражение для нахождения приближенного корня:

. (35)

Полученное значение x_n можно снова использовать для дальнейшего уточнения корня, рассматривая интервал [a, x_n] или [x_n , b] в зависимости от знака функции в точке x_n — f(x_n).

Если значения функции при х=а и х=x_n имеют разные знаки, т.е. выполняется условие

Вычисления повторяются до тех пор, пока выполняется условие

Блок-схема, реализующая метод хорд, приведена на рисунке 14.

Метод Ньютона (метод касательных)

Этот метод основан на замене функции y=f(x) в точке начального приближения x=x₀ касательной, пересечение которой с осью х дает первое приближение корня х₁ и т.д. (рисунок 15).

В качестве x₀ выбирают тот конец отрезка [a, b] (т.е. точку С или точку D), для которого выполняется условие:

Рисунок 14 — Блок-схема алгоритма поиска корней уравнения методом хорд

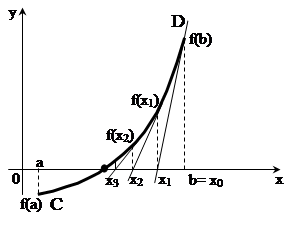Рисунок 15 – Графическая интерпретация метода Ньютона

Для графической иллюстрации (рисунок 15), где начальное приближение находится в точке D, т.е. x₀=b, запишем:

,

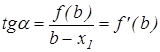
откуда 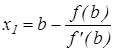или .

Тогда, в общем виде выражение для нахождения корня можно записать:

Итерационный процесс уточнения корня выполняется до тех пор, пока соблюдается условие

Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения 10 -5 — 10 -6 достигается через 5-6 итераций.

Блок-схема, реализующая метод Ньютона, приведена на рисунке 16.

Рисунок 16 — Блок-схема алгоритма поиска корня уравнения методом Ньютона

Комбинированные методы

Комбинированные методы решения уравнения основаны на сочетании описанных выше методов и позволяют получить приближение к корню с противоположных сторон с сужением интервала локализации корня.

Оба метода используются последовательно, при этом интервал локализации сравнивается с заданной точностью e. Корень уравнения находится как среднее двух значений, полученных каждым из методов.

На рисунке 17 приведена блок-схема комбинированного метода хорд-Ньютона.

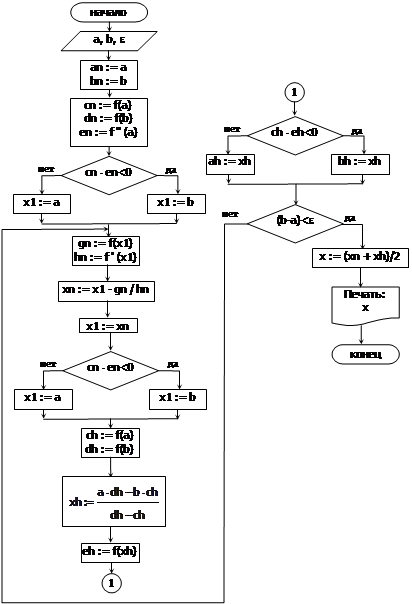Рисунок 17 — Блок-схема комбинированного метода хорд-Ньютона

Лекция «Численные методы решения уравнений»
учебно-методический материал

Лекция по разделу «Численные методы».

Рассматриваются следующие методы решения алгебраических и трансцендентных уравнений:

1) метод дихотомии (метод деления отрезка пополам),

3) метод касательных,

4) метод итераций.

Скачать:

Предварительный просмотр:

Тема 12.2.Приближенное решение алгебраических и трансцендентных уравнений.

Задача о нахождении приближенных значений действительных корней уравнения f(x)=0 предусматривает предварительное отделение корня , т.е. установления промежутка, в котором других корней данного уравнения нет.

Будем предполагать, что функция f(x) в промежутке [a; b] непрерывна вместе со своими производными f’(x) и f’’(x) , значения f(а) и f(b) функции на концах промежутка имеют разные знаки, т.е. f(а) ∙ f(b) , и обе производные f’(x) и f’’(x) сохраняют знак во всем промежутке [a; b].

Т.к. действительными корнями уравнения f(x)=0 являются абсциссы точек пересечения кривой y=f(x) с осью ОХ , то отделение корня можно произвести графически.

Иногда полезно уравнение f(x)=0 записать в виде . Действительными корнями исходного уравнения служат абсциссы точек пересечения графиков функций .

Мы рассмотрим 4 численных решения уравнений.

1. Метод дихотомии (метод деления отрезка пополам).

Этот метод можно использовать когда нам предположительно или точно известны границы отрезка, содержащего корень и на этих границах f(x) принимает значения разных знаков, тогда по теореме о достаточных условиях существования корня на заданном отрезке существует хотя бы один корень.

y

1. Делим отрезок [a; b] пополам.
2. Определяем, на границах какой из частей первоначального интервала функция f(x) меняет знак.
3. Полученный интервал снова делим на две части и т.д.

Такой процесс продолжаем до тех пор, пока не перестанут изменяться сохраняемые в ответе десятичные знаки.

Пусть требуется вычислить действительный корень уравнения f(x)=0 , изолированный на отрезке [a;b]. Рассмотрим график функции у= f(x) . Пусть f(а) и f(в) >0. Точки графика А[a;f(a)] и В[b;f(b)] соединим хордой .За приближенное значение искомого корня примем абсциссу х 1 точки пересечения хорды АВ с осью Ох .

Это приближенное значение находится по формуле , где x 1 ∈ (a;b)

Пусть, например, f(x 1 ) тогда за новой (более узкий) промежуток изоляции корня принять [x 1 ,b].

Соединив точки А 1 [x 1 ;f(x 1 )] и В[b;f(b)] , получим в точке пересечения хорды с осью Ох второе приближение x 2 , которое вычислим по формуле: и т.д.

Последовательность чисел a 1 , x 1 , x 2 ,… стремится к искомому корню уравнения f(x)=0 .Вычисление приближенных значений корней уравнения следует вести до тех пор, пока не перестанут изменятся те десятичные знаки, которые мы хотим сохранить в ответе (т.е.пока не будет достигнута заданная степень точности)

Если Х-точный корень уравнения f(x)=0 , изолированный на отрезке [а,в] , а ξ- приближенное значение корня ,найденное методом хорд ,то оценка погрешности этого приближенного значения такова:

1. Метод касательных (Метод Ньютона)

Пусть действительный корень уравнения f(x)=0 изолирован на отрезке [а,в] . Будем предполагать, что все ограничения, сформулированные выше относительно f(x) , сохраняют силу и в этом случае. Выделяем на отрезке [а,в] такое число x 0 , при котором f(x 0 ) имеет тот же знак, что и f’’(x 0 ) т.е. f(x 0 ) f’’(x 0 )>0 (в частности , за x 0 может быть принят тот из концов отрезка [а,в] , в котором соблюдено это условие). Проведем в точке Мо[x 0 , f(x 0 )] касательную к кривой y=f(x) .

y= f(x)

За приближенное значение корня примем абсциссу точки пересечения этой касательной с осью Ох . Это приближенное значение корня находится по формуле: .

Применив этот прием вторично в точке M 1 [x 1 ; f(x 1 )] , найдем и т.д.

Полученная т.об. последовательность x 0 , x 1 , x 2 ,… имеет своим пределом искомый корень.

Для оценки погрешности приближенного значения корня, найденного, методом Ньютона, может быть .использовано неравенство:

4. Метод итераций.

Если данное уравнение приведено к виду , где всюду на отрезке [а,в] , на котором исходное уравнение имеет единственный корень, то исходя из некоторого начального .значения x 0 , принадлежащего отрезку [а,в] , можно построить такую последовательность: …

Пределом этой последовательности является единственный корень уравнения f(x)=0 на отрезке [а,в]. Погрешность приближенного значения x n корня Х , найденного методом итерации, оценивается неравенством.