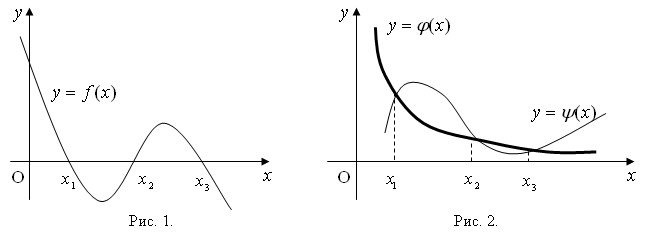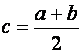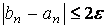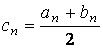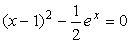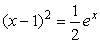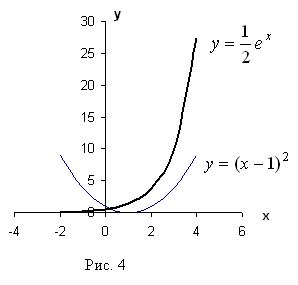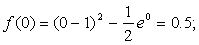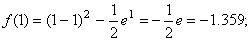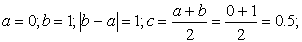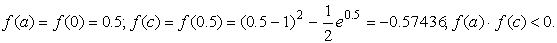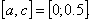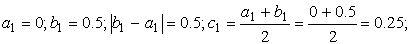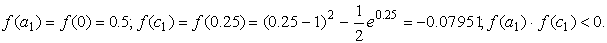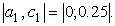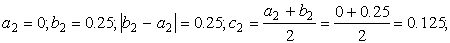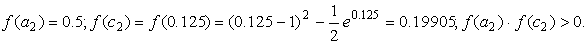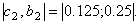Приближенные методы вычисления нелинейных уравнений

Приближенные методы вычисления нелинейных уравнений

Pers.narod.ru. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений

1. Приближенное решение нелинейных алгебраических уравнений

Дано нелинейное алгебраическое уравнение

Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.

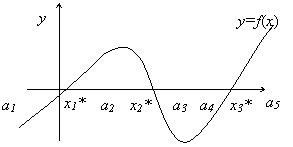
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x₁*, x₂*, x₃*, в которых функция f(x) пересекает ось x.

Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.

В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <x_n>, такой, что 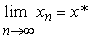. По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |x_n – x*| / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.

Если корней несколько, то для каждого нужно найти интервал изоляции.

Существуют различные способы исследования функции: аналитический, табличный, графический.

Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при 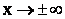и нахождение участков возрастания и убывания функции.

Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.

Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.

Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.

Найдем производную f / (x)=3x 2 -12x+3.

Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;

X₁=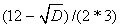= 0.268;

X₂=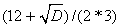= 3.732;

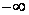
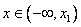
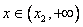
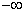
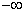
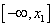
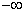
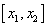
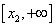
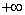
Так как f / ()>0, то f / (x)>0 при , f / (x) / (x)>0 при . Кроме того, f()= 0. Следовательно, на интервале возрастает от до f(x₁)= 3x₁ 2 -12x₁+3=11.39; на интервале — убывает до f(x₂)= 3x₂ 2 -12x₂+3=-9.39 и на интервале возрастает до , т.е. уравнение имеет три корня.

Найдем интервалы изоляции для каждого из корней.

Рассмотрим для первого корня отрезок [-2, -1]:

f(-2)= -27 0, f / (x)>0 при 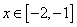т.е. этот отрезок является интервалом изоляции корня.

Рассмотрим для второго корня отрезок [1, 3]:

f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при 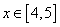т.е. этот отрезок является интервалом изоляции корня.

Приближенные методы вычисления нелинейных уравнений

1. Приближенное решение нелинейных уравнений

Пусть дано уравнение с одним неизвестным

, (1.1)

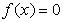
где f ( x ) — заданная алгебраическая или трансцендентная функция.

Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций — показательная , логарифмическая, тригонометрические, обратные тригонометрические.

Решить уравнение — значит найти все его корни, то есть те значения х , которые обращают уравнение в тождество, или доказать, что корней нет.

В общем случае не существует формул, по которым определяются точные значения корней уравнения (1.1). Для отыскания корней используют приближенные методы, при этом корни находятся с некоторой заданной точностью ε . Это означает, что если x — точное значение корня уравнения, а x ’ — его приближенное значение с точностью ε , то | x — x ’ | ≤ ε . Если корень найден с точностью ε , то принято писать x = x ± ε .

Будем предполагать, что уравнение (1.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.

Приближенное решение уравнения состоит из двух этапов:

1. Отделение корней, то есть нахождение интервалов из области определения функции f ( x ), в каждом из которых содержится только один корень уравнения (1).

2. Уточнение корней до заданной точности.

Отделение корней можно проводить графически и аналитически.

Для того , чтобы графически отделить корни уравнения (1.1), строят график функции y = f ( x ). Абсциссы точек его пересечения с осью Ox есть действительные корни уравнения (рис. 1). Практически бывает удобнее заменить уравнение (1.1) равносильным ему уравнением

, (1.2)

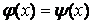
где Φ( x ) и Ψ( x ) — более простые функции, чем f ( x ). Абсциссы точек пересечения графиков функций y = Φ( x ) и y = Ψ( x ) дают корни уравнения (1.2), а значит и исходного уравнения (1.1) (рис.2).

Аналитическое отделение корней основано на следующей теореме: если непрерывная на отрезке [ a , b ] функция y = f ( x ) принимает на концах отрезка значения разных знаков, т.е. f ( a )· f ( b ) f ( x ) = 0; если при этом производная f ’ ( x ) сохраняет знак внутри отрезка [ a , b ], то корень является единственным.

Уточнение корней заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Рассмотрим самый простой из них — метод половинного деления.

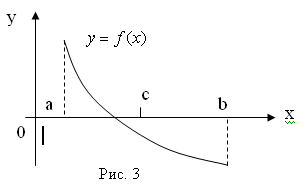
Пусть корень отделён и принадлежит отрезку [ a , b ]. Находим середину отрезка [ a , b ] по формуле

Если f ( c ) = 0, то с — искомый корень. Если f ( c ) ≠ 0, то в качестве нового отрезка изоляции корня [ a ₁ , b ₁ ] выбираем ту половину [ a , c ] или [ c , b ], на концах которой f ( x ) принимает значения разных знаков. Другими словами, если f ( a ) ∙ f ( c ) a , c ], если f ( a ) ∙ f ( c ) — отрезку [ c , b ]. Полученный отрезок снова делим пополам, находим c₁ ,

вычисляем f ( c ₁ ), выбираем отрезок [ a ₂ , b ₂ ] и т.д. Длина каждого нового отрезка вдвое меньше длины предыдущего, то есть за n шагов отрезок сократится в 2 n раз. Как только будет выполнено условие

то в качестве приближенного значения корня, вычисленного с точностью ε , можно взять

Пример . Пусть требуется решить уравнение

с точностью ε = 0,0001. Отделим корень графически. Для этого преобразуем уравнение к виду

и построим графики функций (рис. 4):

Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку [0; 1].

Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка [0; 1] имеем:

. Следовательно, корень отделён правильно.

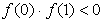
Уточнение корня выполним методом половинного деления.

Корень принадлежит отрезку

Корень принадлежит отрезку

Корень принадлежит отрезку

Методы приближенного решения нелинейных уравнений

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Приближённые методы решения уравнений.

Рассмотрим задачу нахождения нулей функции f ( x ), т.е. корней уравнения f ( x )=0. п редположим, что интересующий нас корень изолирован, т.е., что найден содержащий его промежуток [ a , b ], в котором других корней нет.

Если на концах отрезка [ a , b ] функция f ( x ) имеет значения f ( а ) и f ( b ) разных знаков, то по 1 теореме Больцано — Коши, деля на части а _k , b _k , содержащее корень, и определяя знак функции f в точках деления, можно произвольно сужать этот промежуток и таким образом осуществлять приближённое вычисление корня. Однако этот приём, не смотря на его принципиальную простоту, на практике часто оказывается непригодным, так как требует слишком большого количества вычислений.

Рассмотрим основные приёмы приближённого вычисления изолированного корня уравнения f ( x ) = 0. При этом будем использовать основные понятия и методы дифференцированного исчисления.

Теорема. Пусть выполнены следующие условия:

(1) функция f в промежутке [ a , b ] непрерывна вместе со своими производными f ( x ) и f ( х );

(2) значения f ( а ) и f ( b ) функции на концах промежутка имеют разные знаки f ( а ) f ( b ) 0;

(3) обе производные f ‘ ( x ) и f ( х ) сохраняют каждая определённый знак на всём промежутке [ a , b ].

Тогда уравнение f ( x )=0 на этом промежутке имеет единственный корень.

Следствия: Из непрерывности функции f и условия (2) следует, что между а и b содержится корень уравнения f ( x ) = 0. Так как производная f ( x ) сохраняет знак, то f в промежутке [ a , b ]возрастает или убывает и, следовательно, обращается в 0 лишь однажды, корень изолирован.

Условие (3) геометрически означает, что кривая y = f ( x ) не только идёт в одном направлении, но к тому же строго выпукла или вогнута, смотря по знаку f ( х ) . На чертеже изобразим 4 возможных случая, соответствующих различным комбинациям знаков f ( x ) и f ( х ) .

Если промежуток [ a , b ] достаточно мал, то с приближением можно считать, что при изменении х в его пределах — приращение функции f ( x ) пропорционально приращению аргумента. Обозначая через корень функции, имеем, в частности, , откуда, с учётом того, что f ( ) = 0,

Таким образом, за приближённое значение корня принимается число

Это выражение можно представить и в такой форме:

Изложенное правило получения приближённого значения корня называется правилом пропорциональных частей . Оно допускает простое геометрическое истолкование. Заменим дугу М ₁ М ₂ хордой М ₁ М ₂ . Уравнение хорды может

быть записано в виде:

Правило по существу сводится к тому, что вместо точки пересечения с осью Ox дуги М ₁ М ₂ мы находим точку пересечения с осью O х её хорды.

Действительно, полагая в уравнении хорды y = 0 для абсциссы х ₁ точки D , мы получаем именно выражение (1). В связи с этим правило пропорциональных частей называют методом хорд .

Рассмотрим вопрос о положении точки х ₁ по отношению к корню . Ясно, что точка х ₁ лежит между а и b , но с какой стороны от ?

В случаях I и IV А левее D , а в случаях II и III — А правее D . Ограничимся случаями I и IV , применим снова выведенное правило, на этот раз к промежутку [ x ₁ , b ], заменяя в (1) а на х ₁ , получим новое приближённое значение корня :

содержащееся, между х ₁ и . Этот процесс можно продолжать неограниченно и построить последовательность возрастающих приближённых значений:

При этом любые два последовательных значения х _n и х _{n + 1} связаны формулой:

Таким образом, применив достаточное число раз указанное выше правило, можно вычислить корень с любой степенью точности.

Правило Ньютона (метод касательных).

Пусть f удовлетворяет тем же условиям:

(1) f ( x ) непрерывна в [ a , b ] вместе со своими производными f ‘ , f ” ;

(2) f ( a ) и f ( b ) имеют разные знаки;

(3) обе производные f ‘ и f « сохраняют каждая определённый знак во всём [ a , b ].

Кроме того, искомый корень f ( x )=0 изолирован в [ a , b ]: a b . Отправляясь от какого-нибудь из концов этого промежутка, например, от b , запишем формулу Тейлора с дополнительным членом в форме Лагранжа:

Отбрасывая дополнительный член, приближённо положим: f ( b ) +f’ ( b )( — b )=0, откуда . Таким образом, мы приходим к приближённому значению корня : (2).

Получение этого значения можно наглядно использовать геометрически.

Рассмотрим касательную к кривой y = f ( x ) в точке М ₂ с абсциссой b . Её уравнение имеет вид: y — f ( b )= f ‘ ( b )( x — b ) . Полагая здесь у =0, найдём абсциссу точки Т ₁ пересечения касательной с осью О x , она в точности совпадает с точкой х ₁ , найденной выше. Значит, суть дела в приближённой замене дуги

кривой М ₁ М ₂ — касательной к ней в одном из её концов.

Это правило, называемое именем Ньютона, называется также методом касательных .

Аналогично, если исходить из точки а , и касательную к кривой провести в точку М ₁ (с абсциссой а ), то взамен (2), получим приближённое значение . Относительно вычисленного по этой формуле значения можно установить, как и выше: если значение f « ( x ) имеет одинаковый знак с f ‘( x ), то x ₁ лежит между а и . Таким образом, для каждого из четырёх возможных случаев понятно, с какого конца гарантирована успешность приближения к корню по правилу Ньютона. Повторное применение его в случаях I и IV дает последовательность убывающих значений:

а в случаях II и III — последовательность возрастающих значений:

Причём вычисление последующего значения по предыдущему всегда производится по формуле:

Этот метод состоит в одновременном использовании как метода касательных, так и метода хорд. Для определённости предположим, что мы имеем дело со случаем I .

вычислим по формулам:

О a b x тогда по доказанному:. При следующем же шаге мы заменяем в этих формулах a и b на x ₁ и x ₁ ‘ :

Этот процесс можно продолжать; имея два приближённых значения x _n и x _n ‘ , между которыми содержится корень , мы переходим к следующей паре приближенных значений по формулам:

Таким образом, при комбинированном методе мы получаем одновременно с недостатком и с избытком приближённые значения корня, которые стремятся к точному с разных сторон.

Рассмотрим вначале сущность итерационного метода. В отличие от прямых или точных методов, итерационные дают возможность получить решение лишь приближенно, путем повторения некоторой совокупности операций, позволяющей по исходному приближенному значению решения определить его уточненное значение. Выполнение этой совокупности операций составляет одну итерацию. Многократное повторение итераций позволяет получать все более точное решение при условии, что итерационный процесс сходится к искомому решению.

Если данное уравнение f ( x )=0 приведено к виду x = ( x ), где ‘( х ) r 1 всюду на отрезке [ a , b ], на котором оно имеет единственный корень, то исходя из некоторого начального значения х ₀ , принадлежащего отрезку [ a , b ], можно построить такую последовательность: х ₁ = ( х ₀ ), х ₂ = ( х ₁ ),…, х _n = ( x _{n -1} ),… . Пределом этой последовательности является единственный корень уравнения f ( x )=0 на отрезке [ a , b ].Погрешность приближенного значения x _m корня определяется неравенством: .

Замечание 1. Уравнение y = f ( x ) можно записать иначе. Одним из самых распространенных представлений является представление в виде: x = x + cf ( x ), где с — произвольная постоянная.

Замечание 2. Для нахождения приближенного значения корня с погрешностью, не превышающей , достаточно определить m так, чтобы выполнялось неравенство .