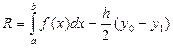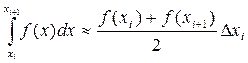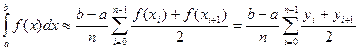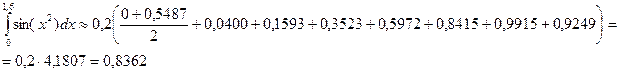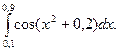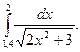Приближенные аналитические решения обыкновенных дифференциальных уравнений Текст научной статьи по специальности « Компьютерные и информационные науки»
Аннотация научной статьи по компьютерным и информационным наукам, автор научной работы — Васильев Александр Николаевич, Тархов Дмитрий Альбертович, Шемякина Татьяна Алексеевна
Рассматриваются подходы к построению многослойных приближённых решений дифференциальных уравнений . Эти подходы основаны на классических приближённых методах. В отличие от классических подходов в результате вычислений получаются не поточечные приближения, а приближённые решения в виде функций. Данные методы могут быть применены для генерации сколь угодно точных приближённых нейросетевых решений без трудоёмкой процедуры обучения. Проведены вычислительные эксперименты на тестовых задачах.
Похожие темы научных работ по компьютерным и информационным наукам , автор научной работы — Васильев Александр Николаевич, Тархов Дмитрий Альбертович, Шемякина Татьяна Алексеевна
Текст научной работы на тему «Приближенные аналитические решения обыкновенных дифференциальных уравнений»
Васильев А.Н., Тархов Д.А., Шемякина Т.А.
Санкт-Петербургский политехнический университет Петра Великого, Санкт-Петербург, Россия
ПРИБЛИЖЕННЫЕ АНАЛИТИЧЕСКИЕ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Рассматриваются подходы к построению многослойных приближённых решений дифференциальных уравнений. Эти подходы основаны на классических приближённых методах. В отличие от классических подходов в результате вычислений получаются не поточечные приближения, а приближённые решения в виде функций. Данные методы могут быть применены для генерации сколь угодно точных приближённых нейросетевых решений без трудоёмкой процедуры обучения. Проведены вычислительные эксперименты на тестовых задачах.
Нейронные сети; приближенные решения; дифференциальные уравнения.
Vasilyev A.N., Tarkhov D.A., Shemyakina T.A.
Peter the Great St. Petersburg Polytechnic University, Saint Petersburg, Russia
APPROXIMATE ANALYTICAL SOLUTIONS OF ORDINARY DIFFERENTIAL
Original approaches to building multi-layered approximate solutions of differential equations are discussed. These approaches are based on classical approximate methods. In contrast to classical approaches, we obtain as the result of the calculation not pointwise approximations but approximate solutions as functions. These methods can be applied for generating arbitrarily accurate approximate neural network solutions without time-consuming learning procedure. Computational experiments were carried out on several test problems.
Neural networks; approximate solutions; differential equations. Введение
Мы неоднократно отмечали в качестве одного из преимуществ неиросетевого моделирования над классическими подходами к построению приближенных решении дифференциальных уравнении (типа метода сеток) то обстоятельство, что неиросетевои подход позволяет получить решение в виде аналитическои формулы, а не набора числовых значении [1-5, 7-14]. В даннои работе показано, что это не совсем верно: задаваемые аналитически приближения для решения можно получить на основе более общих подходов, куда неиросетевои входит как частныи случаи. На примере обыкновенных дифференциальных уравнении с помощью метода Эилера и некоторых его обобщении получены приближенные аналитические решения. Обычные оценки точности исходных классических методов позволяют получить удобные оценки точности полученных приближении.
Данныи подход несложно распространить и на другие алгоритмы подобного типа. Так, например, этот подход распространяется на сеточные методы решения дифференциальных уравнении в частных производных. С помощью данного подхода, в частности, можно получить многослоиные неиросетевые приближенные решения дифференциальных уравнении без трудоемкои процедуры обучения. Получившиеся таким образом неиронные сети можно обучить с помощью классических методов [6].
Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнении
на промежутке D = [х0; х0 + а]. Здесь х е В с □ , у с □ р, f : □ р ^ □ р. Классический метод Эйлера состоит в разбиении промежутка В на п частей: х0 у к), (7)
при этом У1 = У о + ¥ (Хо + Уо + у Ъ (Хо, Уо)).
Применяем уточненныи метод Эилера (7) при п = 2, тогда получаем формулу
уп (х) = 1 — о.5х^т1 (8)
Графики данного приближенного решения уп (х) и решения у(х), построенного с помощью встроеннои операции МаШетайса 10, при а = 1;2;3 выглядят следующим образом:
Рис. 3. Графики приближённого решения yn (x) из (8) и y (x), построенного с помощью Mathematica 10, при
На рис.3 видим, что точность приближённого решения yn (x) из формулы (8) существенно выше, чем приближенного решения, полученного применением метода Эилера по формуле (6).
С увеличением количества разбиении n = 5 уточненныи метод Эилера (7) представим формулои
yn (x) = 1 — 0.0168х2а- 0.32х2а sin Ti — 0.0168x2a]-
— 0.16x2a sin [i- 0.0168x2a — 0.16x2a sin [i — 0.0168x2a]]
Графики данного приближенного решения yn (x) и решения y(x), построенного с помощью встроеннои операции Mathematica 10, при а = 1;2;3 практически сливаются:
Рассмотрим метод средней точки из книги [6]:
y *+1 = y * + hf (** + у, y * + y f(**, y *)) [10]
Применяем метод среднеи точки (10) при n = 2, тогда получаем формулу
yn (x) = 1- 0.316х2а — 0.125×2« sin [1 — 0.105х2а] (11)
Графики данного приближённого решения уп (х) и решения у(х), построенного с помощью встроенной операции МаШетайса 10, при а = 1;2;3 выглядят следующим образом:
Точность приближенного решения (11) еще выше, чем у формулы, получающеися применением уточненного метода Эилера (7) — (9). Применяем метод среднеи точки (10) при п = 5, тогда получаем формулу
уп (х) = 1 — 0.151х2а — 0.12х2а Sin[1 — 0.0337х2а] — 0.02х2а Sin[1 — 0.0168х2а] —
— 0.02х2а Sin[1 — 0.05х2а — 0.02х2а Sin[1 — 0.0168х2а]] —
-0.08×2аSin[1 — 0.0673х2а — 0.02×2аSin[1 — 0.0337х2а] — 0.02х2а Sin[1 — 0.0168х2а]] —
-0.02х2а Sin[1 — 0.0841х2а — 0.04х2а Sin[1 — 0.0337х2а] -0.02х2аЗт[1 — 0.0168х2а] —
— 0.02х2а Sin[1 — 0.05х2а — 0.02х2а Sin[1 — 0.0168х2а]]] —0.04х2а Sin[1 — 0.1х2а — 0.06х2а Sin[1 — 0.0337х2а] — 0.02х2а Sin[1 — 0.0168х2а] —0.02х2а Sin[1 — 0.05х2а — 0.02х2а Sin[1 — 0.0168х2а]] —
-0.02х2а Sin[1 — 0.0673х2а — 0.02х2а Sin[1 — 0.0337х2а] — 0.02х2а Sin[1 — 0.0168х2а]]] —0.02х2а Sin[1 — 0.119х2а — 0.08х2а Sin[1 — 0.0337х2а] — 0.02х2а Sin[1 — 0.0168х2а] —0.02х2а Sin[1 — 0.05х2а — 0.02х2а Sin[1 — 0.0168х2а]] —
-0.04х2а Sin[1 — 0.0673х2а — 0.02х2а Sin[1 — 0.0337х2а] — 0.02х2а Sin[1 — 0.0168х2а]] —0.02х2а Sin[1 — 0.0841х2а — 0.04х2а Sin[1 — 0.0337х2а] — 0.02х2а Sin[1 — 0.0168х2а] —0.02х2а Sin[1 — 0.0505х2а — 0.02х2а Sin[1 — 0.0168х2а]]]] Графики данного приближенного решения уп (х) из последнеи формулы и решения у(х), построенного с помощью Mаthemаticа 10, при а = 1;2;3 практически сливаются.
Рассматриваем еще один метод, подобньш выше тестируемым, это метод Хоина из книги [6]:
Уk+1 = y* + у [f(Xk, yk) + f X + К, yk + hf (x*, yk))]. (12)
Результаты применения метода Хоина (12) к рассматриваемой задаче (4) аналогичны результатам применения метода среднеи точки (10).
Рассмотрим тесты исправленного метода Эилера, которыи работает в соответствии с формулои:
у k+1 = у k + hk [f (Xk, y k) + \ (fX (Xk, у k) + fy (Xk, у k )f (Xk, у k))] (13)
Применение данного метода к рассматриваемои задаче (4) дает такие же результаты, как и у предыдущих методов среднеи точки (10) и Хоина (12).
Приведем результаты для стандартного решения задачи (4), полученного с помощью разложения в степеннои ряд в окрестности x0 = 0 для n = 6
yn (x) = 1 — 0.5а sinl X2 + а2 sin2 x4/12 + a3sin1 x6 (3sin21 — cos2l)/720. (14)
Заметим, что первые два слагаемых совпадают с результатом, полученным с помощью
На рис.6 видим, что во второй половине промежутка приближенное решение (14) проигрывает в точности всем приведенным выше решениям, кроме решения, полученного (5) методом Эилера для разбиения п = 2.
Результаты вычислительных экспериментов для промежутка [0,5].
Приведем результаты для значении параметра« = 1 и а=3 .
Графики приближенного решения уп (х), полученного по формуле (14), и решения у(х), построенного с помощью встроеннои операции МаШетайса 10, при а = 1 выглядят следующим образом:
Рис. 7. Графики приближённого решения уп (х) из (14) и у(х), построенного с помощью МаАетаИса 10,
при а = 1 и для ( в), г), д), е)) — п = 10
На рис.7 видим, что метод Эйлера (2) существенно проигрывает всем остальным методам, причем ситуацию не спасает значительное увеличение числа разбиении п .
Графики приближенного решения уп (х), полученного по формуле (14), и решения у(х), построенного с помощью встроеннои операции МаШетайса 10, приа = 3 выглядят следующим образом:
г) Метод средней точки (10)
д) Метод Хойна (12)
е) Исправленный метод Эйлера (13)
Рис. 8. Графики приближённого решения yn (x) из (14) и y (x), построенного с помощью Mathematica 10
при а = 3 и для ( в), г), д), е)) — n = 10 На рис.8 видим, что в данном случае лучше всего работает метод Хойна (12). По данным графикам может сложиться неверное представление о сравнительной эффективности методов: более точными представляются (2), (7), (10), (12), (13). Однако уточненныи метод Эилера (7) при n = 10 дает вполне обозримое приближение:
yn (x) = 0.02 (50 — 5х2а Sinl — 8x 2а Sin[1 — 0.02x 2а Sinl] —
— 6×2а Sin[0.04(25 — x2а Sinl — x2a Sin[-0.02×2а Sinl])] —
— 4×2аSin[0.02(50 — 3×2а Sinl — 4x2aSin [l — 0.02×2а Sinl] —
— 2×2а Sin[0.04(25 — x2а Sinl — x2aSin[l — 0.02×2а Sinl])])] —
-2x2a Sin[0.04(25 — 2×2а Sinl — 3×2а Sin[l — 0.02×2а Sinl] —2x2a Sin[0.04(25 — x2a Sinl- x2а Sin[l- 0.02×2а Sinl])] —x2aSin[0.02(50 — 3×2а Sinl — 4x2aSin [l — 0.02x2a Sinl] —
-2xa Sin[0.04(25 — x2a Sinl- x2a Sin[l- 0.02Sinl])])])]). Методы, использующие формулы (10) — метод среднеи точки, (12) — метод Хоина, (13) -исправленныи метод Эилера, дают существенно более сложные аналитические выражения.
Первым направлением развития является включение начальных условии в параметры решения. Так, например, в качестве обобщения задачи (4) получаем
í y» (x) + a sin(y) = 0,
1 y(0) = y0,y’ (0) = yl. Методом Эилера при n = 3 получаем приближенное решение
y0 + yl x — 2 x2a sin y0 -1 x2a sin
а при n = 5 — приближенное решение
y0 + y1 x — — (4x2a sin [y0 ] + 3x2asin
3 y1 x 2 2 1 2 y0 +—^—— x asin[y0]+
Аналогичные результаты можно получить, применяя и другие методы, приведенные выше. Подобные параметрические решения можно применить для решения краевых задач. Например, задачу
Г y»(x) + a sin(y) = О, 1 У(О) = Уo, У(а) = Уа ,
можно решать, определяя y1 из уравнения y(a) = ya, используя в качестве y(x) полученное параметрическое решение.
Второе направление развития связано с тем, что в формуле (2) и других аналогичных формулах используется не сама функция f (x, y), а ее неиросетевое приближение. Подобныи вариант может возникать, например, когда функция f(x, y) задана таблично или получается решением некоторои другои задачи, когда это решение целесообразно искать в классе неиросетевых функции. В результате даже для однослоиных неиросетевых функции f(x, y) получаем решение в виде многослоинои неироннои сети.
Третье направление получается при оптимизации расстановки точек xk исходя из минимизации подходящего функционала ошибки. Данное направление можно развить, заменив числовые значения в полученных выше аналитических приближенных решениях параметрами и подбирая эти параметры минимизациеи функционала ошибки, используя исходные числовые значения как начальные приближения. При использовании неироннои сети, как это было указано выше, в результате такого подхода получаем обычную процедуру обучения.
Четвёртое направление связано с распространением изложенного подхода на уравнения в частных производных. Для этого можно применить, например, метод прямых.
Работа поддержана Российским фондом фундаментальных исследований (гранты №14-01-00660 и №14-01-00733).
1. Васильев А.Н., Тархов Д.А., Шемякина Т.А. Гибридный метод построения параметрической нейросетевой модели катализатора// Современные информационные технологии и ИТ-образование, 2014. — №10. — С.476-484.
2. Васильев А.Н., Тархов Д.А., Шемякина Т.А. Модель неизотермического химического реактора на основе параметрических нейронных сетей. Гибридный метод// Современные информационные технологии и ИТ-образование, 2015. — Т.2. №11. — С.271-278.
3. Васильев А.Н., Тархов Д.А., Шемякина Т.А. Многоуровневые модели окружающей среды в мегаполисах// Современные информационные технологии и ИТ-образование, 2015. — Т. 2. № 11. — С. 267-270.
4. Васильев А.Н., Тархов Д.А., Шемякина Т.А. Мезо-уровневая нейросетевая модель загрязнения атмосферного воздуха Санкт-Петербурга по данным мониторинга// Современные информационные технологии и ИТ-образование, 2015. — Т. 2. № 11. — С. 279-283.
5. Васильев А.Н., Тархов Д.А., Шемякина Т.А. Нейросетевой подход к задачам математической физики. — СПб.: «Нестор-История», 2015. — 260 с.
6. Вержбицкий В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. -М.: Оникс 21 век, 2005. — 400 с.
7. Романова А.Г., Тархов Д.А, Шемякина Т.А. О применении нейросетевых моделей в экологии// Современные информационные технологии и ИТ-образование, 2013. — № 9. — С.534 -539.
8. Budkina E. M., Kuznetsov E. B., Lazovskaya T. V., Leonov S. S., Tarkhov D. A., Vasilyev A. N. Neural Network Technique in Boundary Value Problems for Ordinary Differential Equations // Springer International Publishing Switzerland 2016 L. Cheng et al. (Eds.): ISNN 2016, LNCS 9719. 2016. — pp. 277-283.
9. Gorbachenko V. I., Lazovskaya T. V., Tarkhov D. A., Vasilyev A. N., Zhukov M.V. Neural Network Technique in Some Inverse Problems of Mathematical Physics // Springer International Publishing Switzerland 2016 L. Cheng et al. (Eds.): ISNN 2016, LNCS 9719. 2016. — pp. 310-316.
10. Kainov N.U., Tarkhov D.A., Shemyakina T.A. Application of neural network modeling to identication and prediction problems in ecology data analysis for metallurgy and welding industry// Nonlinear Phenomena in Complex Systems, 2014. — vol. 17, 1. — pp. 57-63.
11. Lazovskaya T.V., Tarkhov D.A. Fresh approaches to the construction of parameterized neural network solutions of a stiff differential equation. St. Petersburg Polytechnical University Journal: Physics and Mathematics (2015), http://dx.doi.org/10.1016/j.spjpm.2015.07.005
12. Shemyakina T. A., Tarkhov D. A., Vasilyev A. N.// Springer International Publishing Switzerland 2016 L. Cheng et al. (Eds.): ISNN 2016, LNCS 9719. 2016. — pp. 547-554.
13. Tarkhov D., Vasilyev A. New neural network technique to the numerical solution of mathematical physics problems. I: Simple problems Optical Memory and Neural Networks (Information Optics), 2005. — 14. — pp. 59-72.
14. Tarkhov D., Vasilyev A. New neural network technique to the numerical solution of mathematical physics problems. II: Complicated and nonstandard problems Optical Memory and Neural Networks (Information Optics), 2005. — 14. — pp. 97122.
15. Vasilyev A., Tarkhov D. Mathematical Models of Complex Systems on the Basis of Artificial Neural Networks// Nonlinear Phenomena in Complex Systems, 2014. — vol. 17, 2. — pp. 327-335.
1. Vasil’ev A.N., Tarkhov D.A., Shemyakina T.A. Gibridnyy metod postroeniya parametricheskoy neyrosetevoy modeli katalizatora// Sovremennye informatsionnye tekhnologii i IT-obrazovanie, 2014. — №10. — S.476-484.
2. Vasil’ev A.N., Tarkhov D.A., Shemyakina T.A. Model’ neizotermicheskogo khimicheskogo reaktora na osnove parametricheskikh neyronnykh setey. Gibridnyy metod// Sovremennye informatsionnye tekhnologii i IT-obrazovanie,
2015. — T.2. №11. — S.271-278.
3. Vasil’ev A.N., Tarkhov D.A., Shemyakina T.A. Mnogourovnevye modeli okruzhayushchey sredy v megapolisakh// Sovremennye informatsionnye tekhnologii i IT-obrazovanie, 2015. — T. 2. № 11. — S. 267-270.
4. Vasil’ev A.N., Tarkhov D.A., Shemyakina T.A. Mezo-urovnevaya neyrosetevaya model’ zagryazneniya atmosfernogo vozdukha Sankt-Peterburga po dannym monitoringa// Sovremennye informatsionnye tekhnologii i IT-obrazovanie, 2015. — T. 2. № 11. — S. 279-283.
5. Vasil’ev A.N., Tarkhov D.A., Shemyakina T.A. Neyrosetevoy podkhod k zadacham matematicheskoy fiziki. — SPb.: «Nestor-Istoriya», 2015. — 260 s.
6. Verzhbitskiy V.M. Chislennye metody. Matematicheskiy analiz i obyknovennye differentsial’nye uravneniya. — M.: Oniks 21 vek, 2005. — 400 s.
7. Romanova A.G., Tarkhov D.A, Shemyakina T.A. O primenenii neyrosetevykh modeley v ekologii// Sovremennye informatsionnye tekhnologii i IT-obrazovanie, 2013. — № 9. — S.534 -539.
8. Budkina E. M., Kuznetsov E. B., Lazovskaya T. V., Leonov S. S., Tarkhov D. A., Vasilyev A. N. Neural Network Technique in Boundary Value Problems for Ordinary Differential Equations // Springer International Publishing Switzerland 2016 L. Cheng et al. (Eds.): ISNN 2016, LNCS 9719. 2016. — pp. 277-283.
9. Gorbachenko V. I., Lazovskaya T. V., Tarkhov D. A., Vasilyev A. N., Zhukov M.V. Neural Network Technique in Some Inverse Problems of Mathematical Physics // Springer International Publishing Switzerland 2016 L. Cheng et al. (Eds.): ISNN
2016, LNCS 9719. 2016. — pp. 310-316.
10. Kainov N.U., Tarkhov D.A., Shemyakina T.A. Application of neural network modeling to identication and prediction problems in ecology data analysis for metallurgy and welding industry// Nonlinear Phenomena in Complex Systems, 2014. — vol. 17, 1. — pp. 57-63.
11. Lazovskaya T.V., Tarkhov D.A.: Fresh approaches to the construction of parameterized neural network solutions of a stiff differential equation. St. Petersburg Polytechnical University Journal: Physics and Mathematics (2015), http://dx.doi.org/10.1016/j.spjpm.2015.07.005
12. Shemyakina T. A., Tarkhov D. A., Vasilyev A. N.// Springer International Publishing Switzerland 2016 L. Cheng et al. (Eds.): ISNN 2016, LNCS 9719. 2016. — pp. 547-554.
13. Tarkhov D., Vasilyev A. New neural network technique to the numerical solution of mathematical physics problems. I: Simple problems Optical Memory and Neural Networks (Information Optics), 2005. — 14. — pp. 59-72.
14. Tarkhov D., Vasilyev A. New neural network technique to the numerical solution of mathematical physics problems. II: Complicated and nonstandard problems Optical Memory and Neural Networks (Information Optics), 2005. — 14. — pp. 97122.
15. Vasilyev A., Tarkhov D. Mathematical Models of Complex Systems on the Basis of Artificial Neural Networks// Nonlinear Phenomena in Complex Systems, 2014. — vol. 17, 2. — pp. 327-335.
Приближенное решение обыкновенных дифференциальных уравнений. Метод Эйлера
Практическое занятие №25
«Численное интегрирование с помощью формул прямоугольников, трапеций, Симпсона.
Приближенное решение дифференциальных уравнений с помощью формул Эйлера»
1. Цель: Выработать навыки и умения по применению методов приближённого
интегрирования – формул прямоугольников, трапеций и Симпсона, в решении
приближенными методами дифференциальных уравнений
Пояснения к работе
2.1 Краткие теоретические сведения:
Формула прямоугольников
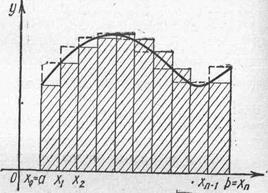
Известно, что не для всякой непрерывной функции ее первообразная выражается через элементарные функции. Кроме того, на практике сталкиваются с необходимостью вычислять интегралы от функций, заданных табличным или графическим способами, а так же интегралы от функций, первообразные которых выражаются через элементарные очень сложно, что требует большой вычислительной работы и с практической точки зрения нерационально. В этих случаях вычисление определенного интеграла по формуле Ньютона – Лейбница затруднительно, поэтому прибегают к различным методам приближенного интегрирования. Наиболее простым методом приближенного вычисления определенного интеграла является метод прямоугольников, основанный на непосредственном определении интеграла:
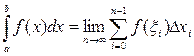
где 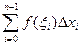
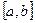
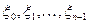
Вычисление определенного интеграла 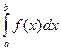
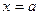
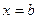
Для точности численного интегрирования нужно отрезок 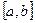

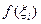
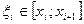
интеграла на отрезке 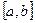
Практически удобно делить отрезок 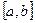
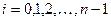
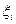
левыми 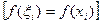
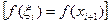
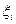
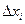
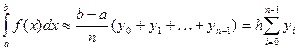
где 
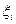
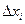

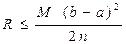
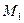
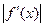
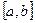
Пример 1. Используя формулу прямоугольников при 

Решение: разделим отрезок 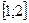
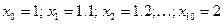

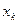 | 1 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2 |
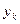 | 1.000 | 0.909 | 0.833 | 0.769 | 0.714 | 0.667 | 0.625 | 0.588 | 0.556 | 0.526 | 0.5 |
Тогда получим 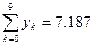
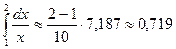
Оценим погрешность. Имеем 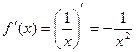
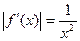
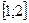
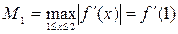

Так как допущенная погрешность влияет уже на второй знак после запятой, то третий знак следует округлить. Значит, 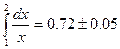
Лейбница, то получим 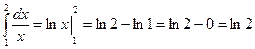
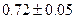

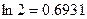
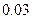
Формула трапеций
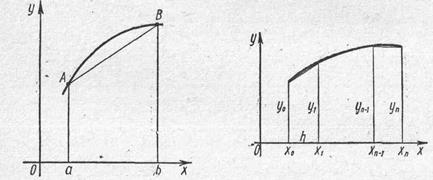
Приближенное значение определенного интеграла можно вычислить и иным способом.
Заменим на отрезке 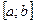
интеграла численно равным площади этой трапеции.
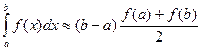
Это и есть формула трапеций для приближенного вычисления интеграла. Погрешность вычисления
для формулы трапеций оценивается так:
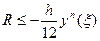
где точка 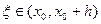
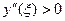
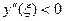
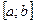
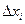
Для простоты вычислений удобно делить отрезок 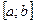
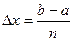
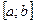
Эта формула называется общей формулой трапеций. Общую формулу трапеций можно переписать в более удобном виде:
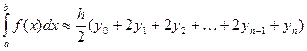

Пример 2.Вычислить интеграл 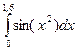
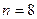
Решение: составим таблицу значений подынтегральной функции при 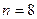
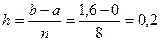
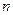 | 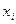 | 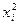  | 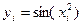 | 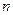 | 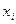 | 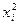 | 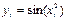 |
| 0,2 0,4 0,6 | 0,02 0,16 0,36 | 0,0000 0,0400 0,1593 0,3523 | 0, 1,0 1,2 1,4 1,6 | 0,64 1,0 1,44 1,96 2,56 | 0,5972 0,8415 0,9915 0,9249 0,5487 |
Используя формулу 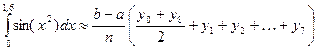
Находим:
Примечание. Если данный интеграл вычислить при 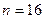
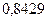
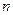
Формула Симпсона
Точность приближенного интегрирования заметно возрастает, если подынтегральную функцию 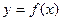
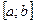
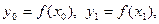
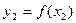
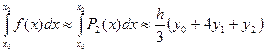
Соотношение (7) называется формулой Симпсона. Формула Симпсона обладает повышенной точностью и является точной не только для многочленов второй степени, но и третьей. Погрешность формулы Симпсона оценивается следующим образом:
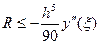
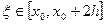
Для увеличения точности вычислений отрезок 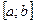
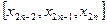
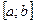
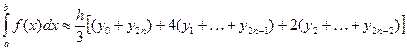
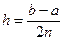
Соотношение (9) называется общей формулой Симпсона.
Пример 3. Вычислить по формуле Симпсона 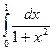
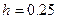
По формуле (9) имеем 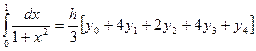
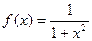
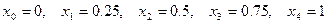
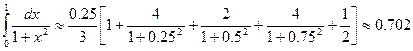
Приближенное решение обыкновенных дифференциальных уравнений. Метод Эйлера
Простейшим обыкновенным дифференциальным уравнением является уравнение первого порядка, разрешенное относительно производной:

Основная задача, связанная с этим уравнением, известна как задана Коши:найти решение уравнения (10) в виде функции у(х), удовлетворяющей начальному условию

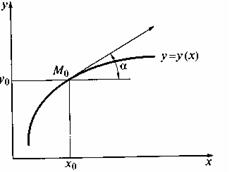
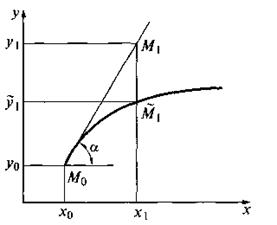
Геометрически это означает, что требуется найти интегральную кривую у = у(х), проходящую через
заданную точку M0(x0, .y0), при выполнении равенства (11) (см. рис.6). С численной точки зрения задача Коши выглядит следующим образом: требуется построить таблицу значений функции у=у(х), удовлетворяющей уравнению (10) и начальному условию (11) на отрезке [a;b]с некоторым шагом h. Обычно считается, что х0 = а, т.е. начальное условие задано в левом конце отрезка.
Простейшим из численных методов решения дифференциальных уравнений является метод Эйлера.В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.
Пусть дано уравнение (10) с начальным условием (11) (т.е. поставлена задача Коши). Решим вначале следующую задачу: найти простейшим способом приближенное значение решения в некоторой точке x1 = х0 + h, где h — достаточно малый шаг.
Заметим, что уравнение (10) совместно с начальным условием (11) задают направление касательной к искомой интегральной кривой в точке М0(х0, у0). Уравнение касательной имеет вид
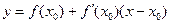
Двигаясь вдоль этой касательной (рис. 7), учитывая соотношения (10) и (12), получим приближенное значение решения в точке х1:
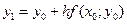
Располагая приближенным решением в точке М1 (х1,y1), можно повторить описанную ранее процедуру: построить прямую, проходящую через эту точку с угловым коэффициентом f (х1, y1) и по ней найти приближенное значение решения в точке х2 = х1 + h. Заметим, что в отличие от ситуации, изображенной на рис. 7, эта прямая не есть касательная к реальной интегральной кривой, поскольку точка M1, нам недоступна. Однако представляется интуитивно ясным, что если h достаточно мало, то получаемые приближения будут близки к точным значениям решения.
Продолжая эту идею, построим систему равноотстоящих точек
Получение таблицы значений искомой функции у(х) по методу Эйлера заключается в циклическом
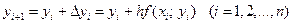
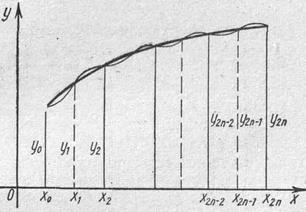
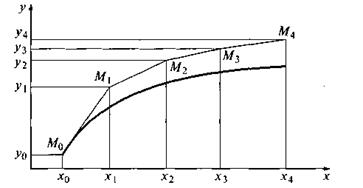
Геометрическая иллюстрация метода Эйлера приведена на рис. 8. Вместо интегральной кривой в реальности получается совокупность прямых (так называемая ломаная Эйлера).
Рис.8 Ломаная Эйлера
Методы численного интегрирования дифференциальных уравнений, в которых решение получается от одного узла к другому, называются пошаговыми. Метод Эйлера — простейший представитель семейства пошаговых методов.
Отметим, что оценка погрешности метода при таком элементарном рассмотрении невозможна даже на первом шаге. Кроме того, особенностью любого пошагового метода является то, что, начиная со второго шага исходное значение у, в формуле (13) само является приближенным, т.е. погрешность на каждом следующем шаге систематически возрастает.
Наиболее используемым эмпирическим методом оценки точности как метода Эйлера, так и других пошаговых методов приближенного численного интегрирования обыкновенных дифференциальных уравнений является способ двойного прохождения заданного отрезка — с шагом h и с шагом h/2. Совпадение соответствующих десятичных знаков в полученных двумя способами результатах дает эмпирические основание считать их верными (хотя полной уверенности в этом быть не может).
Одна из принципиальных трудностей всех пошаговых методов численного решения дифференциальных уравнений состоит в возможности столкнуться с неустойчивостью метода. Оценка погрешности неявно предполагает, что ломаная приближенного решения (см. рис. 8) хотя и не совпадает с интегральной кривой, но качественно на нее похожа. Чаще всего это именно так, но иногда (например, при неудачном выборе шага h) приближенное решение может быть качественно непохожим на точное (например, точное монотонно убывает, а приближенное монотонно возрастает).
Для эмпирического контроля того, не имеет ли места неустойчивость, следует численно интегрировать уравнение с несколькими, значительно отличающимися, значениями шага h, сравнивая качественно поведение решений.
Пример 4.Применяя метод Эйлера, составить таблицу значений решения дифференциального уравнения 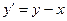
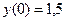
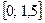
Для удобства вычислений составим таблицу.
1-й шаг: по начальным условиям заполним первую строку во 2-м и 3-м столбцах ;
2-й шаг: из уравнения 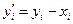
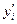
3-й шаг: содержимое столбца (4) умножаем на h (вычисляем 
записываем результат в столбец (5) этой же строки;
4-й шаг: к содержимом столбца (3) прибавляем содержимое столбца (5) этой же строки
(вычисляем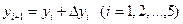
строки. Определяем хi+1 = xi + h и затем шаги 2-4 повторяем до тех пор, пока не будет пройден
весь отрезок 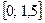
| i | xi | yi | 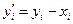 | 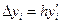 |
| (1) | (2) | (3) | (4) | (5) |
| 1,5000 | 1,5000 | 0,3750 | ||
| 0,25 | 1,8750 | 1,6250 | 0,4062 | |
| 0,50 | 2,2812 | 1,7812 | 0,4453 | |
| 0,75 | 2,7265 | 1,9765 | 0,4951 | |
| 1,00 | 3,2206 | 2,2206 | 0,5552 | |
| 1,25 | 3,7758 | 2,5258 | 0,6314 | |
| 1,50 | 4,4072 |
Пример 5. Решить методом Эйлера дифференциальное уравнение 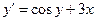
Решение: результаты вычислений с двумя знаками после запятой приведены в таблице:
| i | xi | yi | 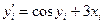 | 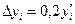 |
| (1) | (2) | (3) | (4) | (5) |
| 0,0 | 1,3 | 0,27 | 0,05 | |
| 0,2 | 1,35 | 0,82 | 0,16 | |
| 0,4 | 1,51 | 1,25 | 0,25 | |
| 0,6 | 1,76 | 1,61 | 0,32 | |
| 0,8 | 2,08 | 1,91 | 0,38 | |
| 1,0 | 2,46 |
Задание
Вариант 1
1.По формуле левых прямоугольников для n=12 вычислить значение интеграла: 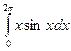
2. По формуле трапеций n=10 вычислить значение интеграла с тремя десятичными
знаками: 
3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками: 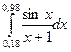
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
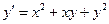
Сделайте ручную прикидку графика интегральной кривой на бумаге.
Вариант 2
1.По формуле левых прямоугольников для n=12 вычислить значение интеграла: 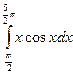
2.По формуле трапеций n=8 вычислить значение интеграла с тремя десятичными
знаками: 
3.По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками: 
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
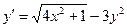
Сделайте ручную прикидку графика интегральной кривой на бумаге.
Вариант 3
1.По формуле правых прямоугольников для n=12 вычислить значение интеграла:
2.По формуле трапеций для n=10 вычислить значение интеграла с тремя десятичными
знаками:
3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками:
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
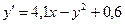
Сделайте ручную прикидку графика интегральной кривой на бумаге.
Вариант 4
1.По формуле правых прямоугольников для n=12 вычислить значение интеграла:
2. По формуле трапеций для n=10 вычислить значение интеграла с тремя десятичными знаками:
3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками:
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
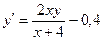
Сделайте ручную прикидку графика интегральной кривой на бумаге.
4. Контрольные вопросы:
1. Какие методы приближенного вычисления определенных интегралов вы знаете? Назовите
формулы для вычислений. Какой из них дает наиболее точный результат?
2. На чем основан метод Эйлера приближенно решения дифференциальных уравнений?
5. Содержание отчёта:
5.1 Наименование работы
5.4 Формулы для расчета
5.5 Необходимые расчеты. Анализ результатов расчетов
5.6 Выводы по работе
5.7 Ответы на контрольные вопросы
1. Колягин Ю.М. , Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах Учебное пособие — М.
Новая волна, 2005, ч.1, с.565-571;
2. Богомолов Н.В. «Практические занятия по математике» — Учебное пособие – М.:Высш. школа,
3. Лапчик М.П., Рагулина М.И., Хеннер Е.К. Элементы численных методов: учебник для студ. сред.
проф. образования -М.: Издательский центр «Академия», 2007, с.152-184
http://lektsii.org/4-22486.html