Приближенные решения уравнений методом деления отрезка

Приближенные решения уравнений методом деления отрезка

Pers.narod.ru. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений

1. Приближенное решение нелинейных алгебраических уравнений

Дано нелинейное алгебраическое уравнение

Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.

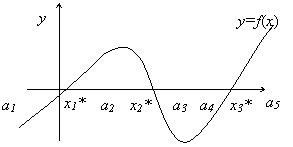
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x₁*, x₂*, x₃*, в которых функция f(x) пересекает ось x.

Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.

В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <x_n>, такой, что 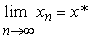. По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |x_n – x*| / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.

Если корней несколько, то для каждого нужно найти интервал изоляции.

Существуют различные способы исследования функции: аналитический, табличный, графический.

Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при 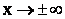и нахождение участков возрастания и убывания функции.

Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.

Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.

Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.

Найдем производную f / (x)=3x 2 -12x+3.

Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;

X₁=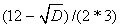= 0.268;

X₂=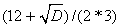= 3.732;

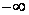
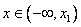
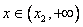
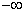
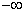
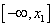
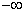
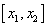
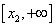
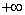
Так как f / ()>0, то f / (x)>0 при , f / (x) / (x)>0 при . Кроме того, f()= 0. Следовательно, на интервале возрастает от до f(x₁)= 3x₁ 2 -12x₁+3=11.39; на интервале — убывает до f(x₂)= 3x₂ 2 -12x₂+3=-9.39 и на интервале возрастает до , т.е. уравнение имеет три корня.

Найдем интервалы изоляции для каждого из корней.

Рассмотрим для первого корня отрезок [-2, -1]:

f(-2)= -27 0, f / (x)>0 при 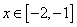т.е. этот отрезок является интервалом изоляции корня.

Рассмотрим для второго корня отрезок [1, 3]:

f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при 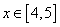т.е. этот отрезок является интервалом изоляции корня.

Приближенное вычисление корня уравнения методом деления отрезка пополам

Раздел программы: “Научно-технические расчёты на ЭВМ”

Тема урока: “Приближенное вычисление корня уравнения методом деления отрезка пополам”

Продолжительность занятия: 2 академических часа.

Тип урока: урок изучения нового материала.

Вид урока: комбинированный.

Время проведения: первый урок по теме “Приближенные вычисления”

Цели урока:

• Развитие представлений о применениях ЭВМ для научно-технических расчетов.
• Формирование системно-информационного подхода к анализу окружающего мира.
• Формирование общеучебных и общенаучных навыков работы с информацией.

Задачи урока:

• Воспитательная – развитие познавательного интереса, воспитание информационной культуры, воспитание умения четко организовать самостоятельную работу.
• Образовательная – изучить и закрепить приемы использования языка программирования для решения задач приближенного решения уравнений, закрепить знания и умения по теме “Алгоритмизация и программирование”.
• Развивающая – расширение кругозора.

Методы: Словесные, наглядные, практические.

Организационные формы работы: фронтальные, индивидуальные.

Материально-техническая база: доска, ПК с установленным ПО ЯП Turbo Pascal 7.0.

Межпредметная связь: математика.

Требования к знаниям и умениям: учащиеся должны знать основные команды языка программирования для задач вычислительного характера, уметь составлять и записывать алгоритмы с использование циклов и ветвлений; по записи алгоритма записывать программу на языке программирования Turbo Pascal.

Содержание этапа урока

Вид и формы работы1. Организационный моментПриветствие2. Мотивационное начало урока.Постановка цели урока.3 Изучение нового материала.
Ознакомление с новым методом приближенного
решения уравнений,
показ образца действий.Работа в тетради.4. Закрепление и проверка полученных знаний.Фронтальный опрос.

Работа в тетради по кодированию программ
по заданному алгоритму.5. Упражнения творческого характера.Лабораторная работа:
применение созданной программы
для приближенного вычисления корня функции.
Работа в тетради.
Защита результатов.6 Подведение итогов урока, домашнее задание.Работа в тетради.

I. Организационный момент

II. Мотивационное начало урока. Постановка цели урока

Учитель: Вычисления на компьютере обладают большей гибкостью, чем привычные всем вычисления в математике. Рассмотрим для примера задачу вычисления корня уравнения f(x) = 0. В курсе школьной математики вам известен метод дискриминанта для уравнений вида:
ax 2 + bx + c = 0, выражаемой по формуле . Однако, во многих случаях, ответ не выражается формулой (например, для корня уравнения cos(x) = x формулы просто нет). Но можно, не выводя точных формул, вычислить корень приближенно, с заданной точностью, например, до 0,0001. Сегодня мы рассмотрим один из приближенных методов вычисления корня уравнения – метод деления отрезка пополам.

III. Изучение нового материала.

Учитель: Рассмотрим задачу в следующей постановке.

Дано уравнение f(x) = 0 и числа a и b: a f(b) 0.

Если V–точный корень уравнения f(V) = 0, a * f(b) E, то перейти к пункту 1).

Любая точка отрезка [a, b] при таком алгоритме даст приближенное решение с заданной точностью.

Запишем алгоритм решения нашей задачи в виде блок схемы: (См. рис. 2).

Учитель: Есть ли вопросы?

Если у учащихся есть вопросы, то необходимо все уяснить, прежде чем переходить к следующему этапу урока/

Учитель: Какой алгоритм по структуре у нас получился?

ПО: циклический, причем использовать надо цикл с предусловием.

Учитель: Что необходимо вписать в блоки, помеченные звездочкой ( * )?

ПО: Здесь необходимо записать команду вычисления конкретной функции в точке a и в точке c.

Учитель: Что необходимо предварительно сделать, прежде чем применять этот алгоритм для нахождения корня уравнения?

ПО: Необходимо, в первую очередь, проверить, удовлетворяет ли функция постановке задачи: является ли график функции непрерывной линией на отрезке [a, b], разные ли знаки имеет функция на концах отрезка [a, b].

IV. Этап закрепления, проверки полученных знаний

Учитель: Можно ли применять метод деления отрезка пополам для нахождения корней уравнений, на заданных отрезках (уравнения записаны на доске):

1. x 2 – 5 = 0, [0, 3] (ПО: функция непрерывна на отрезке и f(0) *f(3) 4 + cos(x) – 2 = 0 [0, 2] (ПО: функция непрерывна на отрезке и f(0)*f(2) 5 – 1 = 0 [–5, 2] (ПО: функция непрерывна на отрезке и f(– 5)*f(2) e do
   Begin c : = (a + b)/2;
   fc : = … ;
   If fc . fa 2 cos(2x) + 1 = 0 [0, /2]
2. x 3 + x 2 + x + 1 = 0 [–2,1]
3. x 5 – 0,3 | x – 1 | = 0 [0,1]
4. 2x – cos(x) = 0 [0, /4]
5. tg(x) – (x + 1)/2 = 0 [0, /4]

3. Это задание для учащихся математического класса: Вычислить значения , используя этот же метод деления отрезка пополам. Ответы сравните с расчетами на инженерном калькуляторе.
ВСЕ результаты вычислений фиксируются в тетради.

4. Результаты лабораторной работы должны быть защищены в индивидуальном порядке в беседе с учителем: проверяется понимание метода и используемой программы.

Вопросы для собеседования:

1. В чем смысл переменной…?
2. Что означает данная команда…?
3. Как вы записывали для функции а) – е) выражение в команде fa : = .
4. Для чего в программе используются операторные скобки?
5. Для чего использовали в программе команду ветвления? Цикла?
6. Где в программе осуществляется выбор отрезка, где находится корень уравнения?

На выполнение задания дается 30 минут. (Для выполнения задания учащиеся рассаживаются за компьютеры, загружают среду программирования и начинают проверять программу).

Защита результатов осуществляется по мере готовности учащихся, наиболее продвинутые учащиеся назначаются консультантами и принимают зачет вместе с учителем.

VI. Подведение итогов. Домашнее задание

Учитель: Подведем итоги. Сегодня на уроке вы узнали, как находить решение уравнений методом деления отрезка пополам, как использовать для этого компьютер. Я проверила во время практической работы и в процессе защиты результатов работы как вы усвоили материал, вы хорошо справились с заданием и получили следующие отметки… На этом изучение применений компьютера для научно-технических расчетов не заканчивается, предлагаю проанализировать свои записи в тетради и выполнить домашнее задание: подумать над вопросом “Какие методы поиска площадей фигур вы знаете?”. Запишите его себе в тетрадь.
Спасибо всем за работу.

Метод деления отрезка пополам (метод бисекции)

Один из простейших методов нахождения корней нелинейных уравнений состоит в следующем. Допустим, что нам удалось найти отрезок [а, b], на котором расположено искомое значение корня (далее мы предполагаем, что х = с – единственный корень на отрезке [а, b], а если корней на [а, b] несколько, то в результате применения метода деления отрезка пополам и метода хорд (см. разд. 1.1.3) будет найдено приближенное значение одного из корней) х = с, т.е. .

В качестве начального приближения корня с0 принимаем середину этого отрезка: с0=(а+b)/2. Далее исследуем значения функции F(x) на концах отрезков [а, с0] и [с0, b], т.е. в точках а, с0, b. Тот из отрезков, на концах которого F(x) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка [a1,b1]. Вторую половину отрезка [а, b], на которой знак F(x) не меняется, отбрасываем. В качестве первого приближения корня принимаем середину нового отрезка c1 = (a1+b1)/2 и т.д. Таким образом, k-е приближение вычисляем как

(1.2)

После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после kитераций он сокращается в 2kраз:

(1.3)

Пусть приближенное решение требуется найти с точностью до некоторого заданного малого числа ε > 0:

(1.4)

Взяв в качестве приближенного решения k-еприближение корня: , запишем (1.4) с учетом обозначения — сk в виде:

(1.5)

Из (1.2) следует, что (1.5) выполнено, если

(1.6)

Таким образом, итерационный процесс нужно продолжать до тех пор, пока не будет выполнено условие (1.6).

Метод деления отрезка пополам проиллюстрирован на рис. 1.1. Пусть для определенности F(a) 0. В качестве начального приближения корня примем с0 = (а + b)/2. Поскольку в рассматриваемом случае F(c0) 0 и F(b) > 0. Таким образом, с[с0, c1],а2=с0, b2 = с1. Аналогично находим другие приближения: с2=(с0+c1)/2и т.д. до выполнения условия (1.6).

Рис. 1.1. Метод деления отрезка пополам

В отличие от большинства других итерационных методов метод деления отрезка пополам всегда сходится, причем можно гарантировать, что полученное решение будет иметь любую наперед заданную точность (разумеется, в рамках разрядности компьютера). При применении этого метода нет необходимости приближенно определять момент достижения требуемой точности, пользуясь, например, условиями близости двух последовательных приближений (2.22) или (2.23) (записанными для скалярного случая). Вместо них применяется соотношение (1.6), гарантирующее выполнение (1.4).

Однако метод деления отрезка пополам довольно медленный. Вычислим число итераций N, требуемое для достижения точности ε. Для этого выясним, пользуясь (1.3), для каких kвыполнено условие (1.6), и возьмем в качестве N наименьшее из таких k. Окончательно получим

(1.7)

где Е(х) – целая часть числа х. Обычно для метода деления отрезка пополам N больше, чем для некоторых других методов, что не является препятствием к применению этого метода, если каждое вычисление значения функции F(x) несложно.

Итерационный процесс можно завершать и тогда, когда значение функции F(x) после k-й итерации станет меньшим по модулю ε, т.е.

(1.8)

Такое условие окончания итераций аналогично условию (2.24). Действительно, для уравнения (1.1) величина F(ck)есть невязка(см. разд. 2.2.2),полученная на k—йитерации.

На рис. 1.2 представлен алгоритм итерационного процесса нахождения корня уравнения (1.1) методом деления отрезка пополам. Здесь сужение отрезка осуществляется заменой границ а или bна текущее значение корня с. При этом значение F(a) вычисляют лишь один раз, поскольку нам нужен только знак функции F(x) на левой границе, а он в процессе итераций не меняется.

Рис. 1.2. Алгоритм метода деления отрезка пополам