Приближенное нахождение корней уравнения
Задание 2 . 1) Выбрав стартовую точку с координатами x01=0.5 и xo2=0.4, примените метод Ньютона–Рафсона, и с точностью e=0.000001 найдите минимум целевой функции:
Скачать решение
2) Выбрав ту же стартовую точку, примените метод наискорейшего спуска, и вновь найдите минимум целевой функции с точностью e=0.0001.
Пример №1 . Отделить корни аналитически и уточнить один из них методом половинного деления с точностью до 0,01.
Решение.
sin(x+3.14/3)-x/2=0. Скачать
Пример №2 . Определить и найти действительные корни с точностью до 0,001: а) x 4 – 2x – 1 = 0 — методами: 1) деления отрезка пополам; 2) касательных. б) 2log(x) — (x-2) 2 = 0 — методами: 1) хорд; 2) итераций.
Решение.
Найдем корни уравнения:
x 4 -2•x-1 = 0
Используем для этого Метод половинного деления (метод дихотомии).
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Уточним интервалы, в которых будут находиться корни уравнения. Для этого исходный интервал [-1;2] разобьем на 10 подынтервалов.
h1 = -1 + 1*(2-(-1))/10 = -0.7
h2 = -1 + (1+1)*(2-(-1))/10 = -0.4
Поскольку F(-0.7)*F(-0.4) 0, то a=-0.55
Итерация 2.
Находим середину отрезка: c = (-0.55 -0.4)/2 = -0.48
F(c) = 0.000907
F(x) = 0.19
Поскольку F(c)•F(x) > 0, то a=-0.48
Итерация 3.
Находим середину отрезка: c = (-0.48 -0.4)/2 = -0.44
F(c) = -0.0884
F(x) = 0.000907
Поскольку F(c)•F(x) 0, то a=1.25
Итерация 2.
Находим середину отрезка: c = (1.25 + 1.4)/2 = 1.33
F(c) = -0.57
F(x) = -1.06
Поскольку F(c)•F(x) > 0, то a=1.33
Итерация 3.
Находим середину отрезка: c = (1.33 + 1.4)/2 = 1.36
F(c) = -0.28
F(x) = -0.57
Поскольку F(c)•F(x) > 0, то a=1.36
Итерация 4.
Находим середину отрезка: c = (1.36 + 1.4)/2 = 1.38
F(c) = -0.12
F(x) = -0.28
Поскольку F(c)•F(x) > 0, то a=1.38
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 1.25 | 1.1 | 1.4 | -1.06 | -1.06 |
| 2 | 1.33 | 1.25 | 1.4 | -0.57 | -0.57 |
| 3 | 1.36 | 1.33 | 1.4 | -0.28 | -0.28 |
| 4 | 1.38 | 1.36 | 1.4 | -0.12 | -0.12 |
| 5 | 1.39 | 1.38 | 1.4 | -0.0415 | -0.0415 |
| 6 | 1.4 | 1.39 | 1.4 | -0.000217 | -0.000217 |
| 7 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.0206 |
| 8 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.0102 |
| 9 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.00498 |
Ответ:
x = 1.4; F(x) = 0.00498
Количество итераций, N = 9
Параметр сходимости.
α = (1.4 — 1.4)/9 = 6.5E-5
Посмотрите как можно быстро решить задачу.
Приближенное вычисление корней в уравнениях
Приближенное вычисление корней в уравнениях
- Приближённое решение уравнений :
1.1 Способ хорд (или способ линейной интерполяции).
- Способ касательных (или способ Ньютона).
- Комбинированный способ (комбинированное применение способов хорд и касательных).
Приближённое решение уравнений.
Если квадратные уравнения решали уже древние греки, то способы решения алгебраических уравнений третьей и четвёртой степени были открыты лишь в XVI веке. Эти классические способы дают точные значения корней и выражают их через коэффициенты уравнения при помощи радикалов различных степеней. Однако эти способы приводят к громоздким вычислениям и поэтому имеют малую практическую ценность.
В отношении алгебраических уравнений пятой и высших степеней доказано, что в общем случае их решения не выражаются через коэффициенты при помощи радикалов. Не выражаются в радикалах, например, корни уже такого простого по виду уравнения, как:
Сказанное, однако, не означает отсутствия в науке методов решения уравнения высших степеней. Имеется много способов приближенного решения уравнений — алгебраических и неалгебраических (или, как их называют, трансцендентных), позволяющих вычислять их корни с любой, заранее заданной степенью точности, что для практических целей вполне достаточно.
На простейших из таких способов мы и остановимся, причём речь будет идти о вычислении действительных корней.
Пусть нужно решить уравнение:
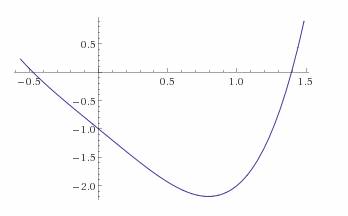
Если обратиться к рисунку, то каждый корень уравнения (1) представляет собой абсциссу точки пересечения графика функции y=f(х)
C осью Ох (рисунок №1)
С помощью графика функции или каким-нибудь иным способом обычно удаётся установить приблизительные значения корней. Это позволяет для каждого корня получить грубые приближения по недостатку и по избытку. Такого рода грубых приближений во многих случаях оказывается достаточно, чтобы, отправляясь от них, получить все значения корня с требуемой точностью. Об этом и пойдёт речь.
Итак, пусть корень Е уравнения (1) «зажат» между двумя его приближениями а и b по недостатку и по избытку а
Способ хорд (или способ линейной интерполяции).
Проведём хорду АВ (рисунок№3) и за первое приближённое значение корня примем абсциссу x1 точки С пересечения хорды с осью Ох.
Уравнение хорды имеет вид:
Поэтому в точке С:
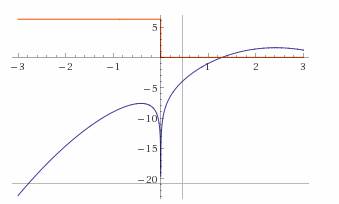
Рассмотрение всех четырёх случаев, изображённых на рисунке №2, показывает, что точка x1 лежит между a и b с той стороны от Е, где f(х) имеет знак, противоположный знаку f«(х).
Остановим внимание на первом случае: f`(х)>0, f«(х)>0 (рисунок №3), — в остальных случаях рассуждение вполне аналогично. В этом первом случае x1 лежит между a и Е. С отрезком [x1, b] поступаем так же, как мы поступаем с отрезком [a, b] (рисунок №4). При этом для нового приближённого значения корня получаем:
x1 = x2-(b- x1)*f(x1)/f(b)-f(x1)
( в формуле (2) заменяем x1 на x2, а на x1 ); значение x2 оказывается между x1 и Е. Рассматриваем отрезок [x2, b] и находим новое приближённое x3, заключённое между x2 и Е и. т. д. В результате получим последовательность а 0
Найдём первое приближённое значение корня по формуле (2):
так как f(1,588)=-0,817 0
Следовательно, искомый корень с точностью до 0,01 равен 1,64.
1.2 Способ касательных (или способ Ньютона).
В том из концов дуги АВ (рисунок №5), в котором знаки f(х) и f«(х) совпадают, проводим касательную и за первое приближённое значение корня принимаем абсциссу х1` точки Д пересечения этой касательной с осью Ох. Обратимся вновь к первому случаю, соответствующему первому рисунку №2 (f`(x)>0, f«(x)>0), — в остальных случаях рассуждают опять-таки аналогично. Уравнение интересующей нас касательной имеет вид:
и поэтому в точке Д:
Из рисунка видно, что x1` лежит между Е и b. С отрезком [a, x1`] поступаем так же, как с отрезком [a, b] ( рисунок №5), и в результате для нового приближённого значения корня получим:
х2` = x1`- f( x1`)/ f`( x1`).
Значение х2` оказывается между Е и x1`. Рассматриваем отрезок [a, х2`] и находим новое приближение х3` и т. д. В результате получим последовательность:
все более точных приближённых значений корня, причём:
xn+1`= xn`- f(xn`)/ f`( xn`) (8)
Эта формула справедлива для всех четырёх случаев, изображённых на рисунке 32. Для оценки погрешностей полученных приближений можно опять воспользоваться формулой (5), как и в первом случае, легко устанавливается сходимость последовальности x1`, х2`, х3`,…,xn`,… к значению Е
Пример №2. Методом касательных найдём положительный корень уравнения
с точностью до 0,01.
В этом уравнении f(х)=х^4-2x-4, f`(х)=4х^3-2,а f«(х)=12x^2.Так как f(х) и f«(х) при х0 = 1,7 имеют один и тот же знак, а именно:
f(1,7)=0,952>0 и f«(1,7)>0, то применяем формулу:
x1`= х0- f(х0)/ f`( х0), где f`(1,7)=4*1,7^3-2=17,652. Тогда
Применяем второй раз способ касательных:
х2= x1- f(x1)/ f` (x1), где f(x1)= f(1,646)=0,048, f` (1,646) =15,838;
f(1,643)=0,004, f` (1,643)=15,740;
Следовательно, искомый корень с точностью до 0,01 равен 1,64.
1.3 Комбинированный способ
(комбинированное применение способов хорд и касательных).
Этот способ состоит в одновременном использовании способов хорд и касательных. Остановим своё внимание опять на случае, отвечающем первому рисунку №2. Значения x1 и x1`, вычисляем по прежним формулам, т. е. принимаем:
x1`=b-f(b)/f`(b), причём: x1 0 изображён на рисунке №7. Из этого рисунка видно, что уравнение имеет положительный единственный корень, лежащий на отрезке 1 0,f«(x)>0 т. е. знак производных сохраняется. Применяем комбинированный способ:
Формулы (10) дают:
При этом x1`- x1=0,012, т. е. точность недостаточна. Совершаем второй шаг:
При этом х2`- х2=0,00018, т. е. точность достаточна. Таким образом:
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
Уравнение и его корни: определения, примеры
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6 : x = 3 .
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · ( x − 1 ) = 19 , x + 6 · ( x + 6 · ( x − 8 ) ) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · ( 8 + 1 ) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · ( x + 17 ) .
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + ( y − 6 ) 2 + ( z + 0 , 6 ) 2 = 26 .
Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня – три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня — 2 , 1 и 5 , то пишем — 2 , 1 , 5 или < - 2 , 1 , 5 >.
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых – Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как ( 3 , 4 ) .
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
http://studyport.ru/referaty/tochnyje-nauki/3800-priblizhennoe-vychislenie-kornej-v-uravnenijah
http://zaochnik.com/spravochnik/matematika/systems/uravnenie-i-ego-korni/