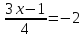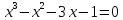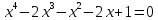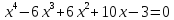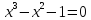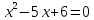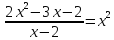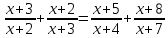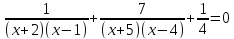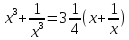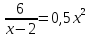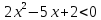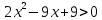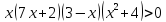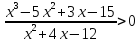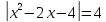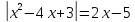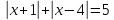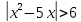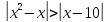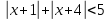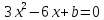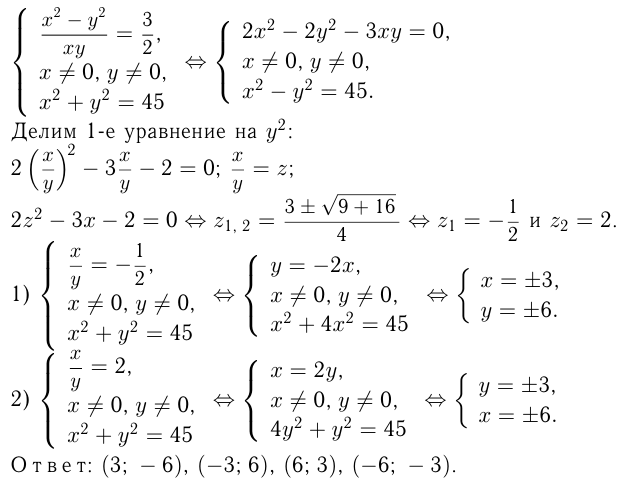Приемы решения систем уравнений и неравенств

Методы решения уравнений, неравенств и их систем

Методы решения систем уравнений с двумя переменными

1. Выражаем из какого-либо уравнения системы одну переменную через другую.
2. Подставляем вместо этой переменной полученное выражение во второе уравнение.
3. Решаем получившееся уравнение с одной переменной.
4. Находим соответствующие значения второй переменной.

Просмотр содержимого документа
«Методы решения уравнений, неравенств и их систем»

Материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики. Однако решению всех видов уравнений и неравенств уделяется недостаточно внимания. Актуальность рассмотрения данной темы обусловлена противоречием между тем, что задания, связанные с уравнениями и неравенствами и их системами регулярно встречаются в материалах ЕГЭ и ОГЭ и тем, что их решение, вызывают у учащихся значительные трудности.

Целью данной работы является: Рассмотреть методические основы профильного и углубленного обучения теме «Уравнения, неравенства и их системы».

Из данной цели вытекают задачи:

Выделить методы решения уравнений, неравенств и их систем.

Выполнить логико-дидактический анализ темы «Уравнения, неравенства и их системы» по школьным учебникам «Алгебра» Ю.Н. Макарычева за 7-9 класс и «Алгебра» А.Г. Мордковича 10-11 класс.

Разработать конспект урока по теме «Уравнения, неравенства и их системы» для 8 класса.

Данные практические разработки могут быть использованы в школе.

Данная работа состоит из трех параграфов:

§1. Методы решения уравнений, неравенств и их систем.

§2. Логико-дидактический анализ по теме «Уравнения, неравенства и их системы» по школьным учебникам «Алгебра» Ю.Н. Макарычева за 7-9 класс и «Алгебра» А.Г. Мордковича 10-11 класс.

§3. Конспект урока по теме «Уравнения, неравенства и их системы» для 8 класса.

§1. Методы решения уравнений, неравенств и их систем

Методы решения целых уравнений первой степени.

Раскрытие скобок (умножаем многочлен на многочлен). Пример: (2x+1)(3x-2)-6x(x+4)=67-2x

Домножение на НОК знаменателей дробей обеих частей уравнения. Пример: —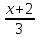

Способы решения целых уравнений.

Разложение многочлена на множители. Пример: 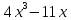+3=0

С помощью теоремы о корне многочлена. Пример:

Введение новой переменной. Пример:

Метод неопределенных коэффициентов. Пример:

Графический способ. Пример:

С помощью алгоритма решения квадратных уравнений:

Алгоритмы и способы решения дробно-рациональных уравнений.

а) Умножаем обе части уравнения на общий знаменатель дробей, входящих в уравнение.

б) Решаем полученное целое уравнение.

в) Исключаем из его корней те, которые обращают в нуль общий знаменатель дробей.

Пример:

Используя нестандартные преобразования. Пример:

Введение новой переменной. Пример:

Введение вспомогательной переменной. Пример:

Графический способ решения. Пример:

Способы решения целых неравенств с одной переменной.

1.Используя свойства дискриминанта квадратного уравнения и свойств графика квадратичной функции. Пример:

2. Метод интервалов. Пример:

3. Используя свойства графика квадратной функции. Пример:

Способы решения дробно-рациональных неравенств с одной переменной.

Разложение на множители числителя и знаменателя. Пример:

Используя систему. Примеры:

Способы решения уравнений с переменной под знаком модуля.

Замена на систему уравнений. Пример:

Замена совокупность из двух систем. Пример:

Графический способ с дальнейшей заменой на совокупность из трех систем уравнений. Пример:

Способы решения неравенств с переменной под знаком модуля.

Замена на систему неравенств. Пример:

Используя свойство модуля. Пример:

Графический способ с дальнейшей заменой на совокупность из трех систем неравенств. Пример:

Способы решения уравнений с параметром.

Вынесение многочлена за скобку. Пример: ax-2x=a 2 +a-6

Используя дискриминант. Пример:

Способы решения дробно-рациональных уравнений с параметром.

Домножение на общий знаменатель. Пример:

Методы решения систем уравнений с двумя переменными

Выражаем из какого-либо уравнения системы одну переменную через другую.

Подставляем вместо этой переменной полученное выражение во второе уравнение.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Умножаем левые и правые части уравнений.

Складываем почленно левые и правые части уравнений.

Решаем получившееся при сложении уравнение с одной переменной.

Находим соответствующие значения второй переменной.

б) Разложение на линейные множители.

Способы решения линейных неравенств с двумя переменными.

Графический. Пример: 4x-5y20

Способы решения неравенств с двумя переменными выше первой.

Способы решения системы неравенств с двумя переменными.

Способы решения неравенств с двумя переменными, содержащие знак модуля.

Методы решения уравнений высших степеней.

Используя делители свободного члена уравнения. Пример: x 3 +2x 2 -7x-12=0

Деления обеих частей уравнения на x 2 . Пример: 3x 4 -2x 3 -9x 2 -4x+12=0

Метод замены двух переменных. Пример: 2(x 2 +x+1)-7(x-1) 2 =13(x 3 -1)

Графический метод. Пример: x 5 +5x-42=0

Используя производную функции. Пример: x 4 -8x+63=0

Методы решения показательных уравнений.

Метод введения новой переменной. Пример: 4 x +2 x +1 -24=0

Методы решения показательных неравенств.

Метод уравнивания показателей. Пример:

Метод введения новой переменной. Пример:

Деления обеих частей уравнения на число с наибольшим показателем в степени. (однородные уравнения второй степени) Пример: 8 x +18 x 2∙27 x

Используя свойство дискриминанта. Пример: (x 2 +x+1) x ≤1

Методы решения логарифмических уравнений.

Введение новой переменной. Пример: lg 2 x+lg x+1=

Методы решения логарифмических неравенств.

Представление обеих частей неравенства в виде логарифмов с одинаковым основанием. Пример: (16+4x—x 2 )≤-4

Введение новой переменной. Пример:

Методы решения уравнений и неравенств с модулем.

Раскрытие модуля по определению. Пример:

Графический способ. Пример:

Используя совокупность уравнений (неравенств). Пример:

Методы решения иррациональных уравнений.

Возведение обеих частей уравнения в одну и ту же степень. Пример:

Введение новой переменной. Пример:

Уединение корня и возведение обеих частей уравнения в степень. Пример:

Введение двух новых переменных. Пример:

Умножение обеих частей уравнения на выражение сопряженное данному. Пример:

Методы решения иррациональных неравенств.

Используя совокупность неравенств. Пример:

Введение новой переменной. Пример:

Методы решения систем уравнений.

Перемножением правых и левых частей уравнения. Пример:

«Приемы решения систем уравнений и неравенств».
методическая разработка по алгебре (10 класс) по теме

Элективный курс для учащихся 10 класса.

«Приемы решения систем уравнений и неравенств».

Скачать:

Предварительный просмотр:

Элективный курс для учащихся 10 класса.

«Приемы решения систем уравнений и неравенств».

I. Уравнения n-ой степени с одним неизвестным 4-5c

Уравнения 3-ей степени 5-6с.

II.Методы решения систем линейных алгебраических 6-8с.

уравнений с несколькими неизвестными

1.Определители второго и третьего порядка.

2. Правило Крамера.

III. Системы линейных неравенств 8-13с

(на координатной плоскости)

IV.Нелинейные системы 13-15с

V.Иррациональные системы 16-17с.

8.Системы из 3-ёх уравнений с тремя неизвестными

9.Задачи на составление систем уравнений 18-20с.

Список литературы 21с.

Расширенный углубленный вариант базового курса «Решение систем уравнений и неравенств». На уроках алгебры мы рассматриваем решение линейных ,квадратных уравнений с одной переменной, систем линейных алгебраических уравнений с двумя неизвестными способом подстановки и способом почленного сложения. На ЕГЭ предлагаются задания. в которых требуется решить более сложные уравнения- уравнения третьей или четвертой степеней, системы линейных алгебраических уравнений с несколькими неизвестными, нелинейные системы, системы линейных неравенств (на координатной плоскости), иррациональные системы .

В частности к системам уравнений часто сводятся текстовые алгебраические задачи. Этот раздел алгебры считается одним из трудных, т.к. нет единых способов решения систем. Кроме того, системы, вызывают больше затруднений т.к. требуют знаний свойств уравнений, умения выполнять алгебраические преобразования, высокой логической культуры, хорошей техники исследования. И данные темы, рассмотренные на элективных занятиях расширят кругозор учащихся и помогут им в подготовке к ЕГЭ.

Цель курса : Формировать и развивать :

1. интеллектуальные, исследовательские, практические умения при помощи решения систем уравнений и неравенств;
2. умения самостоятельно приобретать и применять знания;
3. творческие способности, умения вести дискуссию.

В процессе курса учащиеся познакомятся с решением систем методом Гаусса, формулой Крамера. Научатся решать уравнения 3-ей степени.

Курс полезен для подготовки к экзаменам, для обучения на 1 курсе учебного заведения.

Курс рассчитан на 20 часов.

I. Уравнения n-ой степени с одним неизвестным -3ч.

Уравнения 3-ей степени

II.Методы решения систем линейных алгебраических

уравнений с несколькими неизвестными -4ч.

1.Определители второго и третьего порядка.

2. Правило Крамера.

III. Системы линейных неравенств -2ч.

(на координатной плоскости)

IV.Нелинейные системы -4ч

V.Иррациональные системы -3ч.

VI.Задачи на составление систем уравнений -4ч.

Основные формы работы с учащимися семинар-практикум. По каждой теме ученик сдаёт зачёт по решению каждого типа систем.

I. Уравнение n-ой степени с одним неизвестным.

Рассмотрим решение уравнений вида а n x n + a n-1 x n-1 + a n-2 x n-2 +…+a 1 x +a 0 =0, где все коэффициенты а 0 , а 1 ,а 2 . а n ,( а n ≠ 0) целые числа.

Теорема . Если все коэффициенты а 0 , а 1 ,а 2 . а n ,( а n ≠ 0) многочлена

Р n (х) =а n x n + a n-1 x n-1 + a n-2 x n-2 +…+а 1 x +a 0 =0, целые числа и рациональное число p/q

( p/q -несократимая дробь, p ЄZ, qЄN) является корнем многочлена, то коэффициент а 0 делится на p, а коэффициент а n делится q.

Док-во . Пусть рациональное число p/q( p/q -несократимая дробь, p ЄZ, qЄN) является корнем многочлена Р n (х), т.е. справедливо равенство

a n ∙ p n /q n + a n-1 ∙ p n-1 /q n -1 + … + a 1 ∙ p/q + a 0 =0.

Умножим это равенство на q n и получим a n p n + a n-1 p n-1 q +…+ a 1 pq n-1 + a 0 q n =0.

Все слагаемые в левой части этого равенства-целые числа. Их сумма. а также сумма всех слагаемых, кроме последнего, делятся на p, следовательно, последнее слагаемое a 0 q n делится на p,но тогда a 0 делится на p, т.к. q n не делится на p и числа p и q не имеют общих делителей, отличных от 1. Сумма всех слагаемых, а также, сумма всех слагаемых, кроме первого, делятся на q , следовательно, первое слагаемое a n p n делится на q,но тогда a n делится на q, т. к. p n не делится на q, ч.т.д.

Следствие . Пусть коэффициент а n многочлена с целыми коэффициентами

Р n (х) =x n + a n-1 x n-1 + a n-2 x n-2 +…+а 1 x +a 0 равен 1, тогда если этот многочлен имеет корень, то этот корень -целое число и является делителем свободного члена.

Рассмотрим решение уравнения третьей степени.

Найдем делители свободного члена: ±1, ±2, ±3, ±6.

Подберем число, при котором многочлен Р(х) = 0.

Р(1) = 1 – 6 + 11 – 6 = 0, т.е. х = 1 является корнем нашего многочлена.

Разделим многочлен на (х – 1).

х 3 – 6х 2 + 11х х – 1

х 3 – х 2 х 2 – 5х + 6

6х – 6 Решим уравнение

6х – 6 х 2 – 5х + 6 = 0 => х 1 = 2, х 2 = 3.

Ответ: х 1 = 2, х 2 = 3.х=1

2. Разложить многочлен х 3 + х 2 – х – 1 на множители .

Найдем делители свободного члена: ±1.

Подберем число, при котором многочлен Р(х)= х 3 + х 2 – х – 1 превращается в 0.

Р(1) = 1 + 1 – 1 – 1 = 0. т.е. х = 1 является корнем нашего многочлен.

Разделим Р(х) на (х – 1).

х 3 + х 2 – х – 1 х – 1

х 3 — х 2 х 2 + 2х + 1

Решим уравнение х 2 + 2х + 1 = 0 => х 1,2 = -1.

Итак, х 3 + х 2 – х – 1 = (х – 1)(х + 1) 2

3.Рассмотреть решение уравнения х 4 -4х 3 +12х-9=0

Задания для самостоятельного решения.

1. 3х 3 -2 х 2 + х – 2 = 0. х = 1.
2. 2х 3 + х 2 — 5х + 2 = 0. х = -2, х = 1, х = 1/2.
3. 3х 3 -2 х 2 — 16 х – 15 = 0. х = 3.
4. х 3 — 6х 2 + 15х — 14 = 0. х = 2.
5. х 3 + 5х 2 + 8х + 4 = 0. х = -1, х = -2.
6. х 3 + 7х 2 + 16х + 12 = 0. х = -3, х = -2.
7. х 3 — 3х — 2 = 0. х = -1, х = 2.
8. х 3 + 3х — 4 = 0. х = 1.
9. х 4 -3х 3 +6х — 4=0 х= 1, 2, , .
10. х 5 +3х 3 +2х =0 х=0

II. Системы линейных уравнений и неравенств .

1. Системы двух линейных уравнений с двумя неизвестными .

Определители второго порядка. Правило Крамера.

Рассмотрим систему двух уравнений с двумя неизвестными: а 1 х + b 1 y = c 1,

a 2 x + b 2 y = c 2.

Число  назовем определителем системы и обозначим a 1 b 1

 = = a 1 b 2 – a 2 b 1

Обозначим  х и  у – вспомогательные определители.

с 1 b 1 a 1 с 1

 х = = с 1 b 2 –с 2 b 1  у = = a 1 с 2 – a 2 с 1

с 2 b 2 a 2 с 2

Корни системы находятся по формулам: х = , у = .

Определители , х,  у, имеющие две строки и два столбца, называют определителями второго порядка .

Формулы х = , у = выражают правило Крамера для нахождения решения системы в том случае, когда   0.

Рассмотрим решение системы двух линейных уравнений с двумя неизвестными.

1. Решить систему уравнений

 = = 21 –(-10)= 31,  х = = 62,  у = = -31.

Задания для самостоятельного решения:

1). 3 4 2). 2 -3 3). 1 8 4). 0,1 -0,5

-1 2 -5 4 2 0 2 -10

 = 10  = — 7  = — 16  = 0.

1. Решить систему уравнений:

1). 3х – 4у = 7, 2). 6х + 7у = 9, 3). 9х – 11у = 1, 4). 3х – 5у = -8,

2х + 5у = -3. 5х – у = -13. 6х – 7у = 2. 7х – 4у = -2.

Ответ:(1,- 1) Ответ:(- 2, 3) Ответ:(5, 4) Ответ:(22/23, 50/23)

4.Доказать, что при любом значении а данная система имеет единственное решение, и найти это решение.

1). 3х + ау = а, 2). ах + 4у = — а,

ах – 2у = а 2 + 4. –х + 5ау = 1.

Ответ: (а, — 2). Ответ: (- 1, 0)

5.Найти все значения а и b, при которых система уравнений

а). не имеет решений; б). имеет множество решений; в). имеет единственное решение.

Ответ: а) а = — 12, b = 36. б) а = — 12, b  36. в) а  — 12.

2. Системы трех линейных уравнений с тремя неизвестными .

Определители третьего порядка.

Рассмотрим систему трех уравнений первой степени с тремя неизвестными.

а 1 х + b 1 y + c 1 z = d 1,

a 2 x + b 2 y + c 2 z = d 2,

a 3 x + b 3 y + c 3 z = d 3.

 = a 2 b 2 c 2 = a 1 b 2 c 3 + a 2 b 3 c 1 + a 3 c 2 b 1 – a 3 b 2 c 1 – b 3 c 2 a 1 – a 2 b 1 c 3

Покажем правило вычисления определителя.

а 1 b 1 c 1 а 1 b 1 c 1 а 1 b 1 c 1 а 1 b 1 c 1 а 1 b 1 c 1 а 1 b 1 с 1

a 2 b 2 c 2 a 2 b 2 c 2 a 2 b 2 c 2 a 2 b 2 c 2 a 2 b 2 c 2 a 2 b 2 с 2

a 3 b 3 c 3 a 3 b 3 c 3 a 3 b 3 c 3 a 3 b 3 c 3 a 3 b 3 c 3 a 3 b 3 с 3

d 1 b 1 c 1 а 1 d 1 c 1 а 1 b 1 d 1

 х = d 2 b 2 c 2  у = a 2 d 2 c 2  z = a 2 b 2 d 2

d 3 b 3 c 3 a 3 d 3 c 3 a 3 b 3 d 3

Корни системы находятся по формулам: х = , у = , z = при   0.

Изложенный способ решения называют правилом Крамера.

Задания для самостоятельного решения:

1. Решить систему уравнений

2 -1 3 14 -1 3 2 14 3 2 -1 14

 = 4 5 -2 = -95, х = -3 5 -2 = -190,  у = 4 -3 -2 = 95,  z = 4 5 -3 = -285

1 -6 1 11 -6 1 1 11 1 1 -6 11

х = = 2, у = = -1, z = = 3.

1). 2 3 0 2) 2 1 7 3). 2 3 5 4). 4 8 5 5). 3 -5 8 6). 1 0 -4

-1 4 5 4 2 9 1 2 4 1 -2 -3 4 8 1 3 0 5

3 1 6 6 3 11 3 8 10 5 8 2 1 5 -3 -2 6 1

 = 101  = 0  = — 8  = 0  = — 80  = — 102

1. Решить систему уравнений

1). x – 2у + 4z = 5, 2) x – y – z = -8, 3) x – 5y + 3z = — 1, 4) x – y — z = 2.

3x + 4y – z = -1, x + y – z = 4, x – y + z = 1. x – 2у — 3z = 3.

2x + y – 2z = -5. x – y + z = 6.

Ответ: (- 1, 1, 2). Ответ: (5,6,7). Ответ: (2, 0, — 1). Ответ: (0, — 3, 1).

Рассмотрим решение системы линейных алгебраических уравнений с несколькими неизвестными с помощью метода Гаусса, который заключается в том, чтобы преобразовать систему к треугольному виду.

1. Решить систему уравнений

1). х 1 – 2х 2 + х 3 – 3х 4 = 6, *-2)*-5)*-3). х 1 – 2х 2 + х 3 – 3х 4 = 6,

2х 1 – 5х 2 — 3х 3 + х 4 = — 11, – х 2 — 5х 3 + 7х 4 = -23, *2)*5)

5х 1 – 8х 2 + 6х 3 – 4х 4 = 24, 2х 2 + х 3 + 11х 4 = — 6,

3х 1 – х 2 + х 3 + 12х 4 = — 4. 5х 2 — 2х 3 + 21х 4 = — 22.

х 1 – 2х 2 + х 3 – 3х 4 = 6, х 1 – 2х 2 + х 3 – 3х 4 = 6,

– х 2 — 5х 3 + 7х 4 = -23, – х 2 — 5х 3 + 7х 4 = -23,

— 9х 3 + 25х 4 = — 52, *-3) — 9х 3 + 25х 4 = — 52,

— 27х 3 + 56х 4 = — 137. – 19х 4 = 19.

Ответ: х 4 = — 1, х 3 = 3, х 2 = 1, х 1 = 2.

2). 2х 1 – 4х 2 + х 3 – 5х 4 = 2, 3). 2х 1 – х 2 + х 3 + х 4 = 0,

4х 1 – 7х 2 — х 3 – 8х 4 = -5, х 1 – 2х 2 — х 3 – х 4 = 3,

10 х 1 – 18х 2 + 2х 3 – 23х 4 = 3, х 1 + х 2 — 2х 3 + х 4 = 5,

2х 1 – 3х 2 + х 3 – х 4 = 0. х 1 – х 2 + х 3 + 2х 4 = -1.

Ответ: (1, 2, 3, -1). Ответ: (1, 0, — 2, 0).

Задания для самостоятельного решения:

1. Решить систему уравнений

1). 7/4х – 5/3у = -1, 2). х/5 + 5у/8 = -2,

3/8х – 4/9у = -1. 8х/5 + 7у/4 = 10.

Ответ:(8, 9) Ответ:(15, — 8)

2.Найти все значения а, при которых не имеет решений система уравнений:

1). ах + 3у = а 2 + 1, 2). 2ах + у = а 2 – 2а,

(3а + 14)х + (а + 8)у = 5а 2 + 5. -10х + (а – 6)у = 10а – 5а 2 .

Ответ: а = — 6. Ответ: а = 5.

3. Решить систему уравнений

4) x + y – z = 4, 5) x — y – z = 2,

x — y + z = 6, x — y – 2z = 1,

x — y – z = — 8. x — 2y – 3z = 3.

Ответ: (5, 6, 7). Ответ: (0, — 3, 1).

6) x + y – z = 4, 7) 2x + y – z = 1,

x — y + z = -2, x — y + 2z = 4,

x — 5y + 5z = 1. 5x + 3y – 4z = 3.

Ответ: Ø . Ответ: Ø .

8) 2х – 4у + z = 3, 9) x – y – 2z = 1,

x – 5y + 3z = -1, x – y – z = 2,

x – y + z = 1. x – 2y – 3z = 3.

Ответ: (2; 0; -1), Ответ: (-1; 1; 2).

10) x – 2y + 3z = 5,

3x – 7y + 11z = 21. Ответ: Ø . 4. Системы линейных неравенств.

Рассмотрим решение линейных неравенств (на координатной плоскости).

1.Найти множество точек координатной плоскости, удовлетворяющих неравенству.

Системы уравнений и неравенств

Если какие-либо уравнения или неравенства объединены фигурной скобкой в систему, то предполагается, что они должны быть выполнены одновременно, т.е. решениями системы могут быть только такие значения неизвестных, которые удовлетворяют всем уравнениям и неравенствам, входящим в систему.

Если система уравнений или неравенств имеет решения, то говорят, что она совместна, если она решений не имеет, то — несовместна.

Системы называются равносильными, если множества их решений совпадают. Основу решения системы составляют равносильные преобразования входящих в нее уравнений и неравенств. Поскольку система включает, как правило, не одну неизвестную величину, а две, три и, возможно, больше, то для исключения неизвестных и приведения системы к уравнениям и неравенствам с одной неизвестной используют такой прием как подстановка. Если из одного уравнения можно выразить одну неизвестную через другую, а затем подставить ее в другое уравнение, то это хороший способ решения, нужно только помнить об ограничениях. Однако это нелегко сделать сразу, требуются дополнительные преобразования.

Можно складывать и вычитать уравнения системы с целью исключения одной из неизвестных. Решение системы записывается следующим образом: если в системе две неизвестных х и у, то (х; у), если три неизвестных х, у, z, то (х; у; z) и т. п. В системах, так же как и в уравнениях, используются разложение на множители, замена переменных.

Умение решать системы важно при решении текстовых задач и часто является наиболее трудоемкой частью решения.

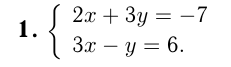
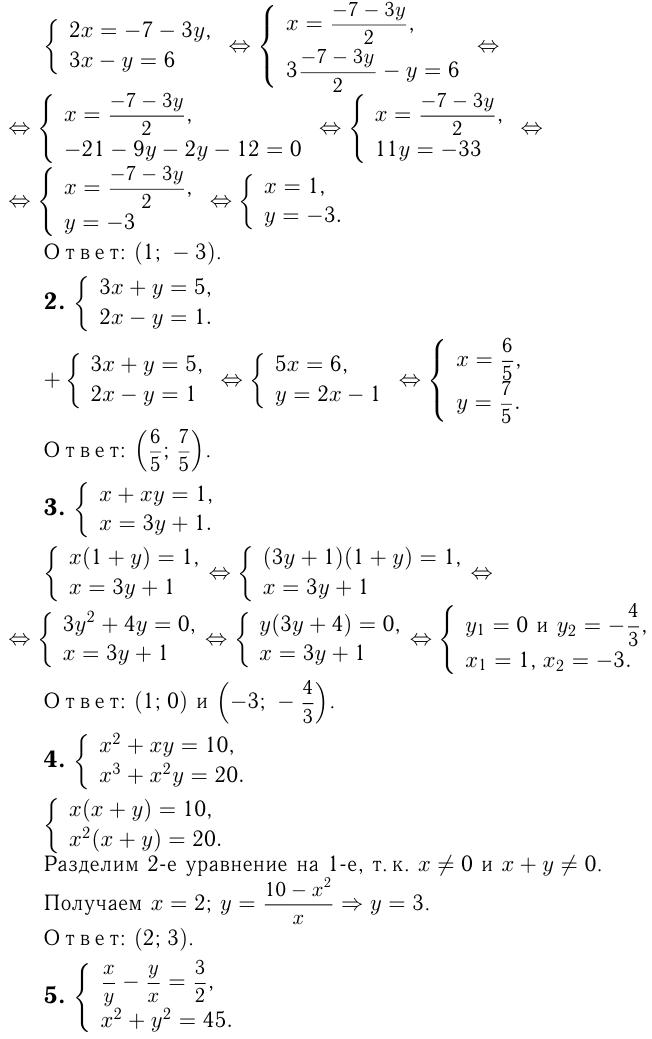
Этот материал взят со страницы решения задач по математике:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института