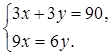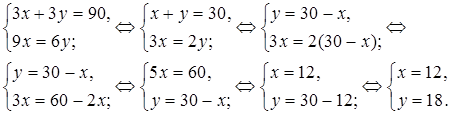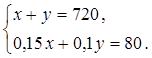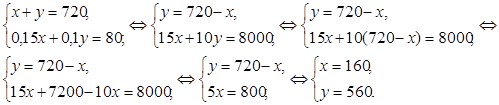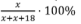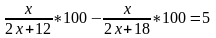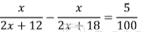Прикладная задача на составление уравнения якласс

Задачи на составление уравнений

Задачи на составление уравнений

Бригада рабочих должна была выполнить заказ за 5 дней. Ежедневно превышая норму на 18 деталей, она за 3,5 дня работы не только выполнила задание, но и изготовила 27 деталей сверх плана. Сколько деталей изготовила бригада?

В упаковке находится 2 кг смеси сухофруктов. Чернослива в этой смеси в 1,6 раза больше, чем яблок, а изюма на 0,2 кг больше, чем яблок. Сколько яблок, чернослива и изюма в упаковке в отдельности?

Каждый из двух пешеходов прошел по 6 км. Скорость первого пешехода на 3 км/ч больше скорости второго, а поэтому время, которое был в пути первый пешеход, отличается от времени второго пешехода на 1 час. Сколько времени был в пути первый пешеход?

Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от пункта А. Найдите скорость каждого, если известно, что пешеход, вышедший из А, шел со скоростью на 1км/ч большей, чем второй пешеход, и сделал в пути получасовую остановку.

Катер, собственная скорость которого 8 км/ч, прошел по реке расстояние, равное 15 км/ч, по течению и такое же расстояние против течения. Найдите скорость течения реки, если время, затраченное на весь путь, равно 4 ч.

Зарплата лаборанта составляла 100 рублей в месяц, после двух последовательных повышений на одно и то же число процентов она стала составлять 121 р. На сколько процентов каждый раз повышалась зарплата лаборанта?

За 3 м одной ткани и 3 м другой заплатили 90 рублей. Сколько стоит 1 м каждой ткани, если 9 м первой ткани стоят столько же, сколько 6 м второй ткани?

В двух корпусах пансионата было 720 мест для отдыхающих. После реконструкции в первом корпусе число мест увеличилось на 15 %, а во втором – на 10 %. Сколько мест для отдыхающих стало в каждом корпусе, если общее число мест в обоих корпусах увеличилось на 80?

Обозначим через х количество деталей, которое бригада планировала изготавливать за один день. Тогда, выполнив заказ за 5 дней, она по плану должна была изготовить 5х деталей, но превышая норму, бригада изготовляла в день (х + 18) деталей, значит, за 3,5 дня она сделала (х + 18) · 3,5 деталей. По условию задачи бригада за 3,5 дня не только выполнила задание, но и изготовила 27 деталей сверх плана. С учетом этого составляем уравнение: (х + 18) · 3,5 = 5х + 27.

Решаем полученное уравнение (х + 18) · 3,5 = 5х + 27.

5х – 3,5х = 63 – 27; 1,5х = 36; х = 24. Значит, бригада планировала изготовлять в день по 24 детали, а делала 24 + 18 = 42 детали; тогда за 3,5 дня она сделала 42 · 3,5 = 147 деталей.

О т в е т: 147 деталей.

Пусть в упаковке х кг яблок, тогда чернослива в ней 1,6х кг, а изюма – (х + 0,2) кг. Вся смесь имеет массу 2 кг.

Уравнение: х + 1,6х + х + 0,2 = 2.

Решение уравнения: 3,6х = 2 – 0,2,

В упаковке 0,5 кг яблок, 0,7 кг изюма и 0,8 кг чернослива.

О т в е т: 0,5 кг; 0,7 кг; 0,8 кг.

Пусть первый пешеход был в пути х часов, тогда 6 км он прошел за км/ч. Так как скорость первого пешехода была больше скорости второго, то второй пешеход на такое же расстояние времени затратил, по условию задачи, на 1 час больше. Значит он в пути был (х + 1) часов и его скорость была ровна км/ч.

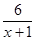
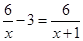
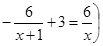
По условию задачи скорость первого пешехода была больше скорости второго пешехода на 3 км/ч. С учетом этого составляем уравнение: . (Уравнение также можно записать в виде , или .

Решаем полученное уравнение:

; ; ; ;

;

+ х – 2 = 0;

;

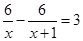
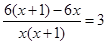
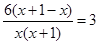
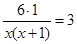
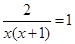
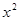
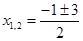
При х1 = 1 х(х+1) ? 0; при х2 = –2 х(х + 1) ? 0. значит х1 = 1 и х2 = –2 – корни уравнения, но значение х2 = –2 условию задачи не удовлетворяет, так как время движения пешехода не может быть выражено отрицательным числом. Следовательно, х = 1.

О т в е т: первый пешеход был в пути 1 час.

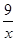
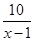
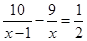
Обозначим скорость пешехода, вышедшего из пункта А, – х км/ч, тогда скорость второго пешехода – (х – 1) км/ч. Первый пешеход был в пути ч, а второй – ч. По условию задачи пешеходы вышли одновременно и встретились, но второй пешеход делал остановку на ч, следовательно, можно составить уравнение: .

Решение уравнения: Решение уравнения: 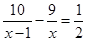, НОЗ: 2х(х – 1).

D = 9 + 4 · 18 = 91,

,

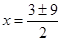
При х = 6 2х(х – 1) ? 0, при х = –3 2х(х – 1) ? 0, значит, х = 6 и х = –3 – корни составленного уравнения, но х = –3 не удовлетворяет условию задачи, остается х = 6. Скорость пешехода, вышедшего из пункта А – 6 км/ч, скорость второго 6 – 1 = 5 км/ч.

О т в е т: 6 км/ч, 5 км/ч.

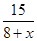
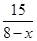
Пусть хкм/ч – скорость течения реки, тогда скорость катера по течению (8 + х) км/ч, а против течения – (8 – х) км/ч, и время движения по течению ч, а против течения ч. По условию задачи время, затраченное на весь путь, равно 4 ч.

Уравнение: .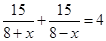

Решение уравнения: 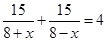;НОЗ: (8 + х)(8 – х),

При х = 2 (8 + х)(8 – х) ≠ 0, при х = –2 (8 + х)(8 – х) ≠ 0, значит х = 2 и х = –2 – корни уравнения, но х = –2 условию задачи не удовлетворяет, следовательно, х = 2, т. е. скорость течения реки 2 км/ч.

О т в е т: 2 км/ч.

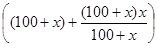
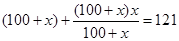
Пусть зарплата лаборанта повышалась каждый раз на х %, тогда первый раз она повысилась на 100 : 100 · х = х руб. и стала составлять (100 + х) рублей. Во второй раз она повысилась на (100 + х) : 100 · х рублей и стала составлять после этого рублей, достигнув, по условию задачи, размера 121 рубль в месяц. С учетом этого составляем уравнение: .

Решаем полученное уравнение:

;

;

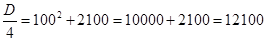
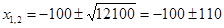
Значит, х = –210 и х = 10 – корни уравнения, но значение х = –210 условию задачи не удовлетворяет, так как является отрицательным числом. Следовательно, зарплата лаборанта дважды повышалась на 10 %.

Пусть один метр первой ткани стоит х рублей, а один метр второй ткани стоит у рублей. Тогда 3 м первой ткани стоят 3х рублей, а 3 м второй ткани стоят 3у рублей. Так как по условию задачи за 3 м одной ткани и 3 м второй заплатили 90 рублей, составляем уравнение: 3х + 3у = 90.

Поскольку 9 м первой ткани стоят 9х рублей, а 6 м второй ткани стоят 6у рублей, а по условию задачи 9 м первой ткани стоят столько же, сколько 6 м второй ткани, составляем второе уравнение: 9х = 6у.

Так как х и ув обоих уравнениях обозначают одни и те же величины, можно составить систему уравнений:

Решаем систему уравнений.

Итак, решение системы: (12; 18). Значит, 1 м первой ткани стоит 12 рублей, а 1 м второй – 18 рублей.

О т в е т: 12 р., 18 р.

Пусть в первом корпусе было х мест, а во втором у мест. Так как по условию задачи в обоих корпусах вместе было 720 мест, то можно составить уравнение: х + у = 720.

Поскольку число мест в первом корпусе увеличилось на 15 %, то есть на 0,15х мест, а во втором – на 10 %, то есть на 0,1у мест, причем общее число мест в обоих корпусах увеличилось на 80, то можно составить второе уравнение: 0,15х + 0,1у = 80.

Итак, имеем систему уравнений:

Решаем полученную систему уравнений:

Значит, в первом корпусе первоначально было 160 мест, затем стало: 160 · 1,15 = 184; во втором корпусе первоначально было 560 мест, затем стало: 560 · 1,1 = 616 мест.

О т в е т: 184 места и 616 мест.

ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

По шоссе движутся две автомашины с одной и той же скоростью. Если первая машин увеличит свою скорость на 10 км/ч, а вторая – уменьшит на 10 км/ч, то первая автомашина за 5 часов пройдет столько же, сколько вторая за 7 часов. С какой скоростью движутся автомашины?

Два токаря должны изготовить по 40 деталей. Сколько деталей в час изготавливал первый токарь, если второй, изготавливая на 3 детали в час меньше, затратил на всю работу на 3 часа больше?

Группа школьников купила мороженое, уплатив за покупку 1 р. 45 к. монетами достоинством в 10 к. и 15 к. Сколько монет по 10 к. и сколько монет по 15 к. отдали школьники за покупку, если всего было отдано 11 монет?

О т в е т: 60 км/ч.

О т в е т: 8 деталей в час.

О т в е т: 4 монеты по 10 к. и 7 монет по 15 к.

Конспект интегрированного урока для 11 класса на тему «Составление дифференциальных уравнений по условиям прикладных задач»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Общеобразовательное учреждение

средняя школа №16 г. Пинска

Интегрированный урок по физике и математике

на тему

“Составление дифференциальных уравнений

по условиям прикладных задач”

учителя: Федорино С. И.

Урок посвящен изучению темы в лицейском физико-математическом 11 классе. Он основан на групповой технологии обучения учащихся.

Цели урока:

Обучающая. Учить составлять дифференциальные уравнения по условиям прикладных задач.

Развивающая. Закрепить и углубить имеющиеся теоретические знания по темам “Дифференциальные уравнения и их классификация”. Повторить некоторые теоретические сведения из курса физики, необходимые для решения рассматриваемых задач. Создать условия для формирования навыков составления дифференциальных уравнений для решения прикладных задач.

Воспитательная. Воспитывать чувство коллективизма, товарищеской взаимовыручки, культуру межличностных отношений при групповом решении задач.

Подготовка к уроку

Подбор оборудования и заданий: высокая пробирка, заполненная водой, пластмассовые шарики; карточки-задания для работы в группах, слайды для проецирования через графопроектор.

Организация и ход урока

Содержание и характер деятельности учителей и учащихся на этапах урока.

Учитель математики : Объявляет тему урока.

Учитель физики : Объявляет цели данного урока.

Учитель математики : На предыдущих уроках мы с вами познакомились с дифференциальными уравнениями и их классификацией. Дифференциальные уравнения объединяют и обобщают многие идеи математического анализа, раскрывают сущность метода бесконечно малых величин, как важнейшего средства познания явлений действительности. Составить дифференциальное уравнение — это, значит, найти зависимость между аргументом функции, функцией и ее производной. Сегодня, как уже говорилось, мы будем учиться составлять дифференциальные уравнения по условиям физических задач.

Учитель физики : Составление дифференциальных уравнений является важнейшим и вместе с тем трудным вопросом. Универсального метода, пригодного во всех случаях, указать нельзя. Необходимо приобретение опыта и определенных навыков в решении различных задач, что достигается разбором большого количества решаемых задач и самостоятельного решения аналогичных примеров. Необходимо также знание данной прикладной дисциплины. Все задачи, которые сегодня будут разобраны на уроке, выбраны из олимпиад «Абитуриент 88 – 2000», которые предлагались на заочные туры для школьников. Многие из вас уже почувствовали необходимость данной темы при прохождении тестирования по математике и физике; при участии в олимпиадах МФТИ, БГУ и БГУИР.

Учитель математики : Для повторения и систематизации знаний проводит опрос на классификацию дифференциальных уравнений (демонстрирует карточки с заранее заготовленными уравнениями).

Учитель физики : После повторения темы совместно составим дифференцированное уравнение к конкретной физической задаче. Сложность составления дифференциального уравнения заключается еще и в переходе от математической записи (у, у’, х’, dx , dy ) к конкретным физическим величинам (х’, da , dA , q ‘, dF ). Попробуем преодолеть эту трудность.

Учитель математики : Зачитывает условие задачи: шарик массой m и радиусом R падает в вертикальном сосуде высотой Н полностью заполненный водой, встречая силу сопротивления пропорциональную скорости движения ( F_C = kV ). Найти скорость шарика и ускорение, с которым он упадёт на дно сосуда.

Учитель физики : Моделирует задачу на опыте (в пробирку с водой опускает пластмассовые шарики). Два ученика параллельно оформляют на доске «Дано», строят пояснительный чертеж, изображают действующие на шарик силы. Третий ученик записывает II закон Ньютона в век­торной форме, выбирает координатную ось и переписывает закон в скалярной фор­ме, находя проекции на выбранную ось:

Учитель математики : Озвучивает «Алгоритм составления дифференциального уравнения», ученики слушают:

Алгоритм составления дифференциального уравнения :

1. Выбирают соответствующие рассматриваемой ситуации независимую переменную и искомую функцию и вводят для них (или используют общепринятые) обозначения (например, s ( t ) — путь, пройденный телом к моменту времени t ; v ( t ) — скорость тела в момент времени t ; q ( t ) — количество зарядов, протекших через единичное сечение проводника за время t от начала процесса; у(х) — функция, графиком которой является некоторая кривая, и т.д.).

2. Определяют физическую или геометрическую интерпретацию производной искомой функции или, если надо, ее второй или, более высокой производной (например, s ‘( t ) — скорость тела в момент времени t ; s »( t ), v ‘( t ) — ускорение тела в момент времени t; q ‘( t ) — сила тока в проводнике в момент времени t ; у'(х) — угловой коэффициент к графику функции у = у(х) и т.д.).

3. Используя физический закон, описывающий рассматриваемую ситуацию, связывают производную искомой функции с самой функцией и иными параметрами системы.

4. Определяют, исходя из условий задачи, начальные условия, налагаемые на искомую функцию.

5. Приводят полученное уравнение (если это возможно) к одному из стандартных видов и формулируют для него начальную задачу.

Учитель физики : Пошагово выполняет действия по алгоритму, при этом делает записи на доске:

1) Определяем зависимость скорости шарика от времени: V = f (t), т.е. t — независимая переменная, V — искомая функция;

2) Ускорение шарика можно записать как: а = V ‘ = ;

3) По условию задачи известна длина сосуда, поэтому необходимо перейти к зависимости скорости шарика V от длины х:

= =

4) При х = 0, скорость шарика равна нулю: V = 0, при этом

m = mg – F_A – F_C

m = mg – F_A – kV

m V = mg – F_A – kV

5) Разделяя переменные, приводим полученное дифференциальное уравнение:

= dx

Учитель математики: В ознакомительном плане показывает, как решается за­дача по этапам.

Учитель физики: С помощью графопроектора показывает готовые промежуточные результаты на доске:

= dx

(–V – ln ( – V)) = x + C

(–V – ln [ ]) = x

Учитель математики : Теперь, используя алгоритм составления дифференциального уравнения, а также разобранную задачу каждая группа составит дифференциальное уравнение к конкретной физической задаче (Приложение: “Задачи для работы в группах”). Класс заранее разбит на 6 групп по 4 – 5 человек по принципу дифференциации. Задачи лежат на заранее сдвинутых партах. На каждую парту ставятся бумажные треугольники, на гранях которых написано:

— номер группы (соответствует номеру решаемой задачи),

— сигнал о возникновении зат­руднения при совместном решении;

— сигнал о готовности решения.

Учащиеся знакомятся с условием задачи, распределяют обязанности внутри группы, намечают пути решения данной задачи.

Учитель физики: Засекает время, включает негромкую инструментальную мелодию.

Ученики : 6 человек (по одному представителю от каждой группы) офор­мляют на доске свои решения. При этом придерживаются схемы:

— закон или функция;

— классификация дифференциального уравнения.

Учитель математики : подводит итог урока.

Учитель физики: задает домашнее задание (оставшиеся 4 задачи).

Рефлексию урока организуют оба учителя.

ЗАДАЧА

Шарик массой m и радиусом R падает в вертикальном сосуде высотой Н полностью заполненный водой, встречая силу сопротивления пропорциональную скорости движения ( F_C = kV ). Найти скорость шарика и ускорение, с которым он упадёт на дно сосуда.

ЗАДАЧИ ДЛЯ РАБОТЫ В ГРУППАХ

1. Лыжник спускается по длинному склону с углом наклона i , не отталкиваясь палками. Коэффициент трения лыжника о снег равен μ. Сила сопротивления воздуха пропорциональна квадрату скорости (F_С = kV 2 ), где k — постоянный коэффициент. Какую максимальную скорость мог развить лыжник, если его масса m ?

2. Гибкий тяжелый трос длиной L и массой M перекинут через блок, масса и радиус которого пренебрежительно малы. Трение в блоке отсутствует. Трос находится в равновесии. К одному из концов троса подвешивают груз массой m . Найти скорость троса в момент отрыва от блока.

3. Для выработки залежи полезных ископаемых необходимо вырыть котлован площадью сечения S и глубиной Н. Найти работу А, которую необходимо выполнить, чтобы поднять породу с глубины. Плотность породы изменяется по закону: ρ = ρ₀ + by , где ρ₀ — плотность породы на поверхности, b — некоторая постоянная.

4. Водород расширяется при постоянной температуре от своего первоначального объема V ₀ имея первоначальное давление Р₀, при некотором внешнем давлении бесконечно мало отличающимся от давления газа. Найти произведенную работу водорода.

5. Моторная лодка движется в стоячей воде со скоростью V₀. На полном ходу ее мотор выключается и через время t ₁ скорость уменьшается до V ₁ . Сопротивление воды пропорционально скорости движения лодки. Определить скорость лодки через время t после остановки мотора.

6. К горизонтальной пружине, силой тяжести которой можно пренебречь, прикреплен груз массой m . Оттянув груз на длину х, его заставляют свободно колебаться. Найти закон этого движения, пренебрегая побочными сопротивлениями.

7. Пуля входит в брус толщиной 12 см со скоростью 200 м/с, а вылетает со скоростью 60 м/с. Брус сопротивляется движению пули с силой, пропорциональной квадрату скорости движения. Найти время движения пули через брус.

8. Тело массой m падает с некоторой высоты со скоростью V. При падении на него действует сила сопротивления F _С = aV 2 . Найти закон падающего тела.

9. Сила тяжести летчика с парашютом 80 кг. Сопротивление воздуха при спуске пропорционально квадрату скорости (k = 400 Нс 2 /м 2 ). Определить скорость спуска в зависимости от времени и установить максимальную скорость спуска.

10.Конденсатор емкостью С включен в цепь с напряжением U и сопротивлением R, Определить заряд q конденсатора в момент времени Т после замыкания цепи.

1. F_TP N

F_C

mg

2.

L – x

a x

3 .

dx

dmg

F_A

5. Þ ma = – F_C F_C

Þ

6. N

F _У

mg

«Решение прикладных задач с помощью системы уравнений с двумя переменными.»

Цель урока: научиться решать задачи с процентами на сплавы и смеси с помощью составления системы уравнений, а также научиться составлять к задаче математическую модель.

Просмотр содержимого документа
««Решение прикладных задач с помощью системы уравнений с двумя переменными.»»

Учитель: Коровкина Надежда Михайловна

Тема урока: «Решение прикладных задач с помощью системы уравнений с двумя переменными.»

Тип урока: Урок закрепления изученного материала.

Цель урока: научиться решать задачи с процентами на сплавы и смеси с помощью составления системы уравнений, а также научиться составлять к задаче математическую модель.

Сегодня мы будем учиться составлять математические модели к задачам на смеси и сплавы.

Рассмотрим 2 способа составления математической модели:

описательный и с помощью таблицы.

Работа с учебником. Решаем задачи №540, 546

Рассмотрим решение и оформление задачи № 540

1 способ (описательный). Давайте разберемся.

? О чем идет речь в задаче? (ответы учащихся)

Предполагаемые ответы учащихся

Какой жизненный процесс описан в задаче?

Это задача на «смеси»

Какими основными величинами характеризуется этот процесс?

Масса и процентная концентрация

Какие ситуации описаны в задаче?

30% раствор солякой кислоты

10%раствор соляной кислоты

800г нового раствора с 15% содержанием соляной кислоты

(получен при смешивании 1 и 2 растворов)

Что известно о массах растворов?

Ничего. Принимаем за неизвестное, т.е за х и у.

Вспомните , пожалуйста, из химии или из математики , как найти массу вещества в растворе? ( m_р* %, т.е сначала мы проценты переводим в дробь и умножаем массу раствора на эту дробь)

30% = 0,3 10% = 0,1 15%=0,15

Составим математическую модель задачи

1 способ (описательный)

2 способ ( с помощью таблицы)

уравнений: х + у = 800

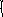
0,3 х + 0,1у = 0,15*800

Проводим анализ полученных результатов и записываем ответ.

Рассмотрим решение задачи №546 из учебника.

? Читаем задачу. О чем идет речь в задаче? …

В чем отличие от предыдущей задачи?

В отличии от предыдущей задачи здесь в сплаве содержатся 2 вещества- медь и цинк. Причем известно, что одного вещества больше, чем другого.

? Вспомните, пожалуйста, как найти процентное содержание вещества в сплаве? (Массу вещества поделить на общую массу раствора или сплава и умножить на 100%).

Составим математическую модель 1 способом (описательным) .

2 способ (в виде таблицы)

Проводим анализ полученных результатов и записываем ответ.

? Для чего нам нужно такое подробное описание задачи?

Объясняю: при подготовке к ОГЭ вы уже видели и знаете, что в №22 предлагается для решения именно задача прикладного характера, причем необходимо не просто ее решить в виде какого-то действия, а нужно привести полное подробное решение данной задачи. Только в этом случае она будет оценена в 2 балла. Вот для этого мы и учимся составлять математические модели задач.

Обучающая самостоятельная работа.

В качестве закрепления материала я предлагаю вам самим решить задачи №541, 547 (желательно разными способами)

Результат вашего решения прошу выслать мне на электронную почту в срок до 13.04.20

Если возникнут затруднения пишите! Желаю удачи!

А.Г. Мерзляк , В.Б.Полонский и др .Учебник алгебры 9 класс п. 15