уравнение множественной регрессии в натуральном и стандартизированном виде
Оценка параметров уравнения регресии в стандартизованном масштабе
Параметры уравнения множественной регрессии в задачах по эконометрике оценивают аналогично парной регрессии, методом наименьших квадратов (МНК). При применении этого метода строится система нормальных уравнений, решение которой и позволяет получать оценки параметров регрессии.
При определении параметров уравнения множественной регрессии на основе матрицы парных коэффициентов корреляции строим уравнение регрессии в стандартизованном масштабе:
в уравнении стандартизированные переменные
Применяя метод МНК к моделям множественной регрессии в стандартизованном масштабе, после опрделенных преобразований получим систему нормальных уравнений вида
Решая системы методом определителей, находим параметры — стандартизованные коэффициенты регрессии (бета — коэффициенты). Сравнивая коэффициенты друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом заключается основное достоинство стандартизованных коэффициентов в отличие от обычных коэффициентов регрессии, которые несравнимы между собой.
В парной зависимости стандартизованный коэффициент регрессии связан с соответствующим коэфициентом уравнения зависимостью
Это позволяет от уравнения в стандартизованном масштабе переходить к регрессионному уравнению в натуральном масштабе переменных:
Параметр а определяется из следующего уравнения
Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответствующий фактор xj изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все перемеyные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии сравнимы между собой.
Рассмотренный смысл стандартизованных коэффициентов позволяет использовать их при отсеве факторов, исключая из модели факторы с наименьшим значением.
Компьютерные программы построения уравнения множественной регрессии позволяют получать либо только уравнение регрессии для исходных данных и уравнение регрессии в стандартизованном масштабе.
19. Характеристика эластичности по модели множественной регрессии. СТР 132-136
20. Взаимосвязь стандартизированных коэффициентов регрессии и коэффициентов эластичности. СТР 120-124
21. Показатели множественной и частной корреляции. Их роль при построении эконометрических моделей
Корреляция—это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой Корреляции двух случайных величин служит коэффициент Корреляции. Понятие корреляции появилось в середине XIX века в работах английских статистиков Ф. Гальтона и К. Пирсона.
Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором факторных показателей:
где σ 2 — общая дисперсия эмпирического ряда, характеризующая общую вариацию результативного показателя (у) за счет факторов;
σост 2 — остаточная дисперсия в ряду у, отражающая влияния всех факторов, кроме х;
у — среднее значение результативного показателя, вычисленное по исходным наблюдениям;
s — среднее значение результативного показателя, вычисленное по уравнению регрессии.
Коэффициент множественной корреляции принимает только положительные значения в пределах от 0 до 1. Чем ближе значение коэффициента к 1, тем больше теснота связи. И, наоборот, чем ближе к 0, тем зависимость меньше. При значении R 0,6 говорят о наличии существенной связи.
Квадрат коэффициента множественной корреляции называется коэффициентом детерминации (D): D = R 2 . Коэффициент детерминации показывает, какая доля вариации результативного показателя связана с вариацией факторных показателей. В основе расчета коэффициента детерминации и коэффициента множественной корреляции лежит правило сложения дисперсий, согласно которому общая дисперсия (σ 2 ) равна сумме межгрупповой дисперсии (δ 2 ) и средней из групповых дисперсий σi 2 ):
Межгрупповая дисперсия характеризует колеблемость результативного показателя за счет изучаемого фактора, а средняя из групповых дисперсий отражает колеблемость результативного показателя за счет всех прочих факторов, кроме изучаемого.
Показатели частной корреляции. Основаны на соотношении сокращения остаточной вариации за счет дополнительно включенного в модель фактора к остаточной вариации до включения в модель соответствующего фактора
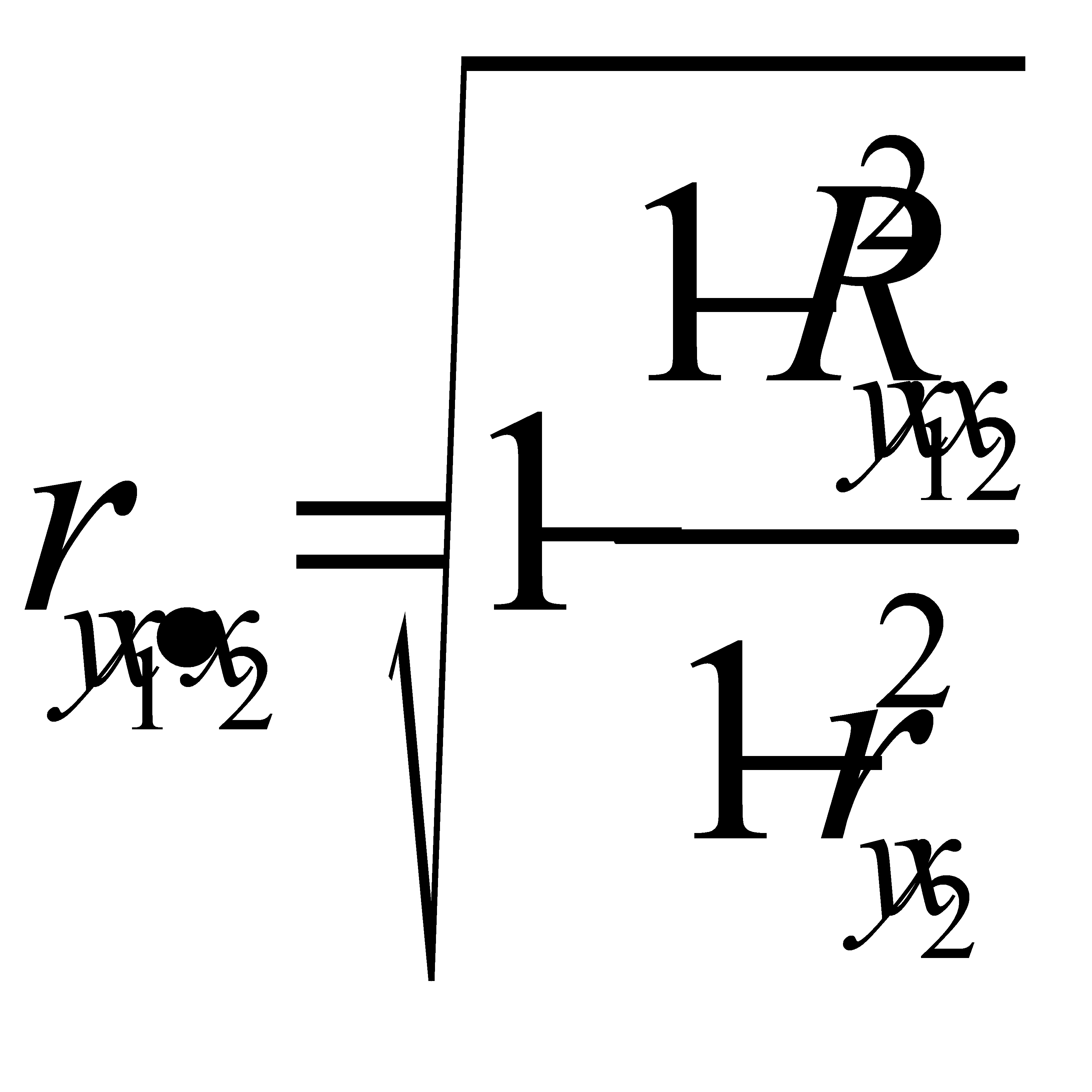
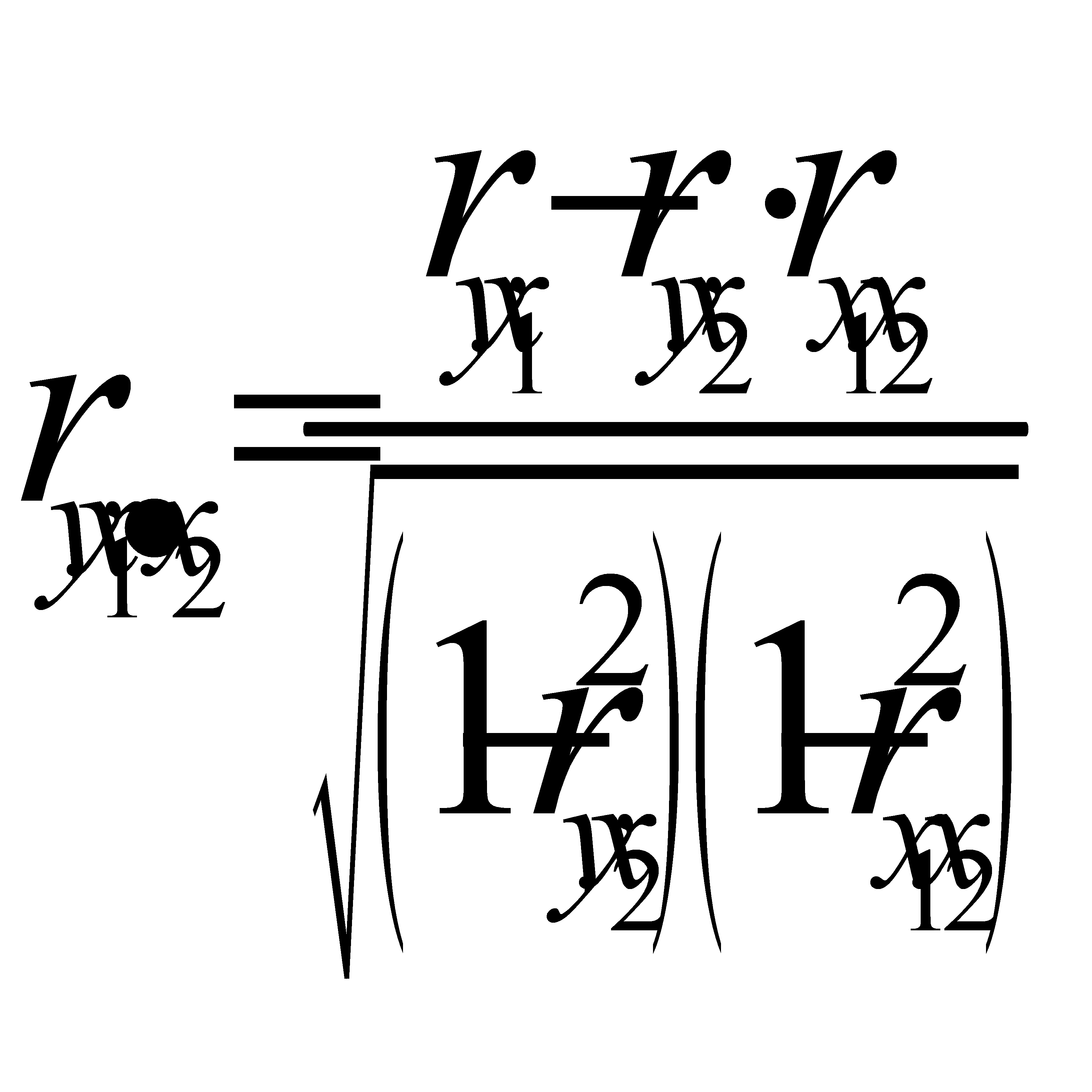

Рассмотренные показатели можно также использовать для сравнения факторов, т.е. Можно ранжировать факторы(т.е.2ой фактор более тесно связан).
Частные коэффициенты могут быть использованы в процедуре отсева факторов при построении модели.
Рассмотренные выше показатели являются коэф-ми корреляции первого порядка,т.е.они характризуют связь между двумя факторами при закреплении одного фактора (yx1.x2). Однако можно построить коэф-ты 2го и более порядка (yx1.x2x3, yx1.x2x3x4).
22. Оценка надежности результатов множественной регрессии.
Коэфициенты структурной модели могут быть оценены разными способами в зависимости от вида одновренных уравнений.
Методы оценивания коэф-тов структурной модели:
1) Косвенный МНК(КМНК)
4)МНП с полной информацией
5)МНП при огранич. информации
КМНК применяется в случаеточнойидентификацииструктурноймодели.
Процедуры примения КМНК:
1. Структурн. модель преобраз. в привед. форму модели.
2. Для каждого уравнения привед.форма модели обычным МНК оцениваются привед. коэф
3. Коэфициенты приведенной формы модели трансформируются в параметры структурной модели.
Еслиси стема сверхидентифицируема, то КМНК не исп, так как не дает однозначных оценок для параметров структурной модели. В этом случае могут исп. разные методы оценивания, среди которых наиболее распространен ДМНК.
Основная идея ДМНК на основе приведенной модели получить для сверхидентиф. уравнения теор. значения эндогенных переменных, содерж. в правой части ур-ния. Далее подставив в найденные значения вместо факт.значений применяется обычный МНК и структурн. форма сверхидент. ур-ния.
1 шаг: при опред.привед. формы модели и нахождении на ее основе оценок теор. значений эндогенной переменой
2 шаг: Применительно к структурному сверхидентифицируемому уравнению при определении структурных коэфициентов модели по данным теоритических значений эндогенных переменных.
23. Дисперсионный анализ результатов множественной регрессии.

| таблица дисперсионного анализа | ||||
| Вару | df | СКО,S | Дисп на одну df,S 2 | Fфакт |
 общ общ | n-1 | dy 2 * n | — | — |
| факт | m | dy 2 * n*R 2 yx1x2 | 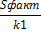 |  |
| Ост | n-m-1 | dy 2 * n*(1-R 2 yx1x2) =Sобщ-Sфакт | 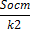 | — |
Также можно построить таблицу частного дисперсионного анализа, и найти частный F крит который оценивает целесообразность включения фактора в модель после включения др переменной
| Вариация у | df | S | S^2 |
| общая | df=n-1 | d 2 у*n | — |
| факторная | k1=m | d 2 у*n*R 2 | Sфакт/k1 |
| в том числе: | |||
| за счет x2 | d 2 у*n*r 2 yx2 | Sфактx2/1 | |
| за счет доп включ. х1 | Sфакт-Sфактх2 | Sфактx1/1 | |
| Остаточная | k2=n-m | Sобщ-Sфакт |
24. Частный F-критерий Фишера, t- критерий Стьюдента. Их роль в построении регрессионных моделей.
Для оценки статистич целесообразности добавления нов факторов в регрессион модель исп-ся частн критерий Фишера, т.к на рез-ты регрессион анализа влияет не только состав факторов, но и последовательность включения фактора в модель. Это обьясняется наличием связи между факторами.
Fxj =( (R 2 по yx1x2. xm – R 2 по yx1x2…xj-1,хj+1…xm)/(1- R 2 по yx1x2. xm) )*( (n-m-1)/1)
Fтабл (альфа,1, n-m-1) Fxj больше Fтабл – фактор xj целесообразно лючать в модель после др.факторов.
Если рассматривается уравнение y=a+b1x1+b2+b3x3+e, то определяются последовательно F-критерий для уравнения с одним фактором х1, далее F- критерий для дополнительного включения в модель фактора х2, т. е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, F-критерий для дополнительного включения в модель фактора х3, т.е. дается оценка значимости фактора х3 после включения в модель факторов x1 их2. В этом случае F-критерий для дополнительного включения фактора х2 после х1 является последовательным в отличие от F-критерия для дополнительного включения в модель фактора х3, который является частным F- критерием, ибо оценивает значимость фактора в предположении, что он включен в модель последним. С t-критерием Стьюдента связан именно частный F- критерий. Последовательный F-критерий может интересовать исследователя настадии формирования модели. Для уравнения y=a+b1x1+b2+b3x3+e оценка значимости коэффициентов регрессии Ь1,Ь2,,b3 предполагает расчет трех межфакторных коэффициентов детерминации.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдентаи доверительные интервалыкаждого из показателей.




Если t табл. tфакт. то гипотеза H0 не отклоняется и признается случайная природа формирования a, b или rху.
25. Оценка качества регрессионных моделей. Стандартная ошибка линии регрессии.
Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения 



Если это так, то большая часть вариации 
Долю общей дисперсии 
Разность 
Нет формального теста для оценки 
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования 

Мы предсказываем среднюю величину 

Итак, если 



Повторение этой процедуры для различных величин 
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования 

Мы предсказываем среднюю величину 

Итак, если 



Повторение этой процедуры для различных величин 
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
26. Взаимосвязь частного F-критерия, t- критерия Стьюдента и частного коэффициента корреляции.
Ввиду корреляции м/у факторами значимость одного и того же фактора м/б различной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частый F-критерий, т.е. Fxi. В общем виде для фактора xi частый F-критерий определяется как :
Если рассматривается уравнение y=a+b1x1+b2+b3x3+e, то определяются последовательно F-критерий для уравнения с одним фактором х1, далее F-критерий для дополнительного включения в модель фактора х2, т. е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, F-критерий для дополнительного включения в модель фактора х3, т. е. дается оценка значимости фактора х3 после включения в модель факторов x1 их2. В этом случае F-критерий для дополнительного включения фактора х2 после х1является последовательнымв отличие от F-критерия для дополнительного включения в модель фактора х3, который является частнымF-критерием, ибо оценивает значимость фактора в предположении, что он включен в модель последним. С t-критерием Стьюдента связан именно частный F-критерий. Последовательный F-критерий может интересовать исследователя на стадии формирования модели. Для уравнения y=a+b1x1+b2+b3x3+e оценка значимости коэффициентов регрессии Ь1,Ь2,,b3 предполагает расчет трех межфакторных коэффициентов детерминации, а именно: 



27. Варианты построения регрессионной модели. Их краткая характеристика.
28. Интерпретация параметров линейной и нелинейной регрессии.
| b | a | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| парная | линейная | Коэффициент регрессии b показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе – обратная | не интерпретируется, только знак >0 – рез-т изменяется медленнее фактора, * предполагают наличие положительной или отрицательной автокорреляции в остатках. Затем по спец. таблицам определяютсякритические значения критерия Дарбина — Уотсона dL и du для заданного числа наблюдений n, числа независимых переменных модели k при уровня значимости ɑ (обычно 0,95). По этим значениям промежуток [0;4] разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью (1-ɑ) представлено на след: рисунке:
Если фактич. значение критерия Дарбина — Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и гипотезу Н0 отклоняют. 34. Выбор наилучшего варианта модели регрессии. 35. Нелинейные модели множественной регрессии, их общая характеристика. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы Различают два класса нелинейных регрессий: • регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; • регрессии, нелинейные по оцениваемым параметрам.
К нелинейным регрессиям по оцениваемым параметрам относятся функции: 36. Модели гиперболического типа. Кривые Энгеля, кривая Филипса, и другие примеры использования моделей данного типа. Кривые Энгеля (Engel curve) иллюстрируют зависимость между объемом потребления благ (C) и доходом потребителя (I) при неизменных ценах и предпочтениях. Названа в честь немецкого статистика Эрнста Энгеля, занимавшегося анализом влияния изменения дохода на структуру потребительских расходов.
На оси абсцисс откладывается уровень дохода потребителя, а на оси ординат — расходы на потребление данного блага. На графике показан примерный вид кривых Энгеля:
Кривая филипса отражает взаимосвязь между темпами инфляции ибезработицы. Кейнсианская модель экономики показывает, что в экономике может возникнуть либо безработица (вызванная спадом производства, следовательно уменьшением спроса на рабочую силу), либо инфляция (если экономика функционирует в состоянии полной занятости). Одновременно высокая инфляция и высокая безработица существовать не могут. Кривая Филипса была построена А.У. Филлипсом на основе данных заработной платы и безработицы в Великобритании за 1861-1957 годы. Следуя кривой Филлипса государство может выстроить свою экономическую политику. Государство с помощью стимулирования совокупного спроса может увеличить инфляцию и снизить безработицу и наоборот. Кривая Филипса была полностью верна до середины 70х годов. В этот период случилась стагнация (одновременный рост инфляции и безработицы), которую кривая филипса не смогла объяснить. Множественная линейная регрессия. Улучшение модели регрессииПонятие множественной линейной регрессииМножественная линейная регрессия — выраженная в виде прямой зависимость среднего значения величины Y от двух или более других величин X 1 , X 2 , . X m . Величину Y принято называть зависимой или результирующей переменной, а величины X 1 , X 2 , . X m — независимыми или объясняющими переменными. В случае множественной линейной регрессии зависимость результирующей переменной одновременно от нескольких объясняющих переменных описывает уравнение или модель
где Функция множественной линейной регрессии для выборки имеет следующий вид:
где Уравнение множественной линейной регрессии и метод наименьших квадратовКоэффициенты модели множественной линейной регресии, так же, как и для парной линейной регрессии, находят при помощи метода наименьших квадратов. Разумеется, мы будем изучать построение модели множественной регрессии и её оценивание с использованием программных средств. Но на экзамене часто требуется привести формулы МНК-оценки (то есть оценки по методу наименьших квадратов) коэффициентов уравнения множественной линейной регрессии в скалярном и в матричном видах. МНК-оценка коэффиентов уравнения множественной регрессии в скалярном видеМетод наименьших квадратов позволяет найти такие значения коэффициентов, что сумма квадратов отклонений будет минимальной. Для нахождения коэффициентов решается система нормальных уравнений Решение системы можно получить, например, методом Крамера:
Определитель системы записывается так: МНК-оценка коэффиентов уравнения множественной регрессии в матричном видеДанные наблюдений и коэффициенты уравнения множественной регрессии можно представить в виде следующих матриц: Формула коэффициентов множественной линейной регрессии в матричном виде следующая:
где Решая это уравнение, мы получим матрицу-столбец b, элементы которой и есть коэффициенты уравнения множественной линейной регрессии, для нахождения которых и был изобретён метод наименьших квадратов. Построение наилучшей (наиболее качественной) модели множественной линейной регрессииПусть при обработке данных некоторой выборки в пакете программных средств STATISTICA получена первоначальная модель множественной линейной регрессии. Предстоит проанализировать полученную модель и в случае необходимости улучшить её. Качество модели множественной линейной регрессии оценивается по тем же показателям качества, что и в случае модели парной линейной регрессии: коэффициент детерминации Важный показатель качества модели линейной регрессии — проверка на выполнение требований Гаусса-Маркова к остаткам. В качественной модели линейной регрессии выполняются все условия Гаусса-Маркова:
В случае выполнения требований Гаусса-Маркова оценка коэффициентов модели, полученная методом наименьших квадратов является Затем необходимо провести анализ значимости отдельных переменных модели множественной линейной регрессии с помощью критерия Стьюдента. В случае наличия резко выделяющихся наблюдений (выбросов) нужно последовательно по одному исключить их из модели и проанализировать наличие незначимых переменных в модели и, в случае необходимости исключить их из модели по одному. В исследованиях поведения человека, как и во многих других, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы. Кроме того, требуется на основе тех же данных построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных. Они также будут сравниваться с линейными моделями, полученных на разных шагах. Также требуется построить модели с применением пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE). Все полученные модели множественной регрессии нужно сравнить и выбрать из них наилучшую (наиболее качественную). Теперь разберём перечисленные выше шаги последовательно и на примере. Оценка качества модели множественной линейной регрессии в целомПример. Задание 1. Получено следующее уравнение множественной линейной регрессии: и следующие показатели качества описываемой этим уравнением модели:
Сделать вывод о качестве модели в целом. Ответ. По всем показателям модель некачественная. Значение Для анализа на выполнение условий Гаусса-Маркова воспользуемся диаграммой рассеивания наблюдений (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши): Результаты проверки графика показывают: условие равенства нулю математического ожидания остатков выполняется, а условие на постоянство дисперсии — не выполняется. Достаточно невыполнения хотя бы одного условия Гаусса-Маркова, чтобы заключить, что оценка коэффициентов модели линейной регрессии не является несмещённой, эффективной и состоятельной. Анализ значимости коэффициентов модели множественной линейной регрессииС помощью критерия Стьюдента проверяется гипотеза о том, что соответствующий коэффициент незначимо отличается от нуля, и соответственно, переменная при этом коэффициенте имеет незначимое влияние на зависимую переменную. В свою очередь, в колонке p-level выводится вероятность того, что основная гипотеза будет принята. Если значение p-level больше уровня значимости α, то основная гипотеза принимается, иначе – отвергается. В нашем примере установлен уровень значимости α=0,05. Пример. Задание 2. Получены следующие значения критерия Стьюдента (t) и p-level, соответствующие переменным уравнения множественной линейной регрессии:
Сделать вывод о значимости коэффициентов модели. Ответ. В построенной модели присутствуют коэффициенты, которые незначимо отличаются от нуля. В целом же у переменной X8 коэффициент самый близкий к нулю, а у переменной X9 — самое высокое значение коэффициента. Коэффициенты модели линейной регрессии можно ранжировать по мере убывания незначимости с возрастанием значения t-критерия Стьюдента. Исключение резко выделяющихся наблюденийПример. Задание 3. Выявлены несколько резко выделяющихся наблюдений (выбросов, то есть наблюдений с нетипичными значениями): 10, 3, 4 (соответствуют строкам исходной таблицы данных). Эти наблюдения следует последовательно исключить из модели и по мере исключения заполнить таблицу с показателями качества модели. Исключили наблюдение 10 — заполнили значение показателей, далее исключили наблюдение 3 — заполнили и так далее. По мере исключения STATISTICA будет выдавать переменные, которые остаются значимыми в модели множественной линейной регрессии — они будут выделены красном цветом. Те, что не будут выделены красным цветом — незначимые переменные и их также нужно внести в соответствующую ячейку таблицы. По завершении исключения выбросов записать уравнение конечной множественной линейной регрессии.
Уравнение конечной множественной линейной регрессии: Случается однако, когда после исключения некоторого наблюдения исключение последующих наблюдений приводит к ухудшению показателей качества модели. Причина в том, что с исключением слишком большого числа наблюдений выборка теряет информативность. Поэтому в таких случаях следует вовремя остановиться. Исключение незначимых переменных из моделиПример. Задание 4. По мере исключения из модели множественной линейной регрессии переменных с незначимыми коэффициентами (получены при выполнении предыдущего задания, занесены в последнюю колонку таблицы) заполнить таблицу с показателями качества модели. Последняя колонка, обозначенная звёздочкой — список переменных, имеющих значимое влияние на зависимую переменную. Эти переменные STATISTICA будет выдавать выделенными красным цветом. По завершении исключения незначимых переменных записать уравнение конечной множественной линейной регрессии.
Когда осталась одна переменная, имеющая значимое влияние на зависимую переменную, больше не исключаем переменные, иначе получится, что в модели все переменные незначимы. Уравнение конечной множественной линейной регрессии после исключения незначимых переменных: Переменные X1 и X2 в задании 3 не вошли в список незначимых переменных, поэтому они вошли в уравнение конечной множественной линейной регрессии «автоматически». Нелинейные модели для сравненияПример. Задание 5. Построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных. Так как в наблюдениях переменных X9 и X10 имеется 0, а натуральный логарифм от 0 вычислить невозможно, то берутся следующие по значимости переменные: X1 и X2. Полученное уравнение нелинейной регрессии с квадратами двух наиболее значимых переменных: Показатели качества первой модели нелинейной регрессии:
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля. Полученное уравнение нелинейной регрессии с логарифмами двух наиболее значимых переменных: Показатели качества второй модели нелинейной регрессии:
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля. Применение пошаговых алгоритмов включения и исключения переменныхПример. Задание 6. Настроить пакет STATISTICA для применения пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE). Для этого в диалоговом окне MULTIPLE REGRESSION указать Advanced Options (stepwise or ridge regression). В поле Method выбрать либо Forward Stepwise (алгоритм пошагового включения), либо Backward Stepwise (алгоритм пошагового исключения). Необходимо настроить следующие параметры:
Построить, как описано выше, модели множественной линейной регрессии автоматически. В результате применения пошагового алгоритма включения получено следующее уравнение множественной линейной регрессии: Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры включения:
В результате применения пошагового алгоритма исключения получено следующее уравнение множественной линейной регрессии: Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры исключения:
Выбор самой качественной модели множественной линейной регрессииПример. Задание 7. Сравнить модели, полученные на предыдущих шагах и определить самую качественную.
Самая качественная модель множественной линейной регрессии — модель, построенная методом FORWARD STEPWISE (пошаговое включение переменных), так как коэффициент детерминации у неё самый высокий, а RSS и SEE наименьшие в сравнении значений оценок качества других регрессионных моделей. Множественная регрессия и корреляцияМНОЖЕСТВЕННАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ 2.1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ Множественная регрессия — уравнение связи с несколькими независимыми переменными где у— зависимая переменная (результативный признак); Для построения уравнения множественной регрессии чаще используются следующие функции: • линейная — • степенная – • экспонента — • гипербола — Можно использовать и другие функции, приводимые к линейному виду. Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии: Для ее решения может быть применён метод определителей:
где Другой вид уравнения множественной регрессии — уравнение регрессии в стандартизованном масштабе:
где К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (β-коэффициенты) определяются из следующей системы уравнений: Связь коэффициентов множественной регрессии Параметр a определяется как Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле:
Для расчета частных коэффициентов эластичности применяется следующая формула:
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:
Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:
Индекс множественной корреляции для уравнения в стандартизованном масштабе можно записать в виде:
При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:
парных коэффициентов корреляции;
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х1 при неизменном уровне других факторов, можно определить по формуле или по рекуррентной формуле Частные коэффициенты корреляции изменяются в пределах от -1 до 1. Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассматривается как квадрат индекса множественной корреляции:
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле где n — число наблюдений; m- число факторов. Значимость уравнения множественной регрессии в целом оценивается с помощью F — критерия Фишера: Частный F-критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора xi частный F-критерий определится как Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Съюдента сводится к вычислению значения где mbi — средняя квадратическая ошибка коэффициента регрессии bi, она может быть определена по формуле:
При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной линейной связанности. Считается, что две переменные явно коллинеарны, т. е. находятся между собой в линейной зависимости, если rxixj≥0,7. По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы rxixj (xi≠xj) были бы равны нулю. Так, для включающего три объясняющих переменные уравнения матрица коэффициентов корреляции между факторами имела бы определитель, равный 1:
так как Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0:
Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и надежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Проверка мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных Ho: Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора xj остатки имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность. При нарушении гомоскедастичности мы имеем неравенства При малом объеме выборки для оценки гетероскедастичности может использоваться метод Гольдфельда-Квандта. Основная идея теста Гольдфельда-Квандта состоит в следующем: 1) упорядочение n элементов по мере взрастания переменной x; 2) исключение из рассмотрения С центральных наблюдений; при этом (n—C):2>p, где p-число оцениваемых параметров; 3) разделение совокупности из (n—C) наблюдений на две группы (соответственно с малыми и с большими значениями фактора х) и определение по каждой из групп уравнений регрессии; При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять F-критерию со степенями свободы ((n—C-2p):2) для каждой остаточной суммы квадратов Чем больше величина R превышает табличное значения F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин. Уравнения множественной регрессии могут включать в качестве независимых переменных качественные признаки (например, профессия, пол, образование, климатические условия, отдельные регионы и т. д.). Чтобы вест такие переменные в регрессионную модель, их необходимо упорядочить и присвоить им те или иные значения, т. е. качественные переменные преобразовать в количественные. источники: http://function-x.ru/statistics_regression2.html http://pandia.ru/text/77/209/82690.php |










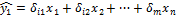









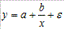 , параболы второй степени
, параболы второй степени 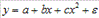 и д.р.
и д.р.

 ,
, — коэффициенты функции линейной регрессии генеральной совокупности,
— коэффициенты функции линейной регрессии генеральной совокупности, — случайная ошибка.
— случайная ошибка. ,
, — коэффициенты модели регрессии выборки,
— коэффициенты модели регрессии выборки, — ошибка.
— ошибка.
 .
.

 ,
, — матрица, транспонированная к матрице X,
— матрица, транспонированная к матрице X, — матрица, обратная к матрице
— матрица, обратная к матрице  .
. , F-статистика (статистика Фишера), сумма квадратов остатков RSS, стандартная ошибка регрессии (SEE). В случае множественной регрессии следует использовать также скорректированный коэффициент детерминации (adjusted
, F-статистика (статистика Фишера), сумма квадратов остатков RSS, стандартная ошибка регрессии (SEE). В случае множественной регрессии следует использовать также скорректированный коэффициент детерминации (adjusted 


 — независимые переменные (факторы).
— независимые переменные (факторы). ;
;



 ,
,  ,…,
,…,  ,
, — определитель системы;
— определитель системы; — частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
— частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы. ,
, ,
,  — стандартизованные переменные;
— стандартизованные переменные; — стандартизованные коэффициенты регрессии.
— стандартизованные коэффициенты регрессии.
 со стандартизованными коэффициентами
со стандартизованными коэффициентами  описывается соотношением
описывается соотношением

 .
. .
. =
= .
.

 .
. =
= .
. =
= ,
, -определитель матрицы
-определитель матрицы -определитель матрицы
-определитель матрицы

 .
.



 .
.
 ,
, и
и 
 .
. . Доказано, что величина
. Доказано, что величина  имеет приближенное распределение x2 c
имеет приближенное распределение x2 c  степенями свободы. Если фактическое значение х2 превосходит табличное (критическое)
степенями свободы. Если фактическое значение х2 превосходит табличное (критическое)  , то гипотеза Ho отклоняется. Это означает, что
, то гипотеза Ho отклоняется. Это означает, что  ,недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.
,недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.
 .
.