Показательные уравнения
О чем эта статья:
6 класс, 7 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательного уравнения
Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:
Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.
С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a
Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.
Показательные уравнения — алгоритмы и примеры вычисления
Показательные уравнения, как и любые другие, требуют поиска неизвестной переменной. Особенность в том, что она или выражение с ней находится в показателе степени.
Основные понятия и свойства
В показательных уравнениях, которые часто называют степенными, в основании находятся исключительно числа. Переменная же есть только в показателе.
Она может быть одна или являться частью выражения. Если она появляется в другом месте, приходится иметь дело с уравнениями смешанного типа.
Школьники знакомятся с простыми вычислениями уже в 7 классе, более сложные решают выпускники и студенты вузов. Если фигурирует несколько переменных и представлено больше одного уравнения, говорят об их системе.
Тогда необходимо выразить одну неизвестную через другую и искать результат методом подстановки. Поэтому умение находить значения, в которые возводят натуральные числа, пригодится на долгие годы.
Изучаются также и показательные функции: она может быть восходящей и нисходящей, в зависимости от значения переменной или выражения.
2 x = 4 – показательное уравнение с иксом в степени;
2 x = x + 12 – смешанное, ведь икс находится также и в основании.
2 – основание, оно должно соответствовать двум условиям, а именно: быть больше нуля и отличаться от единицы;
Если вместо знака «=» используются обозначения «>», « 1 = 9. Если же возвести число в степень ноль, то результат всегда будет одинаковым, а именно, равным единице: 9 0 = 1.
2. Если математическое выражение возводится в отрицательное значение, то его можно заменить дробью, где числитель – единица, а знаменатель первоначальное выражение, но уже в положительной степени. Числитель – значение, находящееся над чертой, знаменатель – под ней. Математически правило записывается в следующем виде:
3. Чтобы возвести число в степень, нужно умножить его на себя такое количество раз, которое равно ее значению, то есть р 5 = р·р·р·р·р.
4. Если нужно умножить два положительных числа, отличных от единицы и равных между собой, то нужно сложить их показатели и возвести в полученное значение основание: p 5 ·p 3 = p 5+3 = p 8 .
5. Когда требуется разделить одно число на другое, имеющие отличные показатели, нужно вычесть из одного другой и возвести в полученное значение неизменное основание: p 9 /p 3 = p 9-3 = p 6 .
6. Если необходимо возвести одну степень в другую, то нужно их перемножить. Само основание при этом остается без изменений. Его нужно возвести в полученное после арифметических действий значение: (p 3 ) 4 = p 3*4 = p 12 .
Применение свойств и правил помогает упростить выражения, быстрее произвести вычисления и получить результат.
Примеры решения показательных уравнений
Закрепить материал помогут подробные объяснения при решении показательных уравнений. Разъяснения на практике помогут изучить сложные моменты и облегчат усвоение знаний.
Задание 1
Упростить и решить уравнение: 5 3x+14 = 5 7+2x
В обеих частях примера одинаковые основания, значит, можно приравнять математические выражения, находящиеся в показателе. В результате получится:
Путем переноса чисел в одну часть, а переменных в другую, не сложно решить пример. Главное, не забывать менять знак на противоположный, плюс на минус и наоборот:
Задание 2
Выполнить вычисление и найти х:
Основания обеих частей примера – 4, оно не меняется, следовательно, можно воспользоваться изученными свойствами и получить простейшее уравнение:
Задание 3
Упростить и найти значение х:
Дроби в примере разные. Поэтому приравнять их показатели сразу не получится. Но стоит обратить внимание, что числитель одной равен знаменателю другой и наоборот.
Чтобы решить, придется вспомнить о правиле возведения в отрицательную степень, когда выражение представляется в виде дроби. Значит, числитель можно поменять местами со знаменателем.
В показателе при этом появится знак «минус»:
При равных основаниях приравниваются степени: -х = 2х + 3.
Далее придется выполнить простое задание, чтобы найти неизвестную переменную:
Задание 4
Вычислить: (3 x ) 2 = 81.
Можно представить в следующем виде: (3 x ) 2 = 3 4 .
Если воспользоваться изученными свойствами, получается: 3 2x = 3 4 .
Далее выполнить простые действия, чтобы получить результат:
Задание 5
Решить уравнение: 5 x+1 + 7·5 x-2 = 132.
Если воспользоваться свойством степеней, применяемых для умножения значений с одинаковым основанием, можно преобразовать уравнение. Общий множитель прежде всего нужно поставить за скобки, это правило регулярно применяется при решении:
5 x-2 (5 3 + 7) = 132;
Если обе части уравнения разделить или умножить на одно и то же число, результат не изменится. В данном случае необходимо разделить на число 132. Это помогает избавиться от громоздких вычислений, удлиняющих ход решения:
Далее необходимо вспомнить, что любое значение, возведенное в ноль, равно единице:
Остается только приравнять показатели и решить элементарный пример:
Задание 6
Решить показательное уравнение √4 x = 16.
Квадратный корень можно заменить степенью 1/2. Получается, что 4 имеет показатель x/2.
Значит, уравнение преобразуются в следующее:
А дальше необходимо действовать по уже проверенному и закрепленному методу:
Чтобы быстро решать показательные уравнения, нужно знать свойства степеней и умело ими пользоваться на практике. Это позволит легко находить неизвестные переменные. Полученные знания обязательно пригодятся для вычисления более сложных задач.
Существуют онлайн калькуляторы, позволяющие легко и просто решить степенные уравнения. Требуется просто вписать их в ячейку и немного подождать, пока машина справится с подсчетами. Но гораздо интереснее самому произвести арифметические действия и получить верный результат.
Интернет не всегда есть под рукой, а подобные примеры – основа решения более трудных задач, которые могут встретиться на экзамене ЕГЭ по математике. Например, логарифмических. Они могут содержать тригонометрические элементы и объемные алгебраические конструкции.
Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://nauka.club/matematika/pokazatelnye-uravneniya.html
http://www.evkova.org/pokazatelnyie-uravneniya-i-neravenstva


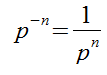

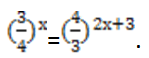
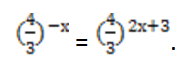
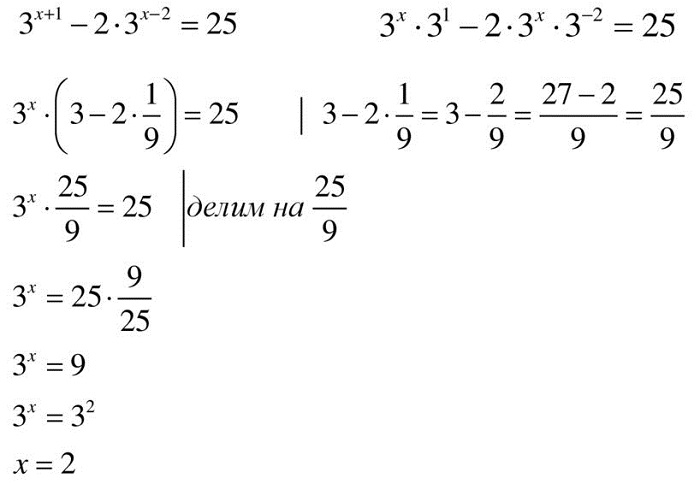










































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);










