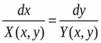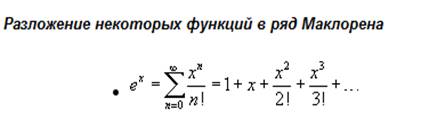Применение рядов тейлора для решения дифференциальных уравнений

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Основные понятия

Определение.Уравнение вида

связывающее аргумент х, функцию у(х) и ее производные, называется дифференциальным уравнением n-го порядка.

Определение. Общим решением дифференциального уравнения n-го порядка называется функция у = φ(х, С1,С2,…,Сn), которая зависит от аргумента х и n независимых произвольных постоянных С1, С2, …, Сn, обращающая вместе со своими производными у’, у»,…, у(n) уравнение (*) в тождество.

Определение. Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С1, С2, …, Сn определенные числовые значения.

Линейные дифференциальные уравнения первого порядка

Определение. Уравнение вида y’+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Уравнение вида y»+ρy’+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами.

Рассмотрим линейное уравнение второго порядка вида:

у которого правая часть f(x) равна нулю. Такое уравнение называется однородным.

называется характеристическим уравнением данного уравнения (1).

Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К1 и К2.

Общее решение уравнения (1) может быть записано в зависимости от величины дискриминанта D=ρ2–4q уравнения (2) следующим образом:

1. При D>0 корни характеристического уравнения вещественные и различные (К1≠К2), и общее решение имеет вид .

2. При D=0 корни характеристического уравнения вещественные и равные (К1=К2=К), и общее решение имеет вид:

От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.

Дифференциальные уравнения с разделяющимися переменными

5) Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Если оба ряда сходятся, то их сумма сходится, если оба ряда сходятся абсолютно, то их сумма сходится абсолютно. Если хотя бы один из рядов сходится абсолютно, то произведение рядов сходится.

Определение числового ряда.

Сходимость ряда.

Бесконечным числовым рядом называется выражение u1+u2+. +un+. , (1)

содержащее неограниченное число членов, где

u1 , u2 , u3 , . , un , .

— бесконечная числовая последовательность; un называется общим членом ряда.

Определение: Ряд называется сходящимся, если сумма первых его n членов стремится к конечному пределу S, называемому суммой ряда.

Геометри́ческая прогре́ссия — последовательность чисел (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии), где , : [1].

В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда.

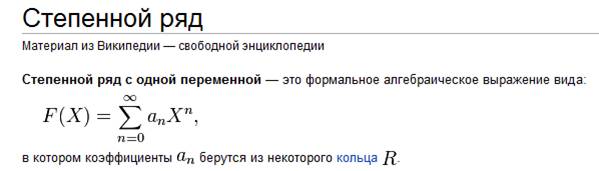
9,10) Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Особенно часто и эффективно степенные ряды используются для точного и приближенного решения дифференциальных уравнений, обыкновенных и с частными производными. Не вдаваясь в сложные теоретические обоснования, рассмотрим дифференциальное уравнение Бесселя

x2y» + xy’ + (x2 — n2)y = 0,

где n — постоянная (необязательно целая), x — независимая переменная, а y = y(x) — искомая функция. Решения этого уравнения, называемые функциями Бесселя, нашли применение практически во всех областях современного естествознания.

Будем искать y в виде обобщенного степенного ряда

где p, ak — неизвестные постоянные, причем a0 ? 0. Дифференцируя этот ряд дважды под знаком суммы, подставим выражения функции y и ее производных y’, y» в уравнение (7). Затем сделаем приведение подобных членов, и коэффициенты полученного ряда приравняем нулю. После этого получим бесконечную систему уравнений

ak[(p + k)2 — n2] + ak — 2 = 0, k = 2, 3, 4, _,

p = ? n, a1 = a3 = a5 = _ = 0,

В случае нецелого n функции y1(x) и y2(x), соответствующие значениям p = n и p = — n, являются линейно-независимыми и любое другое решение дифференциального уравнения (7) имеет вид y = c1y1(x) + + c2y2(x), где c1 , c2 — постоянные. В случае целого n эти функции отличаются друг от друга только постоянным множителем, поэтому определяют лишь одно из двух линейно-независимых решений дифференциального уравнения.

14)

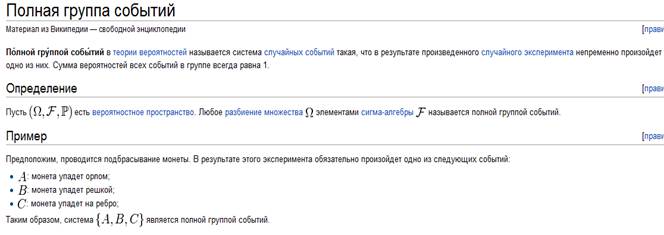
Дискретной случайной величинойназывается такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью.

Применение рядов тейлора для решения дифференциальных уравнений

Сходящиеся степенные ряды имеют разнообразные приложения. С их помощью вычисляют приближенные значения функций, пределы некоторых функций и «неберущиеся» или сложные для вычисления интегралы с заданной точностью, а также интегрируют дифференциальные уравнения.

1. Приближенное вычисление значений функций

Пусть требуется вычислить значение функции f ( x ) при x = x ₀ с заданной точностью ε>0. Предположим, что для функции в окрестности точки x ₀ имеет место теорема 3.27, то есть применима формула Тейлора (3.52) главы III с остаточным членом (3.54) в форме Лагранжа. При x ₀ = 0 получим ряд Маклорена, обозначенный ранее формулой (3.55):

Примечание. Может оказаться, что ряд Маклорена, составленный для функции f ( x ), либо расходится, либо сходится не к функции f ( x ). Говорят, что такая функция в ряд Маклорена не раскладывается

Вспомним разложения по формуле Маклорена некоторых элементарных функций, обозначенных в главе III (3.57) – (3.61), на основе которых приведём соответствующие разложения в степенной ряд:

областью сходимости рядов (9.15), (9.16), (9.17) является вся числовая прямая (–∞;+∞) ;

После выяснения сходимости на концах интервала областью сходимости ряда (9.18) является полуинтервал (–1;1].

с интервалом сходимости (–1;1) ; на концах интервала при x =± 1 сходимость ряда зависит от конкретных значений m .

Пример 9.9. Найти sin 28 0 с точностью до 0,0001.

Решение . Переведем 28 0 в действительное число. Составим пропорцию . Отсюда получим . Согласно формуле (9.15)

Полученный знакочередующийся ряд удовлетворяет условиям теоремы 9.8 Лейбница. Так как четвертый член ряда меньше заданной точности 0,0000013 sin 28 0 с точностью до 0,0001 достаточно первых трех членов ряда. Окончательно получаем .

Значение sin 28 0 , вычисленное с помощью калькулятора равно 0,46923, найденное по таблице Брадиса равно 0,4695

Примечание . В случаях знакопеременных или знакоположительных рядов составляют ряд из абсолютных величин членов и стараются подобрать положительный ряд с большими членами (часто таким рядом является сходящийся ряд геометрической прогрессии), который легко бы суммировался. В качестве оценки погрешности берут величину остатка этого нового ряда

2. Приближенное вычисление пределов функций

Применение степенных рядов к приближенному вычислению пределов различных функций является либо альтернативным методом решения, либо позволяет найти пределы, другими способами не вычисляемые. Чтобы проиллюстрировать последний случай, рассмотрим пример.

Пример 9.10. Найти предел функции .

Решение. В главе III нами были рассмотрены различные способы вычисления пределов функций с помощью замечательных пределов (пункт III.2) и теоремы 3.21 Лопиталя (пункт III.5). Однако для нахождения заданного предела данные методы решения не применимы, так как функция под пределом содержит одновременно экспоненциальную и тригонометрические функции, а в процессе дифференцирования по правилу Лопиталя числитель и знаменатель дроби усложняются.

Вычислим заданный предел путем разложения в степенные ряды все функции, содержащиеся под пределом. При этом возьмем столько членов разложений, чтобы наибольшая степень переменной равнялась четырем, так как x → 0 и x 4 дает точность вычислений не менее 0,0001.

После применения формул (9.15)-(9.17) получим:

3. Приближенное вычисление определенных интегралов

Пусть требуется вычислить с точностью до ε>0. Для приближенного вычисления неопределенных и определенных интегралов в тех случаях, когда первообразная не выражается в конечном виде через элементарные функции либо нахождение первообразной сложно или трудеёмко, также применяются сходящиеся бесконечные ряды.

Если подынтегральную функцию f ( x ) можно разложить в ряд по степеням x и интервал сходимости (– R ; R ) включает в себя отрезок [ a ; b ], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяются так же, как и при вычислении значений функций.

Пример 9.11. Вычислить , с точностью до 0,001.

Решение. Представим подынтегральную функцию в виде степенного ряда. Заменив в разложении (9.15) функции sin x аргумент x на , имеем:

Полученный ряд сходится абсолютно по теореме 9.8 (проверить самостоятельно). Так как четвертый его член по абсолютной величине 0,00011

Пример 9.12. Вычислить интеграл при с точностью до 0,0001.

Решение . Разложим по (9.17) подынтегральную функцию в ряд Маклорена, заменяя x на (– x 3 ):

На отрезке проинтегрируем данное равенство:

Получили знакочередующийся ряд, сходящийся по признаку Лейбница (теорема 9.8). Так как требуемая точность вычислений составляет 0,0001 и четвертый член ряда по модулю 0,000016 меньше 0,0001, то достаточно сложить первые три слагаемые:

4. Приближенное решение дифференциальных уравнений

В главе III.5 (схема 32) был рассмотрен механический смысл производной функции одной переменной. Если уравнение траектории движения материальной точки описывается уравнением y = f ( x ), то скорость движения − это , а ускорение − . Ряд задач, встречающихся на практике, описывают движение некой механической системы уравнениями, которые одновременно содержат все эти три характеристики − , то есть приводят к обыкновенным дифференциальным уравнениям.

Если способ решения дифференциального уравнения слишком сложен или искомое решение не выражается через элементарные функции в конечном виде, то для приближенного решения уравнения можно воспользоваться рядом (3.52) Тейлора. Рассмотрим два способа решения дифференциальных уравнений с помощью степенных рядов.

Пусть, необходимо решить уравнение второго порядка

4.1. Метод последовательного дифференцирования ДУ. Будем искать решение y=y(x) уравнения (9.20) в виде ряда Тейлора по степеням x – x ₀ :

Алгоритм решения следующий:

1) первые два коэффициента ряда берем из начальных условий (9.21);

2) третий коэффициент находим из самого уравнения (9.20), подставляя в него начальные условия ;

3) значения последующих коэффициентов , … вычисляем последовательным дифференциро-ванием заданного уравнения (9.20) по x и подстановкой в найденную производную всех полученных до этого значений при x = x ₀ ;

4) процесс дифференцирования продолжаем вплоть до определения членов ряда, количество которых обычно задается условием задачи;

5) найденные значения производных подставляем в разложение (9.22).

Ряд (9.22) представляет собой искомое частное решение уравнения (9.20) для всех значений переменной x, принадлежащих его области сходимости. Частичная сумма этого ряда будет приближенным решением заданного ДУ.

Примечание . Способ последовательного дифференцирования применим для решения дифференциальных уравнений произвольного n -го порядка. В этом случае коэффициенты первых n членов разложения берут из n заданных начальных условий; следующий ( n + 1)-ый коэффициент − из самого уравнения при подстановке в него начальных условий; с ( n + 2)-го члена ряда начинают процесс дифференцирования

Пример 9.13. Методом последовательного дифференцирования найти шесть первых членов (отличных от нуля) разложения в ряд решения уравнения .

Решение . Будем искать решение уравнения в виде степенного рада по степеням x + 1:

По условию y ( – 1)=2 , . Находим , подставив x = –1 в исходное уравнение . Для нахождения последующих коэффициентов дифференцируем заданное по условию уравнение:

Подставляя найденные значения производных в искомый ряд, получаем:

4.2. Метод неопределенных коэффициентов применяется для интегрирования линейных дифференциальных уравнений с переменными коэффициентами вида

Приближенное решение уравнения (9.23) возможно лишь в предположении, что коэффициенты и свободный член f ( x ) разлагаются в ряды по степеням x – x ₀ , сходящиеся в некотором интервале ( x ₀ – R ; x ₀ + R ). Тогда искомое решение y = y ( x ) ищется в виде степенного ряда

с неопределенными коэффициентами, количество членов которого обычно задано по условию.

Приведем краткий алгоритм решения:

1) первый коэффициент находят из уравнения при первом начальном условии y ( x ₀ )= y ₀ = c ₀

2) дифференцируют ряд (9.25)

3) второй коэффициент находят из (9.26) при втором начальном условии , после чего ряд (9.25) принимает вид

4) вычисляют вторую производную , дифференцируя ряд (9.26);

5) подставляют найденные в исходное уравнение, одновременно коэффициенты и свободный член f ( x ) заменяют их разложениями в степенные ряды;

6) раскрывают скобки, приводят подобные слагаемые и сравнивают коэффициенты при одинаковых степенях переменной x ;

7) из полученных уравнений находят неизвестные коэффициенты c_i и подставляют их найденные значения в искомый ряд (9.25).

Построенный ряд (9.25) сходится в том же интервале ( x ₀ – R ; x ₀ + R ) и является приближенным решением заданного уравнения (9.23).

Примечание . Для решения линейных ДУ с переменными коэффициентами произвольного n -го порядка их дифференцирую n раз, то есть столько раз, каков порядок заданного уравнения.

Пример 9.14. Найти первые семь членов разложения в ряд приближенного решения дифференциального уравнения , используя метод неопределенных коэффициентов.

Решение . Будем искать приближенное решение заданного уравнения в виде степенного ряда по степеням переменной x :

с учетом начальных условий

Продифференцируем дважды равенство (9.27):

Коэффициенты заданного уравнения p ₁ ( x )= – x , p ₂ ( x )=1. Разложим его правую часть в степенной ряд:

Подставим производные , функцию (9.27) и правую часть (9.28) в исходное уравнение, получим:

Приравняем коэффициенты при одинаковых степенях переменной в обеих частях последнего равенства:

Найденные значения коэффициентов подставим в разложен ие искомого решения (9.27):

. Очевидно, что приближенным решением заданного уравнения является функция y = cos x

Разложение решения уравнения в степенной ряд

Этот прием является особенно удобным в применении к линейным дифференциальным уравнениям. Проиллюстрируем его применение на примере уравнения второго порядка. Пусть дано дифференциальное уравнение второго порядка

Предположим, что коэффициенты и представляются в виде рядов, расположенных по целым положительным степеням , так что уравнение (1) можно переписать в виде

Решение этого уравнения будем искать также в виде степенного ряда

Подставляя это выражение и его производных в (2), получаем

Перемножая степенные ряды, собирая подобные члены и приравнивая нулю коэффициенты при всех степенях в левой части (4), получаем ряд уравнений:

Каждое последующее из уравнений (5) содержит одним искомым коэффициентом больше, чем предыдущее. Коэффициенты и остаются произвольными и играют роль произвольных постоянных. Первое из уравнений (5) дает , второе дает , третье — , и т.д. Вообще из (к + 1)-го уравнения можно определить , зная .

Практически удобно поступать следующим образом. Определим по описанной выше схеме два решения и , причем для выберем и , а для выберем и , что равносильно следующим начальными условиям:

Всякое решение уравнения (1) будет линейной комбинацией решений и .

Если начальные условия имеют вид , то очевидно,

Имеет место следующая теорема.

Теорема. Если ряды и сходятся при , то построенный указанным выше способом степенной ряд (3) будет также сходящимся при этих значениях и явится решением уравнения (1).

В частности, если и — многочлены от , то ряд (3) будет сходиться при любом значении .

Пример 1. Найти решения уравнения в виде степенного ряда.

Решение. Ищем в виде ряда , тогда

Подставляя и в (6), получаем

Приводя в (7) подобные члены и приравнивая нулю коэффициенты при всех степенях , получаем соотношения, из которых найдем коэффициенты

Положим для определенности, что . Тогда легко находим, что