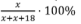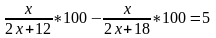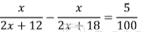Применение систем уравнений при решении прикладных задач

Методы решения систем уравнений и их применение при решении экономических задач

Уметь решать систему уравнений нужно не только и не столько в задачах, начинающихся словами «решить систему …», хотя такие задачи встречаются наиболее часто. Кроме этого, решение многих текстовых задач немыслимо без навыков работы с системами уравнений. Причем зачастую проблема состоит не в том, чтобы записать систему, адекватную текстовому условию задачи, а в том, чтобы эту систему решить!

Решить систему уравнений — это значит найти все её решения или установить, что их нет.

Существует множество методов решения системы уравнений: метод подстановки, метод алгебраического сложения, метод замены переменных, графический метод и др. Подход зависит от типа системы. Так, решение систем линейных уравнений полностью исследовано: у них найдены аналитические методы (метод Крамера) и предложено несколько численных как точных (простейший — метод Гаусса), так и приближённых (метод итераций).

Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.

При моделировании экономических задач, таких как задачи управления и планирования производства, определения оптимального размещения оборудования, оптимального плана производства, оптимального плана перевозок грузов (транспортная задача), распределения кадров и др., может быть положена гипотеза линейного представления реального мира.

Математические модели таких задач представляются линейными уравнениями. Если задача многомерна, то ее математическая модель представляется системой линейных уравнений.

Данная работа актуальна с точки зрения освоения материала и для практического применения знаний не только в математике, но и в реальных жизненных ситуациях. Например, особенно часто применять такие знания требуется в экономической сфере.

Цель работы – исследовать теоретические и практические основы эффективности использования различных методов решения систем уравнений и их применения при решении экономических задач.

Для достижения указанной цели решаются следующие задачи:

· изучить теоретические основы систем уравнений;

· рассмотреть основные методы решения систем уравнений;

· исследовать эффективность методов на конкретных примерах при решении экономических задач.

Предметом исследования являются методы решения систем уравнения.

Презентация на тему «Применение систем линейных уравнений для решения прикладных задач»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

ГПОУ «Донецкий политехнический колледж» Применение систем линейных уравнений для решения прикладных задач. Прелодаватель математики Низамова И . В. Донецк 2018

Математика – царица наук Карл Фридрих Гаусс

Системы линейных уравнений широко используются в задачах экономики, физики, электротехники, программирования и других наук.

Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных. Система линейных уравнений с n переменными:

Числа aij (i=1,2,…,m, j=1,2,…,n) называются коэффициентами при переменных, а bi (i=1,2,…,m) – свободными членами. Решение системы уравнений — это последовательность чисел (k1, k2, . kn), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x1, x2. xn дает верное числовое равенство.

Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной. Методы решения: По формулам Крамера; Исключение неизвестных ( метод Гаусса); С помощью обратной матрицы.

Метод Крамера Если главный определитель системы то система имеет единственное решение, которое можно найти по формулам Крамера: где –определитель, полученный из главного заменой i-того столбца столбцом свободных членов.

Метод Гаусса Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. Расширенная матрица содержит вместе с коэффициентами при неизвестных свободные члены системы уравнений.

Матричный метод Cистему линейных уравнений записывают в матричной форме: AX = B, где A — основная матрица системы; B — столбец свободных членов; X — столбцы решений системы; Матричное уравнение умножают слева на A–1 (матрицу, обратную к матрице A). Так как A− 1A = E, то X = A -1B. Метод применим, если определитель системы не равен 0.

Проверка домашнего задания Решить систему линейных уравнений всеми известными методами

Применение систем линейных уравнений для решения прикладных задач. Цель занятия: формировать умение составлять системы линейных уравнений по текстовому условию задачи; закрепить применение методов Крамера и Гаусса решения систем линейных уравнений.

Доклад №1. Задача по электротехнике Два источника постоянного тока соединены параллельно, имеют E1=11,5 B, r1=2,5 Oм, E1=16,5 B, r1=6 Oм, и нагрузочный резистор сопротивлением Rн=30 Oм. Определить значения и направление токов через источники и нагрузку.

В соответствии со вторым законом Кирхгофа Для контура, включающего в себя два источника и имеем: Для контура с источником и сопротивлением нагрузки при обходе по часовой стрелке имеем: Подставив числовые данные, получим:

Первое уравнение умножим на 6 и сложим со вторым и третьим. Получим: второе уравнение умножим на (-6) и сложим с третьим. Получим: Отсюда

Доклад №2. Из Москвы в Казань необходимо перевезти оборудование трех типов: I типа — 95 ед., II типа — 100 ед., III типа — 185 ед. Для перевозки оборудования завод может заказать три вида транспорта. Количество оборудования каждого типа, вмещаемого на определенный вид транспорта, приведено в таблице. Установить, сколько единиц транспорта каждого вида потребуется для перевозки этого оборудования. Тип оборудования Количество оборудования Т1 Т2 Т3 I 3 2 1 II 4 1 2 III 3 5 4

Пусть x ‒ количество единиц I-ого вида транспорта, y ‒ количество единиц II-ого вида транспорта, z ‒ количество единиц III-его вида транспорта. Тогда Решим систему уравнений методом Крамера: Δ = =12+12+20-3-30-32=-21 ; Δх = =380+740+500-185-950-800=-315; х = = 15;

Δу = =1200+570+740-300-1110-1520=-420; у = = 20; Δz = =555+600+1900-285-1500-1480=-210; Z = = 10. Ответ: Транспорта I-ого вида использовано 15 единиц, II-ого вида 20 единиц, а III-го вида 10 единиц.

Доклад №3. Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице: Найти количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. Тип заготовки Способ раскроя 1 2 3 А 3 2 1 Б 1 6 2 В 4 1 5

Обозначим через x, y, z количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. По условию задачи составим систему уравнений:

Ответ: первым способом раскраивается 90 листов, вторым – 15, третьим – 60.

Доклад №4. Частным лицом куплены три пакета акций общей стоимостью 485 ден. ед., причем акции первой группы куплены по 5 ден. ед. за акцию, второй – по 20, третьей – по 13. Через месяц стоимость акций первой, второй и третьей групп составила соответственно 6, 14 и 19 ден. ед., а стоимость всего пакета была 550 ден. ед. Еще через месяц они стоили по 8, 22 и 20 ден. ед. соответственно, а весь пакет стоил 660 ден. ед. Cколько акций каждой группы было куплено?

Пусть акции I-ой группы было куплено х штук, акций II-ой группы y штук, акций III-ей группы z штук. Согласно условию задачи имеем: Решим систему уравнений методом Крамера: Δ = = = 1400+3040+1716-1456-2090-2400=210;

= = 135800+250800+157300-120120-202730-220000=1050; = = 55000+73720+51480-57200-62700-58200=2100; = = 46200+88000+64020-54320-60500-79200=4200; x = = 5; y = = 10; z = = 20; Ответ: Акций I-й группы было куплено 5 штук, акций II-ой группы было куплено 10 штук, акций III-ей группы было куплено 20 штук.

Карл Фридрих Гаусс Карл Фридрих Гаусс родился 30 апреля 1777 г. Гаусс с детства проявлял все признаки гениальности. Главный труд всей своей жизни, «Арифметические исследования», юноша закончил ещё в 1798 г. В 1799 г. Гаусс заочно защищает диссертацию. Самым знаменитым трудом, проделанным Карлом Фридрихом Гауссом, была работа под названием «Теория движения небесных тел». Именно в ней ученый предложил теорию возмущения орбит. Знаменитая теорема алгебры, термин «гауссова кривизна», основы дифференциальной геометрии вошли в основу фундаментальных математических законов.

Габриэль Крамер Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария) в семье врача. Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики. В 18 лет он успешно защитил диссертацию. Талантливый учёный написал множество статей на самые разные темы: геометрия, история, математика, философия. В 1730 году он опубликовал труд по небесной механике. Крамер является одним из создателей линейной алгебры. В работе «Введение в анализ алгебраических кривых» Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.

Закрепление нового материала. Задача №1. Рассчитать сложную электрическую цепь, если E1=246 B, R1=0,3 Ом, E2=230 B, R2=1 Ом, R3=24 Ом, RВТ1= RВТ2=0.

Задача №2. Предприятием по производству бытовой техники в 1 квартале выпущено 4000 вентиляторов, 2000 миксеров и 6000 электрочайников на общую сумму 23 млн рублей. Во 2 квартале выпущено 3000 вентиляторов, 1000 миксеров и 4000 электрочайников на общую сумму 15,6 млн рублей. В 3 квартале выпущено 1000 вентиляторов, 3000 миксеров и 1000 электрочайников на общую сумму 7,8 млн рублей. Найти стоимость одного вентилятора, одного миксера и одного электрочайника.

Рефлексия Выберите смайлик, характеризующий ваше состояние на занятии.

Домашнее задание. Если ширину производственной прямоугольной площадки увеличить на 4 м, а ее длину уменьшить на 2 м, то ее площадь увеличится на 32 ; если же ширину уменьшить на 3 м, а длину увеличить на 1 м, то ее площадь уменьшится на 39 . Найдите длину и ширину площадки.

«Решение прикладных задач с помощью системы уравнений с двумя переменными.»

Цель урока: научиться решать задачи с процентами на сплавы и смеси с помощью составления системы уравнений, а также научиться составлять к задаче математическую модель.

Просмотр содержимого документа
««Решение прикладных задач с помощью системы уравнений с двумя переменными.»»

Учитель: Коровкина Надежда Михайловна

Тема урока: «Решение прикладных задач с помощью системы уравнений с двумя переменными.»

Тип урока: Урок закрепления изученного материала.

Цель урока: научиться решать задачи с процентами на сплавы и смеси с помощью составления системы уравнений, а также научиться составлять к задаче математическую модель.

Сегодня мы будем учиться составлять математические модели к задачам на смеси и сплавы.

Рассмотрим 2 способа составления математической модели:

описательный и с помощью таблицы.

Работа с учебником. Решаем задачи №540, 546

Рассмотрим решение и оформление задачи № 540

1 способ (описательный). Давайте разберемся.

? О чем идет речь в задаче? (ответы учащихся)

Предполагаемые ответы учащихся

Какой жизненный процесс описан в задаче?

Это задача на «смеси»

Какими основными величинами характеризуется этот процесс?

Масса и процентная концентрация

Какие ситуации описаны в задаче?

30% раствор солякой кислоты

10%раствор соляной кислоты

800г нового раствора с 15% содержанием соляной кислоты

(получен при смешивании 1 и 2 растворов)

Что известно о массах растворов?

Ничего. Принимаем за неизвестное, т.е за х и у.

Вспомните , пожалуйста, из химии или из математики , как найти массу вещества в растворе? ( m_р* %, т.е сначала мы проценты переводим в дробь и умножаем массу раствора на эту дробь)

30% = 0,3 10% = 0,1 15%=0,15

Составим математическую модель задачи

1 способ (описательный)

2 способ ( с помощью таблицы)

уравнений: х + у = 800

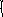
0,3 х + 0,1у = 0,15*800

Проводим анализ полученных результатов и записываем ответ.

Рассмотрим решение задачи №546 из учебника.

? Читаем задачу. О чем идет речь в задаче? …

В чем отличие от предыдущей задачи?

В отличии от предыдущей задачи здесь в сплаве содержатся 2 вещества- медь и цинк. Причем известно, что одного вещества больше, чем другого.

? Вспомните, пожалуйста, как найти процентное содержание вещества в сплаве? (Массу вещества поделить на общую массу раствора или сплава и умножить на 100%).

Составим математическую модель 1 способом (описательным) .

2 способ (в виде таблицы)

Проводим анализ полученных результатов и записываем ответ.

? Для чего нам нужно такое подробное описание задачи?

Объясняю: при подготовке к ОГЭ вы уже видели и знаете, что в №22 предлагается для решения именно задача прикладного характера, причем необходимо не просто ее решить в виде какого-то действия, а нужно привести полное подробное решение данной задачи. Только в этом случае она будет оценена в 2 балла. Вот для этого мы и учимся составлять математические модели задач.

Обучающая самостоятельная работа.

В качестве закрепления материала я предлагаю вам самим решить задачи №541, 547 (желательно разными способами)

Результат вашего решения прошу выслать мне на электронную почту в срок до 13.04.20

Если возникнут затруднения пишите! Желаю удачи!

А.Г. Мерзляк , В.Б.Полонский и др .Учебник алгебры 9 класс п. 15