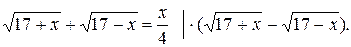Применение тождественных преобразований при решении уравнений

Тождественные преобразования и равносильность уравнений

Т.Е. Бондаренко

ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ В ПРОЦЕССЕ РЕШЕНИЯ

УРАВНЕНИЙ

Учебное пособие по элементарной математике

Воронеж

УДК 512.3(075.8)

ББК 22.141.я7

Р е ц е н з е н т ы:

кандидат педагогических наук, почётный профессор кафедры информатики и методики преподавания математики (ВГПУ) Э.С. Беляева;

кандидат педагогических наук, доцент кафедры информатики и методики преподавания математики (ВГПУ) С.А. Титоренко

Бондаренко Т. Е.

Тождественные преобразования в процессе решения уравнений: учебное пособие по элементарной математике. – Воронеж: НАУКА – ЮНИПРЕСС, 2012. – 59с.

Настоящее учебное пособие посвящено использованию тождественных преобразований в процессе решения уравнений различных видов. Предметом исследования являются преобразования, изменяющие область определения уравнения, и, как следствие, приводящие к появлению посторонних корней или к их потере. Приводится анализ каждого преобразования, и рассматриваются средства, позволяющие сохранить равносильность уравнений. В книге содержатся многочисленные примеры решения уравнений, а также задания для самостоятельной работы учащихся.

Пособие предназначено для обеспечения курса элементарной математики в педагогическом вузе. Оно может быть использовано учителями средних общеобразовательных учреждений в процессе обучения математике, для подготовки учащихся к единому государственному экзамену или для проведения элективного курса в условиях профильного обучения.

© Бондаренко Т. Е., 2012

Содержание

I. Тождественные преобразования и равносильность уравнений . . . . . . 6

II.Тождественные преобразования, изменяющие область определения

1. Приведение подобных слагаемых . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.1. Анализ преобразования. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.2. Комплекс заданий.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

2. Сокращение дробей. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

2.1. Анализ преобразования. . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11

2.2. Комплекс заданий. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14

3. Преобразования корней арифметических корней . . . . . . . . . . . . . . . 15

3.1. Анализ преобразований. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

3.2. Комплекс заданий. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

4. Преобразования логарифмов. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

4.1. Анализ преобразований. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

4.2. Комплекс заданий. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

5. Преобразование тригонометрических выражений. . . . . . . . . . . . . . . 46

5.1. Анализ преобразований . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

5.2. Комплекс заданий. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51

Приложение. Основные понятия и теоремы . . . . . . . . . . . . . . . . . . . . . . . 53

Предисловие

Изучение математики тесно связано с решением уравнений. Этот процесс иногда приводит к удивительным результатам. Казалось бы решение выполнено верно, но имеющийся в учебнике ответ не совпадает с полученным. Приведём примеры.

Решим уравнение (1) [2, № 5.110, с. 87]. Умножим обе части данного уравнения на сопряжённое выражение .

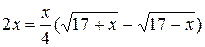
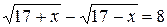
Получим уравнение (2). Очевидно, что х = 0 – корень уравнения (2). Приведём его к виду и сложим с данным уравнением (1), тогда получим уравнение , решая которое найдём корни х = -8, х = 8. Подстановкой в данное уравнение убеждаемся, что -8, 0, 8 — посторонние корни данного уравнения.

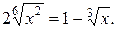
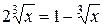
Рассмотрим ещё один пример. Решим уравнение Используя свойство арифметических корней, получим уравнение , имеющее корень Однако очевидно, что и число -1 является потерянным корнем данного уравнения.

Таким образом, иногда решение уравнения может привести к появлению посторонних корней или к их потере. Возникает вопрос, почему это происходит? В настоящем пособии приводится подробный ответ на этот вопрос для случая, когда выполняются тождественные преобразования выражений, входящих в данное уравнение. В нём перечислены преобразования, выполнение которых может привести к изменениям множества корней уравнения, и описаны средства, позволяющие сохранить его. Пособие содержит многочисленные примеры с решениями и упражнения для самостоятельной работы учащихся.

Уравнения, в которых могут появиться посторонние решения или происходит их потеря представлены в различных литературных источниках. Некоторые из них приведены в списке литературы. Особенно интересные задания включены из книг [1], [2], [3]. Однако отличительной особенностью данного пособия является его тематическая направленность и систематизация учебного материала.

Автор выражает благодарность рецензентам Э.С.Беляевой, С.А Титоренко за участие в совершенствовании пособия и надеется, что оно послужит повышению качества математической подготовки студентов и школьников.

Тождественные преобразования и равносильность уравнений

Решение данного уравнения – это процесс, состоящий в переходе к другим уравнениям до тех пор, пока не будет получено уравнение с очевидными корнями. Такие переходы осуществляются посредством различных преобразований. При этом одни преобразования приводят к уравнению с такими же корнями (равносильному данному), другие — не обладают таким свойством. Напомним, что два уравнения f₁(x)=g₁(x) и f₂(x)=g₂(x) называются равносильными (эквивалентными) на множестве М, если они имеют одни и те же решения, принадлежащие этому множеству. Преобразования, сохраняющие решения, изучаются в теории равносильных уравнений. Основное содержаниеэтой теории составляют теоремы, гарантирующие замену данного уравнения ему равносильным. Наряду с основными понятиями они приведены в приложении к настоящему курсу (с.49). Особый интерес представляет для нас теорема 1. Приведём её формулировку: если в уравнении f₁(x)=g₁(x) выполнить тождественное преобразование выражений f₁(x) или (и) g₁(x), по формуле, не меняющей область определения данного уравнения D, то получится уравнение f₂(x)=g₂(x), равносильное данному уравнению на множестве D.

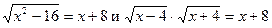
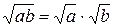
Например, в соответствии с теоремой 1 уравнения х 3 +3х 2 — 4х-12=0и(х+3)(х-2)(х+2)=0 равносильны на множестве всех действительных чисел, а уравнения не равносильны, так как х=-5, являясь корнем первого уравнения, не является корнем второго уравнения. Причина нарушения равносильности состоит в том, что в результате выполненного преобразования по формуле изменилась (сузилась) область определения данного уравнения, что привело к потере корня.

Докажем теорему 1 учитывая, что каждое уравнение вида f(x)=g(x) может быть приведено к виду F(x)=0.

Дано: уравнение F₁(x) = 0 (1) с областью определения D,

р – формула (тождество), посредством которого выполняется преобразование выражения F₁(x), не изменяющая D,

F₂(x) = 0 (2) – уравнение, полученное из данного уравнения в результате преобразования.

Доказать: уравнения (1) и (2) равносильны.

Пусть х₁ – корень уравнения (1), тогда x₁ÎD и F₁(x₁) = 0 – истинное числовое равенство. В результате применения тождества р выражение F₁(x) примет вид F₂(x). Область определения D не изменилась, то есть F₂(x₁) имеет смысл. По определению тождественно равных выражений F₂(x₁) = F₁(x₁), то есть F₂(x₁) = 0 – истинное числовое равенство, следовательно, x₁ – корень уравнения (2).

Обратно. Пусть х₂ – корень уравнения (2), тогда x₂ÎD и F₂(x₂) = 0 – истинное числовое равенство. В результате применения тождества р выражение F₂(x) примет вид F₁(x). Область определения D не изменилась, то есть F₁(x₂) имеет смысл. По определению тождественно равных выражений F₁(x₂) = 0 – истинное числовое равенство, что означает x₂ – корень уравнения (1). Равносильность доказана.

Таким образом, с преобразованиями, не изменяющими области определения данного уравнения, ситуация ясна. Однако открытым остаётся вопрос, как действовать, если тождественное преобразование меняет область определения данного уравнения. При этом оно может расширить её, и тогда возможны посторонние корни, либо сузить, что может привести к потере корней.

Выявим и исследуем тождественные преобразования, обладающие свойством расширять или сужать область определения уравнения, и определим для них средства сохранения равносильности уравнений.

Тождественные преобразования выражений, их виды

Тождественные преобразования представляют собой работу, которую мы проводим с числовыми и буквенными выражениями, а также с выражениями, которые содержат переменные. Все эти преобразования мы проводим для того, чтобы привести исходное выражение к такому виду, который будет удобен для решения задачи. Основные виды тождественных преобразований мы рассмотрим в этой теме.

Тождественное преобразование выражения. Что это такое?

Впервые встречаемся с понятием тождественных преобразованный мы на уроках алгебры в 7 классе. Тогда же мы впервые знакомимся с понятием тождественно равных выражений. Давайте разберемся с понятиями и определениями, чтобы облегчить усвоение темы.

Тождественное преобразование выражения – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.

Часто это определение используется в сокращенном виде, в котором опускается слово «тождественное». Предполагается, что мы в любом случае проводим преобразование выражения таким образом, чтобы получить выражение, тождественное исходному, и это не требуется отдельно подчеркивать.

Проиллюстрируем данное определение примерами.

Если мы заменим выражение x + 3 − 2 на тождественно равное ему выражение x + 1 , то мы проведем при этом тождественное преобразование выражения x + 3 − 2 .

Замена выражения 2 · a 6 на выражение a 3 – это тождественное преобразование, тогда как замена выражения x на выражение x 2 не является тождественным преобразованием, так как выражения x и x 2 не являются тождественно равными.

Обращаем ваше внимание на форму записи выражений при проведении тождественных преобразований. Обычно мы записываем исходное и полученное в ходе преобразования выражения в виде равенства. Так, запись x + 1 + 2 = x + 3 означает, что выражение x + 1 + 2 было приведено к виду x + 3 .

Последовательное выполнение действий приводит нас к цепочке равенств, которая представляет собой несколько расположенных подряд тождественных преобразований. Так, запись x + 1 + 2 = x + 3 = 3 + x мы понимаем как последовательное проведение двух преобразований: сначала выражение x + 1 + 2 привели к виду x + 3 , а его – к виду 3 + x .

Тождественные преобразования и ОДЗ

Ряд выражений, которые мы начинаем изучать в 8 классе, имеют смысл не при любых значениях переменных. Проведение тождественных преобразований в этих случаях требует от нас внимания к области допустимых значений переменных (ОДЗ). Выполнение тождественных преобразований может оставлять ОДЗ неизменной или же сужать ее.

При выполнении перехода от выражения a + ( − b ) к выражению a − b область допустимых значений переменных a и b остается прежней.

Переход от выражения x к выражению x 2 x приводит к сужению области допустимых значений переменной x от множества всех действительных чисел до множества всех действительных чисел, из которого был исключен ноль.

Тождественное преобразование выражения x 2 x выражением х приводит к расширению области допустимых значений переменной x от множества всех действительных чисел за исключением нуля до множества всех действительных чисел.

Сужение или расширение области допустимых значений переменных при проведении тождественных преобразований имеет значение при решении задач, так как может повлиять на точность проведения вычислений и привести к появлению ошибок.

Основные тождественные преобразования

Давайте теперь посмотрим, какими бывают тождественные преобразования и как они выполняются. Выделим те виды тождественных преобразований, с которыми нам приходится иметь дело чаще всего, в группу основных.

Помимо основных тождественных преобразований существует ряд преобразований, которые относятся к выражениям конкретного вида. Для дробей это приемы сокращения и приведения к новому знаменателю. Для выражений с корнями и степенями все действия, которые выполняются на базе свойств корней и степеней. Для логарифмических выражений действия, которые проводятся на основе свойств логарифмов. Для тригонометрических выражений все действия с использованием тригонометрических формул. Все эти частные преобразования подробно разбираются в отдельных темах, которые можно найти на нашем ресурсе. В связи с этим в этой стстье мы на них останавливаться не будем.

Перейдем к рассмотрению основных тождественных преобразований.

Перестановка местами слагаемых, множителей

Начнем с перестановки слагаемых местами. С этим тождественным преобразованием мы имеем дело чаще всего. И основным правилом здесь можно считать следующее утверждение: в любой сумме перестановка слагаемых местами не отражается на результате.

Основано это правило на переместительном и сочетательном свойствах сложения. Эти свойства позволяют нам переставлять слагаемые местами и получать при этом выражения, которые тождественно равны исходным. Именно поэтому перестановка слагаемых местами в сумме является тождественным преобразованием.

У нас есть сумма трех слагаемых 3 + 5 + 7 . Если мы поменяем местами слагаемые 3 и 5 , то выражение примет вид 5 + 3 + 7 . Вариантов перестановки местами слагаемых в данном случае несколько. Все они приводят к получению выражений, тождественно равных исходному.

В качестве слагаемых в сумме могут выступать не только числа, но и выражения. Их точно так же, как и числа, можно переставлять местами, не влияя на конечный результат вычислений.

В сумме трех слагаемых 1 a + b , a 2 + 2 · a + 5 + a 7 · a 3 и — 12 · a вида 1 a + b + a 2 + 2 · a + 5 + a 7 · a 3 + ( — 12 ) · a слагаемые можно переставить, например, так ( — 12 ) · a + 1 a + b + a 2 + 2 · a + 5 + a 7 · a 3 . В свою очередь можно переставить местами слагаемые в знаменателе дроби 1 a + b , при этом дробь примет вид 1 b + a . А выражение под знаком корня a 2 + 2 · a + 5 тоже является суммой, в которой можно поменять местами слагаемые.

Точно так же, как и слагаемые, в исходных выражениях можно менять местами множители и получать тождественно верные уравнения. Проведение этого действия регулируется следующим правилом:

В произведении перестановка множителей местами не влияет на результат вычислений.

Основано это правило на переместительном и сочетательном свойствах умножения, которые подтверждают верность тождественного преобразования.

Произведение 3 · 5 · 7 перестановкой множителей можно представить в одном из следующих видов: 5 · 3 · 7 , 5 · 7 · 3 , 7 · 3 · 5 , 7 · 5 · 3 или 3 · 7 · 5 .

Перестановка множителей в произведении x + 1 · x 2 — x + 1 x даст x 2 — x + 1 x · x + 1

Раскрытие скобок

Скобки могут содержать записи числовых выражений и выражений с переменными. Эти выражения могут быть преобразованы в тождественно равные выражения, в которых скобок не будет вообще или их будет меньше, чем в исходных выражениях. Этот способ преобразования выражений называют раскрытием скобок.

Проведем действия со скобками в выражении вида 3 + x − 1 x для того, чтобы получить тождественно верное выражение 3 + x − 1 x .

Выражение 3 · x — 1 + — 1 + x 1 — x можно преобразовать в тождественно равное выражение без скобок 3 · x — 3 — 1 + x 1 — x .

Правила преобразования выражений со скобками мы подробно разобрали в теме «Раскрытие скобок», которая размещена на нашем ресурсе.

Группировка слагаемых, множителей

В случаях, когда мы имеем дело с тремя и большим количеством слагаемых, мы можем прибегнуть к такому виду тождественных преобразований как группировка слагаемых. Под этим способом преобразований подразумевают объединение нескольких слагаемых в группу путем их перестановки и заключения в скобки.

При проведении группировки слагаемые меняются местами таким образом, чтобы группируемые слагаемые оказались в записи выражения рядом. После этого их можно заключить в скобки.

Возьмем выражение 5 + 7 + 1 . Если мы сгруппируем первое слагаемое с третьим, то получим ( 5 + 1 ) + 7 .

Группировка множителей проводится аналогично группировке слагаемых.

В произведении 2 · 3 · 4 · 5 можно сгруппировать первый множитель с третьим, а второй – с четвертым, при этом придем к выражению ( 2 · 4 ) · ( 3 · 5 ) . А если бы мы сгруппировали первый, второй и четвертый множители, то получили бы выражение ( 2 · 3 · 5 ) · 4 .

Слагаемые и множители, которые группируются, могут быть представлены как простыми числами, так и выражениями. Правила группировки были подробно разобраны в теме «Группировка слагаемых и множителей».

Замена разностей суммами, частных произведениями и обратно

Замена разностей суммами стала возможна благодаря нашему знакомству с противоположными числами. Теперь вычитание из числа a числа b можно рассматривать как прибавление к числу a числа − b . Равенство a − b = a + ( − b ) можно считать справедливым и на его основе проводить замену разностей суммами.

Возьмем выражение 4 + 3 − 2 , в котором разность чисел 3 − 2 мы можем записать как сумму 3 + ( − 2 ) . Получим 4 + 3 + ( − 2 ) .

Все разности в выражении 5 + 2 · x − x 2 − 3 · x 3 − 0 , 2 можно заменить суммами как 5 + 2 · x + ( − x 2 ) + ( − 3 · x 3 ) + ( − 0 , 2 ) .

Мы можем переходить к суммам от любых разностей. Аналогично мы можем произвести обратную замену.

Замена деления на умножение на число, обратное делителю, становится возможным благодаря понятию взаимно обратных чисел. Это преобразование можно записать равенством a : b = a · ( b − 1 ) .

Это правило было положено в основу правила деления обыкновенных дробей.

Частное 1 2 : 3 5 можно заменить произведением вида 1 2 · 5 3 .

Точно также по аналогии деление может быть заменено умножением.

В случае с выражением 1 + 5 : x : ( x + 3 ) заменить деление на x можно на умножение на 1 x . Деление на x + 3 мы можем заменить умножением на 1 x + 3 . Преобразование позволяет нам получить выражение, тождественное исходному: 1 + 5 · 1 x · 1 x + 3 .

Замена умножения делением поводится по схеме a · b = a : ( b − 1 ) .

В выражении 5 · x x 2 + 1 — 3 умножение можно заменить делением как 5 : x 2 + 1 x — 3 .

Выполнение действий с числами

Выполнение действий с числами подчиняется правилу порядка выполнения действий. Сначала проводятся действия со степенями чисел и корнями из чисел. После этого мы заменяем логарифмы, тригонометрические и прочие функции на их значения. Затем выполняются действия в скобках. И затем уже можно проводить все остальные действия слева направо. Важно помнить, что умножение и деление проводят до сложения и вычитания.

Действия с числами позволяют преобразовать исходное выражение в тождественное равное ему.

Преобразуем выражение 3 · 2 3 — 1 · a + 4 · x 2 + 5 · x ,выполнив все возможные действия с числами.

Решение

Первым делом обратим внимание на степень 2 3 и корень 4 и вычислим их значения: 2 3 = 8 и 4 = 2 2 = 2 .

Подставим полученные значения в исходное выражение и получим: 3 · ( 8 — 1 ) · a + 2 · ( x 2 + 5 · x ) .

Теперь проведем действия в скобках: 8 − 1 = 7 . И перейдем к выражению 3 · 7 · a + 2 · ( x 2 + 5 · x ) .

Нам осталось выполнить умножение чисел 3 и 7 . Получаем: 21 · a + 2 · ( x 2 + 5 · x ) .

Ответ: 3 · 2 3 — 1 · a + 4 · x 2 + 5 · x = 21 · a + 2 · ( x 2 + 5 · x )

Действиям с числами могут предшествовать другие виды тождественных преобразований, таких, например, как группировка чисел или раскрытие скобок.

Возьмем выражение 3 + 2 · ( 6 : 3 ) · x · ( y 3 · 4 ) − 2 + 11 .

Решение

Первым делом проведем замену частного в скобках 6 : 3 на его значение 2 . Получим: 3 + 2 · 2 · x · ( y 3 · 4 ) − 2 + 11 .

Раскроем скобки: 3 + 2 · 2 · x · ( y 3 · 4 ) − 2 + 11 = 3 + 2 · 2 · x · y 3 · 4 − 2 + 11 .

Сгруппируем числовые множители в произведении, а также слагаемые, являющиеся числами: ( 3 − 2 + 11 ) + ( 2 · 2 · 4 ) · x · y 3 .

Выполним действия в скобках: ( 3 − 2 + 11 ) + ( 2 · 2 · 4 ) · x · y 3 = 12 + 16 · x · y 3

Ответ: 3 + 2 · ( 6 : 3 ) · x · ( y 3 · 4 ) − 2 + 11 = 12 + 16 · x · y 3

Если мы работаем с числовыми выражениями, то целью нашей работы будет нахождение значения выражения. Если же мы преобразуем выражения с переменными, то целью наших действий будет упрощение выражения.

Вынесение за скобки общего множителя

В тех случаях, когда слагаемые в выражении имеют одинаковый множитель, то мы можем вынести этот общий множитель за скобки. Для этого нам сначала необходимо представить исходное выражение как произведение общего множителя и выражения в скобках, которое состоит из исходных слагаемых без общего множителя.

В числовом выражении 2 · 7 + 2 · 3 мы можем вынести общий множитель 2 за скобки и получить тождественно верное выражение вида 2 · ( 7 + 3 ) .

Освежить в памяти правил вынесения общего множителя за скобки вы можете в соответствующем разделе нашего ресурса. В материале подробно рассмотрены правила вынесения общего множителя за скобки и приведены многочисленные примеры.

Приведение подобных слагаемых

Теперь перейдем к суммам, которые содержат подобные слагаемые. Тут возможно два варианта: суммы, содержащие одинаковые слагаемые, и суммы, слагаемые которых отличаются числовым коэффициентом. Действия с суммами, содержащими подобные слагаемые, носит название приведения подобных слагаемых. Проводится оно следующим образом: мы выносим общую буквенную часть за скобки и проводим вычисление суммы числовых коэффициентов в скобках.

Рассмотрим выражение 1 + 4 · x − 2 · x . Мы можем вынести буквенную часть x за скобки и получить выражение 1 + x · ( 4 − 2 ) . Проведем вычисление значения выражения в скобках и получим сумму вида 1 + x · 2 .

Замена чисел и выражений тождественно равными им выражениями

Числа и выражения, из которых составлено исходное выражение, можно заменять тождественно равными им выражениями. Такое преобразование исходного выражения приводит к тождественно равному ему выражению.

Рассмотрим выражение 3 + x . Здесь число 3 может быть заменено суммой 1 + 2 . Так мы получим выражение ( 1 + 2 ) + x , тождественно равное исходному.

Рассмотрим выражение 1 + a 5 , в котором степень a 5 мы можем заменить тождественно равным ей произведением, например, вида a · a 4 . Это нам даст выражение 1 + a · a 4 .

Выполненное преобразование искусственное. Оно имеет смысл лишь при подготовке к проведению других преобразований.

Рассмотрим преобразование суммы 4 · x 3 + 2 · x 2 . Здесь слагаемое 4 · x 3 мы можем представить как произведение 2 · x 2 · 2 · x . В результате исходное выражение принимает вид 2 · x 2 · 2 · x + 2 · x 2 . Теперь мы можем выделить общий множитель 2 · x 2 и вынести его за скобки: 2 · x 2 · ( 2 · x + 1 ) .

Прибавление и вычитание одного и того же числа

Прибавление и одновременное вычитание одного и того же числа или выражения являетс искусственным приемом преобразования выражений.

Рассмотрим выражение x 2 + 2 · x . Мы можем прибавить или отнять от него единицу, что позволит нам в последующем провести еще одно тождественное преобразование — выделить квадрат двучлена: x 2 + 2 · x = x 2 + 2 · x + 1 − 1 = ( x + 1 ) 2 − 1 .

Решение уравнений через преобразования

В этой статье мы подробно и всесторонне разберем, как осуществляется решение уравнений через проведение преобразований. Сначала расскажем, в чем суть метода. Дальше перечислим преобразования уравнений, которые используются при решении. Обязательно обговорим, на что стоит обращать особое внимание при проведении преобразований. В заключение рассмотрим решения примеров.

Суть метода

Суть метода решения уравнений через преобразования состоит в использовании преобразований уравнения для построения цепочки равносильных уравнений и уравнений-следствий с целью получения достаточно простого в плане решения конечного уравнения, по решению которого можно найти решения исходного уравнения.

Алгоритм

Схематично процесс решения уравнения через преобразования можно представить следующим образом. Исходное уравнение, обозначим его (1), преобразуется в равносильное уравнение или уравнение-следствие (2). Оно преобразуется в равносильное уравнение или уравнение-следствие (3). И так далее до уравнения (n), которое мы в состоянии решить.

Понятно, что если все преобразования равносильные, то уравнение (n) равносильно исходному уравнению (1), и решение уравнения (n) является интересующим нас решением исходного уравнения (1). Если же хотя бы для одного из переходов используется преобразование, которое в общем случае не является равносильным, то уравнение (n) является уравнением-следствием для исходного. Это означает, что среди корней уравнения (n) могут быть корни, посторонние для исходного уравнения (1). Избавиться от них позволяет отсеивание посторонних корней.

Приведенная информация позволяет записать алгоритм решения уравнений через преобразования:

• Выстроить цепочку равносильных уравнений и уравнений-следствий до уравнения, которое мы в состоянии решить.
• Решить полученное уравнение.
  • Если все преобразования были равносильными, то полученное решение является искомым.
  • Если среди проведенных преобразований были такие, которые в общем случае не являются равносильными, то провести отсеивание посторонних корней.

Какие преобразования используются? Список

Все основные преобразования, которые используются при решении уравнений, подробно описаны в этой статье. Здесь мы просто перечислим их в виде списка:

• Замена выражений, находящихся в левой и правой частях уравнения, тождественно равными им выражениями.
  • Перестановка местами слагаемых и множителей.
  • Раскрытие скобок.
  • Группировка слагаемых и/или множителей.
  • Вынесение за скобки общего множителя.
  • Замена числовых выражений их значениями.
  • Выполнение действий с одночленами и многочленами.
  • Приведение подобных слагаемых.
  • Сокращение дробей.
  • Замена нулем произведений с нулевыми множителями и дробей с нулем в числителе.
  • Использование тождеств, отражающих определения и свойства корней, степеней, логарифмов, тригонометрических функций и т.п.
• Прибавление к обеим частям уравнения одного и того же числа или вычитание из обеих частей уравнения одного и того же числа.
• Прибавление к обеим частям уравнения одного и того же выражения или вычитание из обеих частей уравнения одного и того же выражения.
• Перенос слагаемого из одной части уравнения в другую со знаком, измененным на противоположный.
• Умножение или деление обеих частей уравнения на одно и то же число, отличное от нуля.
• Умножение или деление обеих частей уравнения на одно и то же выражение.
• Возведение обеих частей уравнения в одну и ту же натуральную степень.
• Освобождение от внешней функции.
• Извлечение корня одной и той же степени из обеих частей уравнения.
• Логарифмирование.
• Потенцирование.

На что обращать особое внимание при проведении преобразований?

На ОДЗ

При проведении преобразований необходимо держать под контролем ОДЗ. Зачем? Сейчас мы с этим разберемся.

ОДЗ при переходе от одного уравнения к другому может оставаться неизменной, расширяться или сужаться. Приведем примеры. В результате перехода от уравнения 4·x=x+3 к уравнению 4·x−x=3 ОДЗ не изменяется. Переход от уравнения 1/x−1/x+x 2 =0 к уравнению x 2 =0 сопровождается расширением ОДЗ с множества (−∞, 0)∪(0, +∞) до множества всех действительных чисел R . А преобразование уравнения lgx 2 =2 к виду 2·lgx=2 сопровождается сужением ОДЗ: для исходного уравнения ОДЗ есть множество (−∞, 0)∪(0, +∞) , а для полученного — (0, +∞) . Ну и что с того? А вот что: за счет расширения ОДЗ могут появиться корни, посторонние для исходного уравнения, а сужение ОДЗ может быть причиной потери корней. Для иллюстрации сказанного вновь обратимся к приведенным примерам. При переходе от уравнения 1/x−1/x+x 2 =0 к уравнению x 2 =0 появляется корень x=0 , посторонний для исходного уравнения. А в результате замены уравнения lgx 2 =2 уравнением 2·lgx=2 происходит потеря корня x=−10 .

В расширении ОДЗ при преобразовании уравнений нет ничего особо страшного – просто после решения последнего уравнения цепочки равносильных уравнений и уравнений-следствий необходимо позаботиться об отсеивании корней, посторонних для исходного уравнения.

А вот от преобразований, в результате проведения которых сужается ОДЗ, необходимо отказаться. Точнее, от них стоит отказываться лишь тогда, когда ОДЗ сужается на множество, содержащее бесконечное количество элементов. Преобразования, в результате проведения которых из ОДЗ выпадает некоторое конечное количество чисел, допустимы. Для их проведения достаточно отдельно проверить выпадающие из ОДЗ числа на предмет того, какие из них являются корнями решаемого уравнения. Типичным таким преобразованием является деление обеих частей уравнения на выражение, обращающееся в нуль на ОДЗ. Подробнее об этом мы поговорим в статье «Как избежать потери корней при решении уравнений».

Итак, контролировать ОДЗ нужно, чтобы при проведении преобразований не терять корни, и понимать, когда необходимо проводить отсеивание посторонних корней, а когда это действие необязательно.

На тождественность

При проведении преобразований, заключающихся в замене выражений тождественно равными выражениями, нужно очень внимательно следить за тем, чтобы выражения были именно тождественно равными. Зачем? Это гарантирует, что уравнение, полученное в результате проведения преобразования, равносильно исходному уравнению или является его следствием. Замена выражения не тождественно равным ему выражением не гарантирует получение равносильного уравнения или уравнения-следствия, а это означает, что по корням полученного уравнения невозможно будет сделать вывод о корнях исходного уравнения.

Для примера возьмем уравнение . Его можно решить, например, методом возведения обеих частей в квадрат. Указанный метод позволяет найти единственный корень этого уравнения: . А теперь давайте допустим, что нам захотелось решить это уравнение через преобразования, и мы сделали это так:

Что мы сделали не так? Мы ошиблись в самом первом преобразовании – в замене выражения x+3 выражением . А дело здесь в том, что выражения x+3 и не являются тождественно равными. Действительно, их значения различны при x+3 . В результате мы получили неправильное решение.

На необходимость отсеивания посторонних корней при возведении обеих частей уравнения в четную степень

Решение уравнений, особенно иррациональных, может проводиться через преобразование, заключающееся в возведении обеих частей уравнения в одну и ту же натуральную степень. Это преобразование детально разобрано в статье «Решение иррациональных уравнений методом возведения обеих частей в одну и ту же степень». Там обосновано, что возведение обеих частей уравнения в одну и ту же нечетную степень является равносильным преобразованием, а возведение в одну и ту же четную степень в общем случае приводит к уравнению-следствию. Из этого следует, что при решении уравнения путем возведения его обеих частей в одну и ту же четную степень нужно обязательно позаботиться об отсеивании посторонних корней.

Обратимся к уравнению для наглядности. Его решение можно получить, если прибегнуть к возведению обеих частей уравнения в квадрат. Это преобразование позволяет перейти к уравнению . Одним из корней полученного уравнения является число −3/2 , в чем легко убедиться, выполнив проверку подстановкой. Но −3/2 – это посторонний корень для исходного уравнения , так как его подстановка дает неверное равенство 5/2=−5/2 . Этот посторонний корень появляется из-за проведенного нами преобразования – из-за возведения обеих частей уравнения в одну и ту же четную степень, в нашем случае в квадрат. Действительно, возведение в квадрат из неверного равенства 5/2=−5/2 делает верное (5/2) 2 =(−5/2) 2 .

Итак, при использовании преобразования, которое заключается в возведении обеих частей уравнения в одну и ту же четную степень, нельзя упускать из внимания необходимость отсеивания посторонних корней.

На условия, при которых возможно проведение отдельных преобразований

Некоторые преобразования уравнений можно проводить лишь при выполнении определенных условий. В пример приведем преобразование, заключающееся в освобождении от внешней функции. Для его проведения нужно, чтобы функция принимала каждое свое значение только по одному разу (в частности, была возрастающей или убывающей). Если это условие не выполняется, то указанное преобразование уравнения может привести к потере корней. Продемонстрируем это, обратившись к уравнению (x+3) 12 =(2·x−6) 12 . Освобождение от внешней функции возведения в двенадцатую степень приводит к уравнению x+3=2·x−6 , единственным корнем которого является x=9 . При таком переходе происходит потеря корня x=1 . Причина этого кроется в игнорировании условия, при котором возможно освобождение от внешней функции.

Помимо отбрасывания внешней функции, выполнения определенных условий требуют следующие преобразования:

• извлечение корня из обеих частей уравнения,
• логарифмирование,
• потенцирование.

Так что прежде чем провести задуманное преобразование уравнения, надо обратить пристальное внимание условия, при которых это преобразование можно осуществить. И только если они выполнены или преобразование не требует выполнения никаких особых условий, то можно смело его проводить.

Примеры решения уравнений

Метод решения уравнений через преобразования для некоторых видов уравнений является основным. Например, через преобразования решаются любые линейные уравнения с отличным от нуля коэффициентом при x . Так решение уравнения 2·x−1=0 можно представить в виде следующей цепочки уравнений, получающейся в результате проведения преобразований:
2·x−1=0 ,
2·x=1 (перенос слагаемого из одной части уравнения в другую с противоположным знаком),
(2·x):2=1:2 (деление обеих частей уравнения на отличное от нуля число 2 ),
2·x:2=1:2 (замена выражения в левой части уравнения тождественно равным ему выражением, полученным в результате раскрытия скобок),
2:2·x=1:2 (замена выражения в левой части уравнения тождественно равным ему выражением, полученным в результате перестановки местами множителей),
1·x=1/2 (замена выражения в левой части уравнения тождественно равным ему выражением, полученным в результате замены числовых выражений их значениями),
x=1/2 (замена выражения в левой части уравнения тождественно равным ему выражением).

Понятно, что так подробно преобразования уравнений никто не расписывает. Многие преобразования проводятся в уме. Но рекомендуем не увлекаться с устными преобразованиями. Целесообразно проводить в уме только самые простые преобразования, остальные лучше делать на бумаге. Так лучше прослеживается логика решения, а вероятность сделать ошибку при проведении преобразований снижается.

Часто метод решения уравнений через преобразования используется совместно с другими методами решения уравнений. Например, решение уравнения может начинаться с преобразований, дальше может вводиться новая переменная, уравнение с новой переменной может решаться через преобразования, а полученные после возврата к старой переменной уравнения могут решаться функционально-графическим методом.

Другие примеры решения уравнений через преобразования Вы без труда найдете, побродив по статьям раздела «Решение уравнений».