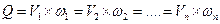Применение уравнения бернулли при расчете коротких трубопроводов

Применение уравнения бернулли при расчете коротких трубопроводов

При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности (расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода на заданных расходе и потерях напора.

В практике трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных передач.

Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы.

Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые исложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.

Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней жидкости, давлением газа.

Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве (рис. 6.1), имеет общую длину l и диаметр d, а также содержит ряд местных сопротивлений (вентиль, фильтр и обратный клапан). В начальном сечении трубопровода 1-1 геометрическая высота равна z₁ и избыточное давление Р₁, а в конечном сечении 2-2 — соответственно z₂ и Р₂. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна ν.

Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях одинакова и α₁ = α₂, то скоростной напор можно не учитывать. При этом получим

Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором Н_потр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором Н_расп. Такой напор складывается из геометрической высоты H_потр, на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.

Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую эквивалентную геометрическую высоту

а последнее слагаемое Σh — как степенную функцию расхода

где K — величина, называемая сопротивлением трубопровода;
Q — расход жидкости;
m — показатель степени, который имеет разные значения в зависимости от режима течения.

Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно

Численные значения эквивалентных длин l_экв для различных местных сопротивлений обычно находят опытным путем.

Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем

По этим формулам можно построить кривую потребного напора в зависимости от расхода. Чем больше расход Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор Н_потр. При ламинарном течении эта кривая изображается прямой линией (рис.6.2, а), при турбулентном — параболой с показателем степени равном двум (рис.6.2, б).

Крутизна кривых потребного напора зависит от сопротивления трубопровода K и возрастает с увеличением длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.

Величина статического напора Н_ст положительна в том случае, когда жидкость движется вверх или в полость с повышенным давлением, и отрицательна при опускании жидкости или движении в полость с пониженным давлением. Точка пересечения кривой потребного напора с осью абсцисс (точка А) определяет расход при движении жидкости самотеком. Потребный напор в этом случае равен нулю.

Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода.Характеристикой трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:

Простые трубопроводы могут соединяться между собой, при этом их соединение может бытьпоследовательным или параллельным.

Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно (рис. 6.3, а).

При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками М и Nравна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:

Эти уравнения определяют правила построения характеристик последовательного соединения труб (рис. 6.3, б). Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.

Параллельное соединение. Такое соединение показано на рис. 6.4, а. Трубопроводы 1, 2 и 3 расположены горизонтально.

Обозначим полные напоры в точках М и N соответственно H_M и H_N , расход в основной магистрали (т.е. до разветвления и после слияния) — через Q, а в параллельных трубопроводах через Q₁, Q₂ и Q₃; суммарные потери в этих трубопроводах через Σ₁ , Σ₂ и Σ₃.

Очевидно, что расход жидкости в основной магистрали

Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N :

Отсюда делаем вывод, что

т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом

где K и m — определяются в зависимости от режима течения.

Из двух последних уравнений вытекает следующее правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах ( Σ h). Пример такого построения дан на рис. 6.3, б.

Разветвленное соединение. Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение — место разветвления (или смыкания) труб.

Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три трубы1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рис. 6.5, а). Геометрические высоты z₁, z₂ и z₃ конечных сечений и давления P₁, P₂ и P₃ в них будут также различны.

Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме расходов в каждом трубопроводе:

Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода, получим (пренебрегая разностью скоростных высот)

Обозначив сумму первых двух членов через H_ст и выражая третий член через расход (как это делалось в п.6.1), получаем

Аналогично для двух других трубопроводов можно записать

Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q₁, Q₂ и Q₃ и H_M.

Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) — сложением абсцисс (Q) при одинаковых ординатах (H_M). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3 , а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство H_M > H_ст1.

Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).

Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б). магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q _B и Q_D и Q_E .

Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M — N и избыточные давления в конечных точках P_B и P_D и P_E.

Для этого случая возможны два вида задач:

Задача 1. Дан расход Q в основной магистрали M_A. Необходимо определить расходы Q_B и Q_D и Q_E, а также потребный напор в точке М.

Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви.

Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно:

уравнение равенства потребных напоров для ветвей CD и CE

уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD

выражение для потребного напора в точке М

Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом:
1) сложный трубопровод разбивают на ряд простых;
2) строят кривые потребных напоров для каждого из простых трубопроводов;
3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов;
4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу (см. п.6.2).

Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости.

Сложный кольцевой трубопровод. Представляет собой систему смежных замкнутых контуров, с отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках (рис. 6.7).

Задачи для таких трубопроводов решают аналогичным методом с применением электроаналогий (закон Кирхгофа). При этом основываются на двух обязательных условиях. Первое условие — баланс расходов, т.е. равенство притока и оттока жидкости для каждой узловой точки. Второе условие — баланс напоров, т.е. равенство нулю алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой стрелки или против нее.

Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и длины семи участков. Требуется определить диаметры трубопроводов на всех участках.

Как уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, может создаваться работой насоса, что широко применяется в машиностроении. Рассмотрим совместную работу трубопровода с насосом и принцип расчета трубопровода с насосной подачей жидкости.

Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость перекачивается из одной емкости в другую (рис. 6.8, а), или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости (рис. 6.8, б).

Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P ₀ в другой резервуар с давлением P₃ (рис. 6.8, а). Высота расположения оси насоса H₁ называетсягеометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу,всасывающим трубопроводом или линией всасывания. Высота расположения конечного сечения трубопровода H₂ называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией нагнетания.

Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1 (принимая α = 1):

Это уравнение является основным для расчета всасывающих трубопроводов.

Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений 2-2и 3-3:

Левая часть этого уравнения представляет собой энергию жидкости на выходе из насоса. А на входе насоса энергию жидкости можно будет аналогично выразить из уравнения:

Таким образом, можно подсчитать приращение энергии жидкости, проходящей через насос. Эта энергия сообщается жидкости насосом и поэтому обозначается обычно H_нас.

Для нахождения напора H_нас вычислим уравнение :

где Δz — полная геометрическая высота подъема жидкости, Δz = H ₁ + H₂;
КQ m — сумма гидравлических потерь,
P₃ и Р₀ — давление в верхней и нижней емкости соответственно.

Если к действительной разности уровней Δz добавить разность пьезометрических высот ( P₃ — Р₀ ) ( ρg ), то можно рассматривать увеличенную разность уровней

и формулу можно переписать так:

Из этой формулы делаем вывод, что

Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному.

На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в совместном построении в одном и том же масштабе и на одном графике двух кривых: напора H_потр = f₁(Q)и характеристики насоса H_нас = f₂(Q) и в нахождении их точки пересечения (рис. 6.9).

Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса. На рис. 6.9 дано два варианта графика: а — для турбулентного режима; б — для ламинарного режима. Точка пересечения кривой потребного напора с характеристикой насоса называется рабочей точкой. Чтобы получить другую рабочую точку, необходимо изменить открытие регулировочного крана (изменить характеристику трубопровода) или изменить частоту вращения вала насоса.

Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или другого устройства, управляемого потоком.

Пусть в конце трубы, по которой движется жидкость со скоростью υ₀, произведено мгновенное закрытие крана (рис. 6.10, а).

При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в соответствии с увеличением давления на величину ΔP_уд, которое называется ударным. Область (сечение n — n), в которой происходит увеличение давления, называется ударной волной. Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны.

Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы — растянутыми. Ударное повышение давления распространится на всю длину трубы (рис. 6.10, б).

Далее под действием перепада давления ΔP_уд частицы жидкости устремятся из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-nперемещается обратно к крану с той же скоростью c, оставляя за собой выровненное давление P₀ (рис. 6.10, в).

Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующему давлению P₀. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость υ₀, но направленную теперь в противоположную теперь сторону.

С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная ударная волна под давлением P₀ — ΔP_уд, которая направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления (рис. 6.10, д). Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака.

Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис. 6.10, е. Так же как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рис. 6.10, ж, показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью υ₀.

Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP _уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится.

Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 6.11, а и б.

Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной действительный вид картины изменения давления по времени (рис. 6.11, а). При этом затухание колебаний давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар.

Повышение давления при гидравлическом ударе можно определить по формуле

Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c определится по формуле:

где r — радиус трубопровода;
E — модуль упругости материала трубы;
δ — толщина стенки трубопровода;
K — объемный модуль упругости (см. п.1.3)

Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E = , то скорость ударной волны определится из выражения

Для воды эта скорость равна 1435 м/с, для бензина 1116 м/с, для масла 1200 — 1400 м/с.

При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период эксплуатации снижается (например, для водопроводных труб до 50% и даже ниже). Вследствие коррозии и образования отложений в трубах (инкрустации), шероховатость труб увеличивается. Это можно оценить по формуле:

где k₀ — абсолютная шероховатость для новых труб, (мм),
k_t — шероховатость через t лет эксплуатации,
α — коэффициент характеризующий быстроту возрастания шероховатости (мм/год).

Расчёт коротких трубопроводов

РАСЧЁТ ТРУБОПРОВОДОВ

к расчётной работе по дисциплине «Гидрогазодинамика»

Составитель А.В. Севостьянов

Липецкий государственный технический университет

Рецензент Е.М. Крамченков

Севостьянов, А.В.

С 281 Расчёт трубопроводов [Текст]: методические указания к расчётной работе по дисциплине «Гидрогазодинамика» / А.В. Севостьянов. – Липецк: Изд-во ЛГТУ, 2014. – 47 с.

В методических указаниях приводится алгоритм расчёта коротких и длинных трубопроводов, описан подбор насоса для выбранных рабочих параметров длинного трубопровода.

Методические указания предназначены для студентов I курса специальности «Промышленная теплоэнергетика».

Табл. 3. Ил. 28. Библиогр.: 3 назв.

© ФГБОУ ВПО «Липецкий государственный технический университет», 2014

1. Расчёт коротких трубопроводов. 8

2. Расчёт длинных трубопроводов. 10

3. Построение графика пьезометрической линии. 12

4. Подбор насоса для сети. 13

5.1. Варианты задания на расчёт короткого трубопровода. 15

5.2. Варианты задания на расчёт короткого трубопровода. 34

6. Пример решения – расчёт короткого трубопровода. 35

6.2. Определение объёмного расхода. 36

6.3. Определение показания манометра 38

6.4. Определение напора насоса. 40

7. Пример решения – расчёт длинного трубопровода. 41

7.1. Расчёт магистрали. 41

7.2. Расчёт ответвления. 43

7.3. Построение графика пьезометрической линии. 45

7.4. Подбор насоса. 46

Библиографический список. 47

Перечень условных обозначений

d – диаметр трубопровода, м;

d_н – наружный диаметр трубопровода, м;

g = 9,81 м/с 2 — ускорение силы тяжести;

h – высота жидкости в колене жидкостного манометра, м;

h_вс – высота всасывания насоса, м;

h_1-2 – потери напора между сечениями 1 и 2, м;

h_w – потери напора на вязкое трение, м;

h_м.с. – потери напора на местном сопротивлении, м;

l – длина трубопровода, м;

р₀ – давление на поверхности жидкости, Па;

s – толщина стенки трубы, м;

t – температура, °С;

z – геометрическая высота, м;

D_у – условный диаметр трубопровода, м;

D_к – диаметр рабочего колеса насоса, м;

H – высота, пьезометрический напор, м;

K — сопротивление трубопровода, с 2 /м 5 ;

Re – критерий Рейнольдса;

– объёмный расход, м 3 /с;

— потребный расход, м 3 /с;

— коэффициент местного сопротивления;

— коэффициент местного сопротивления поворота;

— коэффициент трения;

— коэффициент кинематической вязкости, м 2 /с;

— коэффициент кинематической вязкости для заданной температуры, м 2 /с;

— коэффициент кинематической вязкости для t = 50 °C, м 2 /с;

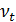
Δ_э – эквивалентная шероховатость, м;

Δh — удельный перепад напора, м/м;

ΔH — перепад напора, м;

Δz – перепад геометрических высот, м.

Обозначения на схемах

(1) и (2) – первое и второе приближения;

Введение

Основными результатами расчёта трубопроводов являются сводка диаметров труб на всех участках и потери напора или давления от источника до диктующей точки. Диктующей точкой называется место расположения потребителя, который находится в самом невыгодном положении по сравнению с другими потребителями. Если потребитель в критической точке получает необходимый расход при заданном напоре, то снабжение остальных потребителей не вызывает проблем. Потери напора в сети наряду с потребным расходом являются основными параметрами, определяющими выбор насоса.

Основой гидравлического расчёта трубопроводов является уравнение Бернулли [1]. Для несжимаемой среды уравнение имеет следующий вид

. (1)

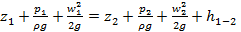
Важным моментом является выбор положения плоскости сравнения 0-0, от которой производится отсчёт геометрических высот z₁ и z₂ для двух живых сечений, в которых определяются необходимые параметры.

Потери напора h_1-2 между выбранными живыми сечениями являются суперпозицией потерь на вязкое трение в жидкости и потерь на местных сопротивлениях. Потери на вязкое трение определяются по формуле Д’Арси

(2)

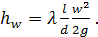
Коэффициент трения в этом соотношении зависит от режима течения и области сопротивления. Режим течения можно установить по значению критерия Рейнольдса. Значение критерия Рейнольдса определяется характерными параметрами: средней по живому сечению скоростью, внутренним диаметром трубы и коэффициентом кинематической вязкости жидкости для заданной температуры

. (3)

Коэффициент кинематической вязкости сильно зависит от температуры. Для воды используется эмпирическая формула

. (4)

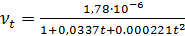
Для минеральных масел применяется формула

, (5)

для солярового масла ν₅₀=7·10 -6 м 2 /с, n=1.54.

Если Re 2300) выбор формулы для коэффициента трения зависит от области сопротивления. Границы области определяются с помощью комплекса 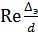. Для области гидравлически гладкой трубы

, (7)

для переходной (доквадратичной) области

(8)

и для области гидравлически шероховатой трубы (квадратичной области)

. (9)

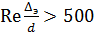
Для каждой области сопротивления предлагаются свои соотношения для коэффициента трения. Наиболее популярными является степенные формулы:

для гидравлически гладких труб – формула Блазиуса

, (10)

для переходной области – формула Альтшуля

, (11)

для гидравлически шероховатых труб – формула Шифринсона

. (12)

Степенные формулы справедливы в диапазоне значений Re 5 . Для значений Re > 10 5 формулы (8) – (10) дают заметную ошибку, поэтому в этом диапазоне значений Re используются логарифмические формулы:

для гидравлически гладких труб – формула Конакова

, (13)

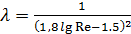
для гидравлически шероховатых труб – формула Никурадзе

. (14)

Для переходной области применяется формула Коулбрука и Уайта

. (15)

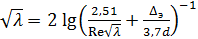
Уравнение (15) является трансцендентным и по этой причине непопулярным. Таблицы и графики, основанные на этом уравнении, можно найти в справочниках [2].

Потери на местных сопротивлениях определяются по формуле Вейсбаха

. (16)

По умолчанию в уравнение (14) входит скорость за сопротивлением. Коэффициенты местных сопротивлений в диапазоне значений Re > 1000 определяются только формой местного сопротивления и их значения для наиболее часто встречающихся местных сопротивлений приводятся в справочниках [2].

Для несжимаемых жидкостей одним из параметров потока является объёмный расход

, (17)

для потока в круглой цилиндрической трубе

. (18)

Расчёт коротких трубопроводов

Короткими называются трубопроводы, в которых потери напора на вязкое трение и на местных сопротивлениях сопоставимы по величине.

Существует несколько типов задач, встречающихся при расчёте коротких трубопроводов. Задача в прямой постановке (конструктивный расчёт) предполагает задание потребных расходов и плана трубопровода с геометрическими отметками узловых точек. В этом случае определяются диаметры труб на каждом участке и суммарные потери. Проверочный расчёт предполагает известными диаметры всех участков трубопровода. Целью проверочного расчёта является определение пропускной способности трубопровода, т.е. определение расходов при заданном напоре или определение потребного напора при заданных расходах.

Для определения общих потерь в трубопроводе используется принцип суперпозиции (наложения) потерь

. (19)

Уравнение (17) выписано для трубопровода, содержащего n участков и m местных сопротивлений и справедливо для случаев, когда расстояние между местными сопротивлениями не менее 20 50 калибров (диаметров трубы).

Основным расчетным соотношением для коротких трубопроводов является уравнение Бернулли (1). Для успешного применения уравнения (1) необходимо выполнить следующую последовательность действий:

а) выбрать положение плоскости сравнения. Строгих требований по выбору плоскости сравнения нет, рекомендуется размещать её наиболее удобным для последующего решения образом;

б) выбрать два живых сечения потока. Наиболее удачным считается такое расположение живых сечений, при котором в этих сечениях сосредотачивается большая часть известных параметров и неизвестный параметр. Не всегда удаётся выбрать живые сечения с первого раза, иногда приходится возвращаться к этому пункту и корректировать положение этих сечений;

в) рекомендуется выписать уравнение Бернулли в виде, наиболее удобном для последующего решения. Для несжимаемых жидкостей – это уравнение (1);

г) необходимо идентифицировать параметры уравнения (1) с исходными данными;

д) выписать уравнение Бернулли с максимальным использованием исходных данных;

е) разрешить полученное уравнение относительного неизвестного. Может случиться так, что в полученном уравнении окажутся два или более неизвестных. В этом ситуации необходимо привлекать так называемые замыкающие уравнения. Самым популярным из них является уравнение баланса расходов

, (20)

которое позволяет выразить скорость в одном сечении через скорость в другом.

При решении сложных задач очень полезным может быть приём, называемый декомпозицией, т.е. разложение сложной задачи на последовательность более простых, что сильно облегчает решение поставленной задачи. В таких ситуациях приходится применять уравнение (1) несколько раз.

Расчет простого гидравлически короткого трубопровода

Рассмотрим расчет простого гидравлически короткого трубопровода. При этом используем уравнение Бернулли и другие уравнения, приведенные выше.

Расчет начинается с составления уравнения Бернулли для расчетной схемы, при этом придерживаются следующей методики.

1. Выбирают положение плоскости сравнения.

Обязательным требованием при выборе положения плоскости сравнения является ее горизонтальность, т.е., она должна быть перпендикулярна линии действия сил тяжести. Для упрощения расчетов и исключения возможных ошибок при определении геометрических напоров, плоскость сравнения 0-0 выбирают таким образом, чтобы . Но иногда целесообразно выбирать и другие положения плоскости сравнения, например, вдоль оси горизонтальной части трубопровода. Пример выбора плоскости сравнения приведен на рисунке 45.

Рисунок 45 — Схемы трубопроводов

2. Выбирают расчетные сечения.

Часто уравнение Бернулли применяется для определения разности пьезометрических напоров, под действием которых жидкость с заданным расходом Q движется в напорных трубопроводных системах. Если же напор известен, то по уравнению определяют расход жидкости или необходимый диаметр трубопровода. Для сокращения числа неизвестных величин, входящих в уравнение Бернулли, целесообразно сечения 1-1 и 2-2 выбирать таким образом, чтобы наибольшее количество членов уравнения было известно, или же легко определялось. Величины давлений выбирают как в абсолютных, так и в относительных значениях, но в идентичных значениях для обоих сечений. Если в сечении 1-1 выбрана величина избыточного давления, то и в сечении 2-2 тоже должно быть указано избыточное давление. В тех случаях, когда в одном из сечений давление равно атмосферному, давление удобнее выбирать в избыточных значениях.

3. Конкретизируют уравнение Бернулли для конкретной расчетной схемы трубопровода. Т.е. подставляют известные величины в уравнения и выясняют неизвестные.

Для лучшего понимания рассмотрим пример составления уравнения Бернулли для трубопровода, представленного на рисунке 46. Выбираем плоскость сравнения 0-0 таким образом, что все сечения напорной системы лежат выше этой плоскости, а центр тяжести выходного сечения трубопровода совпадает с ней. Выбираем расчетные сечения:

1-1 — по свободной поверхности жидкости в напорном резервуаре, 2-2 — на выходе из трубопровода.

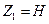
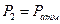
В сечениях 1-1 и 2-2 известны следующие величины (см. рис.46): , , , (так как приток и отток из резервуара равны между собой), , , .

Рисунок 46 — Расчетная схема трубопровода

Таким образом, после подстановки указанных величин в исходное уравнение, получим конечный вид уравнения Бернулли для случая, представленного на рисунке 46:

.

В уравнении пока неизвестны скоростной напор в конечном сечении и потери напора в трубопроводе ( ; ).

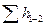
Определение потерь напора будет рассмотрено ниже, а скоростной напор определяется с использованием уравнения неразрывности. Из уравнений неразрывности следует, что скорости обратно пропорциональны площадям живых сечений:

Тогда по известному расходу можно найти значение скорости в конечном сечении и скоростной напор .

4. Определяют потери напора 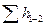. Отметим, что расчет потерь связан с выявлением характерных гидравлических сопротивлений. Потери напора слагаются из потерь двух видов:

— потерь напора на преодоление гидравлических сопротивлений по длине, пропорциональных длине участков русла или трубы, по которым движется жидкость, т.е. потерь на трение ;

— потерь напора на преодоление гидравлических сопротивлений в пределах коротких участков в непосредственной близости к тем или иным местным конструктивным устройствам (вход, выход, расширение, сужение, поворот, трубопроводная арматура, фасонина и т.п.), т.е. местных потерь напора .

Принимается, что общие потери напора в системе равны сумме потерь напора по длине отдельных участков и всех местных потерь напора:

.

Для расчета потерь по длине (на трение) и местных потерь пользуются формулами Дарси-Вейсбаха и Вейсбаха:

, .

После того, как получен окончательный вид уравнения Бернулли и выявлены все возможные потери напора, определяют тип задачи, которую необходимо решить:

• Определение перепада напора Н (потребного напора), необходимого для пропуска заданного расхода жидкости по заданному трубопроводу (с известными длинами и диаметрами).

Эту задачу можно решить аналитически достаточно просто, используя конечный вид уравнения Бернулли для системы, подставив в него все известные величины, рассчитав потери напора.

• Определение расхода жидкости, который может пропустить заданный трубопровод с известным диаметром, длиной и перепадом давлений в начальном и конечном сечении (известной потерей напора).

Задачу этого типа решить аналитически достаточно трудно, т.к. скорость V и коэффициент Дарси зависит от расхода Q, который в начале расчета неизвестен.

При решении задачи используют или метод последовательных приближений (итерации) или графо-аналитический метод. При этом задаются рядом значений расхода Q и добиваются равенства левой и правой частей уравнения Бернулли. При использовании метода итерации получается большой объем вычислений. При использовании графо-аналитического метода достаточно трех-четырех приближений, после чего строится график зависимости Σh_1-2=f(Q) и по нему определяется искомый расход. Пример построения зависимости Σh_1-2=f(Q) показан на рисунке 47.

Рисунок 47 — Графо-аналитический метод

Определение необходимого диаметра трубопровода, обеспечивающего пропуск известного расхода при заданных длине и перепаде напоров (давлений).

Как и в предыдущем случае используются методы последовательного приближения или графо-аналитический, но задаются несколькими значениями диаметра и по результатам расчета строят график зависимости (d), по нему и подбирают искомый диаметр.

Пример решения этой задачи графо-аналитическим методом приведен на рисунке 48.

Рисунок 48 — Применение графо-аналитического метода.

5. Следующим пунктом расчета является построение напорной и пьезометрической линий.

После того, как решением уравнения Бернулли установлены напоры в начальном и конечном сечениях, расход и потери напора, можно приступить к построению напорной линии.

Построение напорной линии начинается с исходного сечения 1-1. Определяем для него гидродинамический напор с учетом того, что , а следовательно, . Если бы на пути от сечения 1-1 до сечения 6-6 не было бы сопротивлений, то потери напора не происходило бы и напорная линия оказалась бы параллельной плоскости сравнения 0-0, исходя из сечения 1-1. Гидравлические сопротивления, возникающие в реальной жидкости, будут приводить к уменьшению исходного напора на величину потерь на трение и местные сопротивления. При построении напорной линии эти потери откладываются вниз от исходного значения напора.

Потеря на вход на участке 1-2 понизит напорную линию на величину h_м, на трение на участке 2-3 на величину h_тр, и т.д. (см. рис.49). В итоге мы получим ломаную линию, показывающую изменение напора при движении жидкости из сечения 1-1 в сечение 6-6. Интенсивность потерь напора (энергии) называется гидравлическим уклоном, который равен отношению потерь напора на трение по длине h_тр, к длине участка l_i.

Пьезометрическую линию строят следующим образом:

— определяют скоростной напор на каждом участке постоянного диаметра;

— откладывают вниз от напорной линии соответствующие значения величин скоростного напора

Получаем ломаную линию, называемую пьезометрической линией. Как видно пьезометрическая линия на участке проходит параллельно и ниже напорной на величину скоростного напора на участке. На участках, где происходит изменение диаметров трубопровода, параллельность нарушается из-за различия скоростных напоров α_iV_i/2g и α_i+1 V_i+1/2g.

Рисунок 49 — Пример построения пьезометрической и напорной линий.