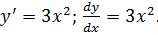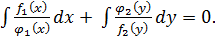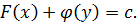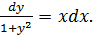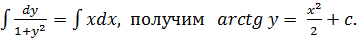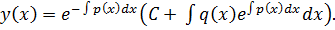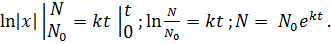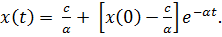Применение дифференциальных уравнений первого порядка для решения задач
Раздел 1. Математический анализ
Тема 1.4. Дифференциальные уравнения и их применения в медицине
1. Основные понятия и определения дифференциального уравнения.
2. Методы решения некоторых дифференциальных уравнений.
3. Применение дифференциальных уравнений первого порядка для решения задач.
Основные понятия и определения дифференциального уравнения
Опр. Равенство, связывающее независимую переменную х, неизвестную функцию у = f(x), а так же её производные y’,y”,….. y n , называется обыкновенным дифференциальным уравнением.
F(x,y.y’,y”………) = 0, где F – известная функция, заданная в некоторой фиксированной области; х – независимая переменная; у – зависимая переменная; y’,y”,….. y n – её производные.
Опр. Решением дифференциального уравнения называется функция у = f(x), которая будучи представлена в уравнении F(x,y.y’,y”………) = 0, обращает его в тождество. График этой функции называется интегральной кривой.
Пример 1.1. Дифференциальное уравнение
Представим в виде: 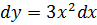
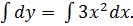
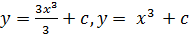
Методы решения некоторых дифференциальных уравнений
Выбор метода решения дифференциального уравнения зависит от его вида.
Дифференциальные уравнения первого порядка с разделяющимися переменными.
Уравнения вида 
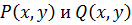
После резделения переменных, когда каждый член будет зависеть только от одной переменной, общий интеграл уравнения находится почленным интегрированием:
Решением этого уравнения будет:
Пример 2.1. Найти решение уравнения: 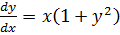
Разделим уравнение на множители, зависящие только от одной переменной:
Проинтегрируем левую и правую части:
Общее решение:
Линейные дифференциальные уравнения первого порядка.
Опр. Уравнения вида: 
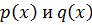
При 

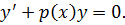
При 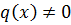

Применение дифференциальных уравнений первого порядка для решения задач
Этапы решения задач с помощью дифференциальных уравнений:
1. Оформить условия, в которых протекают изучаемые процессы;
2. Выбрать зависимые и независимые переменные;
3. Определить функциональные зависимости между ними
4. Решение уравнения;
5. Анализ полученных решений.
В уравнениях, описывающих медико-биологические процессы, в качестве независимой переменной чаще всего используется временная компонента.
Размножение бактерий
Если бактерии обитают в благоприятной среде, то скорость размножения бактерий пропорциональна размеру популяции. Такое предположение описывается дифференциальным уравнением: 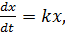


Вычислим определённые интегралы:
Получим экспоненциальную кривую, которая зависит от времени и k. Если 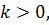
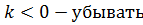
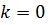
| N |
| N0 |
| k 0 |
| t |
Для определения значения k необходимо иметь дополнительные сведения об изменении численности бактерий за определённый промежуток времени.
Внутривенное введение глюкозы
При внутривенном введении с помощью капельницы скорость поступления глюкозы в кровь постоянна и равна с. В крови глюкоза разлагается и удаляется из кровеносной системы со скоростью, пропорциональной имеющемуся количеству глюкозы. Тогда дифференциальное уравнение, описывающее этот процесс, имеет вид: 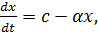
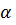
Это неоднородное линейное дифференциальное уравнение первого порядка, и его общее решение находиться по формуле:

Тогда 
Частное решение уравнения 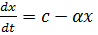
При увеличении времени уровень глюкозы в крови приближается к 
ГЛАВА 3. Применение дифференциальных уравнений первого порядка для решения прикладных задач физики, биологии, медицины
Задача 1. Скорость размножения некоторых бактерий пропорциональна количеству бактерий, имеющихся в наличии в рассматриваемый момент времени t. Количество бактерий утроилось в течение 5 часов. Найти зависимость числа бактерий от времени.
Решение. Обозначим количество бактерий в момент времени t через x, тогда 
По условию задачи 
Потенцируем последнее выражение и получаем общее решение нашего дифференциального уравнения.
Найдем частное решение, соответствующее начальным условиям
При t=0, x=x0 
Чтобы найти искомую зависимость, определим коэффициент пропорциональности k. По условию задачи известно, что через 5 часов 
Прологарифмируем последнее выражение
Окончательно получаем
Задача 2. При прохождении света через вещество происходит ослабление интенсивности светового потока, вследствие превращения световой энергии в другие виды энергии, т.е. происходит поглощение света веществом. Найти закон поглощения, если известно, что ослабление интенсивности пропорционально толщине слоя и интенсивности падающего излучения.
Решение. Исходя из условия задачи, можно сразу написать дифференциальное уравнение

где dI -ослабление интенсивности при прохождении слоя толщиной dx.
k -коэффициент пропорциональности.
Знак минус показывает, что интенсивность падает по мере прохождения слоя.
Проинтегрируем наше уравнение, предварительно разделив переменные
Исходя из того, что падающий на поверхность вещества свет имел интенсивность I=I0 , при x=0, найдем частное решение
Итак, мы получили закон поглощения света веществом ( закон Бугера), где
k -натуральный показатель поглощения.
Задача 3. Известно, что механические свойства биологических объектов изучаются с помощью вязкоупругих моделей (поршень — пружина). Одной из найболее распространенных является модель Кельвина — Фойхта, состоящая из параллельно соединенных пружины и поршня (см. рис.1).
Рис. 4. Модель Кельвина — Фойхта
Найти зависимость деформации от времени 
Решение. Согласно условию задачи 



Проинтегрируем полученное дифференциальное уравнение от начального момента времени и нулевой деформации до текущих значений t и 
Потенцируя последнее выражение, получаем
Находим отсюда
Как видно из полученной формулы, в рамках модели Кельвина — Фойхта деформация при постоянной нагрузке возрастает с течением времени. Это соответствует реальным материалам. Такое свойство материала названо текучестью.
Интегрированный урок по математике и информатике “Применение дифференциальных уравнений при решении прикладных задач различных предметных областей, их анализ и графическая интерпретация”.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Муниципальное бюджетное общеобразовательное учреждение – гимназия №19
Интегрированный урок по математике и информатике
“ Применение дифференциальных уравнений
при решении прикладных задач
различных предметных областей,
их анализ и графическая интерпретация”.
Подготовили и провели:
Тюпин Владимир Владимирович;
учитель информатики и ИКТ
Кривоногов Константин Юрьевич.
2013-2014 учебный год
Тема урока: “Применение дифференциальных уравнений при решении прикладных задач различных предметных областей, их анализ и графическая интерпретация”.
1. Обобщение теоретического материала по теме «Неопределенный интеграл и дифференциальные уравнения».
2. Обобщение теоретического материала по теме «Прикладные среды и системы программирования для решения математических задач».
3. Исследовательская работа в группах.
4. Представление аналитического и графического решений поставленных задач.
5. Анализ результатов и выводы.
Цели и задачи урока.
1. Обобщение теоретического материала по темам: «Неопределенный интеграл и дифференциальные уравнения», «Прикладные среды и системы программирования для решения математических задач».
2. Отработка навыков решения дифференциальных уравнений аналитическим и графическим способами на основе прикладных задач предметов естественнонаучного цикла.
3. На основе полученных результатов сделать вывод о применении различных средств и методов математики и информатики к решению задач физики, химии, экологии.
Перед тем как вы начнете выполнять исследовательскую работу мы с вами должны повторить основные понятия и методы решения задач, непосредственно связанных с темой нашего урока.
1. Давайте вспомним как называется раздел математики, который мы сейчас изучаем.
2. Что называется интегральным исчислением?
Давайте вспомним базовые понятия интегрального исчисления.
3. Дайте определение первообразной функции f ( x ).
4. Что называется интегралом функции f ( x )?
Непосредственная ваша работа на уроке будет связана с решением дифференциальных уравнений. Так давайте же вспомним основные понятия связанные с ними.
5. Какое уравнение называют дифференциальным?
6. Что называется решением дифференциального уравнения?
7. Что значит решить задачу Коши для дифференциального уравнения?
Есть такое понятие связанное с дифференциальным уравнением, как порядок.
8. Что называют порядком дифференциального уравнения?
На доске представлены различные виды дифференциальных уравнений.
9. Назовите их и дайте соответствующие определения.
На доске представлены также различные виды решений линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
10. От каких условий зависит появление того или иного решения данного дифференциального уравнения?
11. Что позволяет найти характеристическое уравнение?
Итак, повторив основные вопросы математики вам предстоит аналогичная работа и по информатике.
Повторив основные понятия по математике и информатики, относящиеся к теме нашего сегодняшнего урока у вас есть прекрасная возможность применить полученные знания на практике в процессе решения предложенных вам исследовательских задач.
На столе у каждой лаборатории лежат листочки с исследовательскими задачами. Каждой лаборатории предстоит сначала получить функциональную зависимость описывающую тот или иной процесс, составив и решив дифференциальное уравнение, а затем данное решение реализовать графически в среде Excel и Delphi . Это вам поможет сделать справочный материал по данной тематике так же находящийся у вас на столе.
Далее один представитель каждой лаборатории представляет нам математическую часть решения задачи на доске, а два других её графическую интерпретацию на экране.
На данном уроке мы с вами обобщили теоретический материал по темам «Неопределённый интеграл, дифференциальные уравнения» и «Прикладные среды и системы программирования для решения задач».
После чего успешно мы с вами увидели применение данного материала на практике при решении прикладных задач предметов естественнонаучного цикла.
На столах для каждого лежат листочки с домашним заданием, в котором вам предлагается решить прикладную задачу геометрического содержания способами, рассмотренными нами на уроке
Составьте уравнение кривой, для которой отрезок касательной между точками касания и осью ординат делится пополам в точке пересечения с осью абсцисс. Каковы начальные условия, если кривая проходит через точку А (1;3). Представить графическую интерпретацию решения данной задачи в прикладной среде и среде программирования.
Подводя итоги работы, можно сказать, что все учащиеся с заданием справились успешно и получают следующие отметки:
http://megaobuchalka.ru/9/21993.html
http://infourok.ru/integrirovannyy_urok_po_matematike_i_informatike______primenenie_differencialnyh_uravneniy_pri-489131.htm